计及保护失效的输电网可靠性评估

张占龙，么 莉，雷林绪，林济铿，魏文辉，韩佳兵（.天津大学电气与自动化工程学院，天津 0007；.国网智能电网研究院，北京 000；.同济大学电子与信息工程学院，上海 080；.北京科东电力控制系统有限责任公司，北京 00085）

计及保护失效的输电网可靠性评估

张占龙1，么 莉1，雷林绪2，林济铿3，魏文辉4，韩佳兵4
（1.天津大学电气与自动化工程学院，天津 300072；2.国网智能电网研究院，北京 102200；3.同济大学电子与信息工程学院，上海 201804；4.北京科东电力控制系统有限责任公司，北京 100085）

如何提高输电系统可靠性分析的准确性一直是电力系统可靠性分析的热点课题。基于对保护两类失效、断路器失效及保护系统之间的配合对线路停运的影响分析，首先提出了结合线路完整模型及序贯蒙特卡洛仿真的输电系统可靠性分析新方法；然后建立了可计及保护、断路器失效影响的输电线路完整Markov模型；再根据该模型，采用序贯蒙特卡洛方法，对包括一次和二次设备的电力系统状态进行抽样仿真，并计算出各类可靠性指标，实现了完整电力系统的可靠性分析。所建线路状态模型完整，符合实际的运行状况，从而使得基于所提模型得到的系统可靠性分析结果的准确性及可信性更高。算例证明了所提方法的有效性。

可靠性评估；保护失效；断路器拒动；序贯蒙特卡洛仿真；Markov模型

继电保护作为电力系统二次设备中的重要元件之一，其正确动作与否将直接影响电力系统运行的安全性及可靠性。近年来由继电保护失效引起的电力系统故障越来越突出［1-3］，科学合理地计及继电保护系统对一次设备及系统安全运行的影响，对提高大电网可靠性分析结果可信度及准确度是一个非常关键的问题。

当前计及继电保护影响的系统可靠性分析，根据其可靠性模型的建立过程大致可分成2类。第1类是以影响因子累加的方式计及保护系统对于一次设备失效率的影响。文献［4］在对继电保护硬件失效和原理性失效分别进行概率分析的基础上，结合实时潮流、天气等因素对设备停运的影响，以影响因子累加的方式为输电线路、变压器等输电系统主要设备建立了运行可靠性模型；文献［5-6］分析了计及保护失效影响的输电线路的4种停电模式，并基于此将保护的拒误动失效率累加到线路自身的停运率之中；文献［7］结合继电保护配置方案及拒误动两种失效模式，建立了继电保护对一次设备可靠性影响的Markov模型，并将保护对一次设备的影响定量描述为保护可靠性对一次设备不可用度的贡献量。上述文献均将保护失效影响以影响因子的方式直接添加到被保护元件的停运率或不可用概率之中，由于没有详细考虑保护系统配置、配合以及断路器失效等因素的影响，因此其可靠性分析结果的准确性相对较低。第2类是建立一次设备及二次保护系统的联合可靠性分析模型来计及保护系统对于电力系统运行可靠性影响。文献［8］综合事件树与故障树的分析方法，定量分析了保护故障对系统供电可靠性的影响，其实质上是利用状态枚举法进行保护系统和一次系统的联合可靠性进行分析，随着系统规模的增大其计算量将急剧增加；文献［9］基于保护拒误动2种典型的失效模式及相邻继电保护系统之间的协调配合关系，建立了输电线路的12状态Markov分析模型，并分别用马尔可夫状态空间法和蒙特卡洛方法对简单及复杂系统的可靠性进行了评估。该方法可同时适用于简单系统及实际大系统，是一有效实用方法，但该方法在保护可靠性建模过程中只考虑了保护范围内无故障发生时的误动失效模式，而没有考虑更为常见的非选择性误动失效［4］，即在被保护设备的相邻下一级设备发生短路等故障的前提下，由继电保护装置的运行环境参数（电网运行方式、保护整定值等）导致的非选择性跳闸。此外，该文没有考虑保护装置执行机构-断路器的失效，而根据实际运行经验和电力系统故障的相关统计分析［10-11］，断路器的失效概率与二次保护系统的失效概率为同一数量级，若不计断路器故障的影响，将会使得可靠性分析结果过于乐观。

基于此，本文提出了一种基于线路完整模型及序贯蒙特卡洛仿真的输电系统可靠性分析新方法。结合保护拒误动、断路器失效及保护系统之间的配合对线路停运的影响，本文建立了可计及保护、断路器失效影响的输电线路完整Markov状态分析模型。然后基于此模型，采用序贯蒙特卡洛方法，对包括一、二次设备的电力系统状态进行抽样仿真，并计算各类可靠性指标，从而实现了完整电力系统的可靠性分析。

1 保护失效影响及线路停电模式分析

继电保护不可靠运行时将导致其不能有选择性且快速地切除保护区域内的故障元件，运行失效方式一般可分为保护拒动和误动2种［12］。保护拒动是指保护装置因不能正确检测出区内故障而发出跳闸信号，使得故障元件不能被及时切除。保护发生拒动失效时需要由后备保护来切除故障元件，从而造成停电范围扩大以及故障切除时间延长［13］。保护误动包括2种情况：①被保护范围内未发生故障而保护错误发出跳闸信号使得断路器断开被保护设备；②设备发生故障时其主保护及近后备未拒动，该设备的远后备保护发生非选择性越级误动导致停电范围扩大。保护误动会增加被保护设备的停运概率。

保护系统中的断路器作为保护装置的执行机构，其拒动时也会造成故障元件不能及时断开，需要该元件的后备保护动作切除故障元件，从而引起其他正常元件的停运。

根据对继电保护和断路器的失效影响分析，计及保护及断路器失效影响的一次设备（以输电线路为分析对象，其他类似）有4种停运类型：①线路本身发生故障而被保护及断路器正确动作而切除；②相邻线路发生故障且其保护装置或断路器拒动，本线路的保护作为其远后备保护动作，导致未发生故障的本线路也被切除而停电；③线路未发生故障，其保护发生误动而被切除导致停电，或称一次设备正常运行而因保护系统的误动而被切除；④相邻线路发生故障且其保护与断路器未拒动，本线路保护作为其远后备保护发生非选择性误动将未发生故障的本线路断开，或称因保护发生非选择性误动导致线路被切除。

基于上述4种停运模式，本文建立了计及保护和断路器失效影响的输电线路完整Markov状态分析模型，以便计算计及保护系统的电力系统可靠性指标。

2 输电线路的完整Markov状态分析模型

以图1简单系统为例进行建模分析。为了分析断路器拒动失效的影响，本文将断路器和保护装置分开考虑。图中，A、B为两条线路，分别配备主保护装置RA1、RA2、RB1和RB2，A1、A2为线路A两端的断路器，B1、B2为线路B两端的断路器，S1、S2为发电机，L为负荷。其中A、B的主保护均作为对方的后备保护，S1、S2的保护也分别作为A 和B的后备保护，本文只考虑远后备保护，且认为远后备保护100%可靠。本文以图中的输电线路A为例进行建模分析。

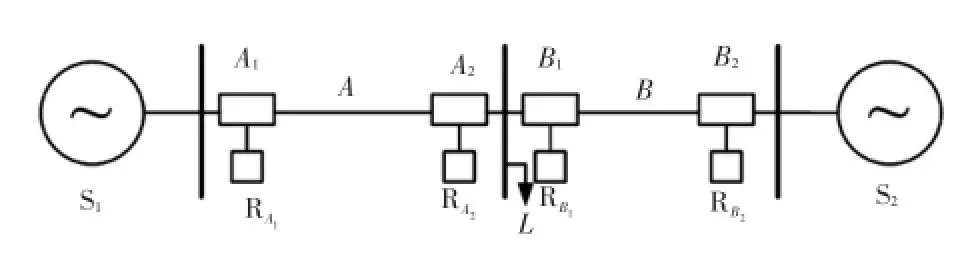
图1 示例电力系统Fig.1 Example power system

根据计及不同保护失效模式及断路器拒动影响的输电线路4种停电类型，本文建立了如图2所示的Markov状态模型。

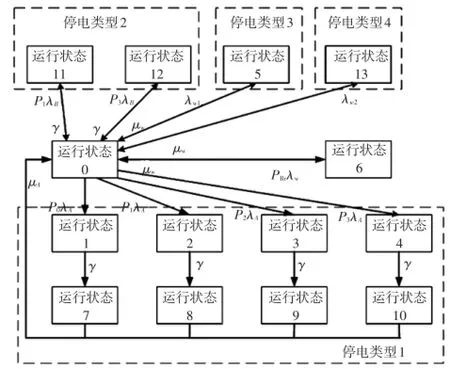
图2 输电线路A的完整Markov状态模型Fig.2 Complete Markov model for transmission line A

模型中所需各参数的定义如下：P0为线路故障时两端保护系统均能正确动作的概率，P1和P2分别为左右两端保护系统发生拒动的概率，P3为两端保护系统同时出现拒动的概率，PP、PBr分别为保护装置和断路器的拒动概率，λA、μA分别为线路A的失效率和修复率，λB为相邻B线路的失效率，γ为故障元件的保护拒动造成停电范围扩大后，恢复邻近元件和隔离故障元件的效率［14］，λw1、λw2分别为系统无故障保护误动及保护非选择性误动时的失效率，λw为总的保护误动率，数值上等于λw1与λw2之和，μw为保护发生误动失效时对应的修复率。

模型中运行状态0表示线路及保护系统均正常。当线路A发生故障后，系统状态转移分为以下2类情况：①若两端保护及断路器均正常动作，线路将由状态0转移到状态1，待人工检查及确认后线路进入状态7，最后经过修复过程，线路回到状态0；②若两端保护或断路器发生拒动时，相邻设备的保护将作为远后备保护动作，此时将导致相邻一次设备的无故障停运。例如线路左端RA1或A1拒动时，线路将从状态0转移至状态2，此时线路A、B均被切除，经过人工检查及倒闸恢复多切设备（线路B）供电后，线路由状态2进入状态8，故障线路修复完成后，线路回到状态0。当线路正常而保护发生第一类误动失效时，线路会由状态0转移到状态5，经过保护修复过程后，线路恢复供电，回到状态0。

当线路A及其保护正常，但相邻下一级线路B发生故障后且其左端保护或断路器出现拒动线路A的保护将作为后备保护动作，造成线路A停运。此时，线路A由状态0进入状态11；同理，当线路B故障且其两端保护或断路器同时拒动时线路A由状态0转移至状态12。经过人工检查及倒闸操作，线路A可恢复供电，回到状态0。若线路B发生故障后且其两端保护与断路器均正确动作，但此时可能由于系统运行方式变化导致线路A的保护发生非选择性误动，线路A将由状态0转移至状态13，保护修复完好后回到状态0。

图2中状态1～4、7～10以及状态5分别属于线路的停电类型1和停电类型3，且均是由线路A及其保护故障引起，属于自发故障停运；状态11、12以及状态13则分别对应于线路的停电类型2和类型4，且其均是由相邻线路的故障所引起，属于诱发停运。

另外，考虑断路器失效后，会出现一种特殊的状态，即保护装置发生误动（包括2种误动情况）且断路器拒动的情况，如图2中的6状态所示，此状态下线路仍然保持正常运行，故没有包括4种停电类型之中。但此时保护系统存在故障，且属于隐性故障的一种，拟在继电保护可靠性及风险分析中加以考虑，限于篇幅，将另文讨论。

断路器的拒动和保护装置的拒动对被保护设备和整个电力系统的影响相同，故障线路的正确切除需要保护和断路器配合完成。因此，当计及断路器拒动失效的影响后，P0～P3的表达式为

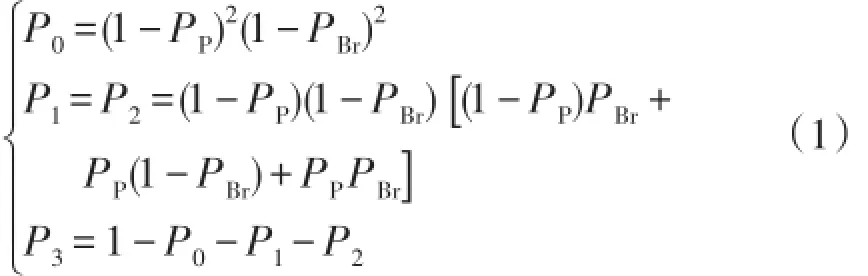
不考虑断路器失效时，P0～P3则分别表示线路两端保护装置均正确动作、左右两端保护装置分别拒动和两端保护装置同时拒动的概率，计算方法将有所不同，即

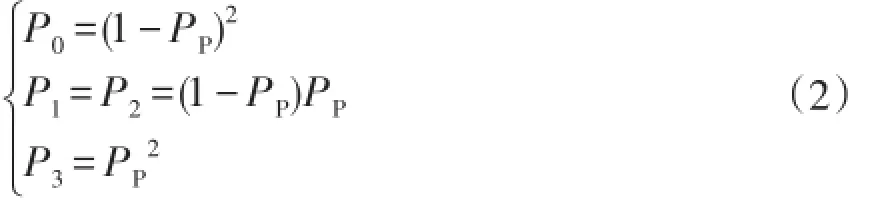
如上分析，考虑断路器拒动和保护非选择性误动的失效影响后，将使线路的模型参数更加准确，模型中的状态进一步完善，从而使线路模型更加符合实际运行状况。

类似方法，可以建立线路B的可靠性分析模型。当系统中的所有线路的可靠性模型均建立完成之后，就完成了系统的可靠性建模。可以看出，当计及保护和断路器的失效时，一方面将使线路的运行状态增多，另一方面，会使相邻线路之间的故障不再独立，即由于保护间的协调配合会导致相邻设备间存在耦合失效。如何准确模拟线路各状态间的转移及相邻设备间的耦合失效关系是获取精确可靠性评估结果的关键。

3 计及保护失效的输电系统可靠性计算

建立了各设备的状态转移结构图之后，对于简单系统，可以应用状态枚举法或Markov状态空间法对系统进行可靠性分析；对于实际大规模系统，一方面考虑保护影响后线路状态较多（14状态），另外系统中的元件数也多，相应系统状态总数随着元件的增多呈指数性增长，因此这两种方法较难适用于实际系统的可靠性评估计算。本文采用序贯蒙特卡洛仿真法对于按第2节所建立的状态转移图进行仿真模拟，进而获得系统的可靠性指标。

3.1 系统可靠性指标

本文常用的系统可靠性指标［15］如下。

（1）系统失负荷概率LOLP（loss of load probability）为

式中：S为系统有切负荷状态的集合；ti为系统状态i的持续时间；T为总仿真时间，a。

（2）系统失负荷频率LOLF（loss of load frequency）（次/a）为

（3）平均切负荷持续时间ADLL（average duration of load loss）（h/次）为

近年来，国企频繁进行改革改制、重组、收购等操作，对应企业的管理模式、经营体系、产权结构等也随之发生改变。国企充分落实深化改革要求的较少，但是进行结构调整、规模扩张的趋势较为突出。企业审计团队的规模逐渐朝着稳定化方向发展，审计对象缩小，但是审计内容大幅扩张，增加了相关作业人员的工作量；同时深化改革下，逐步突破了地域界限、行业界限，导致审计监督工作的难度大幅增加；此外，改革后，一些企业的收入、负债等存在较大偏差，降低了同期数据的可参考价值，受会计评估等政策的改变，深化改革下审计难度大幅增长。

（4）电力不足期望值EENS（expected energy not supply）（GW·h/a）为

式中：Ci为系统状态i的切负荷量；Ni为有切负荷的状态数。

3.2 计及保护失效的输电网序贯蒙特卡洛仿真

序贯蒙特卡洛方法通过比较各设备当前状态持续时间来确定当前系统状态的持续时间，并按照时间推进对系统运行状态转移进行模拟，因此该方法在计算与系统的频率和时间相关的可靠性指标方面具有明显优势。假设线路以及变压器支路（简称为线路），在图2中的各状态的持续时间为满足指数分布的随机变量，则其抽样公式为

式中：r为区间（ ）0,1上均匀分布的随机数；ti为线路状态持续时间，具体包括设备正常工作时间、修复时间以及倒闸操作时间；ρi为与ti对应的状态转移率，包括失效率、修复率和倒闸率。

相关变量及假设说明：tk表示从0时刻到第k个系统状态末的总系统仿真时间；n为系统中的线路总数；Ti,k-1和Ti,k分别为第k-1个和第k个系统状态下线路i的状态持续时间；Dk-1和Dk分别为第k-1个和第k个系统状态的持续时间。则计及保护失效及断路器失效后输电系统可靠性评估算法的计算步骤如下。

步骤1 设定初始条件。仿真时刻初值t0=0，系统状态计数器k=0，系统中所有线路的初始状态均为正常工作状态，即状态0。

步骤2 确定系统初始状态持续运行时间。由于线路初始时均处于状态0，线路本身或其保护系统的不同失效将导致线路转移至不同的状态（状态1～6）。因此，首先要抽样生成线路i（i=1,2, …,n，n为系统中的线路总数）处于初始正常工作状态的持续时间T0，i及下一运行状态。具体过程为：产生6个随机数ri,1～ri,6，并根据式（7）及6个状态转移率计算得到对应的状态持续时间ti,1～ti,6，选取其中最小的状态持续时间作为该线路当前状态的持续时间Ti,0，不妨设该最小状态持续时间为ti,z（z=1,2,…,6），则Ti,0=ti,z，同时可确定该线路的下一运行状态为状态z。若所有线路的状态持续时间及下一状态确定之后，系统在初始状态的持续时间；仿真时钟推进到t1=D0，k=k+1。

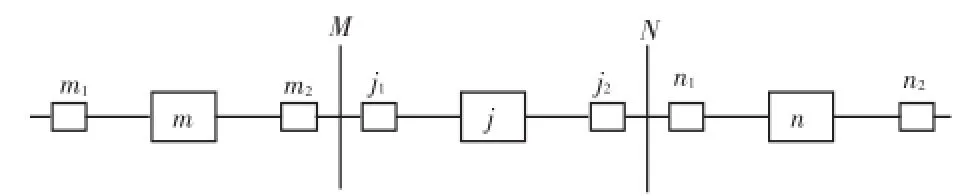
图3 线路j及其相邻线路Fig.3 Line j and its adjacent lines

（1）若线路j处于状态0且其两端相邻线路（m 或n）由状态0转移至状态1（即意味着相邻线路发生了停运诱发事件）时，产生一个新的随机数rj并与保护非选择性误动概率Pmal进行比较。若rj＜Pmal，则将线路j转移至状态13；

（2）若线路j处于状态0且其右侧相邻线路n由状态0转移至状态2，同样意味着发生了停运诱发事件，此时将线路j由状态0转移至状态11；类似方法，若线路j的左侧相邻线路m由状态0转移至状态3或两端相邻线路由状态0转移至状态4时，则将线路j的状态转移至状态11或12；

（3）若线路j处于状态11且其右侧相邻线路n由状态2转移至状态8，则将线路j的状态置为0，此过程对应于人工检查及倒闸操作结束后，将非故障停运线路恢复供电；若线路j的左侧相邻线路m由状态3转移至状态9或两端相邻线路由状态4转移至状态10时，处理方法为：将线路j由状态11 或12转移至状态0；

步骤4 计算系统当前状态下所有线路i （i=1,2,…,n）的状态持续时间Ti,k，并确定该线路的下一运行状态。相比于上一系统状态，在当前系统状态下只有部分线路发生了状态转移，大多数线路的状态未发生变化。对于状态发生转移的线路，需确定其状态持续时间及下一状态；对于未发生状态转移的线路，只需确定其状态剩余持续时间，其下一运行状态已在此前系统状态确定。具体过程如下。

（1）确定所有未发生状态变化的线路在本系统状态下的各自剩余持续时间，即：若Ti,k-1＞Dk-1，i=1,2,…,n，则线路i在当前系统状态的持续时间为其所在状态的剩余时间，即为Ti,k=Ti,k-1-Dk-1；

（2）确定所有发生状态转移线路的状态持续时间及其下一运行状态，即：若Ti,k-1=Dk-1,i=1, 2,…,n，则线路i的当前状态持续时间Ti,k分为以下3种情况进行计算：

①当线路i处于状态0时，则产生6个随机数ri,1～ri,6。根据式（7）及6个状态转移率计算得到对应的状态持续时间ti,1～ti,6，选取其中最小的状态持续时间作为该线路当前状态的持续时间Ti,k，不妨设该最小状态持续时间为ti,z（z=1,2,…,6），则Ti,k=ti,z，同时可确定该线路的下一运行状态为状态z；

②当线路i处于状态11或12两种诱发故障状态时，其转移至下一状态（状态0）是一个被动过程；因此，线路i的状态持续时间由相邻故障线路的倒闸操作时间决定：；其下一状态为状态0；

③当线路i处于状态1～10或状态13时，根据图2中线路各状态之间的转移关系，即可确定该线路下一运行状态，同时根据对应的状态转移率及式（7）计算得到其当前状态的持续时间Ti,k。

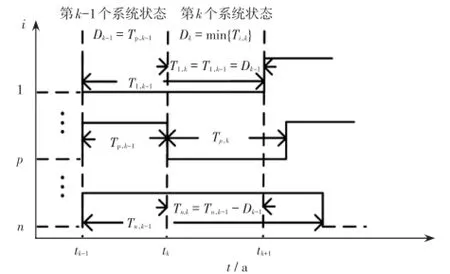
图4 第k个系统状态下线路状态持续时间的计算Fig.4 Calculation of state durations of lines in system state k

上述步骤4中的状态确定过程如图4所示。图中曲线1、p、n分别代表3条线路各自的运行状态曲线，其他线路运行状态曲线分析方法类似。在图4中，线路p在第k-1个系统状态末发生状态转移，而线路1、n未改变状态。因此在第k个系统状态下根据式（7）计算线路p的状态持续时间，而线路1、n在第k个系统状态下的状态持续时间为其各自的状态剩余持续时间。

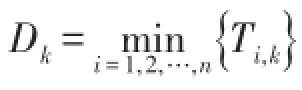
步骤6 计算当前系统状态的负荷损失：从tk至tk+1系统状态维持不变，根据当前系统状态下各个线路的状态，进行当前系统状态下的负荷损失计算。负荷损失的计算流程如下：

（1）若当前系统状态下没有线路停运，则负荷损失量为0，转至步骤7；

（2）若当前系统状态下有部分线路停运，则进行直流潮流计算以验证是否有线路传输功率越限；若出现线路传输功率越限，则进行基于直流OPF的最小切负荷计算，实现发电机出力重调基础上的最小切机及切负荷以消除线路越限，该最小切负荷量即为当前系统状态下的负荷损失量；否则该状态下没有负荷损失，转至步骤7。

步骤7 若仿真时间达到设定的结束时刻，统计整个仿真过程的各个参数，并按式（3）～式（6）计算系统可靠性指标，程序结束；否则，k=k+1，并转至步骤3，继续进行下一系统状态的仿真。

算法流程如图5所示。

4 算例分析

本文采用IEEE-118节点标准测试系统验证本文算法的有效性和正确性。节点及支路参数参见文献［16］，保护系统原理性误动概率Pmal及其他可靠性基础参数，以及线路的失效率λL、修复率μL、传输功率上限Pmax如表1所示。本节主要侧重对本文所建模型和所提方法的验证，因此对模型和元件参数做一定假设和简化处理：表1为各参数根据实际运行经验及相关文献中的典型参数［9］取值，且本文假定所有保护及各线路的可靠性参数均相同。

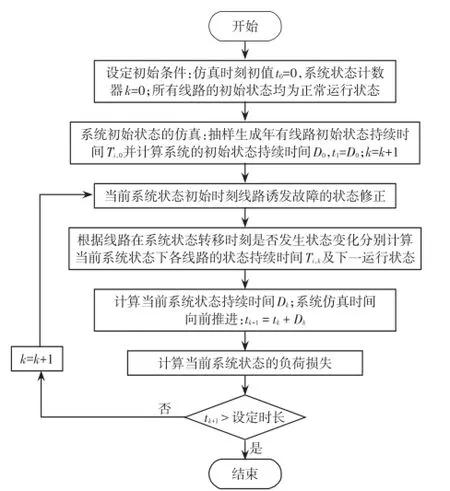
图5 计及保护失效的输电系统可靠性评估流程Fig.5 Flow chart of reliability evaluation for transmission system including protection system failures

表1 保护及线路有关的可靠性参数Tab.1 Reliability parameters associated with lines and protection systems

图6为采用本文模型计算LOLP及LOLF随仿真时间增长的动态变化曲线。由图可看出，两指标在380 a左右开始趋于稳定。因此本文设定仿真时长为400 a。

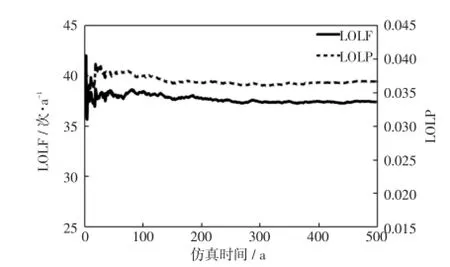
图6 LOLP及LOLF随仿真时长的变化曲线Fig.6 Variance curves of LOLP and LOLF in the simulating process

分别采用本文方法、文献［9］方法以及不考虑保护失效时的线路两状态模型及方法［17］对算例系统进行仿真计算，仿真时间长度为400 a，各个方法的可靠性指标计算结果如表2所示。

对比前两组结果可以看出，基于不同方法的系统可靠性指标明显不同：本文方法结果中LOLP、LOLF和EENS3个指标较大，而ADLL指标则较小；这是由于考虑断路器的拒动和保护非选择性误动的影响后，一方面，线路的运行状态及停电状态总数相比于文献［9］中的方法均进一步增多，另一方面，断路器的拒动以及保护的非选择性误动失效会分别增加相邻线路和被保护线路本身的停运概率，使得系统的可靠性降低。因此，LOLP、LOLF和EENS3个指标会有所增大。另外，新增的停电状态持续时间较短，因而造成系统的平均切负荷持续时间ADLL出现下降。对比本文方法和两状态方法结果可以发现，相比于未考虑保护失效时评估结果，计及保护及断路器失效影响的各系统可靠性指标变化趋势同上述一致，但变化更加明显。

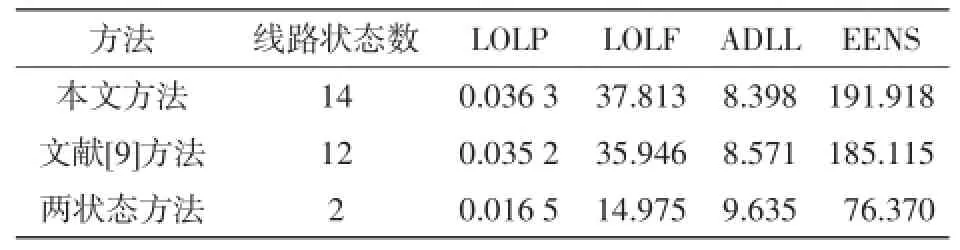
表2 基于3种不同方法计算得到的算例系统可靠性指标Tab.2 System reliability indexes respectively by three different methods

为了进一步验证本文方法的准确性，进一步计算负荷增长10%后的系统可靠性指标，计算结果如表3所示。

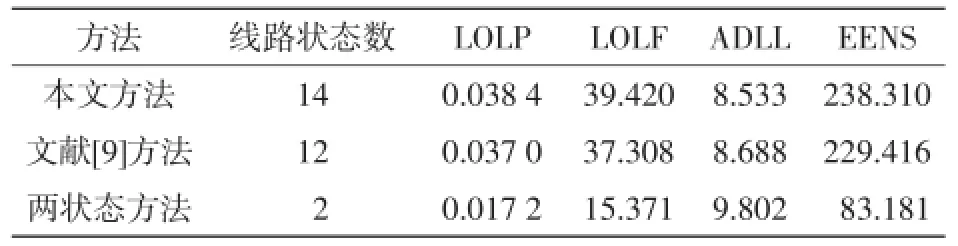
表3 1.1倍基准负荷水平时系统可靠性指标Tab.3 System reliability indexes with 1.1-fold load level by three different methods

对比表2、表3可知：系统负荷水平增长后，系统可靠性出现降低，但采用3种方法计算时系统可靠性的下降幅度会有所差异：以LOLP指标（指标越小表明系统可靠性越高）为例，其基于3种方法的计算结果分别增大5.7%、5.1%和4.2%，也就是说基于本文所提出的包括断路器拒动及保护非选择性误动的完整系统可靠性分析计算所得到的可靠性指标增大最多；由此可以得出，负荷水平提升时，断路器拒动及保护非选择性误动对于系统可靠性的影响加大；若不计及其影响，所得到的可靠性指标偏保守。

上述结果和分析表明：本文所建立的线路状态模型更为完整，且更加符合实际的运行状况，因而基于本文方法的到的评估结果（不同负荷水平时）更能反映系统的真实可靠性水平；同时，也验证了在电力系统可靠性评估时计及保护及断路器失效影响的必要性。

5 结语

本文提出了基于线路完整模型及序贯蒙特卡洛仿真的输电系统可靠性分析新方法。结合保护拒误动、断路器失效及保护系统之间的配合对线路停运的影响，本文建立了计及保护、断路器失效影响的输电线路完整Markov状态分析模型；并根据此模型，采用序贯蒙特卡洛方法，对包括一、二次设备的电力系统状态进行抽样仿真而实现了完整电力系统的可靠性分析。由于本文所建立的线路状态模型完整，且更加符合实际的运行状况，从而基于本文模型所进行的系统可靠性分析结果的准确性及可信性更高。

［1］Johannesson T，Roos F，Lindahl S.Reliability of protection systems-operational experiences 1976—2002［C］//8th International Conference on Developments in Power System Protection.Amsterdam，Netherlands，2004：303-306.

［2］邓丰强，吕飞鹏（Deng Fengqiang，Lü Feipeng）.考虑保护重要度的继电保护定值在线校核（On-line verification of relay protection setting considering protection importance）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（4）：85-90.

［3］Phadke A G，Thorp J S.Expose hidden failures to prevent cascading outages［J］.IEEE Computer Applications in Power，1996，9（3）：20-23.

［4］孙元章，周家启.大型互联电网在线运行可靠性的基础理论［M］.北京：清华大学出版社，2010.

［5］Vadlamudi V V，Gjerde O，Kjolle G.Incorporation of protection system failure modes in composite power system reliability studies［C］//7th Annual CIGRE Canada Conference on Power Systems.Montreal，Canada，2012：1-12.

［6］Vadlamudi V V，Gjerde O，Kjlle G.Dependability and security-based failure considerations in protection system reliability studies［C］//4th IEEE/PES Innovative Smart Grid Technologies Europe，Lyngby，Denmark，2013：1-5.

［7］付聪，安灵旭，方华亮，等（Fu Cong，An Lingxu，Fang Huangliang，et al）.继电保护系统对一次设备可靠性的影响研究（Study on the influence of protection system on reliability of primary equipment）［J］.电力系统保护与

控制（Power System Protection and Control），2013，41 （11）：38-44.

［8］Pottonen L.A Method for the Probabilistic Security Analysis of Transmission Grids［D］.Helsinki：Helsinki University of Technology，2005.

［9］Jiang Kai，Singh Chanan.New models and concepts for power system reliability evaluation including protection system failures［J］.IEEE Trans on Power Systems，2011，26（4）：1845-1855.

［10］VDN.Ermittlung von Eingangsdaten für Zuverlässigkeitsberechnungen aus der VDN Störungsstatistik［EB/OL］.http：//www.vde.com/de/fnn/arbeitsgebiete/vesorgungs quat-aet/seiten/versorgungszuverlaessigkeit-unterlagen.aspx，2012.

［11］王家林，夏立，吴正国，等（Wang Jialin，Xia Li，Wu Zhengguo，et al）.采用量子遗传算法的船舶电网故障诊断方法（Fault diagnosis method of shipboard power system using quantum genetic algorithm）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（3）：35-39.

［12］Singh C，Patton A D.Models and concepts for power system reliability evaluation including protection system failures［J］.International Journal of Electrical Power& Energy Systems，1980，2（4）：161-168.

［13］王献林，吕飞鹏（Wang Xianlin，Lü Feipeng）.继电保护可靠性及其状态检修方法（Relay protection reliability and its state overhaul method）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2014，26（9）：65-70.

［14］张雪松，王超，程晓东（Zhang Xuesong，Wang Chao，Cheng Xiaodong）.基于马尔可夫状态空间法的超高压电网继电保护系统可靠性分析模型（Reliability analysis model for protective relaying system of UHV power network based on Markov state-space method）［J］.电网技术（Power System Technology），2008，32（13）：94-99.

［15］郭永基.电力系统可靠性分析［M］.北京：清华大学出版社，2003.

［16］吴际舜，候志俭.电力系统潮流计算的计算机方法［M］.上海：上海交通大学出版社，2000.

［17］李文沅，周家启.电力系统风险评估：模型，方法和应用［M］.北京：科学出版社，2006.

Transmission Network Reliability Evaluation Considering Protection Failures

ZHANG Zhanlong1，YAO Li1，LEI Linxu2，LIN Jikeng3，WEI Wenhui4，HAN Jiabing4
（1.School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2.State Grid Smart Grid Research Institute，Beijing 102200，China；3.College of Electronic and Information Engineering，Tongji University，Shanghai 201804，China；4.Beijing Kedong Electric Power Control System Limited Company，Beijing 100085，China）

How to improve the accuracy of the reliability analysis of transmission system is a hot topic that has aroused extensive concerns in power system reliability analysis.Based on the analysis of line outage under the two types of protection failures，the failure of circuit breaker and cooperation of protection system in between，a new reliability analysis approach on transmission system is presented based on the complete Markov model of line states and sequential Monte-Carlo simulation.A complete Markov model is established first for transmission lines considering failures of protection and circuit breaker.Then，simulation of system states resulted from primary equipment and secondary equipment are carried out by sequential Monte Carlo method and reliability indexes are calculated，thus realizing the reliability analysis of a whole power system.Since the proposed line states model is complete and consistent with actual operating conditions，the results of system reliability analysis based on this model are more accuracy and credibility.Examples prove the validity of the raised method.

reliability assessment；protection failures；circuit breaker non-operations；sequential Monte-Carlo simulation；Markov model

TM732

A

1003-8930（2016）01-0079-07

10.3969/j.issn.1003-8930.2016.01.014

2014-10-11；

2015-02-04

国家电网公司总部科技项目（新一代智能变电站保护、控制及通信技术实用化研究）

张占龙（1988—），男，硕士研究生，研究方向为继电保护及电力系统可靠性。Email：langshena@126.com

么 莉（1963—），女，硕士，副教授，研究方向为电机磁场分析、电机电器设计。Email：yaoli@tju.com.cn

雷林绪（1965—），男，硕士，高级工程师，研究方向为电力电子技术在电力系统的应用。Email：leilinxu@sgri.sgcc.com.cn