基于小波包和样本熵的齿轮故障特征提取

赵鹏飞杨喜旺沈松黄晋英崔小龙

基于小波包和样本熵的齿轮故障特征提取

赵鹏飞1，2杨喜旺1沈松2黄晋英1崔小龙1，2

1、山西中北大学计算机与控制工程学院2、北京东方振动和噪声技术研究所

针对齿轮箱振动信号的复杂性和随机性，本文采用在时、频域内能更好地反映信号本质特征的小波包分解方法进行分析处理，然后用样本熵作为特征向量，首先把采样得到的时域数据进行三层小波包变换，然后计算分解获得的所有频段的样本熵，用来当作特征值。通过MATLAB实现算法，并用齿轮箱实验台模拟正常、齿顶磨损、断齿三种工况进行实验和分析验证了该方法的有效性。

齿轮；小波包；样本熵；特征提取

引言

齿轮箱作为一种常用的零件，在煤矿机械、工厂机床、交通运输等领域有相当高的使用率，已经成为机械器材中不可或缺的连接和传动部件。然而，因为齿轮箱的组成复杂，运行强度高，极易产生故障，其中齿轮发生故障的概率达到60%，所以对其振动信号的分析与预测故障的发生有着重要意义。

实际工程中，振动信号含有齿轮箱组成部件的各种振动，并且混杂着各种噪声信号，使信号表现出非平稳性。使用传统手段解析此类数据，只能在时间域或频率域中，无法得到全面的结果。而小波变换则是一种在时频两域描述信号的算法，能更好地反映信号的本质特征，并且有多分辨率的特点，能像显微镜一样逐渐精细地观测信号。小波包的优势在于它的分辨率更高，能够把信号分解得更详尽。在装置产生异常的时候，故障信号的繁杂性和不规律性能够体现故障的出现和发展。关联维数、近似熵、多尺度熵、样本熵等都可以体现信号的复杂程度。其中样本熵作为近似熵的改进，已被广泛运用于生物医学，它的优点在于较少地依赖时间序列长度，比近似熵能更好地反映系统的本质。文章利用小波包变换和样本熵，从齿轮故障信号中提取特征向量，并以此来区分齿轮状态，实验证明该方法很有效。

1小波包和样本熵结合的特征向量构造方法

1.1小波包理论

小波包变换是在小波的基础上提出的能加倍细密解析信号的算法。对比小波变换，小波包克服了它在较高的频率分段分辨率和对低频率分段的时间分辨率的不足，有更强的分辨力。

设Vj；j∈｛｝Z（Z是整数集）构成L2（R）正交多分辨率分析，它的尺度函数与之对应的小波函数分别是φ（t）、ψ（t），并满足差分方程

上式当中，hk与gk是一对正交滤波器，符合如下条件：在尺度不发生改变的状态下，递归函数记作：

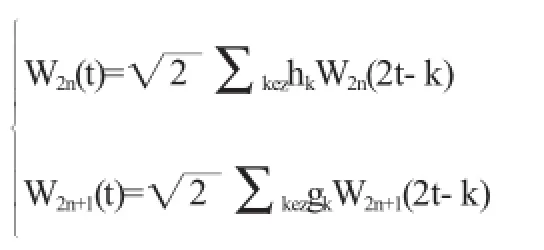
我们把上面式子所决定的Wn（t）（n=0，1，2，…，N）叫作以正交尺度函数W0=φ所决定的小波包。

1.2样本熵理论

样本熵先进的地方在于它弥补了以往特征参量需依赖庞大的数据量的缺点。样本熵不依赖数据长度，而且它在数据比较少的情况下能得到比近似熵更稳定、精度更好的结果，所以它有更强的鲁棒性。样本熵也被大量运用于生物信号中，有了大量的实验验证。而设备故障信号与生物信号都属于非平稳随机过程，故而使用样本熵来度量振动信号。

通常，x（n｛｝）=（1），x（2），…，x（N）是N个数据按发生时间先后构成的一组数列，它的样本熵计算方法如下：

（1）构造由m个向量构造的向量组，按编号顺序排序：Xm（1），…，Xm（N-m+1），其中Xm（i）=｛x（i），x（i+1），…，x（i+m-1）｝，1≤i≤N-m+ 1。向量序列表示的是数列从第i到第i+m的值。

（2）将向量Xm（i）与Xm（j）中间的距离d［Xm（i），Xm（j）］定义为两向量相应时间序列中最大差值的绝对值。

（6）定义Am（r）为：

这样，样本熵定义为

表1　各种故障下数据样本熵对比

1.3小波包和样本熵构成齿轮信号特征向量

（1）将采集到的齿轮箱正常和故障振动数据用小波包分解，能获得被分解到不同频段的频带系数；

（2）把获得的小波包系数采用算法获得重构信号，分别求得重构信号的样本熵值；

（3）将每个频率段算出的值作为元素，组成振动数据的特征向量。

2实验与结果

本实验采用INV1618故障模拟实验台模拟齿轮故障，齿轮状态包括正常、断齿、齿顶磨损三种类型，齿轮的损伤状况为单一损伤。前端的测量装置使用INV9822加速度传感器，安装在齿轮箱侧面水平方向进行测试，实验现场（图1）。

图1　实验台及采集器布置示意图

三种齿轮状态的原始振动信号时域波形，从时域波形中不能轻易辨别齿轮的状态。

于是将原始的振动信号用小波包分解，分解至第三层，小波包的确定参照文献［2］的结论选择DB12小波，通过2^3尺度分解后，得到频率范围从0～19.69kHz的8个频带。对处理后获得的8个频率区间的系数使用重构算法，最后获得每个频率区间的重构信号。其中以断齿故障信号为例，经过小波包分析后得到信号波形（图2）。

图2　断齿故障信号重构信号

根据文献［3］的研究结果，m=1或2，r=0.1～0.25Std（Std为原始数据x（i）的标准差，i=1，2，…，N）时，可以获得的结果更符合统计特性，在计算时向量维数取2，而相似容限为0.25Std。构造特征向量，把算出的每个频率范围的结果当作其元素，获得八维的向量。正常、齿顶磨损、断齿情况下的齿轮箱样本熵数值见表1。不难看出，在齿轮箱工况有差别的状况下，计算得到的样本熵都有区别，如此表示样本熵能够作为判断齿轮箱故障的特征。

3结论

文章选择了一个采用小波包分析结合样本熵计算的方式来获得齿轮故障特征向量。对齿轮完好、断齿、齿顶磨损三类故障工况进行分组实验。通过对实际齿轮信号进行分析计算，从结果中不难了解，不同工况下振动数据样本熵的值会有明显差异，表明可以将样本熵当作齿轮故障信号的特征值，证明了该方法确实可行，为后续的故障判断打好了基础。

［1］丁康，朱小勇.齿轮及齿轮箱故障诊断实用技术［M］.北京：机械工业出版社，2006.

［2］Nikolaou N G，Antoniadis I A.Rolling elementbearing fault diagnosis using wavelet packets［J］.NDT&E International，2002，35（3）：197-205.

［3］Pincus S M.Assessing serial irregularity and itsimplications for health［J］.Annals of the New YorkAcademy of Sciences，2002，954：245-67.