航路资源分配下的航班时刻优化
陈亚青 宋 斐 罗 亮
航路资源分配下的航班时刻优化
陈亚青 宋 斐 罗 亮
本文分析了航路资源合理分配的必要性,以航路上所有航班的总延误成本最小为目标函数,以航班时刻变动范围、时刻数量和航路容量限制为约束条件,建立了航路耦合容量模型和航班延误成本模型。再以京-沪航路航班数据为基础进行算例分析,运用匈牙利算法求解模型。计算结果表明:新增了10个航班时刻;缩短了11个航班的延误时间;优化后航班最小总延误成本明显降低。通过改航到临时航线,使其利用率提高了43.5%;各飞行航段的实时流量与容量限制更加匹配,降低了空中交通延误时间。
随着我国民航业的快速发展,航班延误问题日益凸显,严重影响了旅客出行需求和民航的发展。对于航空公司而言,航班时刻是非常重要的资源,是占有市场的直接体现,但大量航班延误导致航空公司非正常运行成本的急剧攀升。如何利用科学的方法优化航班时刻分配,缓解延误,一直是全球民航界关注的重点问题之一。
国外对于航班时刻优化主要集中在地面等待策略的研究。1987年,Romanin Jacur等人试图通过建立数学模型解决地面等待时间分配的问题。2003年,Michael等人深入研究了更易于与协同决策系统集成的地面等待策略双层网络结构整数规划模型。2011年,Dimitris Bertsimas等人提出了一个考虑公平性和航空公司协作的航班时刻优化分配网络模型。
国内对于航班时刻优化的研究主要通过基于多机场地面等待策略建立的模型和算法进行的。1998年,胡明华教授对多机场地面等待策略问题进行了建模求解,并研发出一套航班时刻规划专家系统。2010年,张洪海等人提出了体现公平性、工效性和有效性的协同地面等待时刻分配优化算法,给出了一种多目标优化模型。2013年,朱承元等人采用空域机场仿真模型(SIMMOD)对珠三角地区多机场系统的航班时刻优化分配进行了仿真研究。
上述研究主要是基于地面等待策略实现对航班时刻的优化,本文通过考虑管制单元之间的航路耦合容量限制,将空域拥堵转化为航路拥堵问题,并基于临时航线建立航班时刻优化模型,为延误航班分配时刻提供决策依据。
模型建立
本文中的“航路”是包括起飞机场、航路、落地机场的一个整体。通过研究航路资源分配的约束条件,建立相应的模型。
在N 个空域管制单元的耦合约束下,航路r在t时间片的运行容量为:
航路耦合容量模型
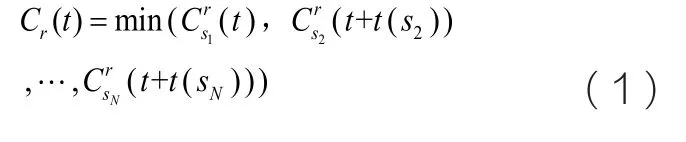
其中,
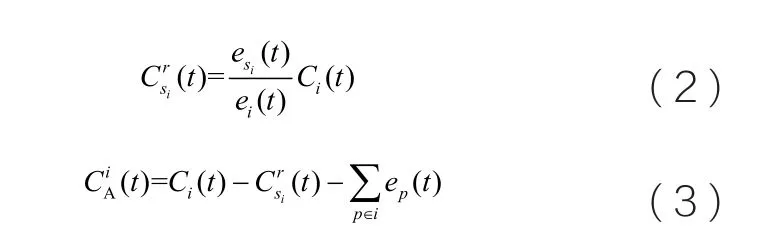
航班延误成本模型
航班的成本函数定义如(4)式:
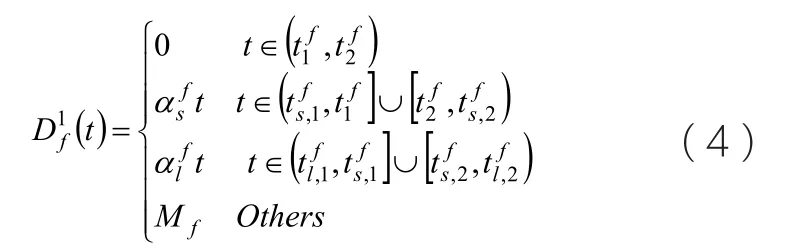
航班的改航成本函数如(5)式:
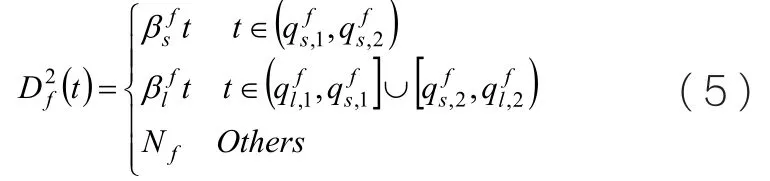
基于航路资源分配的航班时刻优化模型
本文假设所有的航班都是可以调整航班时刻的。模型中所涉及的参数含义如下:
T:T={1,2,…,t}为每15min一个时间片;
F={1,…,f}是一个城市对之间的航班序列;
K={1,…,k}为机场集合,k 为起飞机场,k′为落地机场;
M :航路资源集合,其中m∈M 表示计划航路,n∈M表示临时航线;
Cm(t):在时间片t内计划航路m 的耦合容量;
Cn(t):在时间片t内临时航线n 的耦合容量;
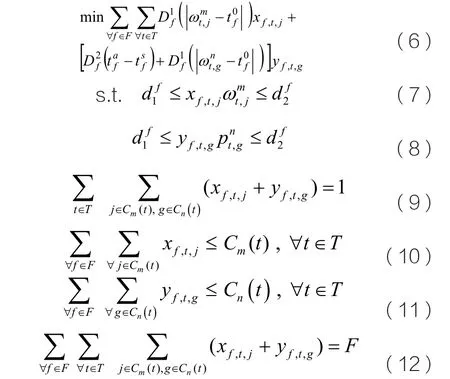
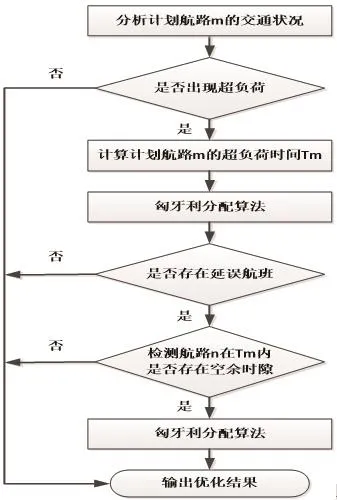
图1 求解流程
算法设计
航班时刻优化问题属于战略流量管理范畴,因此在设计算法时可以任意调整时刻。另外,航班时刻的分配问题是0-1整数规划问题,亦为指派问题。当时刻数大于或小于航班数时,是非标准的指派问题,通过添加虚拟航班或时刻化为标准的指派问题,并使用匈牙利算法进行求解。优先分配计划航路上的时刻,同时设置较大的改航成本系数,使航班分配到临时航线作为次优策略。求解流程如图1所示。
算例验证
算例描述
本文采用《2014夏秋国内公司航班计划》,星期一7:00-22:00时间段中从北京首都机场飞往上海虹桥和浦东机场的50架航班进行仿真和分析,将北京首都机场作为航班的决策点。计划航路(R1)和临时航线(R2)所经过的空域管制单元的小时容量及在各空域管制单元飞行的时间如表1所示。其中,ZBAAR04,ZSSSAR06分别表示北京区域管制04号扇区和上海区域管制06号扇区,其余同理。
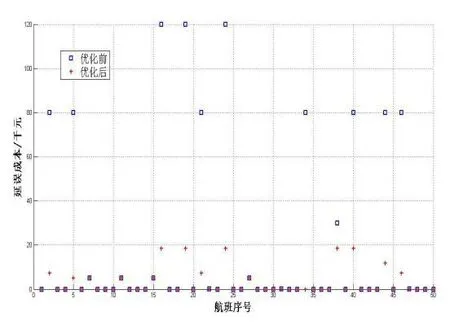
图2 航班延误成本对比
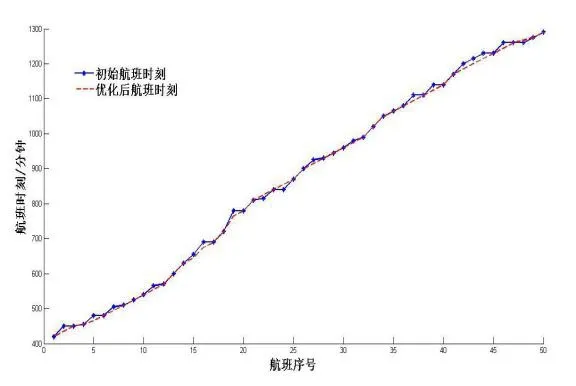
图3 航班时刻优化对比
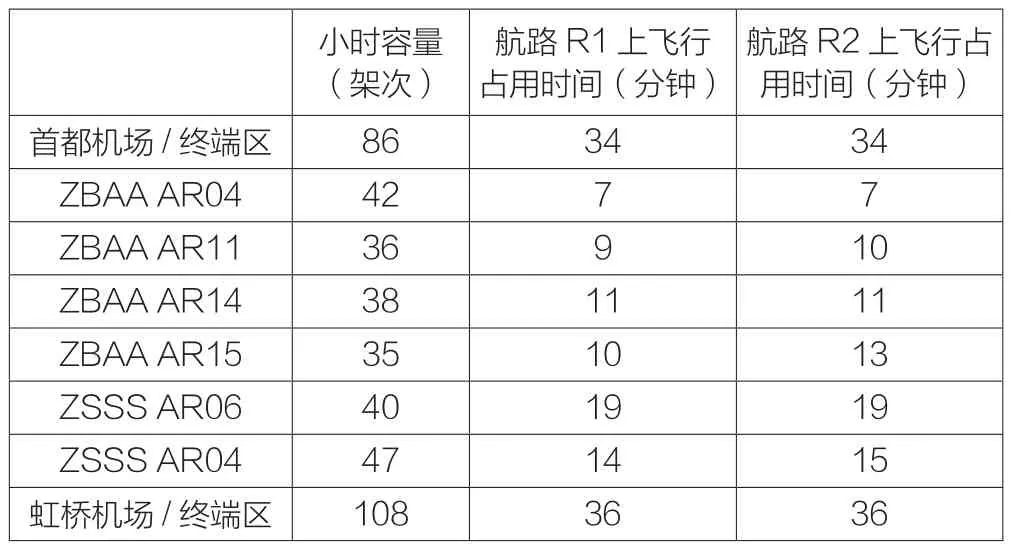
表1 空域管制单元容量及航班飞行时间
算例分析
通过航班时刻仿真评价系统,结合航段在所属扇区的流量需求比例以及扇区容量约束下的航段容量,计算航路R1、R2在各时间片内的航路耦合容量和航段容量,进而得出航路R1有40个时刻,航路R2有23个时刻。计划航路上的40个时刻明显不能满足50架航班的需求,18架航班产生延误,航班最小总延误成本为970340元。将第一次分配后产生延误的航班时刻与临时航线上的航班时刻合并,进行二次优化分配,优化后发生延误的航班仍有17架,但其中10架被分配到临时航线上,最终得到航班最小总延误成本为151340元。每架航班的延误成本变化如图2所示。
图3以分钟表示时间给出了优化前后给50架航班分配的时刻变化,优化后新增了10个航班时刻,较初始的航班时刻分配更加平滑,不会出现同一时刻分配给多架飞机的情况,航班时刻分配更加合理。临时航线的利用率提高了43.5%,航路资源分配更加高效。
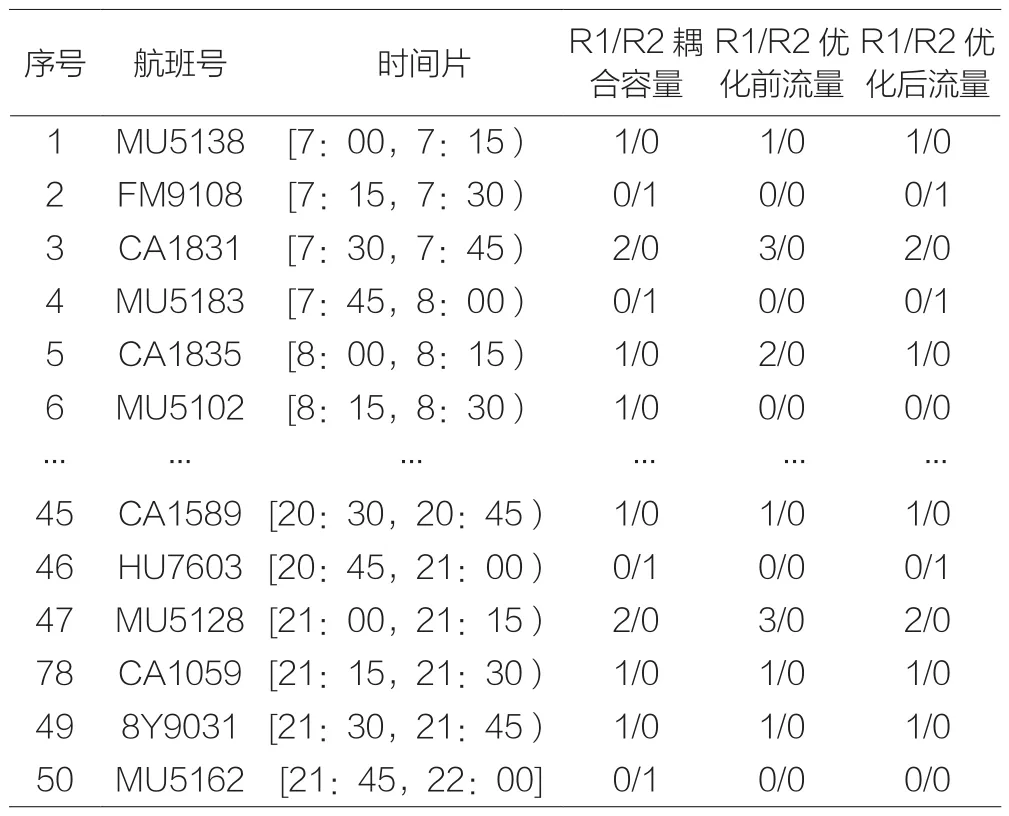
表2 航路的容量和流量对比
表2表示了优化前后航路的容量和流量对比。如CA1831航班所在时间片[7:30,7:45)内,优化前航路R1的流量大于耦合容量,必然会产生延误;优化后航路R1的耦合容量和流量更加匹配、降低了空中交通延误时间。这表明本文所建立的航班时刻优化模型和设计的求解算法是有效的。
结语
本文对基于航路资源分配的航班时刻优化问题进行了研究,建立了相应的航路耦合容量模型和航班延误成本模型,并通过具体案例进行分析。研究结果表明:以起飞机场为决策点全局考虑整个飞行过程中的容量限制,优化后部分航班改航到临时航线上,航程增加,但总的延误成本大大降低,同时减少了空中交通延误时间,提高了临时航线利用率。由于航班延误成本参数借鉴了欧控的相关文件,为更真实的反映我国航班运行情况,进一步需要加强对航班延误成本参数的研究。

陈亚青1宋 斐2罗 亮3
1.中国民用航空飞行学院民航飞行技术与飞行安全科研基地;
2.中国民用航空飞行学院空中交通管理学院;3.中国民用航空青岛空中交通管理站
陈亚青(1970 -)男,山西原平人,硕士,教授。研究方向:空中交通管理;通讯作者:宋斐(1989 -)男,山西太原人,硕士研究生。研究方向:空中交通管理
2014年民航安全能力建设资金项目,2015年学生科技活动基金 基金号:X2015-25
10.3969/j.issn.1001-8972.2016.09.009

