2219铝合金应力时效强度演变规律及其强化模型

湛利华，张姣，贾树峰(中南大学 机电工程学院，高性能复杂制造国家重点实验室，湖南 长沙，410083)

2219铝合金应力时效强度演变规律及其强化模型

湛利华，张姣，贾树峰
(中南大学 机电工程学院，高性能复杂制造国家重点实验室，湖南 长沙，410083)

在时效温度为175℃，时效时间为18 h时，开展不同应力水平(120~200 MPa)条件下的应力松弛时效与蠕变时效对比实验。建立应力松弛时效与蠕变时效强化模型，对强化模型进行验证与分析。研究结果表明：合金的屈服强度不仅受应力强化作用面积的影响，而且在时效初期阶段高应力作用对合金的屈服强度产生重要影响；在相同应力强化作用面积条件下，分别由应力松弛时效强化模型与蠕变时效强化模型计算的屈服强度增量差值与应力强化作用面积之间存在一定的线性关系，可以通过蠕变时效来预测应力松弛时效过程中合金强度的演变规律。

应力松弛时效；蠕变时效；力学性能；强化模型；2219铝合金

随着航空航天业的迅猛发展，针对复杂结构薄壁零件冷加工成形精度低、尺寸一致性差等难题，欧美等发达国家重点开展了应力松弛时效成形技术研究[1-3]，提出一种将应力松弛或蠕变与人工时效热处理相结合的新技术，并应用于航空航天大型带筋壁板成形制造中[4]。应力松弛时效与蠕变时效这2种应力时效方法都是利用材料的时效强化和蠕变松弛特性，在实现工件成形的同时，完成工件的时效强化，改善合金内部的微观组织特征，提高合金的强度。应力松弛时效是指材料在恒定的应变条件下，应力随时间而逐渐减小的现象；蠕变时效是指材料在恒定应力作用下，在应力作用时变形量缓慢增加的过程[5]。在应力松弛过程中增加的蠕变变形与蠕变时效过程中的蠕变现象都可以通过位错理论来解释[6]，可以说松弛是蠕变的另一种表现形式。RUDNICK等[7]认为材料在长期扭力作用下会发生应力松弛行为，这是因为存在蠕变行为；穆霞英[8]认为应力松弛是蠕变现象的另一种表现，是由于弹性变形转换为蠕变变形，引起应力相应减少。CHEN等[9]研究了蠕变时效成形过程中材料的应力松弛演变规律，并通过计算热激活参数和分析微观组织详细阐述了应力松弛的发生机制。这表明应力松弛行为与蠕变行为在机理上是统一的，两者之间应该存在转换关系。国内外学者对蠕变时效本构建模开展了大量研究，如：黄硕等[10-11]研究了在不同时效温度(145，155和165℃)、不同应力水平条件下7B04铝合金的多组单轴拉伸蠕变试验，根据蠕变变形特征提出了能够较好描述材料蠕变行为的本构模型，并通过对2324铝合金进行蠕变拉伸试验，对试验数据进行分析处理，建立了相应的蠕变本构方程；PEDDIESON等[12]建立了一维蠕变时效本构模型，分析了7075铝合金材料在时效温度为163℃的时效成形过程，并对构件的回弹进行了预测；JACKSON等[13]采用包含1个状态变量的更新MILLER-SHERBY统一黏塑性蠕变模型，对7075铝合金构件的回弹特性进行了分析，该模型忽略了热应力的影响。这些研究大多仅局限于建立蠕变时效过程的合金强化本构模型，对于应力松弛时效过程中合金强度的演变规律并没有描述。为此，本文作者通过进行不同应力水平条件下的应力松弛时效与蠕变时效对比实验，建立应力松弛时效与蠕变时效强化模型，并确定2个强化模型的关联规律。

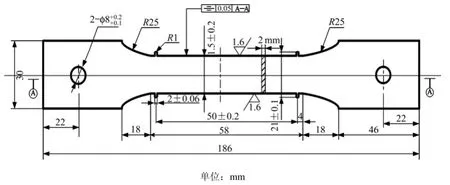
图1　试样尺寸Fig.1　Geometry dimension of specimen

1　实验材料与方法

1.1实验材料

2219铝合金是一种高强度、可热处理强化型铝合金，具有较高的比强度、较强的抗腐蚀性能以及较高塑性，被认为是航空航天工业中最具有应用前景的轻质高强结构材料之一，从而被广泛地应用于火箭推进器液体燃料贮箱制造中[14]。

本文研究所选用的材料为上海航天设备总厂提供的2219铝合金轧制板材，合金的主要化学成分(质量分数)如表1所示。按照 GB/T 2039—1997，沿轧制方向线切割出2 mm厚的标准蠕变试样，试样尺寸如图1所示。在电阻加热炉中进行固溶处理，固溶温度为535℃，保温35 min。采用电位差计控制炉温，误差控制在±3℃内；室温水淬，淬火转移时间少于35 s；固溶处理后立即进行应力松弛时效与蠕变时效实验。

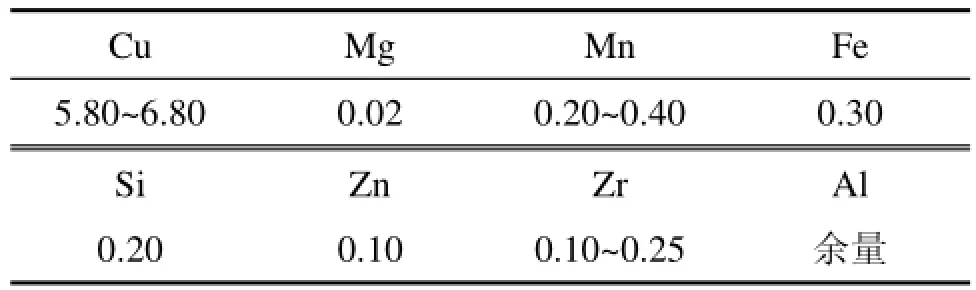
表1　2219铝合金化学成分(质量分数)Table 1　Chemical compositions of 2219 aluminum alloy %

1.2实验方法

2219铝合金蠕变时效与应力松弛时效实验在珠海市三思泰捷电气设备有限公司生产的RMT-D10电子式高温蠕变持久强度试验机上进行，试样平行于炉膛内部安装，3个热电偶结点紧贴在试样表面上，靠近热电偶结点处用石棉绳包裹。试样加热到175℃后保温10 min左右，然后平稳加载，加载速率为15 N/s，并随时调正杠杆，保持试件处于单向拉应力状态，整个实验过程由计算机控制。实验结束后，保存实验数据，取下试样，水平放置，空冷至室温。

在时效温度为175℃、时效时间为18 h时，分别进行不同应力(120~200 MPa)条件下的蠕变时效与应力松弛时效实验。在蠕变时效实验过程中，保持加载应力恒定。应力松弛时效实验分为3种加载方式：1)在不同初始加载应力(120~200 MPa)下，实验过程中保持应变恒定，直到实验结束；2)在时效初始阶段，由初始加载应力200 MPa分别松弛到180，160，140和120 MPa，然后保持恒应力，继续时效到实验结束；3)在时效初始阶段，由不同的初始加载应力(200，180，160和140MPa)分别松弛到120 MPa，然后保持恒应力，继续时效到实验结束。最后，将时效处理后的试样在万能力学试验机上进行力学性能测试。

2　实验结果与分析

在时效温度为175℃、时效时间为18 h和不同应力水平(120，140，160，180和200 MPa)时，经过恒应变应力松弛时效与恒应力蠕变时效处理后2219铝合金的力学性能如图2所示。

由图2可以看出：在不同应力水平条件下，恒应力蠕变时效处理后合金的强度随着试验应力的增加呈现先升高后降低的趋势，而恒应变应力松弛时效处理后合金的屈服强度随着试验应力的增大而增大。当应力为160 MPa时，合金经过恒应变应力松弛时效处理后的屈服强度为310.5 MPa，而经过恒应力蠕变时效处理后合金的屈服强度为317.1 MPa，提高了2.1%。这是由于恒应变的应力松弛时效过程中，在时效初始阶段，初始应力迅速降低，使得合金在低应力作用下进行时效，而在恒应力的蠕变时效过程中应力保持不变，所以强度较高。

图2　试验应力对合金屈服强度的影响Fig.2　Effect of experimental stresses on yield strength of 2219 aluminum alloy

通过研究恒应变应力松弛时效与恒应力蠕变时效对合金力学性能的不同影响，可以看出合金应力松弛时效过程初始阶段应力急速降低阶段对合金的性能产生重要的影响，所以需要对应力松弛阶段进行研究。

当时效温度为175℃、时效时间为18 h、初始加载应力为200 MPa、保持恒应变时，应力分别松弛到120，140，160和180 MPa，然后在保持恒应力的条件下继续时效，整个试验过程的时效时间为18 h；蠕变时效试验在时效温度为175℃，应力分别为120，140，160和180 MPa，在恒应力的条件下保温18 h。

初始加载应力200 MPa松弛到不同应力条件下的应力松弛时效处理与不同应力条件下蠕变时效处理后合金的力学性能如图3所示。

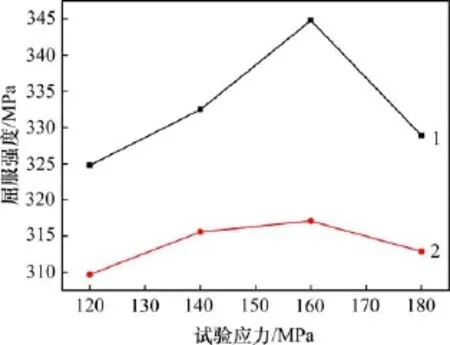
图3　蠕变时效与应力松弛时效力学性能对比Fig.3　Comparison of mechanical properties between creep age and stress relaxation age

从图3可以看出：在相同应力水平条件下，先经过恒应变应力松弛后进行恒应力蠕变时效处理的合金屈服强度要明显高于只进行恒应力蠕变时效处理后合金屈服强度，当应力为160 MPa时，只进行恒应力蠕变时效处理后合金的屈服强度为317.1 MPa，而先经过恒应变应力松弛后进行恒应力蠕变时效处理后合金的屈服强度为344.8 MPa，提高了8.7%。这是由于应力松弛第1阶段在高应力和温度的激活作用下，位错将产生攀移和滑移，一方面，异号位错相互抵消，另一方面，同号位错趋于能量最低的状态排列，产生加工硬化现象[15]，使得合金强度提高。

当时效温度为175℃、初始阶段保持恒应变时，将不同初始加载应力(120，140，160，180和200 MPa)分别松弛到120 MPa，然后在保持恒应力的条件下继续进行时效，整个时效过程的时间为18 h，应力松弛曲线如图4所示。

图4　不同初始加载应力条件下的应力松弛曲线Fig.4　Stress relaxation curves under different initial loading stresses

从图4可以看出：与120 MPa恒应力蠕变时效相比，在不同初始加载应力条件下，初始恒应变应力松弛阶段的应力较高。故合金先经过恒应变应力松弛时效，然后恒应力蠕变时效处理时，应力与时间作用的总面积要大于恒应力蠕变时效的总面积，从而可能对合金的力学性能产生影响。

当时效温度为175℃、时效时间为18 h时，合金在不同初始加载应力条件下，先经过恒应变应力松弛时效将应力松弛到120 MPa，然后恒应力蠕变时效处理后的力学性能如表2所示。

从表2可以看出：与恒应力蠕变时效处理后合金的屈服强度相比，合金在高应力作用下应力松弛时效一段时间，对时效初期析出相的析出产生了促进作用，使得合金的屈服强度明显提高。

通过对比分析图4及表2中应力对合金力学性能的影响，发现在合金时效初期，应力松弛时效和蠕变时效对2219铝合金性能的影响规律不一致，且初始应力及应力强化的总作用面积共同影响着合金屈服强度的提高，所以，直接通过蠕变时效试验得出的蠕变时效强化模型来预测应力松弛(实际工况)试验的强度演变规律存在不合理性，需要建立基于应力强化作用面积的合金应力松弛时效强化模型与蠕变时效强化模型，研究应力松弛时效与蠕变时效对合金屈服强度影响的关联规律。

表2　不同初始加载应力条件下应力松弛时效2219铝合金力学性能Table 2　Mechanical properties of 2219 aluminum alloy after stress relaxation age under different initial loading stresses

3　应力松弛时效与蠕变时效强化模型的建立

3.1应力松弛时效强化模型的建立

当时效温度为175℃、时效时间为18 h、不同初始加载应力(120，140，160，180和200 MPa)条件下，合金应力松弛时效实验结果及拟合曲线如图5所示。

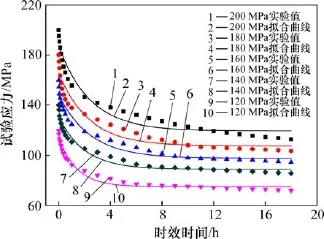
图5　应力松弛实验数据与拟合曲线Fig.5　Experimental data of stress relaxation age and fitting curves

据图5中不同初始加载应力条件下的应力松弛实验数据点的分布特点，可以建立如下应力松弛模型[16]：

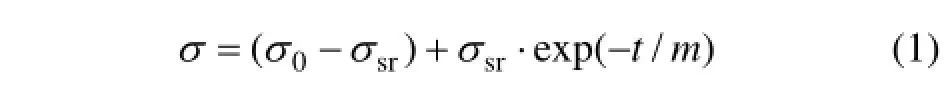
式中：σ为试验应力；0σ为加载应力；srσ 为应力松弛量；m为材料常数。通过Origin软件进行数据拟合，得到应力松弛模型中的参数如表3所示。

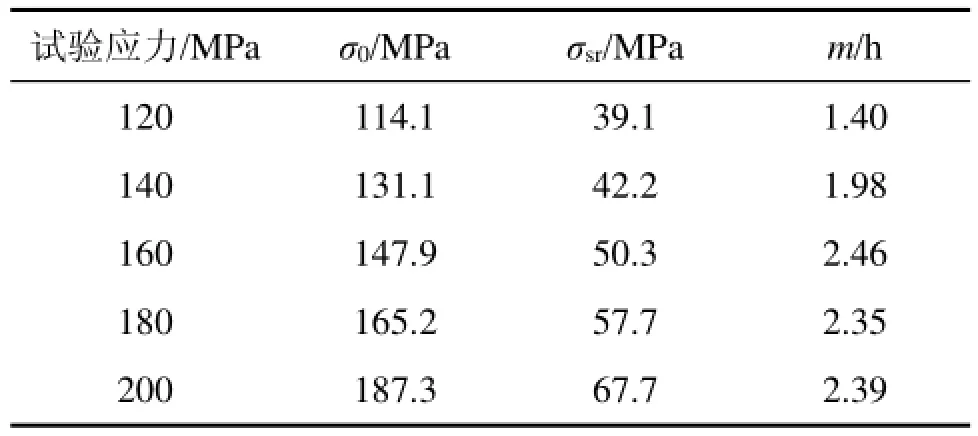
表3　应力松弛曲线方程参数Table 3　Material parameters of stress relaxation model

通过应力松弛曲线方程，则可以计算出不同应力水平条件下的应力强化作用面积A：

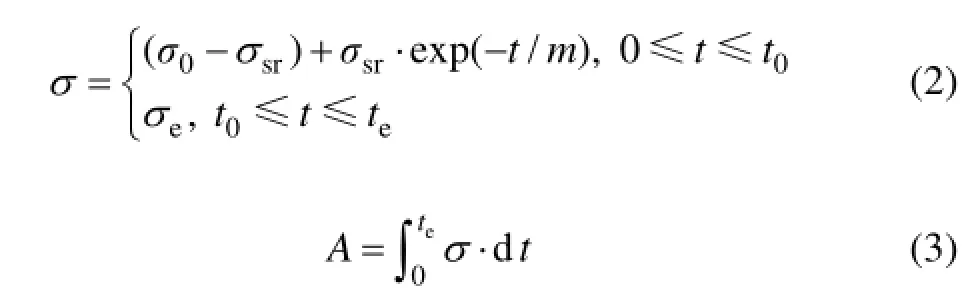
式中：eσ为恒应力蠕变时效试验应力；t0为应力松弛阶段结束时间；te为实验过程总的时效时间。从力学性能测试结果可以看出：当峰值应力作用面积Ap= 2 891 MPa·h时，合金的最大屈服强度增量 dys= 47.3 MPa。若继续增大应力强化作用面积，则合金的屈服强度增量开始降低。这可能是由于合金在此阶段已经进入过时效阶段，导致合金的性能降低。当应力作用面积小于Ap时，合金的屈服强度增量与应力作用面积近似呈线性变化关系(见图6)。可以建立2219铝合金应力松弛时效强化模型：

式中：dys为合金屈服强度增量；k和B为材料常数。通过Origin软件将数据进行拟合，强化模型中的材料常数如下：k为0.036 h-1，B为-55.4 MPa，判定系数R2为98.7%。合金屈服强度增量与应力强化作用面积之间的拟合关系如图6所示。

3.2蠕变时效强化模型的建立

开展不同应力条件下的蠕变时效实验，然后进行力学性能测试，得到蠕变时效处理后合金的屈服强度增量随应力强化作用面积的变化关系。蠕变时效应力强化作用面积可通过恒应力与时效时间所围成的面积计算所得，建立蠕变时效强化模型。当时效温度为175℃、时效时间为18 h时，合金的屈服强度增量与应力强化作用面积的关系如图7所示。

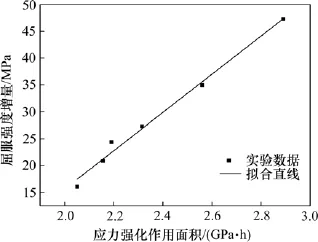
图6　应力松驰时效屈服强度增量与应力强化作用面积拟合曲线Fig.6　Data fitting curve for yield strength increment stress relaxation age under different stress reinforcement areas

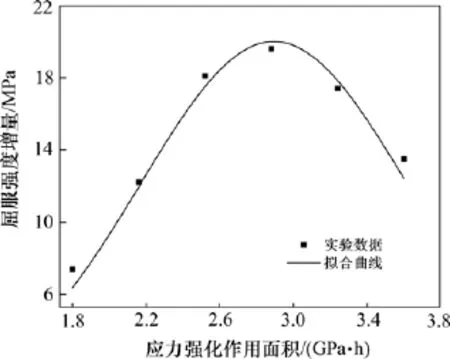
图7　蠕变时效屈服强度增量与应力强化作用面积拟合曲线Fig.7　Data fitting curve for yield strength increment of creep age under different stress reinforcement areas

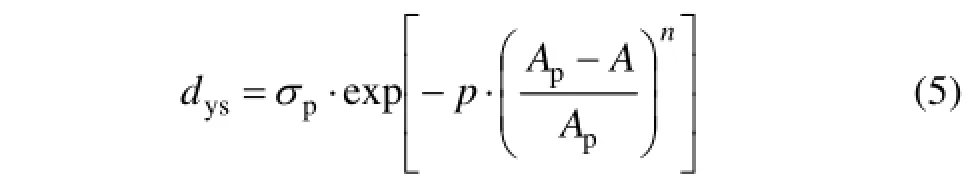
图7中，黑色方形点为不同应力强化作用面积所对应的合金屈服强度增量实验值，曲线为通过实验数据所拟合的曲线。从图7可以看出：随着应力强化作用面积的增大，合金屈服强度增量呈现先升高后降低的趋势。合金蠕变时效强化模型为式中：pσ为峰值强化作用面积所对应的屈服强度增量；Ap为峰值应力强化作用面积；A为应力强化作用面积；p和n为材料常数。通过Origin软件进行数据拟合，得到强化模型中的材料参数：Ap为2 893.5 MPa·h；pσ为20 MPa；p为8；n为2；判定系数R2为92.8%

3.3应力松弛与蠕变时效强化模型关联规律的确定

在时效过程中，合金屈服强度增量不仅与应力强化作用面积有关，而且初始加载应力及作用时间也对合金的屈服强度产生重要影响。时效初期是合金强化的重要阶段，所以，在时效初期，高应力作用会加速合金内析出强化相的析出，使得合金的强度得到较大提高。通过建立的应力松弛时效强化模型与蠕变时效强化模型，分别求出在相同应力强化作用面积下2个强化模型所对应的屈服强度增量，发现在相同应力强化作用面积条件下，由应力松弛时效强化模型计算的屈服强度增量要高于由蠕变时效强化模型计算的屈服强度增量。在相同应力强化作用面积条件下，分别由应力松弛时效强化模型与蠕变时效强化模型计算的屈服强度增量差值与应力强化作用面积存在一定线性关系，如图8所示。

图8　屈服强度增量差值与应力强化作用面积线性拟合曲线Fig.8　Linear fitting curve between incremental difference of yield strength and reinforcement area of stress

通过Origin软件进行数据拟合，得到屈服强度增量差值与应力强化作用面积的线性拟合方程为

式中：R为合金屈服强度增量差值；l和q为材料常数。所得屈服强度增量差值模型参数如下：l为0.022 h-1；q为-38.1 MPa；判定系数R2为99.2%。通过该模型建立恒应力蠕变时效与恒应变应力松弛时效强化模型之间的关系，从而可以通过进行恒应力蠕变时效来预测恒应变应力松弛时效过程中合金强度的演变规律。

4　结论

1)应力松弛时效和蠕变时效对2219铝合金性能的影响规律不一致：当试验应力为160 MPa时，应力松弛时效处理后合金的屈服强度为310.5 MPa，而蠕变时效处理后合金的屈服强度为317.1 MPa；先进行恒应变应力松弛时效后进行恒应力蠕变时效处理后合金的区服强度为344.8 MPa。

2)合金的屈服强度不仅受应力强化作用面积的影响，而且在时效初期阶段，高应力作用会对合金的屈服强度产生重要影响。

3)建立了2219铝合金蠕变时效强化模型和应力松弛时效强化模型，通过对强化模型的验证与分析，发现在相同应力强化作用面积条件下，由2个强化模型计算的屈服强度增量差值与应力强化作用面积呈线性关系。因此，可以通过进行恒应力蠕变时效来预测应力松弛时效过程中合金强度的演变规律。

[1]曾元松,黄遐,黄硕.蠕变时效成形技术研究现状与发展趋势[J].塑性工程学报,2008,15(3):1-8. ZENG Yuansong,HUANG Xia,HUANG Shuo.The research situation and the developing tendency of creep age forming technology[J].Journal of Plasticity Engineering,2008,15(3): 1-8.

[2]常荣福.飞机钣金零件制造技术[M].北京:国防工业出版社, 1992:110-111. CHANG Rongfu.Aircraft sheet metal parts manufacturing technology[M].Beijing:National Defence Industry Press,1992: 110-111.

[3]韩志仁,戴良景,张凌云.飞机大型蒙皮和壁板制造技术现状综述[J].航空制造技术,2009(4):64-66. HAN Zhiren,DAI Liangjing,ZHANG Lingyun.Current status of large aircraft skin and panel manufacturing technologies[J]. Aeronautical Manufacturing Technology,2009(4):64-66.

[4]IDEM K,PEDDIESON J.Simulation of the age forming process[J].Journal of Manufacturing Science and Engineering, 2005,127(1):165-172.

[5]黄晓婧,王俊彪,张贤杰.铝合金时效蠕变与时效应力松弛关系研究[J].航空制造技术,2011(11):99-101. HUANG Xiaojing,WANG Junbiao,ZHANG Xianjie.Researchon relationship between aging creep and stress relaxation of Al-alloy[J].Aeronautical Manufacturing Technology,2011(11): 99-101.

[6]阳志安.位错蠕变理论的现状和发展[J].材料科学与工程学报,1987(3):26-32. YANG Zhian.The status and development of dislocation creep theory[J].Journal of Materials Science and Engineering,1987(3): 26-32.

[7]RUDNICK A,HUNTER A R,HOLDEN F C.An analysis of the diametral-compression test[J].Mater Res Stand,1963,3(4): 283-289.

[8]穆霞英.蠕变力学[M].西安:西安交通大学出版社,1990: 6-7. MU Xiaying.Creep mechanics[M].Xi’an:Xi’an Jiaotong University Press,1990:6-7.

[9]CHEN J F,JIANG J T,ZHEN L,et al.Stress relaxation behavior of an Al-Zn-Mg-Cu alloy in simulated age-forming process[J]. Journal of Materials Processing Technology,2014,214(4): 775-783.

[10]黄硕,万敏,黄霖,等.铝合金蠕变试验及本构模型建立[J].航空材料学报,2008,28(1):93-95. HUANG Shuo,WAN Min,HUANG Lin,et al.Aluminum alloy creeptestanditsconstitutivemodeling[J].Journalof Aeronautical Materials,2008,28(1):93-95.

[11]黄硕,曾元松,黄遐.2324铝合金蠕变时效成形有限元分析[J].塑性工程学报,2009,16(4):129-133. HUANG Shuo,ZENG Yuansong,HUANG Xia.FE analysis of creep age forming for aluminum alloy 2324[J].Journal of Plasticity Engineering,2009,16(4):129-133.

[12]PEDDIESON J J,GEORGE R B.Mathematical modeling of an age-forming process[J].Mathematical and Computer Modeling, 1990,14:1057-1060.

[13]JACKSONMJ,PEDDIESONJ,FOROUDASTANS. Age-forming of beam structures-analysis of springback using a unified viscoplastic model[J].Journal of Materials:Design and Applications,2005,219(1):17-24.

[14]孟庆国,方洪渊,徐文立,等.2219铝合金双丝焊热影响区组织及力学性能[J].焊接学报,2006,27(3):9-12. MENGQingguo,FANGHongyuan,XUWenli,etal. Microstructure and mechanical properties of 2219 Al-alloy heat affected zone with twin wire welding[J].Transactions of the China Welding Institution,2006,27(3):9-12.

[15]张新明,毛新平,邓至谦,等.铍铜带材弯曲应力松弛的力学行为[J].中国有色金属学报,2001,11(6):988-992. ZHANG Xinming,MAO Xinping,DENG Zhiqian,et al.Stress relaxation characteristics in bending of Cu-Be alloys[J].The Chinese Journal of Nonferrous Metals,2001,11(6):988-992.

[16]金尧,魏楠.金属高温应力松弛行为研究[J].机械强度,1997, 19(3):57-60. JIN Yao,WEI Nan.Research on stress relaxation of metals at elevated temperature[J].Journal of Mechanical Strength,1997, 19(3):57-60.

(编辑陈灿华)

Strength evolution rule and its model for stress aging of 2219 aluminum alloy

ZHAN Lihua,ZHANG Jiao,JIAShufeng
(State Key Laboratory of High Performance Complex Manufacturing,School of Mechanical and Electrical Engineering, Central South University,Changsha 410083,China)

The comparison experiment of stress relaxation aging and creep aging was carried out under the stress of 120-200 MPa at 175℃ aging for 18 h.The strength model of both stress relaxation aging and creep aging was established.The results show that the yield strength is affected not only by the reinforcement area of stress,but also by the high stress at the beginning of the aging stage through the test of mechanical properties.A linear relationship is found between the incremental difference of yield strength calculated based on the strength model of stress relaxation aging and creep aging under the condition of the same stress reinforcement area.So the evolution rule of strength during stress relaxation aging can be predicted by conducting the experiment of creep aging.

stress relaxation aging;creep aging;mechanical properties;strength model;2219 aluminum alloy

湛利华，教授，从事铝合金蠕变时效研究；E-mail:yjs-cast@csu.edu.cn

TG146.2

A

1672-7207(2016)07-2235-07

10.11817/j.issn.1672-7207.2016.07.008

2015-07-20；

2015-08-24

国家重点基础研究发展计划(973计划)项目(2014CB046602)；国家自然科学基金重点资助项目(51235010)；国家教育部博士点基金资助项目(20120162110003)(Project(2014CB046602)supported by the National Basic Research Development Program(973 Program)ofChina;Project(51235010)supportedbytheKeyProgramoftheNationalNaturalScienceFoundationofChina; Project(20120162110003)supported by the PhD Programs Foundation of Ministry of Education of China)