三维接触面单元弹塑性损伤数值模拟分析方法

邓建，肖明，谢冰冰(1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉，430072；2.武汉大学 水工岩石力学教育部重点实验室，湖北 武汉，430072)

三维接触面单元弹塑性损伤数值模拟分析方法

邓建1,2，肖明1,2，谢冰冰1,2
(1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉，430072；
2.武汉大学 水工岩石力学教育部重点实验室，湖北 武汉，430072)

针对岩土工程中出现的非连续结构面、接触面等问题，建立一种新的模拟结构面或接触问题的三维非线性接触单元模型；针对接触面非线性变形以及损伤演化特性，提出一种可以考虑接触面损伤演化过程的弹塑性损伤数值模拟方法；针对接触面张开、闭合以及剪切滑移失效等变形特性，模拟接触面的黏结、滑移和开裂等非线性现象。针对某水电站地下厂房岩锚吊车梁围岩与混凝土接触问题进行数值分析。研究结果表明：采用接触面单元模拟混凝土结构与围岩的相互作用，吊车梁受力情况良好，应力、变形分布正常，基本规律与实际相符，在工程实践中是合理可行的。

岩土工程；非线性；接触单元；弹塑性；损伤演化；数值模拟

在岩土结构工程中，存在着大量接触问题，如岩体的结构面、混凝土结构的分缝以及结构与基础、不同材料的交界面等[1]。这些接触面表现出不同于一般岩体的力学特性，即在荷载作用下，可能发生张开、滑移、闭合等现象[2]，对结构的安全稳定有较大影响，因此越来越受到人们的重视。长期以来，许多中外学者对接触问题进行了多方面研究，先后基于不同的理论提出了各种接触面计算模型。GOODMAN等[3]基于弹簧刚度提出了用于模拟节理岩体的无厚度接触面单元，得到了广泛应用，其主要问题是弹簧刚度系数选取的任意性及其合理取值的困难性。DESAI等[4]提出了有厚度的非线性薄层单元，在一定程度上克服了GOODMAN接触面单元的缺点，其界面参数包括弹性模量E、剪切模量G、泊松比γ这3个参数，但在参数取值方面缺乏理论依据。BOULON等[5]提出了接触面弹塑性模型，但是由于较复杂而未能得到推广应用。CLOUGH等[6]在实验基础上提出了非线性弹性模型。武亚军等[7]将非线性弹性理论与弹塑性理论相结合，提出了一种非线性弹性-理想塑性本构模型。张冬霁等[8]在实验基础上提出了剪切错动带单元。卢廷浩等[9]基于剪切错动带提出了接触面法向刚度与切向刚度相耦合的非线性本构模型。高俊合等[10]通过大型单剪实验提出了有厚度剪切滑移薄层单元。胡黎明等[11]进行了系统的土与结构物接触面的直剪试验,根据试验结果建立了描述接触面应变软化和剪胀现象的损伤力学模型。安关峰等[12]提出了接触面的三维弹-粘-塑性模型。本文作者在以上研究的基础上，提出了一种具有滑移失效及拉伸、剪切、黏结特性的三维接触面弹塑性损伤有限元计算方法，并通过工程实例验证该方法的合理性。

1　接触面单元基本模型

图1所示为接触面单元模型。考虑图1中三维8节点等厚度接触单元，沿法向zˊ方向分为上、下2平面，接触单元厚度为t，t/ b=1/100～1/10，b为接触单元的长度。形函数满足

在有限元计算中，整体坐标与接触面的局部坐标往往是不一致的，在三维坐标系中，由Oxyz转换到Oˊxˊyˊzˊ坐标系时，其坐标转换矩阵[R]可表示为

图1　接触面单元模型Fig.1　Contact element model

假设薄层单元沿厚度方向即法向zˊ方向应变均匀分布，以接触面单元对应点的相对位移表征单元的应力应变[13]，其相对位移为

则接触面上表面任意一点的相对位移为：

则单元应变为：

若接触面单元的应力矩阵为[D]，则根据虚位移原理，有

考虑到厚度t尽可能小，接触面单元整体刚度矩阵可表示为

2　接触面单元弹塑性本构

接触面单元在复杂外荷载作用下其应力应变关系常表现出一定的非线性，在发生剪切变形和受高压应力作用时，可能产生沿粗糙体表面的滑移以及粗糙体剪断、压碎和磨损、拉裂等现象，接触面单元的变形中不仅有可逆的弹性变形，而且有不可逆的塑性变形，本文采用接触面单元弹塑性本构模型进行数值模拟[14-15]。

根据弹塑性理论，当空间某一点的应力状态进入屈服后，其应力应变关系表现为非线性，此时应变增量可分解为弹性应变增量和塑性应变增量两部分，即

其中：弹性部分满足虎克定律，塑性部分满足塑性流动法则，即

式中：F为屈服函数。

对于弹性部分，忽略法向和切向变形的耦合影响，只考虑接触面单元法向和切向的单独承载响应，采用弹性应力矩阵：

对于塑性部分，采用下述混合准则：当接触面产生剪切破坏时，采用Mohr-Coulomb准则；当接触面产生受拉破坏时，因为其抗拉强度低，承受法向拉应力时，容易开裂，所以，受拉破坏的强度条件采用最大拉应力准则，即

根据变形相容条件，有

式中：F为屈服函数，H为硬化参数。可得 λd为

对于弹塑性应力增量则可以表示为

其中，塑性应力矩阵可表示为

3　接触面单元损伤开裂模拟

3.1接触面损伤塑性模型

在外荷载作用下，接触面除了表现出非线性变形特性外，还会逐渐产生微裂纹和微孔隙等损伤破坏情况，损伤的发生和积累导致结构材料刚度劣化和强度降低。为了模拟这种随着塑性变形的产生、积累而形成的损伤演化过程，本文在弹塑性本构模型的基础上，通过引入损伤变量[16]，建立了接触面单元弹塑性损伤本构模型。

在承载过程中，由于出现新的损伤，并出现新的塑性变形，应变增量可分解为3部分：

d{ε}d和d{ε}p分别是损伤应变和塑性应变增量，其满足广义正交法则：

引入损伤变量ω，则损伤应变增量可以定义如下：

假设接触面的损伤变形和塑性变形是同时出现的，当应力状态满足屈服准则F(σ, ω)=0时,才有可能出现新的损伤变形和塑性变形。

在不考虑黏性效应的情况下，可以假定损伤变量增量dω与塑性应变增量之间满足以下关系：

式中：Tn是一个三维矢量，它是损伤变量ω和单元应力σ的函数。通过式(21)~(23)可得

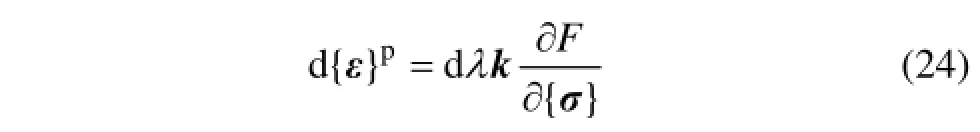
采用与不考虑损伤劣化相同的本构矩阵形式，即式(18)所示，其中H可以表示为

10月24日，“经协”筹备会召开座谈会，提出经济民主的九点主张，并于11月5日在《商务日报》上发表。这年冬，“经协”筹备会举行欢迎中共代表团的小型集会。周恩来、邓颖超、陆定一等参加，周恩来讲了话。这次会议对“经协”筹备会的负责人鼓舞很大。

式中：矩阵[D]和硬化参数H均含有损伤变量ω。再由式(9)和式(10)计算接触面单元刚度矩阵。

3.2接触面破坏状态模拟

由于接触面单元在平行和垂直于接触面方向分别表现出不同的物理力学特性，所以，在弹塑性非线性分析时，应对平行于接触面和垂直于接触面2个方向的破坏特性进行判断。

3.2.1拉裂破坏

对垂直于接触面的破坏情况，先计算接触面单元局部坐标下的应力：

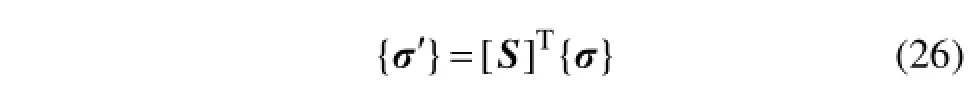
[S]为应力转化矩阵。然后根据局部坐标下的应力分量校核垂直于接触面的正应力状态，当

说明垂直接触面的正应力超过极限抗拉强度Rt，垂直于接触面方向将开裂。此时必须将超出接触面抗拉强度的应力转化成节点荷载，并将其转移。对于发生拉裂破坏的单元，抗拉强度Rt设置为零，单元不再进行损伤处理，直接标记为分离状态。

对平行于接触面的破坏情况，应校核是否沿接触面滑移。当接触面单元的应力状态满足

式中：f为接触面的摩擦系数；c为黏结力；k为接触面滑动安全系数。此时平行于接触面方向将产生剪切滑动，同时应将超出抗剪强度的剪力：

转化成节点荷载，并将其转移。对于发生剪切破坏的单元，则把单元标记为滑移状态，抗拉强度Rt修正为残余强度。

3.2.3拉裂破坏后闭合

再接触状态是指已经拉裂破坏的接触单元再次受压时会产生闭合，恢复为接触状态，在力学性质上表现为法向刚度和切向刚度的恢复。再接触状态判断可以采用如下方法：

如果单元法向位移满足上式，那么单元处于再接触状态，抗拉强度Rt同样设置为0 MPa。

4　工程实例

4.1工程概况黄登水电站位于云南省怒江州兰坪县境内，为澜沧江上游河段规划中的第5个梯级，引水发电系统位于枢纽左岸，主要建筑物有主副厂房、主变室、尾水调压井等3大洞室及电站进水口、压力管道、机组尾水检修闸门室、尾水隧洞及其他相关辅助洞室。整个厂区洞室纵横交错规模宏大，属大型地下洞室群。其中引水隧洞(包括钢管段)共4条，平行布置，中心间距为31 m，单条隧洞长244.54 m；主副厂房开挖长× 宽×高为228.0 m×30.3 m×76.5 m；主变室开挖长× 宽×高为153 m×18 m×30 m；尾水调压井采用圆筒阻抗式，内径为26 m，高为73 m，阻抗孔直径为8.5 m；调压井后接两条尾水隧洞，1号隧洞长度为422.092 m，隧洞长度为323.339 m，洞径为15 m。

4.2计算模型和计算条件

建立吊车梁局部细化模型进行计算分析。综合分析本工程的地形、地质特性，取2号机组段进行岩锚吊车梁的稳定分析，模型包括2号机组段的主厂房、引水管、母线洞、主变洞、尾水管等。模型全部采用八节点六面体单元进行离散，共剖分了70 496个单元和74 978个节点。其中浇筑混凝土单元11 200个，接触单元1 120个。三维有限元模型开挖单元如图2所示，岩锚吊车梁混凝土单元及接触单元模型如图3所示。

图2　三维有限元模型Fig.2　Three-dimensional finite element model

图3　混凝土及接触单元模型Fig.3　Concrete and contact element model

初始地应力场通过实测地应力反演获得，属中等略低地应力。地下厂房区域岩体条件较好，以Ⅱ和Ⅲ类围岩为主，材料力学参数取值如表1所示。

表1　材料力学参数取值Table 1　Mechanical parameters of materials

计算工况：1)采用等效连续模型分析洞室群开挖对吊车梁混凝土受力影响；2)采用接触面单元模型分析洞室群开挖对吊车梁混凝土受力影响。

4.3计算结果分析

为了论证接触面单元弹塑性损伤数值模拟分析方法的合理性，本文分别采用等效连续模型和接触面单元模型进行数值模拟，选取吊车梁机组段典型断面，对比分析地下厂房开挖完毕岩锚吊车梁混凝土应力和变形分布规律。

4.3.1岩锚吊车梁应力分布规律

分别采用等效连续模型和接触面单元模型进行数值模拟，厂房开挖完毕后岩锚吊车梁第1、第3主应力(拉为正，压为负)如图4~7所示。

采用等效连续模型进行分析计算(见图4和图5)，开挖完毕吊车梁混凝土第1主应力分布在-0.07~-2.52 MPa之间，第3主应力分布在-0.31~1.81 MPa之间。从图4和图5可以看出：第1主应力不大，但第3主应力局部超过混凝土的抗拉强度，发生局部开裂。

图4　等效连续模型第1主应力Fig.4 The 1st principle stress with equivalent continuum model

采用接触面单元模型进行分析计算(见图6和图7)，开挖完毕吊车梁混凝土第1主应力分布在-0.05~ -1.31 MPa之间，第3主应力分布在-0.10~1.13 MPa之间。从图6和图7可以看出：吊车梁混凝土应力值较小，第3主应力均小于混凝土的抗拉强度。

图5　等效连续模型第3主应力Fig.5　The 3rd principle stress with equivalent continuum model

图6　接触面单元模型第1主应力Fig.6　The 1st principle stress with contact element model

图7　接触面单元模型第三主应力Fig.7　The 3rd principle stress with contact element model

从图6和图7可以看出：采用接触面单元模拟吊车梁混凝土与围岩的接触状态，吊车梁受力情况良好，应力分布均匀，能够有效控制后期开挖对吊车梁的扰动影响，且与工程实际更为吻合。

4.3.2岩锚吊车梁变形分布规律

分别采用等效连续模型和接触面单元模型进行数值模拟，厂房开挖完毕岩锚吊车梁位移分布如图8和图9所示。

图8　等效连续模型位移分布Fig.8　Displacements distribution with equivalent continuum model

图9　接触面单元模型位移分布Fig.9　Displacements distribution with contact element model

采用等效连续模型进行分析计算(见图8)，厂房开挖完毕时，吊车梁变形在11.5~12.1 mm之间，最大变形量出现在吊车梁自由面，接触面部位位移从上到下逐渐增大。吊车梁上下游位移和分布规律均相似，基本以厂房中心线呈对称分布。总体来看，吊车梁下部区域岩体和母线洞岩体开挖对吊车梁影响较大。

采用接触面单元模型进行分析计算(见图9)，厂房开挖完毕时，吊车梁变形在7.6~8.8 mm之间，吊车梁变形均匀，变形较小，上下游位移和分布规律基本一致。

从图8和图9可以看出：采用接触面单元模拟吊车梁混凝土与围岩的接触状态，吊车梁受力良好，变形规律正常，以随围岩整体变形为主，变形量减小约3 mm，更加符合工程实际，有一定的模拟效果。

5　结论

1)基于Desai薄层单元的基本理论，建立了一种新的模拟接触问题的三维非线性接触单元模型，并基于非线性损伤演化基本理论，提出了接触面单元弹塑性损伤开裂模型。

2)采用接触面单元模拟混凝土结构与围岩的相互作用，吊车梁受力情况良好，应力、变形分布正常，基本规律与实际相符，在工程实践中是合理可行的，并为岩土工程非连续性接触问题的模拟提供了一种有效的分析方法。

[1]张楚汉.论岩石、混凝土离散-接触-断裂分析[J].岩石力学与工程学报,2008,27(2):217-220. ZHANG Chuhan.Discrete-contact-fracture analysis of rock and concrete[J].ChineseJournalofRockMechanicsand Engineering,2008,27(2):217-220.

[2]金峰,邵伟,张立翔,等.模拟软弱夹层动力特性的薄层单元及其工程应用[J].工程力学,2002,19(2):36-37. JIN Fen,SHAO Wei,ZHANG Lixiang,et al.A thin-layer element for simulation of static and dynamic characteristics of soft interlayer and its application[J].Engineering Mechanics, 2002,19(2):36-37.

[3]GOODMAN R E,TAYLOR R L,BREKKE T L.A model for the mechanics of jointed rock[J].Journal of Soil Mechanics and Foundation Engineering Division,1968,94(3):637-660.

[4]DESAI C S,ZAMAN M M,LIGHTNER J G,et al.Thin-layer element for interfaces and joints[J].International Journal for Numerical and Analytical Methods in Geomechanics,1984,8(1): 19-43.

[5]BOULON M,NOVA R.Modeling of soil structure interface behavior:a comparison between elastoplastic and rate-type laws[J].Computers and Geotechnics,1990,17(9):21-46.

[6]CLOUGH G W,DUNCAN J M.Finite element analysis of retaining wall behavior[J].Journal of Soil Mechanics and Foundation Engineering Division,1971,97(12):1657-1673.

[7]武亚军,栾茂田,杨敏.土与结构间一种新的接触单元模型[J].同济大学学报(自然科学版),2005,33(4):432-435. WU Yajun,LUAN Maotian,YANG Ming.New contact element of interface between soil and structure[J].Journal of Tongji University(Natural Science),2005,33(4):432-435.

[8]张冬霁,卢廷浩.一种土与结构接触面模型的建立及其应用[J].岩土工程学报,1998,20(6):62-66. ZHANG Dongji,LU Tinghao.Establishment and application of an interface model between soil and structure[J].Chinese Journal of Geotechnical Engineering,1998,20(6):62-66.

[9]卢廷浩,鲍伏波.接触面薄层单元耦合本构模型[J].水利学报,2000(2):71-75. LU Tinghao,BAO Fubo.A coupled constitutive model for interface thin layer element[J].Journal of Hydraulic Engineering, 2000(2):71-75.

[10]高俊合,于海学,赵维炳,等.土与混凝土接触面特性的大型单剪试验研究及数值模拟[J].土木工程学报,2000,33(4): 42-46. GAO Junhe,YU Haixue,ZHAO Weibing,et al.Characteristics of interface between soil and concrete by using large size single shearapparatusandnumericalanalysis[J].ChinaCivil Engineering Journal,2000,33(4):42-46.

[11]胡黎明,濮家骝.土与结构物接触面损伤本构模型[J].岩土力学,2002,23(1):6-11. HULiming,PUJialiu.Damagemodelofsoil-structure interface[J].Rock and Soil Mechanics,2002,23(1):6-11.

[12]安关峰,高大钊.接触面弹粘塑性本构关系研究[J].土木工程学报,2001,34(1):88-91. AN Guanfeng,GAO Dazhao.Research on elastic-visco-plastic constitution of interfaces[J].China Civil Engineering Journal, 2001,34(1):88-91.

[13]SAMADHIYA N K,VILADKAR M N,AL-OBAYDI M A. Three-dimensional joint/interface element for rough undulating major discontinuities in rock masses[J].International Journal of Geomechanics,2008,8(6):328-331.

[14]WANG J G,ICHIKAWA Y,LEUNG C F.A constitutive model for rock interfaces and joints[J].International Journal of Rock Mechanics and Mining Sciences,2003,40(1):41-53.

[15]肖明.地下洞室围岩稳定与支护数值方法研究[D].武汉:武汉大学水利水电学院,2002:56-61. XIAO Ming.Study on numerical analysis method of stability and supporting for underground caverns[D].Wuhan:Wuhan University.SchoolofWaterResourcesandHydropower Engineering,2002:56-61.

[16]殷有泉.考虑损伤的节理本构模型[J].工程地质学报,1994, 2(4):2-4. YIN Youquan.Joint constitutive model considering damage[J]. Journal of Engineering Geology,1994,2(4):2-4.

(编辑罗金花)

Three-dimensional elastic-plastic damage numerical simulation and analysis method for contact elements

DENG Jian1,2,XIAO Ming1,2,XIE Bingbing1,2
(1.State Key Laboratory of Water Resources and Hydropower Engineering Science,Wuhan University, Wuhan 430072,China;
2.Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of Ministry of Education, Wuhan University,Wuhan 430072,China)

In light of discontinuous joints and interfaces in geotechnical engineering,a new three-dimensional nonlinear contact element model for the simulation of joints and contact problems was presented.Based on the nonlinear deformation and damage evolution characteristics of contact elements,an elastic-plastic damage numerical simulation method which takes the damage evolution process into consideration was proposed.In view of the deformation characteristics of contact elements such as opening,closing and shearing slip damage,some nonlinear phenomena like bonding,slip and cracking were simulated.The contact problem between surrounding rocks and concrete crane beam of underground powerhouse was taken as an example.The results show that concrete crane beam is of better stress condition and normal deformation distribution with the contact element model,and the basic laws conform to the actual situation, which verifies the good rationality and accuracy of the present model in engineering practice.

geotechnical engineering;nonlinear;contact elements;elastic-plastic;damage evolution;numerical simulation

邓建，博士研究生，从事地下结构稳定数值分析研究；E-mail:xianyudj@126.com

TU45

A

1672-7207(2016)07-2383-07

10.11817/j.issn.1672-7207.2016.07.028

2015-07-23；

2015-09-23

国家自然科学基金重大资助项目(91215301)；国家自然科学基金资助项目(51279136,51209164)(Project(91215301) supported by the Major Program of National Natural Science Foundation of China;Projects(51279136,51209164)supported by National Natural Science Foundation of China)