宏程序编程新教学思路的运用

林万里华东石油技师学院

宏程序编程新教学思路的运用

林万里
华东石油技师学院

目前在数控车高级工技能鉴定或数控技能比赛中，经常出现宏程序编程的应用，这些内容在很多书籍和文章中也讲解的较多，但如何在实际教学中让我们的学生能够尽快理解和掌握其编程的方法，这是我们作为数控教师所面临的问题，本文将根据本人多年的教学总结，以椭圆为例对数控车宏程序编程的关键难点的新教学思路进行介绍。

数控车；宏程序编程；新教学思路

一、引言

宏程序的编程应该说对于目前经常接触数控编程的人来说，可能都会觉得这是个老生常谈的事情了，实际编程加工也不会给我们造成多大的困难，但是对于我们技工院校的学生来说，特别是初中毕业就读五年制的学生来说，他们毕业之前要面临高级工的技能鉴定，由于其数学底子薄弱，因此宏程序的编程对它们来说是一个很大的难点。而往往它们所面临的难点主要表现在：曲线拟合原理不容易理解；自变量的选择不合理；如何把标准曲线方程坐标系中的宏程序转换成工件坐标系中的宏程序，尤其第三个问题更为突出，那么如何在教学中让学生更好的理解并掌握宏程序编程的技巧与方法，下面以高级工技能鉴定典型零件（如图1）为例进行讲解，谈一谈FANUC系统中宏程序编程的教学思路。

二、宏程序编程的原理和其中存在的关键难题

1.宏程序编程的核心思想和理念

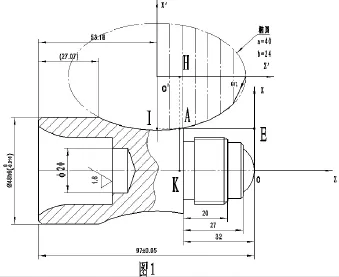
由于一般的数控机床系统中并没有提供椭圆曲线加工插补指令功能,因此如果要加工非圆曲线轮廓,只能利用微积分的理念将非圆曲线的沿着某一个坐标方向分若干等份点,通过非圆曲线的函数关系就能求出对应于每一等分点的另一坐标值,这样在理想的非圆曲线上就找到若干个点,即节点,每相邻两点之间近似看作一直线，然后利用G01的直线插补指令以刀具的进给方向将节点按顺序连接起来,这种方法称为拟合（如图1所示）。但近似的拟合曲线与理想的非圆曲线间存在一定误差,若其最终误差大于零件形状精度的要求,则就不能达到我们的加工要求。为能保证在形状上接近理想曲线轮廓,可将Z轴方向的等分点的数量增多,对应椭圆函数关系求得的节点数目也将随之增多,这样拟合出的直线段就将趋近于理想的椭圆曲线,当密化到一定程度时,其替代的直线轮廓就能满足形状上的要求。由于宏程序可以定义变量并赋值,也可进行运算及条件判断,构成循环转移,这样就可对那些能用数学函数关系表达的曲线进行连续的“拟合”处理,从而实现编程加工。

2.存在的关键难题

如图1所示工件的中间部分轮廓由椭圆的一部分组成，其中加工此零件选择毛坯为φ50mm的45钢，机床为配有FANUC0i系统的CK-6141型数控车床。因为零件轮廓较复杂，所以为了便于对椭圆曲线进行分析，这里将椭圆曲线单独从零件图中列出，并将椭圆中心设置为编程坐标原点。根据数控机床坐标系方向的确定原则，我们确定与主轴平行的轴为z轴；另一方向垂直于Z轴并平行与横向滑板移动方向为X轴，最终可得出椭圆的数学方程为：X2/576+Z2/1600=1。

通过仔细观察曲线方程，发现得到曲线数学方程的坐标系原点与编程加工时的坐标系原点存在不统一。出现的关键难题如下：

（1）两种情况下坐标系原点位置不一致。编程加工时我们原点通常确定在工件的右端面中心,即图1中的XOZ坐标系；在确定曲线方程时我们是以椭圆对称中心位置为坐标原点确定的，即图中X’O’Z’坐标系。

（2）两种情况下X坐标取值不一致。数控车编程中，平时为了便于测量，程序编制过程中X坐标通常取直径值，即直径编程；而在数学方程里面取得是半径值，即数学里面的坐标。

三、宏程序编程的教学思路

1.数学方程中的宏程序编制

先把非圆曲线从零件图中孤立出来进行分析，先在坐标系X’O’Z里面进行编程。

（1）确定自变量：一般情况下，非圆曲线中的X和Z坐标的其中一个都可以定义为自变量，但是一般情况下，我们选取变化范围较大作为自变量，并且要考虑函数表达式在宏程序中书写的方便。按照此原则，如图1所示，我们取Z轴方向作为自变量。

（2）根据零件图中曲线的加工确定自变量的变化范围：正常加工时我们都是从右向左进行加工,因此自变量z(即#1)的变化区间应为[0≤z≤40],从变化区间中就能知道自变量z(即#1)的取值变化是从z=40向z=0变化,因此在这里我们可以确定自变量z(即#1)的初值应赋为40(宏程序书写格式为#1=40)，条件判定循环语句为自变量z≥0（宏程序书写格式为#1GE0）。

（3）将数学方程进行转化：将方程转化为以Z为自变量，X为因变量的数学表达式，从而得到X的坐标，并且用FANUC系统的表达方式进行表达；即（若X取#2）#2=24*SQRT[1-#1*#1/1600].

（4）根据加工经验合理确定自变量z的步距:通过宏程序中的变量赋值的自增或自减,能够实现自变量按要求的变化趋势构成新的坐标值,而步距值的大小则最终决定了拟合线段的数量,步距值取得越小,则拟合线段数量越多,得到的曲线轨迹就越能接近于理想曲线,获得的表面精度越高,但运算量以及数据存储量也越大,这就要求数控系统具备较强的数据存储和处理能力,如低端的数控系统，由于处理速度慢，会导致不正常的处理而影响加工,所以步距值应根据零件的形状精度要求以及数控机床的配置情况进行合理选择，一般取值在0.2～0.5范围进行选取，宏程序书写格式为# 1=#1-0.5。

（5）利用条件判定循环语句让程序按指定的方向循环,即形成自变量不断按规律变化,通过函数方程表达式得出出新的因变量,从而获得利用G01加工所需要的终点坐标,从而实现非圆曲线椭圆的加工，条件判定语句的格式为IF[#1GE0]GOTO20。

（6）利用G01指令实现步距的移动，其终点坐标X和Z应为编程坐标系中的坐标值，而通过曲线函数表达式得到的坐标是以椭圆中心为原点获得的坐标,要通过表达式将其转化成编程坐标,这样刀具才能走出正确的路线实现加工。

按照以上思路，所编制出宏程序如下：O0001；M44；T0101；S800 M03；…；#1=40；N10#2=24*SQRT[1-#1*#1/1600]；G01 X[2*# 2]Z#1；#1=#1-0.5；IF[#1GE0]GOTO 10；…；M30。

2.进行坐标点的转换：选取某一具体坐标点进行分析转换

上面所编制的宏程序只是在坐标系X’O’Z里面进行的，而我们在实际编程加工时是在坐标系XOZ坐标系进行，那么如何进行坐标变换，才能得到我们的实际加工程序呢？下面我们可以通过在椭圆上选取任意某一具体的坐标点来进行分析，如我们选取图1中A点，由图中可知，A点在坐标系X’O’Z’里面的坐标是X为AH长度，Z为AI长度，而A点在坐标系XOZ里面的坐标为：X为AK长度，Z为负的AE，那么他们之间存在什么关系呢？仔细看图，会发现AK=42-AH，AE=（97-53.18）-AI，但是由于AE为负值，所以AE=AI-43.82，那么用变量表达为#3=42-#2，#4=#1-43.82，同样由于X方向为直径量，因此#3=2*[42-#2].所以，最终的加工程序为：O0002；M44；T0101；S800 M03；…；#1=40；N10#2=24*SQRT[1-#1*#1/1600]；#3=2*[42-#2]；#4=#1-42；G01 X#3 Z#4；#1=#1-0.5；IF[#1GE0]GOTO 10；…；M30。

四、结束语

根据以上教学思路分析，宏程序编程教学必须要抓住以下几点关键要素：

（1）宏程序编写的基础是建立在能够理解数控函数方程的基础上,对于曲线函数变量之间的关系一定要清楚,并最终学会确定自变量并得出正确的因变量表达式。

（2）根据零件图，找出非圆曲线自变量的取值范围，这一步很重要，由于我们在给自变量赋初始值时和条件判定跳转时都需要用到此取值范围。

（3）数控车里面宏程序编程时要考虑的关键是需不需要进行坐标系变换,平时编程原点基本设在零件右端面中心处,而一般我们第一步编制宏程序是在数学函数标准方程下的坐标系系里面进行的。

（4）对于自变量的步距值要选择恰当,粗加工零件时可取较大值;在精加工零件时为了确保零件的精度和表面质量应取较小值。

（5）上文所述的非圆曲线精加工宏程序,可在固定循环指令G73中应用加工。

（6）经多年实践经验证明,笔者所介绍的宏程序编写方法及编程思路可适用于大部分的非圆曲线编程。

[1]赵太平.数控车削编程与加工技术[M].北京理工大学出版社,2006.

[2]谢晓红.数控车削编程与加工技术[M].电子工业出版社, 2005.

[3]沈春根,等.数控车宏程序编程实例精讲[M].机械工业出版社出版，2012.