农用运输车用液力缓速器量纲分析与试验研究

赖建生，孔凡静

（1.广东科学技术职业学院，广东 珠海　519090；2.珠海市理工职业技术学校，广东 珠海　519090）

农用运输车用液力缓速器量纲分析与试验研究

赖建生1，孔凡静2

（1.广东科学技术职业学院，广东 珠海519090；2.珠海市理工职业技术学校，广东 珠海519090）

为研究农用运输车用液力缓速器的制动机理，基于π定理对影响液力缓速器制动性能的相关参数进行了量纲分析，得到了液力缓速器制动力矩与雷诺准则数、贝克莱准则数和欧拉准则数的关系式。以农用运输车液力缓速器样机THN15为例，综合运用台架试验和CFD计算，研究了不同充液率下雷诺准则数、贝克莱准则数和欧拉准则数对制动力矩的影响规律。结果显示：制动力矩都是随着欧拉准则数的增大而减小，随着雷诺准则数和贝克莱准则数的增大而增大；38%充液率时，雷诺准则数和贝克莱准则数随转速增大而减小，欧拉准则数则随转速增大而增大；95%充液率时，雷诺准则数和贝克莱准则数随转速增大而增大，欧拉准则数则随转速增大而减小。研究结果对完善农用运输车液力缓速器的设计及产品开发有较好的参考价值。

农用运输车；液力缓速器；量纲分析；制动力矩；充液率

农用运输车具有离地间隙较高、速度相对较低的特点，较适合县乡级条件道路的行驶，在农村具有较大的优势，是目前农村主要的货物运输工具之一。由于农用运输车常超载行驶在以丘陵山地坡陡弯多地形为主的农村道路，因此必须具备足够的持续制动能力以确保行车时的制动安全。但仅使用主制动器持续制动，主制动器热衰退严重，影响行车安全。因此，研究农用运输车用非接触式辅助制动装置具有重要的现实意义。液力缓速器具有制动力矩大、冲击均缓、没有热衰退、体积相对较小的优点，适合作为农用运输车辅助制动装置。但由于农用运输车价格低廉，目前有关农用运输车液力缓速器的研究较少，对其制动机理的研究文献暂未有检索结果。

前人对商用车液力缓速器进行了大量的研究，在几何结构参数的设计与优化、内流场特性、制动性能、温度场及散热性能等方面取得了较好的研究成果，为深入探索制动机理提供了借鉴。针对液力缓速器复杂的机构和较多的影响参数，文章在前人研究商用车液力缓速器的基础上，以与某公司在商用车液力缓速器研究基础上开发的农用运输车液力缓速器样机THN15为例，利用量纲分析的π定理，基于包含长度、质量、时间和温度四个基本量纲的介质比热容、密度、流速和液力缓速器循环圆湿周直径，依量纲齐次原理推导基于制动力矩、动力粘度、热导率、工作腔压力的无量纲相似准则数，建立相似准则数与制动力矩间的关系，结合台架试验和CFD计算，对不同充液率下相似准则数与转速关系、相似准则数与制动力矩关系进行分析研究，找出内在联系，为揭示农用车用液力缓速器制动机理，开发农用车用液力缓速器产品提供参考。

1　量纲分析

为研究介质粘度、密度等物性变化规律与影响，运用量纲分析法的π定理，以包含四个基本量纲的介质比热容、密度、流速和循环圆湿周直径为基本物理参数，依量纲齐次原理推导基于制动力矩、动力粘度、热导率、工作腔压力量纲的无量纲相似准则数，具体如下：

将液力缓速器的制动力矩Te，湿周直径l，工作腔压力p，介质密度ρ、动力粘度μ、热导率λ、定压比热容Cp、流速u的量纲矩阵列出如表1所示。

表1　液力缓速器制动性能相关物理参数量纲表

表1中L、M、T、θ是长度、质量、时间和温度的量纲，是流体力学的基本量纲。用涉及r个基本物理量的n个有量纲物理量来描述某一物理现象时，可以转变为用n-r个无量纲量来描述同一物理现象。这些无量纲的数称为π项，这就是量纲分析中的π定理，也称为Buckingham定理。

根据π定理，将表1中包含长度、质量、时间和温度四个基本量纲的ρ、Cp、u、l独立物理参数作为基本物理参数，把制动力矩Te、动力粘度μ、热导率λ、工作腔压力p无量纲化。以Te为例，有

a、b、c、d为ρ、Cp、u、l四个物理参数的量纲指数，由表1有

由量纲齐次原理有

解（3）得a=1，b=2，c=3，d=0，由此可得πTe

同理可得πμ、πλ、πp如下

式（5）中Re、Pr、Pe、Eu分别为雷诺准则数、普朗特数、贝克莱准则数和欧拉准则数。由式（4）有

由式（6）可知制动力矩和密度、流速平方、循环圆湿周直径三次方是成正比的，雷诺准则数、贝克莱准则数和欧拉准则数和制动力矩之间有着密切的联系。

2　试验研究

2.1试验设备

设备包括CFD计算设备（软件：ANSYS14.5，硬件：CPU为8核4GHz主频、内存16G、显存2G独立显卡的组装计算机）、台架试验设备（试验台架、试验控制柜、试验软件及其他附件）和试验样机（THN15）。

试验台架含三相异步电动机、联轴器、转矩转速测量仪、冷却系统等，如图1所示，试验控制柜、试验软件及其他附件如图2所示，台架试验设备的关键组件及参数如表2所示。

图1　试验台架

图2　台架试验控制柜

表2　台架试验设备的关键组件参数

THN15是某公司研发的农用运输车用并联中置式液力缓速器（安装在传动轴中间），额定制动力矩1500N·m，总体设计尺寸为310mm×435mm×490mm，如图3所示，具体参数如表 3所示。

图3　THN15农用车用液力缓速器样机

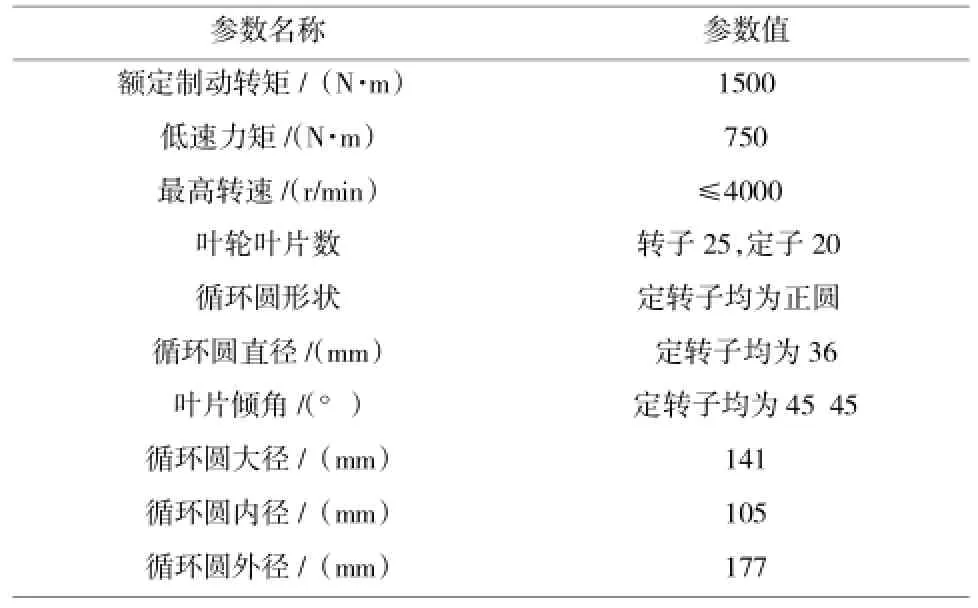
表3　THN15技术参数

2.2试验材料

试验用油液介质采用Helix ultra SM 5W-40全合成润滑油，具体参数如表4所示。空气介质为干空气，不同温度下具体参数如表5所示。

表45　W-40润滑油参数

表5　不同温度下干空气参数

5W-40全合成润滑油的粘温特性符合瓦尔塞方程，如式（7），密度和温度的关系用式（8）确定。

式（7）中ν为运动粘度，单位mm2/s，T为热力学温度，单位为K，a、b、c为系数，其中a取0.6，b和c通过油液介质给定的温度和对应的粘度值求出。根据表4数据，算出b= 2.7793，c=7.2113。式（8）中ρt为t℃对应的油液介质密度，ρ0表示在15℃对应的油液介质密度值，即ρ0=851kg·m-3，t为油液介质的温度，单位℃。

2.3充液率与混合介质密度的确定

针对液力缓速器部分充液的气液两相流场特性，参考前人用PIV法流场测试结果假定气液两相是分层均匀的，定义充液率为油液介质的体积占工作腔体积的百分数，如式（9）所示：

式（9）中Ff为充液率，单位%，Voil为油液介质的体积，单位mm3，Vair为空气介质的体积，单位mm3，Voil+Vair等于液力缓速器工作腔的容积。由此，可以确定工作腔混合介质的密度ρmix：

式（10）中ρair为空气介质在对应温度下的密度，单位kg·m-3，由表5确定，ρoil为油液介质在对应温度下的密度，单位kg·m-3，由式（8）确定，Ff为充液率，单位%，由式（9）定义。

2.4充液率与制动气压关系的确定

液力缓速器充液率在目前条件下较难准确测量，文章通过CFD计算与台架试验确定充液率与制动气压之间的关系。CFD计算以定转子工作腔为研究对象，抽取全流道计算流域并设置为气液两相介质模型，用SST-kω双方程湍流模型和Heat Transfer Total Energy热量传输求解模型进行数值求解。在80%充液率及以上时，空气介质设为直径2mm的离散态，80%充液率以下时空气介质设为连续形态。定转子交界面设置为流体——流体交界面，耦合方式为GGI。SST-kω双方程湍流模型的相关参数设置如下：σk1=0.85，σω1=0.5，β1=0.075，γ1=0.553，σk2=1.0，σω2=0.856，β2=0.0828，γ2=0.440，β*=0.09，k=0.41，α1=0.31。设定转速600r/min，介质温度60℃不变，充液率从100%到10%变化，先每隔10%进行计算。油液介质粘度、密度根据表4和式（7）、（8）进行设置，定压比热容和热导率因受温度变化较小，假定不变，按表4的值进行设置。空气介质参数参考表5进行设置。液力缓速器特征长度l取其循环圆湿周直径，即l=0.018m，故湍流的强度尺度L=0.7*l=0.00126m，代入下式可求出湍粘度μt。

式中μt为湍粘度，k为湍动能，取值0.41，ω为比耗散率，Cmu为湍流模型计算系数，取0.09，ρmix为工作腔混合介质的密度 ρmix，由式（10）确定。

将以上的相关参数代入进行CFD计算，残差设定当所有变量的残差值都小于10-3（即监控纵坐标中的1.0e-03）且增加的求解目标制动转矩监测值无限趋于某一值时就认为计算收敛。计算完成后运用CFD-Post提取制动制动转矩等数据。

台架试验在相同转速和介质温度下从Ⅰ档2.8bar到Ⅶ档0.66bar进行制动转矩试验，记录每一档位的制动转矩值，并与CFD计算的制动转矩值进行比较。比较后根据台架试验的值再次调整充液率进行CFD计算，直至两者误差小于5%。两者结果如表6所示。

表6　台架试验与CFD计算制动转矩值对比

从表6可以看出台架试验的制动转矩值都稍大于CFD计算的制动转矩值，两者最大误差为4.3%，出现在2.8bar制动气压对应的95%充液率下，两者最小误差0.12%，出现在1.8bar制动气压对应的72%充液率下。为了更直观对比制动气压与充液率的关系，将两者如图4如下。

图4　制动气压与充液率关系

从图4可以看出充液率与制动气压是呈显著线性正相关关系（p＜0.04），因此，可用制动气压值表示充液率。为了再次验证两者关系的正确，取2.8bar对应的95%充液率与0.66bar对应的38%充液率分别进行相同温度下的制动转矩随转速变化台架试验与CFD计算，结果显示，在相同温度下台架试验与CFD计算制动转矩随转速变化的趋势是基本一致的，2.8bar对应95%充液率时两者最大误差为3.6%，0.66bar对应38%充液率时两者最大误差为3.34%。这表明图4的制动气压与充液关系式是可信和可靠的。

2.5试验过程

在台架上，分别在制动气压0.66bar、介质温度稳定在70℃，制动气压1.0bar、介质温度稳定在75℃，制动气压1.5bar、介质温度稳定在80℃，制动气压1.8bar、介质温度稳定在85℃制动气压2.0bar、介质温度稳定在90℃，制动气压2.8bar制动气压和介质温度稳定在95℃工况下进行制动转矩与转速的特性试验。CFD则分别在对应的充液率下进行仿真计算，计算后用CFD-Post提取制动制动转矩等数据。

3　试验结果与分析

3.1不同充液率下的制动特性结果

限于篇幅，文章仅选择95%充液率（对应2.8bar）和38%充液率（对应0.66bar）的结果进行分析。两者制动力矩与转速关系的台架试验结果与CFD计算结果如图5所示。

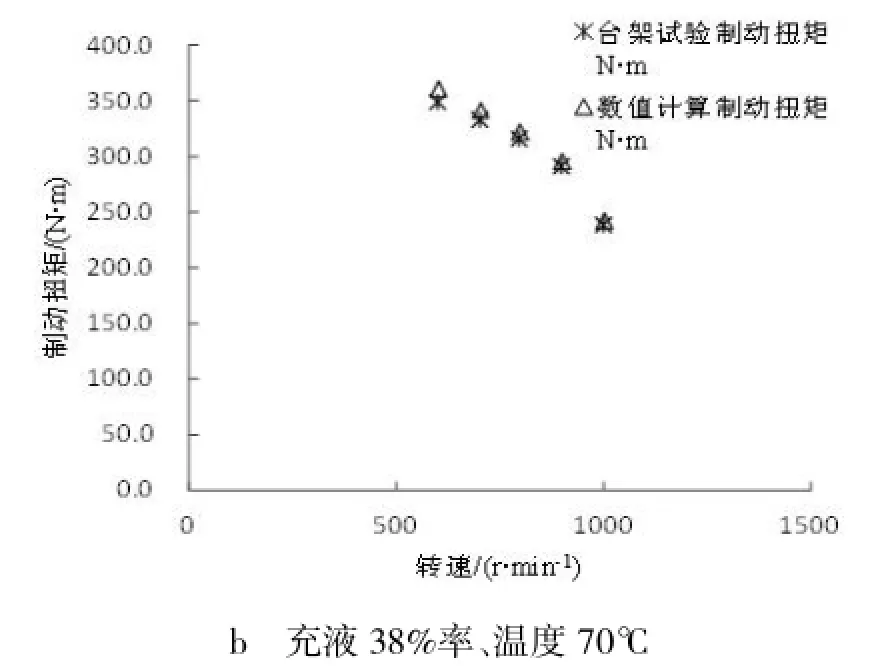
图5　台架试验和数值计算制动力矩——转速特性对比图

从图 5可以看出台架试验和CFD计算的制动力矩结果变化趋势基本一致：介质温度都是95℃时，2.8bar台架试验制动力矩与95%充液率时CFD计算制动力矩都随转速升高增大，两者最大绝对误差为3.6%；介质温度都是70℃时，0.66bar台架试验制动力矩与38%充液率时CFD计算制动力矩都随转速升高减小，两者最大误差为3.34%。误差在合理范围内，CFD计算结果是可信的。

为此，可利用CFD计算气液两相混合介质表观动力粘度、流速、密度、压力、热导率和比热容，结果如表7和表8所示。

表7　液力缓速器工作介质物性参数（95%充液率、温度95℃）

表8　液力缓速器工作介质物性参数（38%充液率、温度70℃）

3.295%充液率、温度95℃下的相似准则数

利用公式（5）和表7的数据计算雷诺准则数、贝克莱数和欧拉数，结果如表9所示。

表9　液力缓速器相似准则数计算结果（95%充液率、温度95℃）

从表9可以看出，在95%充液率、温度95℃时，雷诺准则数、贝克莱准则数都是随转速升高增大，460r/min时最小，分别为12778和9941578；900r/min时最大，分别为137776和21765380；欧拉准则数则随转速升高减小，900r/min时最小为1.095，460r/min时最大为1.347。以制动力矩为横坐标，准则数为纵坐标，如图6、图7所示。

图6　雷诺准则数、贝克莱准则数与制动力矩关系（95%充液率、温度95℃）

图7　欧拉准则数与制动力矩关系（95%充液率、温度95℃）

将雷诺准则数与制动转矩进行曲线拟合，拟合结果表明幂指数关系具有较好的拟合优度，拟合方程和判定系数如所示（P＜0.01）；贝克莱准则数与制动转矩曲线拟合结果表明线性关系具有较好的拟合优度，拟合方程和判定系数如所示（P＜0.01），具体拟合方程和判定系数如图6所示。从中可以看出雷诺准则数和贝克莱准则数都随制动力矩增大而增大。

从图7可已看出欧拉准则数随制动力矩增大而减小。这说明几何结构确定的液力缓速器，在95%充液、介质温度95℃时，随着转速的提高，介质的粘度变小，流速变大，由式（6）可知制动力矩增大，由式（5）可知雷诺准则数和贝克莱准则数也增大，而欧拉准则数则减小。

3.338%充液率、温度70℃下的相似准数

利用式（5）和表8的数据计算雷诺准则数、贝克莱数和欧拉数，结果如表10所示。

表10　液力缓速器相似准则数计算结果（38%充液率、温度70℃）

从表10可以看出，在38%充液率、温度70℃时，雷诺准则数、贝克莱准则数都是随着转速的升高而减小的，1000r/min时最小，分别为7914和7188550。600r/min时最大，分别为22199和12765149；欧拉准则数则随转速的升高而增大，100r/min时最大为1.388，460r/min时最小为1.369。以制动力矩为横坐标，准则数为纵坐标，如图8、图9所示。

图8　雷诺准则数、贝克莱准则数与制动力矩关系（38%充液率、温度70℃）

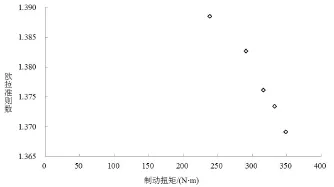
图9　欧拉准则数与制动力矩关系（38%充液率、温度70℃）

从图8可以看出雷诺准则数和贝克莱准则数都是随制动力矩增大而增大，将其进行曲线回归拟合，拟合结果表明二次多项式函数关系具有较好的拟合优度，其中贝克莱准则数与制动力矩关系拟合方程的判定系数P＜0.0005，雷诺准则数与制动力矩关系拟合方程的判定系数P＜0.005。在制动力矩小于300N·m时，雷诺准则数和贝克莱准则数随制动力矩增加变化平缓，大于300N·m后变化速率迅速增大。具体拟合方程和判定系数如图8所示。

从图9可以看出欧拉准则数和制动力矩也是呈递减关系的。这说明几何结构确定的液力缓速器在38%充液、介质温度70℃时，随着转速提高，介质的粘度变大，流速减小，由式（6）可知制动力矩减小，由式（5）可知雷诺准则数和贝克莱准则数也减小，而欧拉准则数则增大。初步介质的流变特性呈现出剪切变稠的特性。

4　结语

（1）液力缓速器雷诺准则数、贝克莱准则数越大制动力矩越大，欧拉准则数越小制动力矩越大，表明以液力缓速器循环圆湿周直径，介质密度、流速、定压比热容为基本物理参数，基于表观动力粘度、热导率、工作腔压力和制动力矩的量纲推出的制动力矩与密度、流速、特征长度、雷诺准则数、贝克莱准则数、和欧拉准则数的关系式是正确的，可用以阐述液力缓速器的制动机理。

（2）液力缓速器雷诺准则数、贝克莱准则数和充液率有关，95%充液率，介质温度稳定在95℃时，这两个准则数是随着转速的升高而增大；但在38%充液率，介质温度稳定在70℃时，这两个准则数是随着转速的升高而减小。

（3）液力缓速器欧拉准则数也和充液率有关，95%充液率，介质温度稳定在95℃时，随着转速的升高而减小；但在38%充液率，介质温度稳定在70℃时，是随着转速的升高而增大。

［1］中华人民共和国质量监督检验检疫总局.机动车运行安全技术条件［S］.北京：中华人民共和国国家标准化管理委员会，公安部道路交通管理标准化技术委员会，2012.

［2］何仁.汽车辅助制动装置［M］.北京：化学工业出版社，2005.

［3］黄俊刚，李长友，文光安.液力缓速器全流道式制动流场数值计算方法研究［J］.机床与液压，2016，（4）：78-82.

［4］黄俊刚，张胜宾，张晶晶.叶片倾角因素对液力缓速器制动力矩及其容积比的影响分析［J］.广东交通职业技术学院学报，2016，（1）：39-44.

［5］闫清东，穆洪斌，魏巍，等.双循环圆液力缓速器叶形参数优化设计［J］.兵工学报.2015，36（3）：385-390.

［6］吕金贺，褚亚旭.叶片楔角对液力缓速器内流场的影响分析［J］.北华大学学报（自然科学版），2013，（5）：613-616.

［7］Bo Z，Wei W，Qing-Dong A Y.Research on Parametric Design of Hydraulic Retarder Cascade［J］.Software Engineering and Knowledge Engineering，2012，2（115）：535-541.

［8］饶银，李长友，黄俊刚.液力缓速器双向流固耦合研究［J］.机床与液压，2015，（1）：116-122.

［9］Li R，Yang J，Zhang W.Simulation Study of the Vehicle Hydraulic Retarder［J］.International Journal of Control and Automation，2015，8 （2）：263-280.

［10］余国保，周云波.基于大涡模拟法的液力缓速器内流场仿真分析［J］.机械工程与自动化，2014，（1）：52-54.

［11］罗天洪，贺海燕.液力计算法及DFI-PID下液力缓速器恒力矩制动性能建模与仿真分析［J］.机械科学与技术，2015，（8）：1283-1288.

［12］李淑梅，罗卫东，柳慧谱.加装液力缓速器商用车的制动稳定性控制研究［J］.机械设计与制造，2014，（8）：137-139.

［13］孙博，李环.整车散热系统对液力缓速器持续制动性能的影响［J］.公路与汽运，2014，（3）：24-25.

［14］袁哲，马文星，卢秀泉，等.液力减速器动态制动性能预测分析［J］.吉林大学学报（工学版），2013，（S1）：160-164.

［15］林彩霞，赵旭飞.液力缓速器能量耗散方程的建立［J］.机械设计，2014，（3）：80-84.

［16］哲袁，马文星，李华龙.重型车液力减速器的换热器匹配与仿真分析［J］.吉林大学学报（工学版），2013，43（增刊）：526-529.

［17］袁哲.重型车液力缓速器热流耦合与散热系统研究［D］.长春：吉林大学，2013.

［18］李晓文，李长友，李真太，等.液力缓速器热交换管路能头损失的数值计算［J］.机床与液压，2012，40（7）：26-28.

［19］姬书得，张利国，刘雪松，等.基于相似理论解决水轮机转轮数值分析困难的方法［J］.机械工程学报，2010，46（8）：83-87.

［20］李长友.工程热力学与传热学［M］.北京：中国农业大学出版社，2014.

［21］张云峰，罗嵩容，罗稀玉，等.重力热管内水相变换热的数值模拟［J］.长沙理工大学学报（自然科学版），2016，（1）：69-74.

［22］Lloyd T P，James M.Large eddy simulations of a circular cylinder at Reynolds numbers surrounding the drag crisis［J］.Applied Ocean Research，2015，（1）：1-11.

［23］Wanga Y，Shua C，Yangb L M.An improved multiphase lattice Boltzmann ux solver for three-dimensional ows with large density ratio and high Reynolds number［J］.Journal of Computational Physics，2015，（302）：41-58.

［24］Yamamoto Y，Kunugib T.Modeling of MHD turbulent heat transfer in channel flows imposed wall-normal magnetic fields under the various Prandtl number fluids［J］.Fusion Engineering and Design，2016，4（1）：1-7.

［25］Salehipour H，Peltier W R，Mashayek A.Turbulent diapycnal mixing in stratified shear flows：the influence of Prandtl number on mixing efficiency and transition at high Reynolds number［J］.Journal of Fluid Mechanics，2015，773：178-223.

［26］Ansys Inc.Ansys CFX-solver theory guide［M］.Canonsburg：Ansys Inc，2015.

［27］李兴虎，赵晓静.润滑油粘度的影响因素分析［J］.润滑油，2009，24（6）：64.

［28］刘传安，周珺.机油粘度与温度关系的研究［J］.拖拉机与农用运输车，2005，（6）：61-63.

［29］李雪松，程秀生，苗丽颖.液力缓速器部分充液流场大涡模拟及特性预测［J］.中南大学学报（自然科学版），2012，43（5）：1717-1723.

［30］闫清东，邹波，魏巍，等.液力减速器充液过程瞬态特性三维数值模拟［J］.农业机械学报，2012，43（1）：12-17.

［31］Dc W.Turbulence modeling for CFD［M］.3rd Edition ed.Washington DC：DCW Industries Inc.，2006.

［32］任芸，刘厚林，舒敏骅，等.考虑旋转和曲率影响的SST k_w湍流模型改进［J］.农业机械学报，2012，43（11）：123-128.

Analysis and Experimental Research on Farm Transport Vehicle Hydraulic Retarder Caliber Steel

LAI Jian-sheng1，KONG Fan-jing2
（1.Guangdong Vocational College of Science and Technology，Zhuhai，Gungdong 519090，China；2.Nai Jiansheng Zhuhai Technology Vocational College，Zhuhai，Guangdong 519090，China）

In order to research farm transport vehicle hydraulic retarder braking mechanism，based on the analysis of theorem of PI to the related parameters affecting the braking performance of the hydraulic retarder on the dimensional，this paper concludes the relation quota between the braking torque and hydraulic retarder rule of Reynolds number，Berkeley code number and the rule of euler number.Taking farm transporter prototype THN15 hydraulic retarder as an example，this paper applies use of bench test and CFD calculation，studies the rule of Reynolds number under different charging rates，Berkeley criteria and euler rule of the influence law of braking torque.The result shows the braking torque decreases as the rule of euler number increases，as the rule of Reynolds number and Berkeley code number increases；38%liquid rate，the rule of Reynolds number and Berkeley code number decreases with increasing speed，rule of euler number increases with the increase of rotational speed and；95%liquid rate，Renault，criterion and rule of Berkeley with speed increases，the rule of euler number decreases with increasing rotating speed.The research results has good reference value to improve the farm transporter of hydraulic retarder design and product development.

farm transporter；hydraulic retarder；dimensional analysis；braking torque；charging rate

U463.53

A

2095-980X（2016）07-0048-06

2016-06-18

赖建生（1981-），男，广东河源人，讲师，主要研究方向：汽车技术教学与研究。