马尔科夫链在药物动力学建模中的应用
刘爱红,杨 光
(沈阳师范大学 数学与系统科学学院,沈阳 110034)
基础科学和工程
马尔科夫链在药物动力学建模中的应用
刘爱红,杨光
(沈阳师范大学 数学与系统科学学院,沈阳 110034)
摘要:研究马尔科夫链在药物动力学建模中的应用问题。首先给出单室静脉注射和血管外给药两种模型下的转移概率矩阵,根据吸收马尔科夫链的基本性质推算转移概率矩阵的t次幂,给出t时刻吸收部位和体内药量的表达式;然后将马尔科夫链与非线性回归结合起来,运用复合函数模型拟合数据,估计药物动力学模型参数;最后利用残差分析法对随机抽取的一组数据计算得出,利用马尔科夫链建立的模型比传统的药物动力学微分方程模型与实际数据拟合的程度高,从而给出一种新的药物动力学建模方法。
关键词:马尔科夫链;静脉注射;血管外给药;单室模型;转移概率矩阵;非线性回归
药物动力学是将数学与医学结合起来的一门交叉学科,模型建立与参数估计一直是其研究的两个主要内容,国内外已有大量相关文献及研究成果。大部分文献都将药物的吸收和消除速率常数作为系数建立微分方程模型[1],虽能直观地反映药量的动态变化,但根据模型计算出的体内药量和吸收部位药量与实际药量误差较大。在药动学参数估计方面,大部分文献都在微分方程模型下运用残数、Wagner-Nelson等方法[1],同样误差较大的问题很难回避。到目前为止,马尔科夫链被广泛应用于人口预测、环境预测等问题[2-8],但甚少有文献将马尔科夫链应用于药动学的建模中,亦鲜有考虑将其与非线性回归结合起来估计参数的问题,本文将在这两方面进行大胆的尝试,旨在提高模型的精确性。
本文考虑药物在体内的变化符合时齐的马尔科夫链这一事实,在单室模型下,首先,给出静脉注射、血管外给药两种方式下的转移概率矩阵,利用吸收马尔科夫链的性质推算出转移概率矩阵的t次幂,进而给出t时刻的体内、吸收部位药量表达式;然后,对测得的药量数据进行非线性回归分析,根据估计出的参数给出吸收、消除速率常数计算公式;最后,对随机抽取的一组数据,借助残差平方和对本文运用马尔科夫链建立的模型与传统的药动学微分方程模型进行比较,并得出本文建立的模型更精确的结论。
1 马尔科夫链确定t时刻体内药量
药物在体内的变化符合时齐的马尔科夫链[9],n室模型对应的转移概率矩阵文献[10]已经给出,下面推算单室模型的转移概率矩阵的t次幂。
定理1在单室模型下,t步转移概率矩阵为:
(1)对于静脉注射给药方式:
(1)
(2)对于血管外给药方式:
(2)
证明:(1)对于静脉注射单室模型,其转移概率矩阵为:
经计算有:
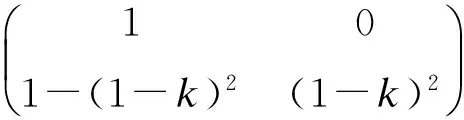
……
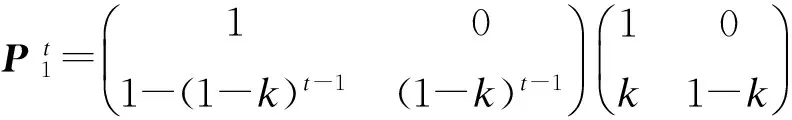
(2)对于血管外给药方式,其转移概率矩阵如下:
下面,利用吸收马尔科夫链的性质,推算出t时刻时体内药量、吸收部位药量的表达式。
定理2在单室模型下,生物利用度为F,给药x0后,t(t∈N)时刻药量表达式为:
(1)对于静脉注射给药方式:
x(t)=Fx0(1-k)t
(3)
(2)对于血管外给药方式:
xa(t)=Fx0(1-ka)t
(4)
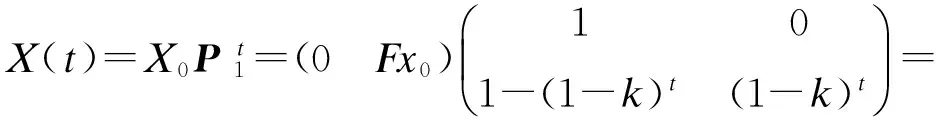
(Fx0-Fx0(1-k)tFx0(1-k)t),因此,t时刻时的体内药量为Fx0(1-k)t。
(2)血管外给药模型下,初始向量为:X0=(0Fx00),同上可证。
2 非线性回归估计药动学模型参数
根据给药后测得的体内药量或血药浓度数据可知:无论采用静脉注射还是血管外给药方式,体内药量的变化均不是线性的,因此需结合软件运用非线性回归[11-15]估计药动学参数。
对于静脉注射模型,(3)式显然满足复合函数模型:
(5)
因此,对测得的体内药量数据进行非线性回归分析,运用复合函数模型进行拟合,得出b0、b1的估计值。b1应为1-k的估计值,即得出模型参数k的估计式如下:
k=1-b1
(6)
对于血管外给药模型,由于对大部分药物来说,ka>k,当t充分大时,(1-ka)t趋近于0,且药物只有消除过程,因此,式(4)中二式化为:
(7)
显然,式(7)亦符合模型式(5)。同理可得参数k、ka的估计式为:
(8)
3 模型的比较
对于随机抽取的一组数据,下面利用残差平方和分析法来对本文建立的模型和传统的药动学微分方程模型与该组数据的拟合程度进行比较,进而比较两模型的精确度。
(1)对于静脉注射给药方式,当x0=1 050 mg,F=1时,测得的药量数据如表1所示[1]:

表1 静脉注射给药下的体内药量数据表
1)利用马尔科夫链建立药动学模型,则根据(3)式可给出体内药量表达式:
x(t)=1 050(1-k)t
(9)
对表1中的数据进行非线性回归分析,选择复合函数模型拟合,可得:b0=1 050.191,b1=0.732,带入(6)式可知k的估计值为0.268 h-1。将k的值带入(9)式有:
x(t)=1 050×0.732t
(10)
2)建立传统的药动学微分方程模型,运用残数法估计出的消除速率常数k已于文献[3]第八章给出,即0.314 h-1,则体内药量表达式为:
x(t)=1 050×e-0.314 t
(11)
3)根据(10)、(11)式可分别计算出两模型下各个时刻体内药量的拟合数据,则两模型拟合药量与实际药量的残差平方和依次为0.1619、22.4121,显然,运用马尔科夫链所建立模型的拟合数据与实际数据的残差平方和更小,故在静脉注射给药方式下,对于表1中的数据,本文建立的模型比传统的药动学微分方程模型更精确。
(2)对血管外给药方式,当x0=500mg,F=1时,取药物只有消除过程时的数据如下[1]:

表2 血管外给药下的体内药量数据表
1)利用马尔科夫链建立药动学模型,则根据式(4)中二式可给出体内药量表达式如下:
(12)
对表2中的数据进行非线性回归分析可得:b0=645.636,b1=0.935,带入(8)式可知k的估计值为0.065 h-1,ka的估计值为0.288 h-1。故(12)可表示为:
(13)
2)建立传统的药动学微分方程模型,运用残数法估计出的k、ka的值亦已于文献[1]第八章给出,且依次为0.068 h-1、0.252 h-1,则体内药量表达式为:
(14)
3)两模型的残差平方和依次为4.2487、21.2208,同样可看出,利用马尔科夫链所建立模型的拟合数据与实际数据的残差平方和更小,所以在血管外给药方式下,对于表2中的数据,本文建立的模型比传统的药动学微分方程模型更精确。
4 结论
在单室模型下,本文运用马尔科夫链建立药物动力学模型,推算出t时刻体内和吸收部位药量的表达式,运用非线性回归分析方法估计所建立模型的参数(药物的吸收和消除速率常数),并分别在静脉注射、血管外给药两种方式下,对随机抽取的一组数据,借助残差平方和对本文所建立的药动学模型与传统的用药动学微分方程模型进行比较,得出本文运用马尔科夫链建立的药动学模型更精确,进而为药动学模型的建立提供一种新的方法。
参考文献(References):
[1]梁文权.生物药剂学与药物动力学[M].北京:人民卫生出版社,2007.
[2]徐克学.生物数学[M].北京:科学出版社,1999.
[3]苑旭东,张烁,井元伟.基于马尔科夫过程的单路由网络建模[J].沈阳大学学报(自然科学版),2012(4):45-48.
[4]孙鹏,张强,涂新军,等.基于马尔科夫链模型的鄱阳湖流域水文气象干旱研究[J].湖泊科学,2015(6):1177-1187.
[5]廖普明.基于马尔科夫链状态转移概率矩阵的商品市场状态预测[J].统计与决策,2015(1):97-100.
[6]谷秀娟,李超.基于马尔科夫链的房价预测研究[J].消费经济,2012(5):40-43.
[7]程晓苏.马尔科夫链在教学评价中的应用[J].科技信息,2014(11):112-113.
[8]张婧,向泽林.马尔科夫链在零售商品销售预测中的应用[J].成都航空职业技术学院学报,2013(3):54-56.
[9]宋占杰,王家生,王勇.随机过程基础[M].天津:天津大学出版社,2011.
[10]丁勇.用马尔科夫链估算药物在体内的平均转运时间[J].数理统计与管理,2009,28(4):751-755.
[11]孙艳玲,何源,李阳旭.例说SPSS统计分析[M].北京:人民邮电出版社,2010.
[12]武松,潘发明.SPSS统计分析大全[M].北京:清华大学出版社,2014.
[13]DOUGLAS M.BATES,DONALD G.WATTS.非线性回归分析及其应用[M].北京:中国统计出版社,1997.
[14]陈永胜.基于MATLAB和SPSS的非线性回归分析[J].牡丹江大学学报,2009(5):101-104.
[15]谢兰,高东红.非线性回归方法的应用与比较[J].数学的实践与认识,2009(10):117-122.
(责任编辑:吴萍英文审校:王云雁)
收稿日期:2015-11-15
基金项目:辽宁省科学技术厅自然基金(项目编号:2014020120);辽宁省教育厅科学研究一般项目(项目编号:L2013420)
作者简介:刘爱红(1990-),女,辽宁北票人,硕士研究生,主要研究方向:生物统计,E-mail:1278582891@qq.com;杨光(1964-),女,辽宁抚顺人,教授,博士,主要研究方向:生物统计,E-mail:yg19640202@aliyun.com。
文章编号:2095-1248(2016)02-0093-04
中图分类号:O211.62
文献标志码:A
doi:10.3969/j.issn.2095-1248.2016.02.017
Application of Markov chain in pharmacokinetics modeling
LIU Ai-hong,YANG Guang
(School of Mathematics and Systems Science,Shenyang Normal University,Shenyang 110034,China)
Abstract:The application of Markov chain in Pharmacokinetics modeling was researched.Firstly,transition probability matrixes under both one-compartment intravenous injection model and one-compartment extravascular administration model are presented respectively.The t-th power of the matrix was deduced based on basic natures of absorbed Markov chain,and expressions of dose in vivo and in absorption site are obtained;then,Markov chain and Nonlinear regression are linked to estimate parameters of pharmacokinetics with compound function model to simulate data;finally,residual sum of squares was employed from a set of data extracted randomly to show the result that the model built by Markov chain has a higher degree of fitting for actual data than the model established by traditional differential equation,and a new modeling method for Pharmacokinetics is proposed.
Key words:markov chain;intravenous injection;extravascular administration;one-compartment;transition probability matrix;nonlinear regression

