浅析化归思想在高中数学教学中的应用

许世林（重庆市南坪中学校）

浅析化归思想在高中数学教学中的应用

许世林
（重庆市南坪中学校）

化归思想指的是将未知转化为已知，将难化易，将各种难以理解的问题转化为已知的、熟悉的问题，以更好、更快地解决问题。在高中数学教学中，化归思想的应用更为广泛。结合实际，浅析化归思想在高中数学教学中的应用。

化归思想；高中数学；基本原则

波利亚曾经说过：“解决问题需要不断地变换，需要一再变化它，重新叙述它，直到最后成功地找到某些有用的东西为止……”这也提示我们在解决一些复杂问题时需要掌握和善于运用一种转化思想，即化归思想，也就是善于将复杂的问题往容易解决的、已知的、熟悉的问题方向转化。因数学具有的独特特点，将化归思想贯穿在整个问题解决和教学过程中十分重要且必要，为了更好地发挥化归思想在数学问题解决中的作用，促使学生更好地掌握和运用化归思想，下面笔者对化归思想在高中数学教学中的应用加以浅析。

一、在高中数学教学中应用化归思想的基本原则

1.熟悉化原则：把未知不熟悉的数学问题转化为已知熟悉的数学问题，借助已经掌握的数学知识和解决方法来解决未知不熟悉的数学问题。

2.简单化原则：有一些数学问题常常含有不少复杂繁琐的条件，使学生看到此类问题无从下手。此时，教师应当指导学生善于提取关键词，用简洁的方式表示该数学问题想要表示的含义，便于学生找到解决问题的突破口。

二、化归思想指导下经常采用的几种数学方法

1.直接转化法：将所需要解决的数学难题直接转化为涉及基本定义、定理、公式或基本图形的数学问题，以便于利用已经掌握的数学知识和技巧加以解决。

2.换元法：指的是把形式较复杂或者不标准的方程、不等式、函数化归为形式较简单易于解决的基本问题。

3.坐标法：这种方法也比较常见，即在掌握平面图形或者空间几何图形实际情况的基础上，画出平面的直角坐标系或空间的直角坐标系，采用坐标的形式表示平面图形或者空间几何图形的各个点，借助已经掌握的坐标计算法将所需要的数量关系表示出来。在数学问题的解决中，最常见的就是借助直角坐标系把几何问题转化为向量问题或者代数问题。值得注意的是，这种方法需要学生具有较强的运算能力。

4.类比法：指的是借助类比推理把未知的不熟悉的问题类比为已知的、已经解决的简单问题，化难为易。例如，等差数列类比、等比数列类比、三种圆锥曲线性质之间的类比等。

三、化归思想在高中数学教学中应用的基本类型

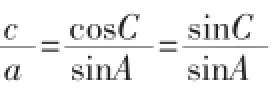
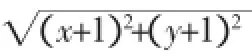
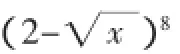
总之，在高中数学教学过程中，教师应当注重借助具体的数学问题使学生感受到化归思想在某些数学问题解决中的重要作用，指导学生掌握将化归思想应用于数学问题解决中的方法，以促使学生形成良好的数学思维、提高学生解决数学问题的能力。

靳世杰.高中数学化归思想教学之我见［J］.数学学习与研究，2014（9）：58.

·编辑 薄跃华

许世林，就职于重庆市南坪中学校，本科，研究方向为数学教育教学。