关于近似R-正交的注记

孔亮，王念良

（商洛学院 数学与计算机应用学院，陕西商洛　726000）

关于近似R-正交的注记

孔亮，王念良

（商洛学院 数学与计算机应用学院，陕西商洛726000）

在复赋范线性空间，利用范数导数的定义和性质，并运用算子论方法，证明了近似R-正交是近似ρ-正交，给出了弱近似R-正交的定义，并证明了在一定条件下，近似ρ-正交是弱近似R-正交。

R-正交；近似R-正交；弱近似R-正交；近似正交

在20世纪初，R-正交、B-正交、I-正交等正交性定义被相继引入用来研究赋范线性空间的几何性质［1-3］。此后，新的正交性定义被不断引入和研究，比如文献［4］在Banach空间中给出新的正交性定义，文献［5-6］引入了ρ-正交定义。近年来，许多学者推广了以上正交性定义得到相应的近似正交性定义。文献［7-8］在复赋范线性空间中给出了近似B-正交的定义和性质，文献［9-10］在实赋范线性空间中分别引入了近似I-正交和近似R-正交的定义，关于其它各种正交性和近似正交性定义和相关性质已有许多研究［11-16］。受上述定义和结论的启发，本文在复赋范线性空间，证明近似R-正交是近似ρ-正交，给出弱近似R-正交的定义，并证明在一定条件下，近似ρ-正交是弱近似R-正交。

1　预备知识和结论

X在本文中均表示复赋范线性空间，R表示实数集，C表示复数集，U（0；δ）表示在复平面上以原点为中心，以δ＞0为半径的邻域。

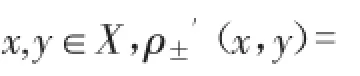
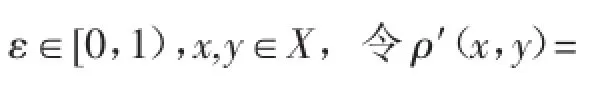
文献［16］在复赋范线性空间中给出了范数导数的性质。

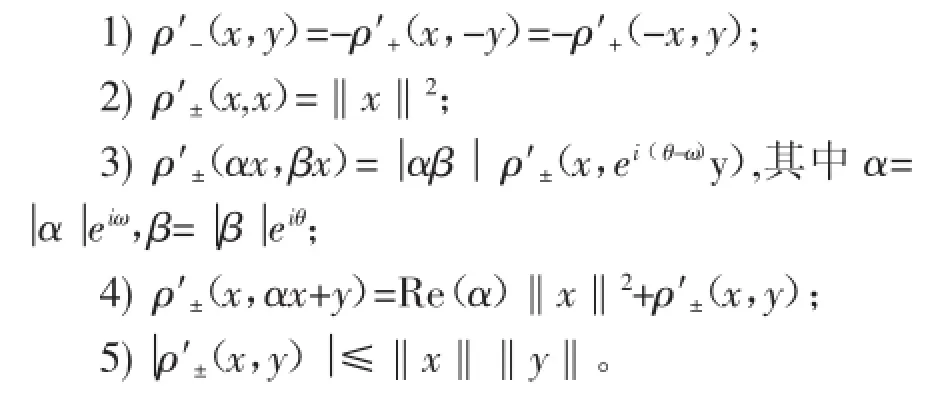
本文利用定义3和定理1，主要得到下面的结论。

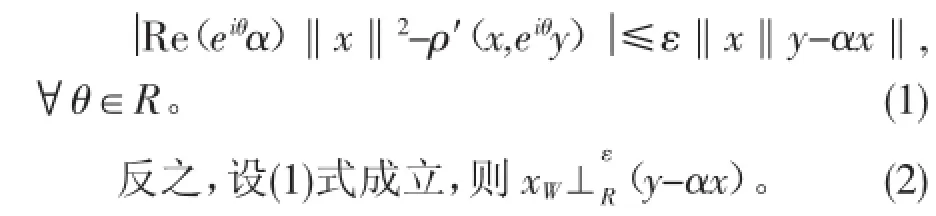
2　结论的证明

为了完成定理2的证明，先给出下面的引理。

反之，设（1）式成立，则由定理1中4）知

证明 在（1）式中令α=0可知结论成立。

证明 在定理3中令θ=0可知结论成立。

证明 在（2）式中令α=0可知结论成立。

［1］ROBERTS B D.On the geometry of abstract vector space［J］.TÔhoku Math J，1934，39：42-59.

［2］BIRKHPFF G.Orthogonality in linear metric space［J］. Duck Math J，1935，1（2）：169-172.

［3］JAMES R C.Orthogonality in normed linear space［J］. Duck Math J，1945，12（2）：291-302.

［4］SAIDI F B.An extension of the notion of orthogonality to Banach spaces［J］.J Math Anal Appl，2002，267（1）：29-47.

［6］WÓJCIK P.Linear mappings preserving ρ-orthogonality ［J］.J Math Anal Appl，2012，386（1）：171-176.

［8］MOJšKETC B，TURNšEK A.Mapping approximately preserving orthogonality in normed spaces［J］.Nonlinear Anal，2010，73（12）：3821-3831.

［10］ZAMANI A，MOSLEHIAN M S.Approximate Roberts orthogonality［J］.Aequationes Mathematicae，2013，89（3）：529-541.

［11］张芳娟，吉国兴.B（H）上保正交性的可加映射［J］.陕西师范大学学报（自然科学版），2005，33（4）：21-25.

［12］ILIšEVIC D，TURNšEK A.Approximately orthogonality preserving mappings on C*-modules［J］.J Math Anal Appl，2006，318（2）：433-443.

［13］付向红，黎永锦.Banach空间的非常B-正交性［J］.中山大学学报（自然科学版），2008，47（1）：116-117.

［14］ALONSOJ，MARTINIH，WUSL.OnBirkhofforthogonality and isosceles orthogonality in normed linear spaces［J］. Aequationes Math，2012，83（1）：153-189.

［15］孔亮.ε-近似保内积的某个特定值映射［J］.商洛学院学报，2014，28（6）：13-15.

［16］陈超群.保持正交的线性映射［D］.苏州：苏州大学，2013：3-5.

（责任编辑：李堆淑）

Notes on Approximate R-orthogonality

KONG Liang，WANG Nian-liang
（College of Mathematics and Computer Application，Shangluo University，Shangluo726000，Shaanxi）

In a complex normed linear space，it is proved that approximate R-orthogonality is approximate ρ-orthogonality by the definition and properties of norm derivative and the methods of operator theory.Next the definition of weak approximate R-orthogonality is given.It is proved that approximate ρ-orthogonality is weak approximate R-orthogonality under certain condition.

R-orthogonality；approximate R-orthogonality；weak approximate R-orthogonality；approximate ρ-orthogonality

O177.1

A

1674-0033（2016）04-0003-03

10.13440/j.slxy.1674-0033.2016.04.002

2016-04-26

陕西省自然科学基础研究计划项目（2016JM1034）；陕西省教育厅专项科研计划项目（16JK1238）

孔亮，男，陕西商州人，硕士，讲师