淮河上游产沙模拟研究

邹宏荣,王　烨,陆国宾,李琼芳,张　弘,虞美秀,陈芸芸,闫方秀

(1. 河海大学水文水资源学院, 江苏 南京　210098;2. 河海大学国际河流研究所,江苏 南京　210098;3. 河海大学水利水电学院, 江苏 南京　210098)



淮河上游产沙模拟研究

邹宏荣1,2,王烨2,3,陆国宾1,2,李琼芳1,2,张弘1,2,虞美秀1,2,陈芸芸1,2,闫方秀1,2

(1. 河海大学水文水资源学院, 江苏 南京210098;2. 河海大学国际河流研究所,江苏 南京210098;3. 河海大学水利水电学院, 江苏 南京210098)

摘要：以淮河上游息县水文站以上流域为研究区域,将基于网格(1 km×1 km)的新安江模型与土壤侵蚀概念模型集成,构建基于网格的淮河上游泥沙负荷模拟模型,以日为时间尺度,利用息县水文站2000—2008年实测降雨、径流和含沙量等资料,模拟计算得到息县水文站以上流域的泥沙负荷。结果表明,建立的泥沙负荷模拟模型能有效模拟淮河流域产沙过程,且模拟精度较高。研究成果可为淮河上游水土流失治理提供依据,也为其他流域的水土流失模拟提供借鉴。

关键词：淮河上游;土壤侵蚀；含沙量；新安江模型;泥沙负荷

随着人口的急剧增加和科学技术水平的提高,人类正以空前的速度和规模改变着赖以生存的地球环境,地球上水的循环正在发生变化,并引发了一系列环境和生态劣变,如水土流失加剧、水环境恶化、土地荒漠化等,对人类的生存和社会的发展构成了极大的威胁。以我国水土流失为例,2000年水土流失给国家带来的经济损失至少在2 000亿元以上,相当于当年全国GDP的2.25%。因此,水土流失的治理已成为世界各国的重要课题,很多专家学者开展水土流失治理相关方面的研究,包括水土流失模拟。国外已有很多模型对流域水土流失进行预测,具有代表性的有美国农业部提出的SWAT[1-2]模型 (该模型主要应用于水土流失及面源污染模拟、预报)。近年来,美国农业部又提出新一代水蚀预测模型 (WEPP)[3],这是一个土壤侵蚀的物理模型。我国许多学者在流域水土流失方面也开展了大量的研究工作,具有代表性的模型有包为民[4]提出的具有物理概念的土壤侵蚀模型。但是，将广泛应用于我国降雨径流模拟的新安江模型与泥沙侵蚀概念模型进行集成,来模拟流域水土流失过程,这类研究还有待深入。

据《淮河上游水土保持规划》,淮河流域多年的平均土壤侵蚀量为1.58亿t,水土流失面积为20.1万km2,其中上游地区的多年平均侵蚀量为1.08亿t,占全流域土壤侵蚀量的68.4%。因此,开展淮河上游产沙模拟研究十分必要。笔者选择淮河上游息县水文站以上流域为研究区,将新安江模型与土壤侵蚀概念模型进行集成融合,构建基于网格的分布式泥沙负荷模拟模型,根据2000—2008年实测日降雨、日径流和日含沙量等资料,对流域径流量、泥沙负荷时空变化全过程进行模拟,旨在为淮河上游水土流失治理提供依据,为其他流域的水土流失模拟提供参考。

1　泥沙负荷模拟模型构建

1.1产水模拟

本文采用基于网格(1 km×1 km)的新安江模型[5],以3层蒸散发模型计算蒸散发量,以网格作为计算单元[4]进行产流计算,以“先演后合”的汇流计算方法进行汇流演算。坡面汇流采用线性水库法,在计算河道汇流时,将流域划分为25个子流域,将各栅格单元在子流域出水口的总流量按照基于汇流系数的洪水演算法演算至大流域出口,然后在大流域出口断面进行产流和汇流的叠加,最终得到出口断面的流量过程[6]。

1.2泥沙负荷模拟模型的构建

1.2.1产沙模型[7]

根据产沙机制的差异,将流域产沙概化成坡面产沙与沟道产沙,则流域产沙量S为坡面产沙量和沟道产沙量之和:

(1)

式中:SS为坡面产沙量；SG为沟道产沙量；SSi为i时段坡面产沙量;SGi为i时段沟道产沙量;N为时段数;ΔT为时段长。

坡面产沙方程为

(2)

式中:SC为坡面水流挟沙能力;REM为流域平均的抗侵蚀能力;REMM为流域最大的抗侵蚀能力;BS为抗侵蚀能力分布曲线指数;CM为全流域坡面水流的最大可能含沙量,可取常数,也可取变数,主要取决于坡面水流因素变化幅度的大小;R为全流域坡面平均水流深度;A为全流域坡面面积;REC为土壤的抗侵蚀能力;α为抗侵蚀能力小于REC的面积比值;α0为抗侵蚀能力为0的面积比。

沟道产沙量可表示为

(3)

根据拜格诺的河道水流悬移质泥沙公式[8]来推求CG的概念性表达式从而得到SG的表达式:

(4)

式中:CG为沟道水流含沙量;Q为沟道水流流量;CGM为平均沟道产沙浓度;LQ为 ln(Q+1)的时间平均值;BV为常参数。

1.2.2汇沙模型

泥沙的运动是建立在水流运动之上的,而水流中的泥沙含量又能够影响水流的速度,进而影响水流的运动,二者是相辅相成的。因此,参考流域水流的汇流模型,建立流域汇沙模型。汇沙包括坡面汇沙与沟道汇沙两个部分。坡面汇沙和沟道汇沙与水流相似,也存在着泥沙平衡方程和泥沙蓄泄关系。

泥沙平衡方程为

(5)

泥沙蓄泄方程为

(6)

将式(1)进行差分并代入式(2),可得到坡面汇沙方程:

(7)

沟道汇沙方程考虑到河道内泥沙的冲刷和淤积,因此仿照水流分段马斯京根法可得:

(8)

其中

式中:WS为泥沙蓄量;IS为坡面时段产沙量;IS1、IS2分别为坡面时段1和时段2的产沙量;So为坡面时段出沙量;So1、So2分别为坡面时段1和时段2的出沙量;KS为坡面的汇沙时间;CSS为汇沙系数;Sg1、Sg2分别为沟道时段1和时段2的出沙量；Ig为沟道时段产沙量；Ig1、Ig2分别为沟道时段1和时段2的产水得；b0、b1和b2均为过程系数;KES为河段内的泥沙传播时间;XES为泥沙比重系数。

1.3产水与产沙模型的集成融合

河道泥沙演算方程中需要输入河道流入断面和流出断面的流量,笔者将把基于网格(1 km×1 km)的新安江模型模拟计算的流量作为河道泥沙演算方程中的河道流入断面和流出断面的流量,从而实现泥沙负荷模拟模型与新安江模型的集成与融合。

2　泥沙负荷模拟模型在淮河上游的应用

2.1研究区域概况

淮河流域地处我国南北气候过渡带,特殊的过渡性气候和大规模人类活动对地表的强烈扰动,造成了严重的水土流失。研究区息县(图1)以上流域位于东经113°15′～114°46′,北纬31°31′～32°43′,流域面积为10 190 km2,多年平均水面蒸发量800～1 000 mm,多年平均降水量800～1 400 mm,多年平均径流深约371 mm。流域内主要土地利用类型是旱地、林地、水田和灌木丛。对淮河息县水文站1964—2008年的泥沙资料进行分析,发现年水土流失量主要取决于汛期月份降雨量和暴雨出现次数,泥沙负荷汛期(6—9月)占全年的63.4%。以水土流失为载体的面源污染已成为流域上游主要水源区水质污染的重要来源,危及流域水安全与流域生态系统健康。

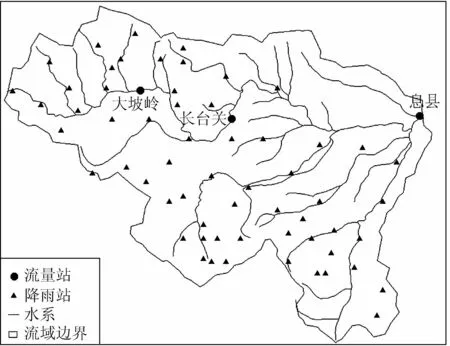
图1　研究区域

2.2资料处理

研究所需数据资料包括地形、土地利用、水文、气象等方面的资料,数据来源与处理方法是:①采用地图投影对模型中输入的所有空间数据的坐标系统进行统一,考虑到研究区域属于中高纬度地区,采用在该地区变形很小的等角横轴割圆柱投影[9],即UTM,Universal Transverse Mercator投影。②地形资料选用美国国家地球物理中心提供的、全球分辨率为1 km×1 km的数字高程数据,运用ArcGIS软件中的掩膜工具,结合流域形状图,切割得到研究流域的数字高程图。③土地利用类型空间分布及面积比例的确定,采用中国科学院提供的2 000 s分辨率为1 km×1 km的土地利用图,结合流域边界,切割得到研究流域2 000 s的土地利用图。

2.3 模型率定和检验

选定2000—2005年为率定期、2006—2008年为检验期,以日为时间尺度对新安江模型和泥沙负荷模拟模型分别进行率定和检验。参数率定结果和模型模拟结果分别见表1～2和表3～4。

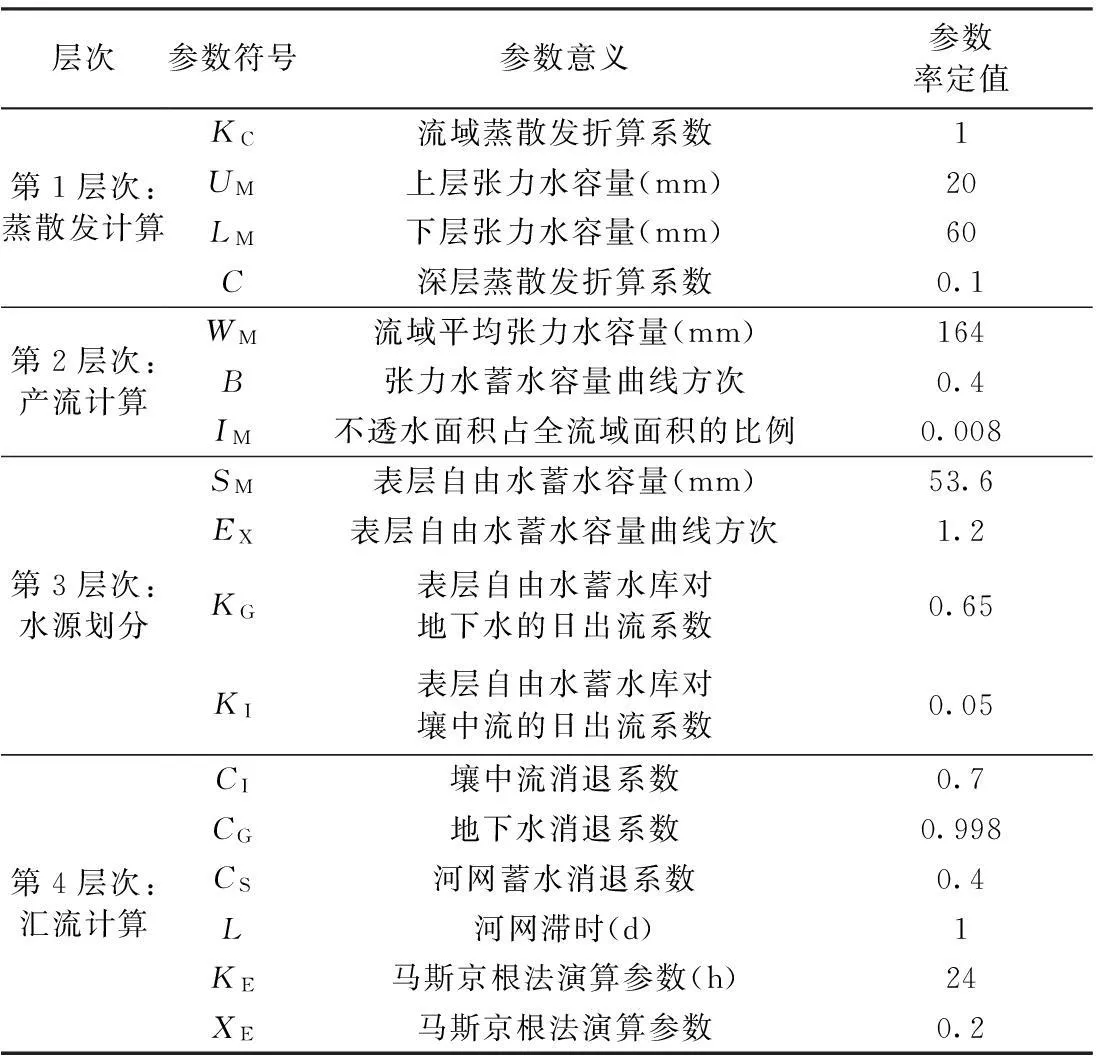
表1　息县流域新安江模型参数率定结果

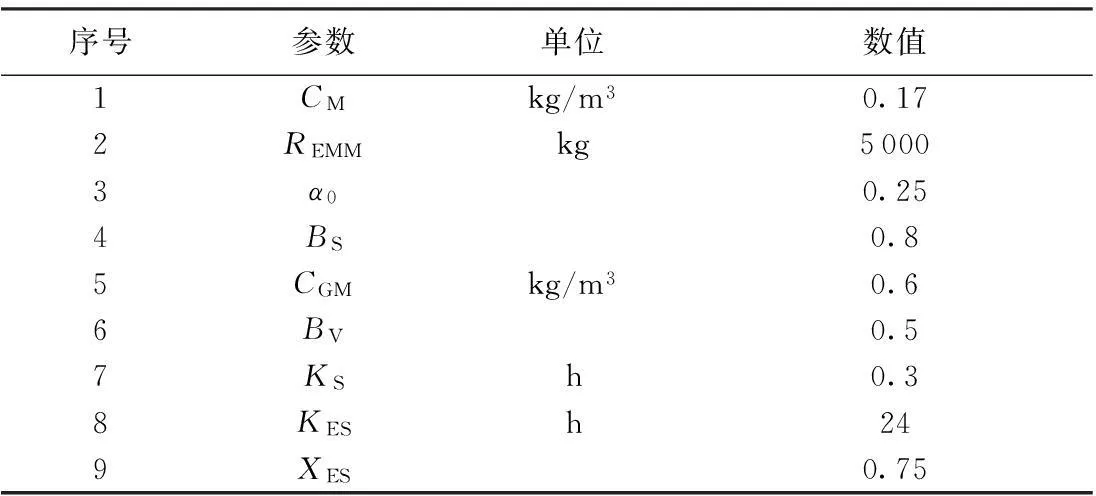
表2　息县流域泥沙模拟参数率定结果

2.4结果分析

表2中各参数的敏感性分析采用比较函数对各参数的敏感度[10]进行分析的方法。本文主要列出CM和CGM的敏感性分析图(其余参数经分析后不敏感,故此处不列出),见图2。由表2可知,流域坡面水流最大可能含沙量CM=0.17 kg/m3,平均沟道产沙浓度CGM=0.6 kg/m3。由图2可知这两个参数的敏感性很强,其微小的改变都能够对结果产生较大的影响,且敏感性随着参数的增大而增大,因此,调整参数时要特别注意这两个参数。

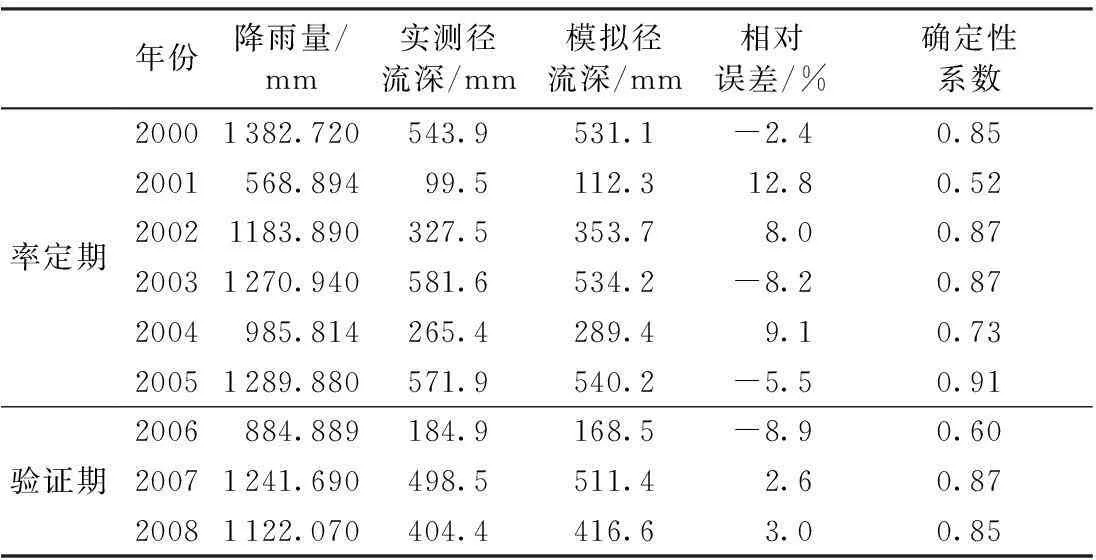
表3　息县流域日径流模拟结果

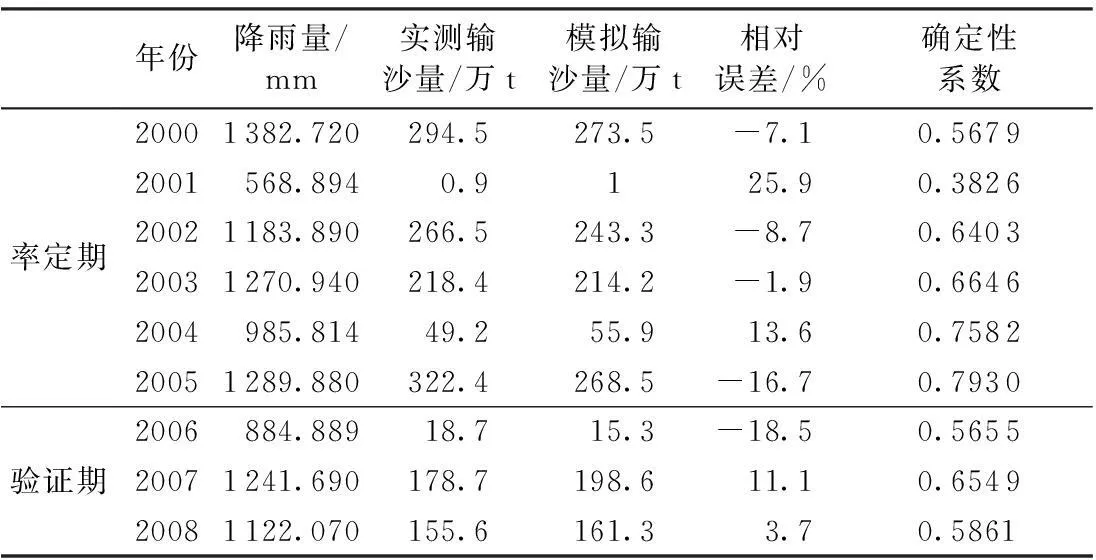
表4　息县流域泥沙日模型模拟结果

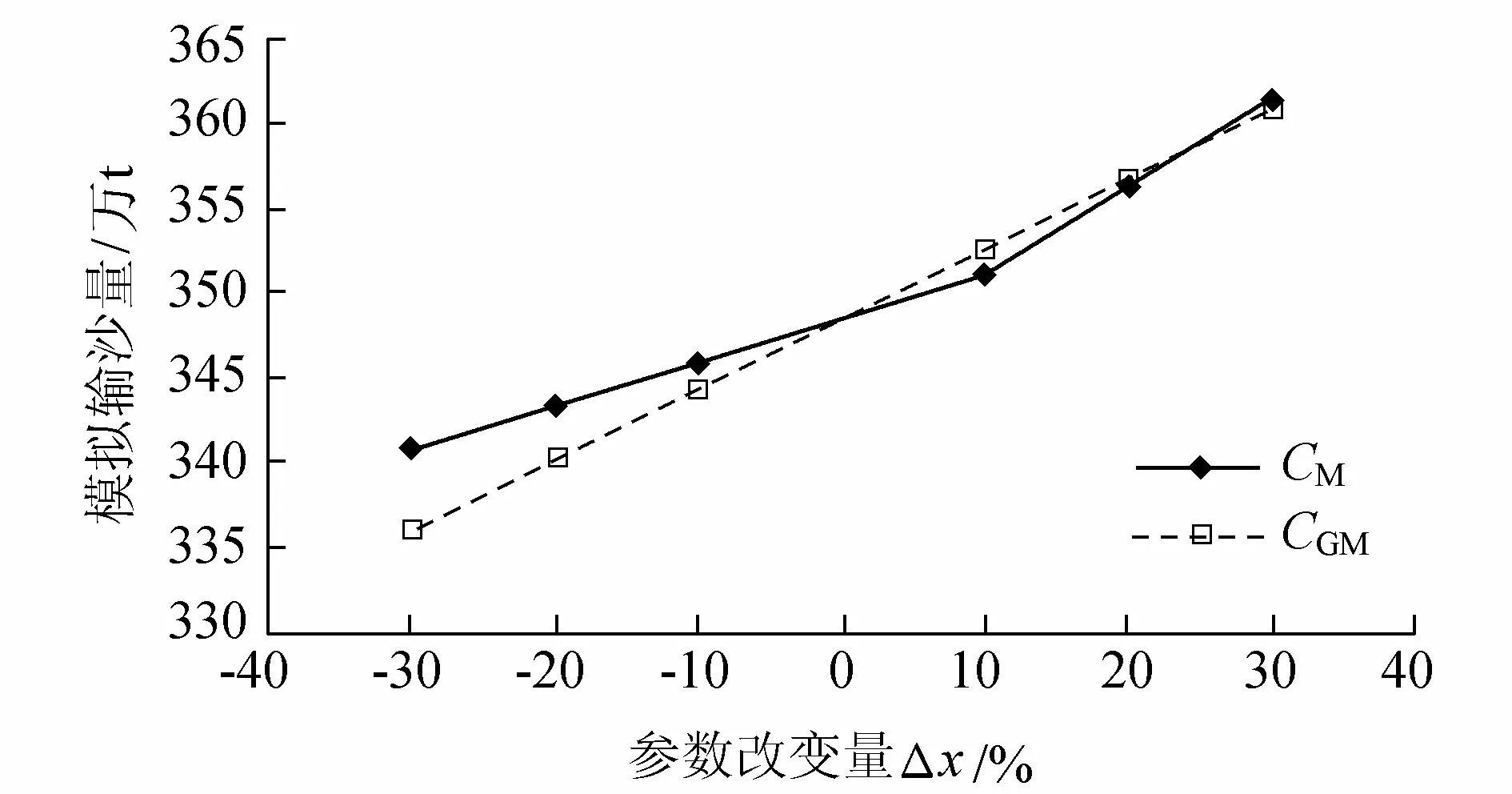
图2　CM和CGM敏感性分析

由表4可知,在率定期与验证期模型模拟的年输沙量的相对误差基本都在20%以内(除2001年以外),确定性系数基本都在0.5以上(除2001年以外)。分析其原因,首先是2001年的降水量仅568.9 mm,小于研究区域多年平均降水量800～1 400 mm,属于来水量较枯年份,在无人类活动对流域进行破坏干扰的前提下,人类对流域每年的需水量相对稳定,但2001年属于来水量较枯年份,在扣除人类的需水量后,来水量更少了,而流域的泥沙运动是建立在水流运动之上的,所以实测输沙量也相应较小,仅0.9万t,远远小于其他年份(流域多年平均输沙量为150万～200万t),因此其相对误差较大,确定性系数较小,属于模拟效果较差的年份,其他年份的模拟结果都能够满足精度要求(相对误差在20%以内,确定性系数大于0.5)。

由图3可知,模型模拟的相关系数为0.98,二者呈强正相关性,表明数据的规律比较可靠,故其日尺度的泥沙负荷模拟可满足泥沙模型的精度要求。

图3　泥沙模拟相关性分析

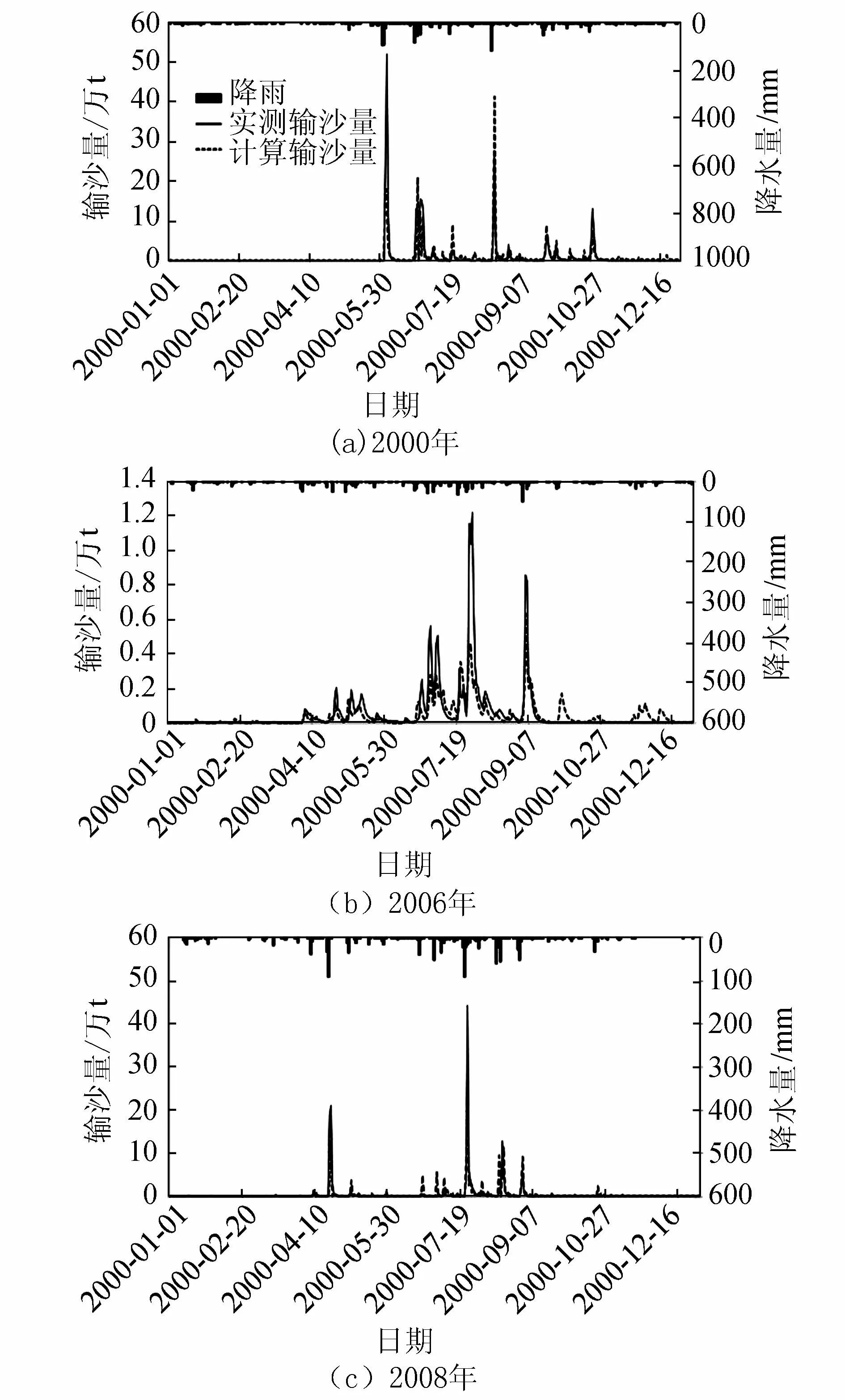
图4　息县以上流域2000、2006、2008年模拟与实测的日输沙量过程线

在本模型中设为常数,但在实际情况下,降雨强度能影响CM值的大小,降雨强度较大的时候,相应的CM值也相应较大,降雨强度与CM之间呈非线性关系。此外,比较表3和表4可知,泥沙模拟结果差于径流模拟结果,这是因为泥沙模拟是建立在径流模拟的基础之上的,径流模拟的误差在泥沙模拟时得到了放大,因此泥沙模拟相对误差会比径流模拟相对误差大。

3　结　语

将新安江模型与土壤侵蚀概念模型进行集成与融合,构建了基于网格的淮河上游泥沙负荷模拟模型，并模拟了淮河上游息县水文站以上流域的泥沙负荷变化过程。研究结果表明,模型参数除CM和CGM比较敏感外,其余参数皆不敏感;在率定期与验证期模型模拟的年输沙量的相对误差基本都在20%以内(除2001年以外),确定性系数基本都在0.5以上(除2001年以外),模型模拟的输沙量与实测输沙量的相关系数为0.98,二者呈强正相关性。可见,日尺度的泥沙负荷过程模拟效果较好,可用于该地区的产沙过程模拟,也可为其他地区的产沙负荷模拟提供参考,为流域水土流失治理和科学资源开发利用提供一定的依据。

参考文献：

[1] NEITSCH S L, ARNOLD J G, KINIRY J R, et al. Soil and water assessment tool user’s manual version 2000[J]. GSWRL Report, 2002, 202：22-26.

[2]王中根,刘昌明,黄友波.SWAT模型的原理、结构及应用研究[J].地理科学进展,2003,22(1):79-86.(WANG Zhonggen,LIU Changming,HUANG Youbo.Principle,structure and application of SWAT model[J]. Journal of Geographical Science, 2003, 22 (1): 79-86. (in Chinese))

[3]张玉斌,郑粉莉,贾媛媛.WEPP模型概述[J].水土保持研究,2004,11(4):146-149.(ZHANG Yubin,ZHENG Fenli,JIA Yuanyuan.Summary of WEPP model[J]. Research of Soil and Water Conservation, 2004, 11 (4): 146-149. (in Chinese))

[4]包为民.水文预报[M].3版. 北京:中国水利水电出版社,2006.

[5]姚成.基于栅格的分布式新安江模型构建与分析[D].南京:河海大学,2007.

[6]李琼芳,谢伟,薛运宏,等.新安江模型在土壤侵蚀模拟中的应用[J].水电能源科学,2010, 28(3): 11-13.(LI Qiongfang,XIE Wei,XUE Yunhong,et al.Xin’anjiang model in the application of soil erosion simulation[J]. Water Research and Power, 2010,28 (3): 11-13. (in Chinese))

[7]包为民.黄土地区流域水沙模拟概念模型与应用[M].南京:河海大学出版社,1995.

[8]BRUNASH J C,FERRAL R L,MCGUIRE A,et al.A generalized streamflow simulation system:conceptual modeling for digital computers[R]. Sacramento,CA:Joliet Federal State River Forecasts Center,1973.

[9]庄卫东,汪春.精准农业中 UTM 投影及反算应用研究[J].黑龙江八一农垦大学学报, 2005, 17(3): 47-50.(ZHUANG Weidong,WANG Chun.Studies on the UTM projection and it’s inverse calculation in the precision agriculture[J].Journal of Heilongjiang Bayi Agricultural University, 2015,17(3):47-50.(in Chinese))

[10]李毅,邵明安,王文焰,等.土壤非饱和导水率模型中参数的敏感性分析[J].水科学进展,2003,14(5):593-597.(LI Yi,SHAO Ming’an,WANG Wenyan,et al.Unsaturated soil hydraulic conductivity the sensitivity analysis of parameters in the model[J]. Advance in Water Science, 2003, 14 (5): 593-597.(in Chinese))

由于篇幅有限,图4只列出2000年、2006年和2008年的模拟与实测的日输沙量过程线。由图4可以看出,模型模拟的计算输沙量存在一个普遍现象,即主峰值上不去。分析其原因,可能是因为参数CM(坡面水流最大含沙量,随着坡面水流流速的变化而变化)

DOI：10.3880/j.issn.1004-6933.2016.04.013

基金项目:国家自然科学基金(41171220);长江学者和创新团队发展计划资助(IRT13062);水利部公益行业经费项目(201001069,201101052)

作者简介:邹宏荣(1990—),男,硕士研究生,研究方向为生态水文及水环境保护。E-mail: 453551965@qq.com 通信作者:李琼芳,教授,博士生导师。E-mail:qfli@hhu.edu.cn

中图分类号：TV143+.4

文献标志码：A

文章编号：1004-6933(2016)04-0080-04

(收稿日期：2015-07-09编辑：彭桃英)

Simulation of sediment yield in upper reaches of Huaihe River

ZOU Hongrong1,2, WANG Ye2,3, LU Guobin1,2, LI Qiongfang1,2, ZHANG Hong1,2,YU Meixiu1,2, CHEN Yunyun1,2, YAN Fangxiu1,2

(1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China;2.InstituteofInternationalRiversResearchAcademy,HohaiUniversity,Nanjing210098,China;3.CollegeofWaterConservancyandHydropowerEngineering,HohaiUniversity,Nanjing210098,China)

Abstract：This study was carried out in the basin located above the Xixian Hydrological Station in the upper reaches of the Huaihe River. A grid-based (1 km×1 km) Xin’anjiang model was coupled with the conceptual model of soil erosion to build the sediment load simulation model for the upper reaches of the Huaihe River. Using the daily measured data of rainfall, runoff, and sediment concentration at the Xixian Hydrological Station from 2000 to 2008, the sediment load in the basin above the Xixian Hydrological Station was calculated. The results show that the built model can be effectively used to simulate the sediment yielding process in the Huaihe Basin, and the model has high precision. This study provides a scientific basis for the control of water loss and soil erosion in the upper reaches of the Huaihe River and provides references for the simulation of water loss and soil erosion in other basins.

Key words：upper reaches of Huaihe River; soil erosion; sediment concentration; Xin’anjiang model; sediment load