基于变邻域搜索算法的物流配送系统集成优化研究

孙 琦戢守峰刘 旭

1（东北大学，沈阳 110169）2（国网辽阳供电公司，辽阳 110099）

基于变邻域搜索算法的物流配送系统集成优化研究

孙 琦1戢守峰1刘 旭2

1（东北大学，沈阳 110169）2（国网辽阳供电公司，辽阳 110099）

本文针对物流配送系统集成优化问题，考虑取货和送货两种业务的配送情形下仓库和车辆的容量上限约束，构建包括仓库的开放成本、配送成本以及容量溢出成本的非线性混合整数优化模型，设计变邻域搜索启发式算法对模型进行求解。算法通过泰森多边形确定位置上的初始订单分配，再通过扫描半径及消费者数据结构标识实现邻域搜索，改进算法对解决方案进行迭代更新，完成优化求解。最后通过对辽宁宅急送取/送一体化物流配送案例进行数值分析，验证算法可行性和有效性。

变邻域搜索算法 取货和送货 非线性混合整数优化模型 集成优化

引 言

“互联网+流通”促使物流行业系统升级，一地多仓和异地多仓问题日益凸显，行业发展具有新模式和新特点，如京东、当当等为提升服务水平自建配送系统，既为消费者提供配送服务，又要满足售后退货的收取服务。物流系统优化问题亟待解决，以满足新时代的行业需求。物流系统的位置/路径集成优化问题研究大体可以分为3个阶段：基础的车辆/路径问题 （Vehicle-Routing Problems，VRP）源自Dantzig等 （1959）的研究，即配送中心为规模有限而需求量不同的消费者提供配送服务 ，满足一定假设约束情况下对有限的配送车辆进行订单分配及路径规划［1］；传统的位置/配给问题 （Location-Allocation Problems，LAP）首次由Cooper（1963）提出，即依据消费者的配送量和交付地点的位置分布关系，规划得出配送区域内配送站的位置和数量规模［2］；近代消费模式的发展促使位置/路径问题 （Location-Routing Problems，LRP）的研究日益显现［3］。如Marinakis （2015）考虑了3种不同的拓扑结构改进粒子群算法优化求解随机需求下固定容量的位置路径问题［4］；Macedo等 （2015）指出构建仓库开放、配送路径和车辆调度的集成问题总成本优化模型，并阐明和标准LRP的主要区别是：每部配送车辆是否可以分配多条路径 ，即车辆和路径之间是否存在一一对应的关系［5］；Torfi等 （2015）针对包含工厂、仓库和客户的三层位置路径集成问题提出采用梯形模糊数来确定评价标准的相对权重，通过工厂和中央仓库的位置选择和客户订单的分配规划，减少物流网络总成本［6］；Vincent等（2014）提出一种改进的模拟退火算法求解开放位置路径问题，并通过数值算例证明改进算法比CPLEX在求解质量和求解时间方面表现更优［7］。Nagy等 （2005）对经典车辆路径问题进行扩展，考虑客户取货和送货情况下的单一仓库和多仓库集成模型 （Vehicle Routing Problem with Pickups and Deliveries，VRP-PD），并用交替启发式算法进行了近似求解［8］；Polat等 （2015）基于扰动的邻域搜索算法求解VRP-PD问题［9］；Wang等 （2015）指出带时间窗的取货和送货车辆路径问题 （VRPSPDTW）为NP-hard问题 ，并用p-SA元启发式算法求解［10］；Liu等 （2013）构建医疗系统的车辆路径物流调度模型 ，设计两个元启发算法 （禁忌搜索和遗传算法）进行求解，配送系统总成本得到优化［11］；Li等 （2015）设计自适应邻域搜索算法求解同时取货和送货的多仓库车辆路径问题［12］。

近年，国内学者对物流配送系统集成问题也做出探索。如李群霞等 （2015）研究了二级供应链联合优化问题，并设计了解决方案［13］。唐金环等 （2015）考虑时间和碳排放约束下的车辆路径优化问题，构建了非线性混合整数规划模型，并用粒子群算法对物流配送系统进行决策求解［14］；唐金环等 （2014）设计BFA-PSO算法求解选址——路径——库存集成问题［15］；李富昌 （2016）研究了库存运输联合优化模型，决策中心联合做出订货量、零售价和营销成本的决策，再给出库存运输联合优化最优策略的求解方法［16］；王超等（2014）提出模拟退火算法求解带时间窗的取货和送货车辆路径问题 （VRPSPDTW）［17］。

综上所述 ，迄今为止的研究表明：对于车辆路径经典问题的研究，随着时代发展具有新的特点；VRP问题的研究成果日益显现，而对于LRP问题扩展成果还很鲜见；车辆位置路径问题往往采用启发式算法进行求解，对于智能算法的研究有待丰富。本文在LRP问题基础上进行扩展，考虑取/送一体化的订单分配与物流配送集成优化问题 （Location Routing Problem with Pickups and Deliveries，LRP-PD）模型构建，并设计启发式算法进行求解。

1 问题描述与符号说明

1.1 问题描述

LRP-PD可抽象为一个完全有向图G=｛N，E｜Nw∈N，Np∈N，Nd∈N；｛i→j｝∈E｝，其中Nw表示已知库存容量的仓库结点，需求不确定的消费者分为两类结点Np表示取货消费者结点，Nd表示送货消费者结点；车辆结点M=｛Mp，Md｝。集成配送系统中，每个车辆完成取货和送货服务之后，返回到相同的开放仓库。消费者在一个订单周期内仅分配一辆车提供服务，车辆完成服务后返回仓库。决策者对集成配送系统进行优化时，需选择开放哪些仓库，确定车辆的配送路径，以降低整个系统的运作成本。

一般情况下，消费者需求是不确定的，决策者为配送系统预先设计先验路线方案，以便选择最佳配送路线降低成本 ，而车辆容量是决定规划方案中路线数量的主要因素。消费者随机需求符合泊松分布特征，因此将取货和送货的先验路线方案分别表示为两组时间序列：θ=｛θ0，θ1，θ2，…，θκ，… ，θn，θ0｝和θ=｛θ0，θ1，θ2，…，θκ，…，θn，θ0｝，其中θκ表示组成配送路径结点的时间序列结点，车辆从初始开放仓库θ0=n出发，最后返回起点仓库交车。为了简化问题 ，定义v和v为消费者随机需求变量产生的货物容量，参数λp和λd分别为取货和送货上限概率，即P（v＞V）≤λp和P（v＞V）≤λd。消费者取/送货物β的均值路径序列｛μ，μ，… ，μ｝和｛μ，μ，… ，μ｝，则v和v的均值分别为

1.2 符号与参数

模型中所用参数变量和决策变量总结如表1：

表1 符号说明

2 成本优化数学模型

系统优化的目标是总成本最小化。本文将集成系统的总成本模型分解为3个子问题进行构建：仓库开放成本，配送运输成本和容量损失成本。系统优化的数据结构表示为：LRP-PD=｛xw，yiw，z｜C｝。随机需求到达后，系统根据消费者总需求情况进行订单分配，规划配送仓库完成订单交付，产生仓库运营成本。而配送运输成本和容量损失成本之间存在交集，因此将容量损失过程分为车辆运输容量溢出和仓库容量溢出。

2.1 配送运输成本

由于消费者需求是不确定的，当发货需求相对车辆固定容量溢出时，每辆车遍历消费者结点数受取货上限概率约束。取货配送路径θκ上，容量溢出结点的数量小于等于1时，单辆车取货容量溢出成本。其中C和C分别表示取货时车辆容量溢出，车辆从仓库n到溢出点θκ之间的往返成本。进一步地，得到所有车辆整条取货路径上发生容量溢出的预期成本；同理 ，可推导出配送系统送货过程的容量溢出成本。

2.2 仓库容量溢出成本

由于需求的不确定性，仓库发生容量溢出的情况可能存在，一旦这种情况发生，物流配送系统就会产生额外转运成本。货物β存入仓库每超出一单位容量记为ρ，产生额外处理仓库存储过剩的单位成本cβ。由此，得到仓库溢出成本：

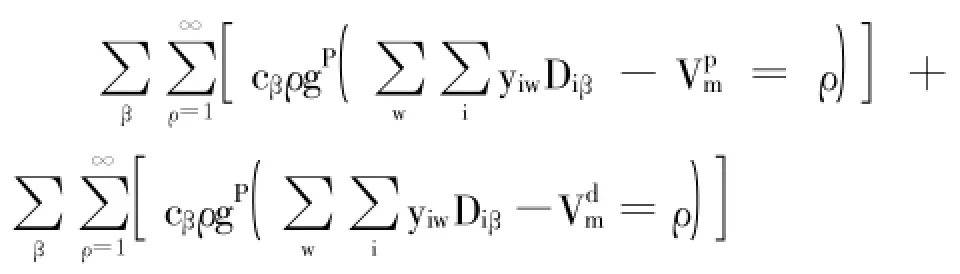
其中，任何一类货物β对于仓库w存在一个超过仓库容量的概率，消费者需求是一个随机变量，同时每单位产生额外仓库容量溢出费cβ。进而得到每批货物β的所有预期仓库容量溢出成本总额。

2.3 配送集成系统的非线性混合整数规划模型综上，成本优化数学模型表示为：

其中，式 （1）是考虑取货和送货一体化的物流配送集成系统优化的目标函数，等式右边求和分量分别表示仓库运营成本、路径运输成本、车辆取货固定成本、车辆送货固定成本、取货车辆容量溢出成本、送货车辆容量溢出成本、取货造成的仓库容量溢出成本和送货造成的仓库容量溢出成本。

约束部分：由于每位消费者需求的不确定性，取货和送货车辆荷载的概率分别不超过车辆容量上限概率λp和λd，得到式 （2）和式 （3）的车辆容量约束。式 （4）和式 （5）确保每位消费者都被规划一条配送路径，并且只有一个前端配送路径结点。式 （6）～式 （9）表示每条路径连续性的约束 ，保持起止仓库为同一仓库。式 （10）和式（11）表示消除子回路。式 （12）和式 （13）表示路径上的仓库是开放的 ，可进行订单分配满足消费者需求。式 （14）～式 （16）表示决策变量为0 ～1变量。

综上所述，LRP-PD是LAP和VRP的组合变体，二者均为NP-hard，因此LRP-PD也是一个NP-hard问题。然而，由于其涉及 FLP、VRP、不确定需求和取/送货路线的物流配送系统集成问题，使得LRP-PD更为复杂。本文针对这一问题，提出一种近似求解的启发式算法。

3 变邻域搜索算法过程设计

以辽宁宅急送在一个订单周期内15个配送仓库构成的取/送一体化物流配送系统为研究案例，优化流程如图1所示。将LRP-PD分解成3个子问题：仓库分配问题，订单分配问题和车辆路径规划问题。仓库开放后，分配消费者订单，确定车辆配送路径。下面研究各个子问题的解决方案如下。

3.1 仓库分配

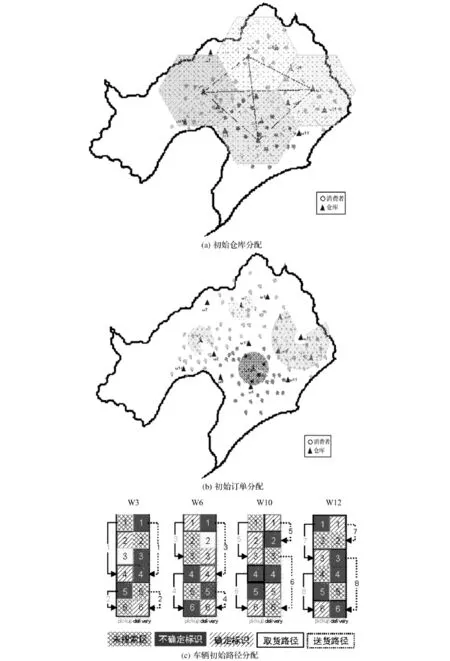
图1 取/送一体化物流配送系统集成优化过程图

首先需要确定开放仓库的数量。对于传统的LRP问题，根据消费者总需求可估算出开放仓库的数量，而本文研究的是消费者需求不确定情形。一般情况，总取/送货容量超出的配送系统容量上限时，额外增加仓库容量溢出成本，因此有必要分配更多的仓库。另一方面，仓库和车辆未被利用的容量增加了机会损失成本，开放仓库的数量越少则成本越低。为解决这个问题，引入参数γpβ和γdβ分别表示取/送货物β时，配送系统分配的仓库数量；ξpβ和ξdβ表示所有需要取/送货物β的随机需求。配送系统分配的开放仓库数量κpβ和κdβ取值范围受到仓库容量上限概率常量λw及仓库平均容量Vw的限制，即对货物β的最低配送量P （ξpβ＞Vwgγpβ）≤λw和P（ξdβ＞Vwgγdβ）≤λw。配送货物的数量按容量大小分类记为η，记配送系统开放仓库κ=max｛κp1，κd1，κp2，κd2，… ，κpη，κdη｝是最优解集中的最大值，开放仓库的数量应该在κ值附近。

如图1（a）所示，初始种群集合（w1，w3，w6，w10）为开放仓库的初始解，确定开放的仓库数量及初始值。如果w3被w8代替，开放仓库更新分配为（w1，w8，w6，w10）。为了搜索到更好的开放仓库组合，确定仓库替换算子为两个仓库之间位置距离相等的仓库。替换算子可以替代产生得到两个分组。例如，图中的仓库w9位于与w3和w10等距点，所以它可以代替这两组，即（w1，w9，w6，w10）和（w1，w3，w6，w9）是解决方案过程中开放仓库组合的一个有效组合。

3.2 订单分配

一般情况，开放的仓库可以为与其距离相对最近的客户提供较好的服务，运输成本相对较低。消费者收货过程需得到一个开放仓库提供的服务，LRP-PD可视为一个集合覆盖问题。

初始分配能够把客户分成s组，而容量和运输路径的约束会使订单分配情况改变。因此，依据模型特点设计更新方法如下：消费者被分为两个集群，即靠近仓库集和远离仓库集。如果一个消费者到一个仓库的距离小于r，则分配和初始分配保持不变，被称为分配确定；否则，消费者被标记为分配不确定，这意味着它的分配是可以改变的。图1（b）说明了分配确定和分配不确定组的边界。因此，当搜索半径越小的时候，更多的分配不确定的消费者会出现，这会使自由度和解域更大。更新算子通过调整订单分配，使模型满足仓库容量约束，相对扩大搜索解域的范围。

3.3 车辆路径分配

由于车辆订单交付地点具有散乱性，本文改进变邻域搜索 （Variable Neighborhood Search，VNS）算法以解决VRP。Mladenovic＇等人 （1997）提出的变邻域搜索是一种用于优化求解的邻域搜索元启发式算法［20］。Jarboui等 （2013）［21］，Hemmelmayr 等 （2015）［22］和Coelho等 （2015）［23］研究并扩展了变邻域搜索求解位置路径问题，改进邻域搜索规则使得搜索过程尽可能高效地靠近解域。

图1（c）显示了标记为w3、w6、w10和w12的4个开放仓库的拟解决方案。每个仓库标记两列标识：左列为需取货消费者，右列为需送货消费者。数字标记车辆的配送服务顺序，进而形成配送路径。根据车辆的容量约束，如前文所述，订单分配确定消费者集合是不变的；不确定消费者可以被任何仓库提供服务。因此，在本文中构建了一个初始的解决方案，通过在分配仓库的数字序列中插入分配确定消费者来表示；同时随机插入分配不确定消费者到任意的序列中。

引入短期记忆数据结构实现邻域搜索半径r的控制，避免指针搜索移动到一个循环周期内已经访问过的解决方案。同时，设计一个中长期记忆的数据结构，即一个线性链表，为实现搜索空间更靠近最优可行领域，标记不可行邻域，提高效率。在解邻域搜索中，本文的改进算法引入交换和移动算子：交换算子，即在同一个操作 （取货/送货）下，两个消费者结点的交换，一个分配确定的消费者不能与属于不同仓库的消费者交换，则只有分配不确定消费者可以在不同的仓库之间进行交换；移动算子，即一个消费者订单从当前位置转移到另一个位置。只有分配到不确定消费者的订单才允许移动到当前序列外的位置 ，则分配确定消费者的订单只能在当前序列中移动。

图2描述改进的邻域搜索算法实现流程图。由配送量下界确定初始开放仓库的数量，进而确定初始解决方案，即搜索的起始集，通过交换算子和移动算子扩大搜索域。κ=max｛κp1，κd1，κp2，κd2，…，κpη，κdη｝是对解决方案的放松，因此仓库的数量可能被放大。在流程图中，为了获得开放仓库的最佳数量，求解过程被执行κ-1次，直到无可行的解决方案。

4 实验结果

案例配送系统架构如图3所示，实验平台Matlab6.0。随机抽取100个消费者订单样本，成本参数范围：Cw∶U［2000，8000］，w∈［1，15］，C～U［200，500］，C～U［200，500］，C～U［0，5000］，C～U［0，500］；容量范围：V～U［10t，30t］，V～U［20t，50t］，V～U［0，5t］，V～U［0，5t］。

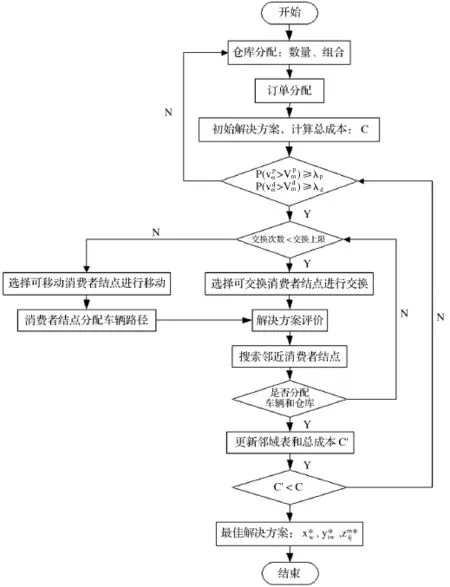
图2 集成系统优化的邻域搜索算法流程图

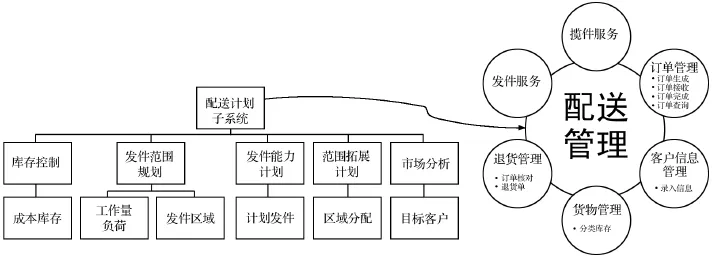
图3 宅急送系统功能模块图

由于各子仓库分布在省内各地，仓库开放成本受当地经济因素影响呈现均匀分布，具有梯度变化，如表2所示。

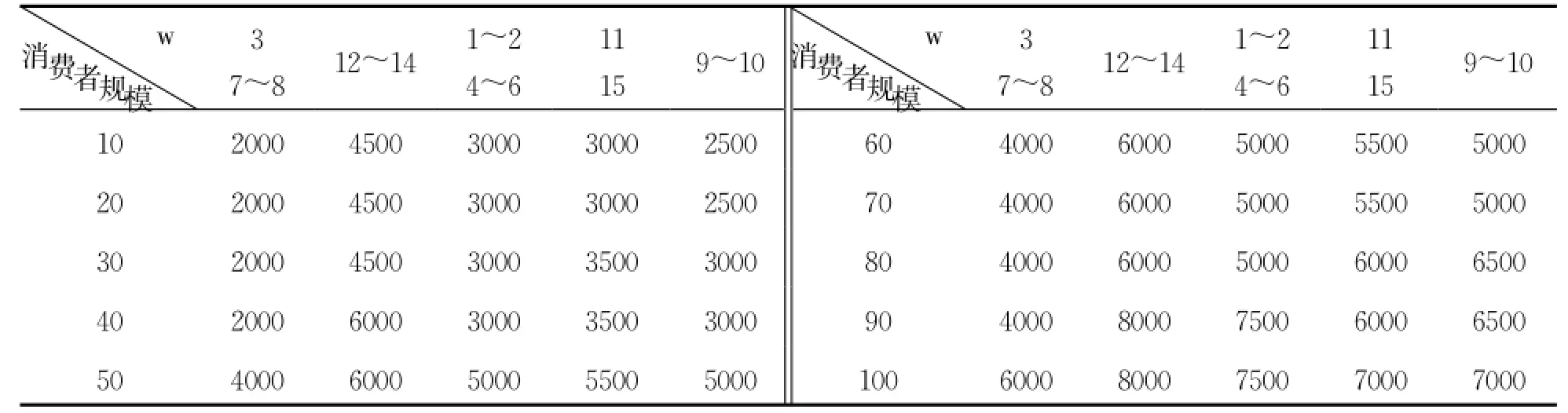
表2 消费者规模与仓库开放成本变化梯度表 元

配送车辆按照载重与耗油量特征，分为大型车、中型车和小型车。为更好满足消费者订单需求，充分利用已有数据资源，提高配送系统集成优化程度，依据订单样本密集程度选择车辆类型。路径优化结果如图4所示。

图4 订单样本配送路径优化结果

由图4（a）可见，经过有限次的迭代，变邻域搜索得到最优的订单分配路线。图4（b）所示当前最优解值靠近最优解。

将样本集进行4种情形优化效果对比，如表3所示，以测试本文改进的变邻域搜索算法。对比样本集合在没有考虑集成优化、单一仓库分配成本优化、仓库——订单分配集成及仓库——订单——路径集成情况下，运作总成本、误差率和运行时间的差异随着模型复杂度增加，运算时间增加及总成本降低程度明显。

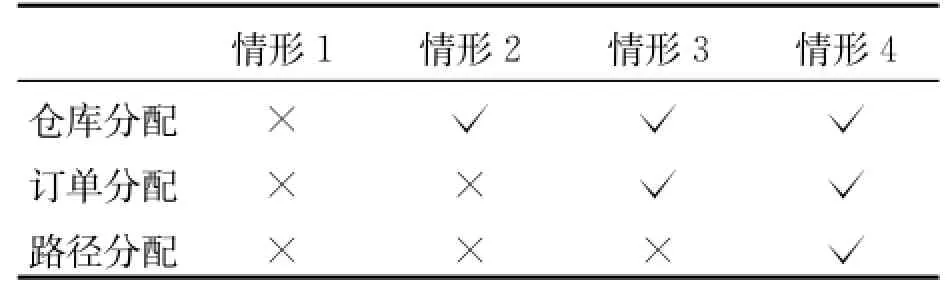
表3 算法测试情形设计

5 结束语

本文考虑了物流配送系统从订单接收到订单交付的整个运营过程，构建了随机需求下物流系统成本优化模型。为优化系统的总成本，模型从3个运作阶段进行成本核算：仓库开放过程，运输过程和容量损失过程，并对各子阶段的运营成本进一步细化建模。

配送集成系统优化模型的求解过程分成以下步骤：（1）仓库分配：确定集成系统分配仓库的数量；（2）订单分配：确定消费者订单配送的范围；（3）车辆路径分配：控制搜索半径，对消费者结点进行变邻域扩充。数值案例的实验结果表明，通过有限次的迭代计算，系统总成本优化显著，节省成本约占未优化成本的13%，充分证明了本文优化模型的可行性和算法的有效性。

进一步地，在模型构建与求解中得到经济管理学启示如下：（1）在数据资源日益丰富的环境下，企业对自建物流体系的优化决策过程应充分利用互联网和智能技术降低运营成本，进而提升物流行业的流通效率；（2）对复杂物流系统的优化过程，采用适当的研究手段进行问题分解与集成，能够为决策者提供更精确的计算结果和更有价值的决策参考；（3）车辆和仓库的容量动态影响配送系统成本优化，因此在实践中挖掘有效的问题影响因素可以提升模型的优化效果。

本文研究尚有改进之处，如在未来研究中扩大系统集成要素和问题规模，优化预处理过程和算法设计过程，以提高算法的运行时间和运行精度。

［1］Dantzig G B，Ramser J H.The Truck Dispatching Problem ［J］.Management Science，1959，6（1）：80～91

［2］Cooper L.Location-allocation Problems ［J］.Operations Research，1963，11（3）：331～343

［3］Min H，Jayaraman V，Srivastava R.Combined Location-routing Problems：A Synthesis and Future Research Directions ［J］.European Journal of Operational Research，1998，108（1）：1～15

［4］Marinakis Y.An Improved Particle Swarm Optimization Algorithm for the Capacitated Location Routing Problem and for the Location Routing Problem with Stochastic Demands ［J］.Applied Soft Computing，2015，37（C）：680～701

［5］Macedo R，Alves C，Hanafi S，et al.Skewed General Variable Neighborhood Search for the Location Routing Scheduling Problem ［J］.Computers&Operations Research，2015，61：143～152

［6］Torfi F，Farahani R Z，Mahdavi I.Fuzzy MCDM for Weight of Object's Phrase in Location Routing Problem ［J］.Applied Mathematical Modelling，2016，40：526～541

［7］Vincent F Y，Lin S Y.A Simulated Annealing Heuristic for the Open Location-routing Problem ［J］.Computers&Operations Research，2015，62：184～196

［8］Macedo R，Alves C，Hanafi S，et al.Skewed General Variable Neighborhood Search for the Location Routing Scheduling Problem ［J］.Computers&Operations Research，2015，61：143～152

［8］Nagy G，Salhi S.Heuristic Algorithms for Single and Multiple Depot Vehicle Routing Problems with Pickups and Deliveries［J］.European Journal of Operational Research，2005，162（1）：126～141

［9］Polat O，Kalayci C B，Kulak O，et al.A Perturbation Based Variable Neighborhood Search Heuristic for Solving the Vehicle Routing Problem with Simultaneous Pickup and Delivery with Time Limit［J］.European Journal of Operational Research，2015，242（2）：369～382

［10］Wang C，Mu D，Zhao F，et al.A Parallel Simulated Annealing Method for the Vehicle Routing Problem with Simultaneous Pickupdelivery and Time Windows［J］.Computers&Industrial Engineer－ing，2015，83：111～122

［11］Liu R，Xie X，Augusto V，et al.Heuristic Algorithms for a Vehicle Routing Problem with Simultaneous Delivery and Pickup and Time Windows in Home Health Care［J］.European Journal of Operational Research，2013，230（3）：475～486

［12］Li J，Pardalos P M，Sun H，et al.Iterated Local Search Embedded Adaptive Neighborhood Selection Approach for the Multi-depot Vehicle Routing Problem with Simultaneous Deliveries and Pickups ［J］.Expert Systems with Applications，2015，42（7）：3551～3561

［13］李群霞 ，马风才，张群.供应链提前期供需联合优化库存模型研究 ［J］.中国管理科学，2015，23（4）：117～122

［14］唐金环 ，戢守峰，沈贵财.时变网络下考虑碳排放的车辆路径优化 ［J］.系统工程，2015，33（9）：37～44

［15］唐金环 ，戢守峰 ，朱宝琳.考虑碳配额差值的选址-路径-库存集成问题优化模型与算法 ［J］.中国管理科学 ，2014，22（9）：114～122

［16］李富昌.考虑营销成本的库存与运输联合优化三阶段决策模型研究 ［J］.工业技术经济，2016，（2）：39～44

［17］王超，穆东.基于模拟退火算法求解VRPSPDTW问题 ［J］.系统仿真学报 ，2014，26（11）：2618～2623

［18］郭庆军，等.制造业与物流业种群生态系统协同演化实证研究 ［J］.工业技术经济 ，2014，（7）：9～17

［19］Park S J，Cachon G P，Lai G，et al.Supply Chain Design and Carbon Penalty：Monopoly vs.Monopolistic Competition ［J］.Production and Operations Management，2015，24（9）：1494～1508

［20］Mladenovic＇N，Hansen P.Variable Neighborhood Search ［J］.Computers&Operations Research，1997，24（11）：1097～1100

［21］Jarboui B，Derbel H，Hanafi S，et al.Variable Neighborhood Search for Location Routing［J］.Computers&Operations Research，2013，40（1）：47～57

［22］Hemmelmayr V C.Sequential and Parallel Large Neighborhood Search Algorithms for the Periodic Location Routing Problem ［J］.European Journal of Operational Research，2015，243（1）：52～60

［23］Coelho I M，Munhoz P L A，Ochi L S，et al.An Integrated CPU-GPU Heuristic Inspired on Variable Neighbourhood Search for the Single Vehicle Routing Problem with Deliveries and Selective Pickups ［J］.International Journal of Production Research，2015：1～18

A Logistics System Integrated Optimization with Variable Neighborhood Search Algorithm

Sun Qi1Ji Shoufeng1Liu Xu2
（1.Northeastern University，Shenyang 110169，China；2.State Grid Liaoyang Electric Power Supply Company，Liaoyang 110099，China）

In order to optimize logistics integration system by the action plan for“Internet Plus Circulation”，a nonlinear mixed integer model is proposed to reduce total cost including open warehouse cost，distribution cost and capacity overflow cost，which contains two kinds of trade business：pickup and delivery for consumers.Variable neighborhood search heuristic algorithm is designed to solve the model and Tyson polygon is used to determine the initial order allocation in pretreatment process from the perspective of geographical space.Then it also designs some of the data structures to record the result and running attributes of the neighborhood searching by scanning radius so that the improved algorithm can update iterative solutions and get the optimal solution.In the end，the effectiveness of the models and algorithms are testified through the numerical example from the project of an express delivery company in China's Liaoning province.The research results show that reasonable use of big data planning can improve operational efficiency of the traditional logistics mode.

variable neighborhood search algorithm；pickups and deliveries；mixed integer nonlinear optimizationmodel；integrated optimization

（责任编辑：史 琳）

10.3969/j.issn.1004-910X.2016.08.006

F224

A

2016—04—14

国家自然科学基金资助项目 “碳限制与行为约束下多源选址——路径——库存集成模型研究”（项目编号：71572031），辽宁省教育厅人文社科基地项目 “低碳化多源选址——路径——库存问题联合优化模型与算法研究”（项目编号 ：ZJ2013014）。

孙琦，东北大学工商管理学院博士研究生。研究方向：物流系统建模与优化、复杂网络分析。戢守峰，东北大学工商管理学院教授 ，博士生导师。研究方向：物流系统建模与优化、物流与供应链管理。刘旭，国网辽阳供电公司硕士研究生。研究方向 ：企业标准化管理、管理创新、品牌管理。