向量式有限元桁架结构并行程序节点分配技术

杜庆峰， 吴　瀚

(同济大学 软件学院， 上海 201804)



向量式有限元桁架结构并行程序节点分配技术

杜庆峰， 吴瀚

(同济大学 软件学院， 上海 201804)

摘要：结合向量式有限元(VFIFE)的计算规则以及桁架结构的特点，提出了一种并行程序节点分配机制.通过对桁架结构模型数据的分析，定义模型数据的分解规则，动态实现对模型数据的分解.依据分解的结果来动态划分并行计算的数据集，并且基于特定的并行计算框架完成并行计算.实例验证表明，该节点分配机制是有效的，并且极大地提高了计算效率.

关键词：向量式有限元(VFIFE)； 桁架结构； 并行算法

1　研究背景及问题的提出

1.1背景介绍

随着计算机科学的迅速发展，计算科学、分析理论和物理实验构成了现代科学发展的三大支柱.在建筑工程领域，结构力学、有限元理论是目前主流的分析架构，这种架构主要包括两部分：为了描述结构体的性质和物理行为设定一组描述参数；为了进行数值分析而提出的一组行为变化准则及简化假设.依据此架构，工程师们可以通过数学方法来模拟一个结构，规划计算流程，得到结构上任意一点的位置变化，以及其他力学参数.

向量式有限元(VFIFE)[1-3]是由美国普渡大学丁承先教授提出的结构行为分析的一个创新概念.VFIFE是求解结构的大变形、大变位、弹塑性、碰撞、倒塌等非线性或不连续力学行为的新方法.以此理论为基础，可以通过简单的而系统化的计算程序对结构的真实行为进行仿真.

VFIFE的研究与应用尚处于起步阶段，对许多实际问题的模拟还比较初步.尽管如此，在许多方面的应用尤其是涉及多个结构体的系统动力、大变形等问题的处理上，VFIFE已经显示出了独特的优越性，即程序的稳定性、计算的收敛性与准确性、程序编写的简洁性以及适合并行处理等一系列优点，且无需集成整体刚度矩阵[4]，具有更高的程序开发效率.

空间桁架结构是建筑工程领域常见的一种格构化梁式结构.常用于大跨度的厂房、展览馆、体育馆和桥梁等公共建筑中.本文将以桁架结构为研究对象，实现VFIFE程式计算过程的并行化处理.

1.2VFIFE计算过程的不足及问题的提出

1.2.1VFIFE计算过程

VFIFE计算过程分可为3个模块：前处理模块、程式计算模块、后处理模块.结构体的模型数据通过前处理模块生成并解析，输入到程式计算模块进行计算，最终输出可由后处理模块进行展示的行为数据.流程图如图1所示.

前处理模块中，通过建模生成的数据即VFIFE程序计算的输入数据，由第三方建模软件SAP2000导出的模型文件转换而来.以桁架结构为例，桁架是一种由杆件在两端用节点连接而成的结构，因而模型数据主要包括三部分：node、element、force，分别包含了节点信息、杆件与节点的拓扑信息以及外力信息.

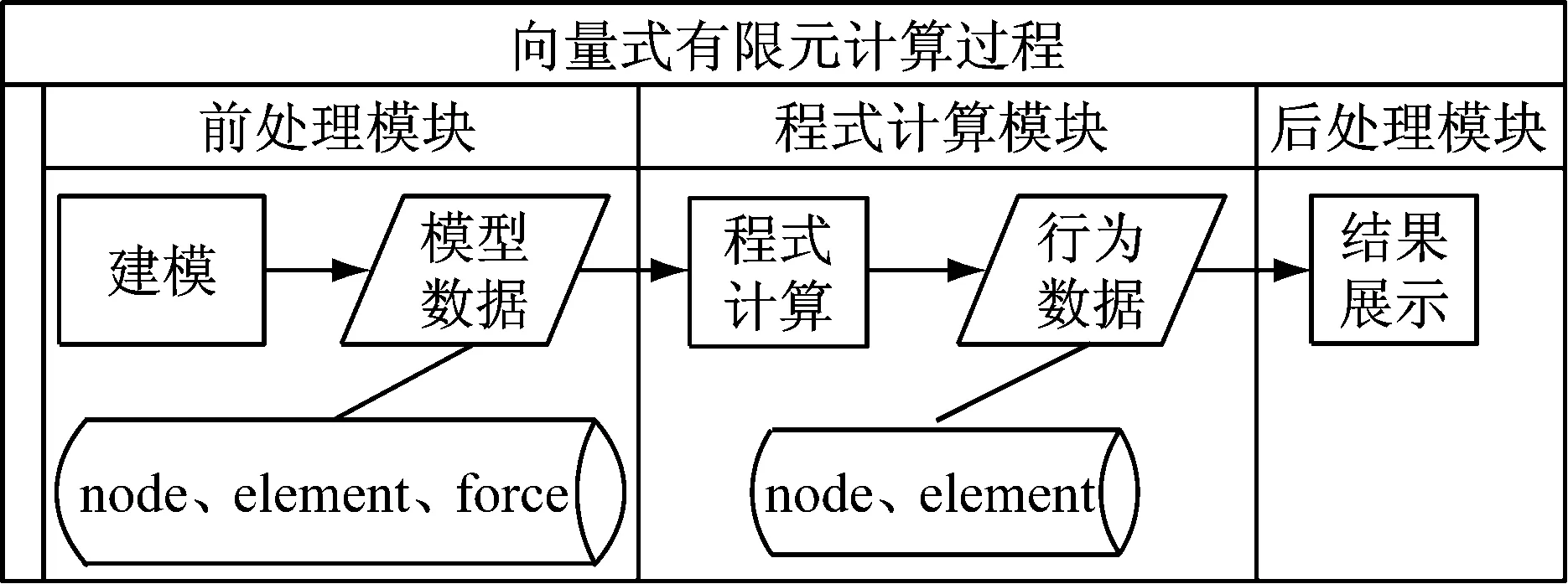
图1　VFIFE计算流程图

模型数据的节点信息node每一行代表一个节点，包含了节点的编号值、节点的类型(铰接点或刚节点)、节点的坐标信息以及节点的质量，例如：

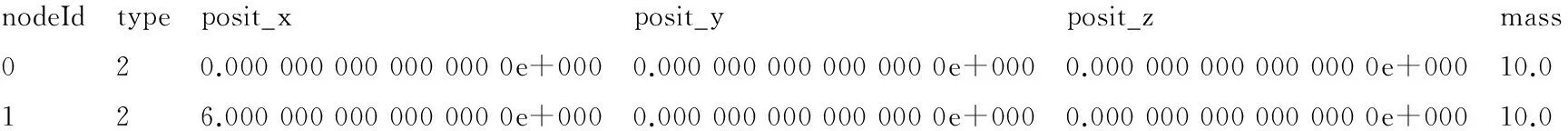
模型数据的杆件信息element每一行代表一个杆件，包含了杆件的编号值、杆件两端节点编号值以及杆件的一些力学参数(杨氏模量、横截面积、密度和极限力)，例如：

模型数据的力学信息force每一行代表一个作用力，包含了力的编号值、类型(默认为集中力)，力的作用位置、方向以及作用时间，例如：

程式计算模块中，计算程序依据桁架结构模型的位移迭代公式编写，将前处理模块生成的模型数据作为第一帧输入，由节点当前帧以及上一帧的位置计算出该点下一帧的位置.该位移迭代公式可简写为

(1)

式中：Xn+1、Xn及Xn-1依次为节点下一帧坐标向量、节点当前帧坐标向量以及节点上一帧坐标向量；C1、C2及C3均为与结构模型本身相关的力学常量；Fn则表示节点当前帧所受的外力、作用力等.

后处理模块中，行为数据即程序计算的输出数据，由程式计算程序直接导出，描述了外力作用下结构模型的变形行为，分为两部分：时间信息的几何模型数据Node.txt和包含时间信息的拓扑模型数据Element.txt.

行为数据中几何模型数据包括了帧、节点编号值、节点的坐标信息，例如：

行为数据中拓扑模型数据包括了帧、杆件编号值、杆件两端的节点编号值，例如：

后处理行为数据可直接用于展示结构模型的动画效果，后处理模块的程序可以根据每一帧的行为数据绘制出模型，并连续地展示出来.行为数据规模与结构模型的大小、演示时间帧数量成正比.

1.2.2问题的提出

现阶段，前处理模型数据均来源于传统的有限元分析工具(SAP2000、ANSYS等)建模导出的模型数据文件，然而这些建模软件封装度高，没接口支持，算法灵活性差，导出的模型数据文件无法直接用于VFIFE程序计算.

在程式计算模块，程序代码处理海量数据时，仍然是逐点依次进行迭代运算，需要等所有节点一次迭代完成，再进行下一次迭代运算，因而计算效率不高，且无法体现VFIFE适合并行处理等优势.

在后处理模块，后期的数据读取与行为分析显示也已经完成，通过调用OpenGL库，整个有限元分析过程可以以三维动画的形式展示在用户面前[5].此外，杜庆峰等[5-6]提出的压缩模型及算法为数据文件的云端存储提供了可能，具有很高的实用性.

针对以上不足，有必要进行VFIFE行为数据的并行分布式处理研究，这对于推广VFIFE这一新型结构力学方法，实现高性能的并行有限元分析系统具有重要意义.本文以建筑工程中常见的大型复杂桁架结构为例，通过分析VFIFE前处理模型数据结构，在云计算环境下实现程序计算过程的并行分布式处理，并与传统有限元处理方式[7-8]的结果进行对比.

2　并行计算节点分配模型

2.1节点标识规则及节点任务分配

2.1.1相关定义

在VFIFE分析中，空间几何实体经离散化处理，成为有限元模型[9]，然后按一定的规则将所有杆件和节点标识赋予唯一的编号值，通过节点的运动状态(位置、速度、加速度)来描述结构的运动状态[10]，并基于此进行分析和计算.尽管标识的顺序原则上不影响计算结果，可以是任意的，但节点标识的顺序对并行计算节点分配起着决定性的作用.

节点编号值排序的大部分方法是将问题转化为有限元网格所生成的各种图的顶点排序问题[11].传统有限元进行节点标识排序是为了保证有限元整体刚度矩阵的带宽最小，向量式有限元虽然无需集成刚度矩阵，但为了方便并行计算前对整体结构的划分，应该参照传统有限元的节点标识方式.

本文针对复杂桁架结构分析提出的节点标识方式参考了姜涛等[12]提出的优化算法.相关定义如下：

定义1相邻节点、节点的度与节点熵

在桁架结构中，由若干杆件围成的封闭图形称为一个单元r，在同一单元r内的所有节点互称为相邻节点.

假设任一节点u的所有相邻节点总数为d个，称为节点u的度，则节点u的相邻节点集合表示为Su={s1,s2,s3,…,sd}.

节点u所在的单元均称为该节点的相关单元，假设节点u的所有相关单元总数为j个，则节点u的相关单元集合表示为Ru={r1,r2,r3,…,rj}，该节点u的节点熵δ=d/j.

定义2桁架结构层次展开树

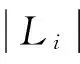
定义3直径端点

假设在定义2的桁架结构层次展开树LP中，其首结点为P，尾节点为Q，可使展开树树宽wp最小，则称P和Q为该结构的直径端点.

定义4合成展开树

假设构造以直径端点P和Q为根的桁架结构层次展开树LP={LP1,LP2,LP3,…,LPG}以及LQ={LQ1,LQ2,LQ3,…,LQF}，然后按照姜涛等[12]提出的算法合并树LP和LQ形成新的合成展开树L={D1,D2,D3,…,Dk}[13]，记树LP和LQ的宽度分别为wp和wq，则合成展开树L的树宽满足条件w≤min{wp,wq}.

定义5模型文件节点数据集

以桁架结构为例，前处理模型文件中，将节点信息表示为数据集node(N,T,ρ,M)，简称为节点数据集，其构成元素含义为：N={n0,n1,n2,…,nn}表示节点的编号值集合，集合中的ni表示每个节点的编号值(Id)，是由0至n的整型数据；T={a0,a1,a2,…,an}表示节点的类型集合，集合中的元素ai表示每个节点的类型，ai=0表示该节点类型为自由点，即无约束的点，ai=1表示该节点的约束类型为铰接，ai=2表示该节点的约束类型为刚接；ρ={ρnx,ρny,ρnz}表示节点坐标信息集合，其中ρn={ρn0,ρn1,ρn2,…,ρnn}，集合中的ρni表示每个节点的三维空间坐标值；M={m0,m1,m2,…,mn}表示节点的质量集合，集合中的mi表示每个节点的质量.

定义6模型文件杆件数据集

以桁架结构为例，前处理模型文件中，杆件信息表示为数据集element(E,NA,NB,C)，其构成元素含义为：E={e0,e1,e2,…,eH}表示杆件的编号值集合，集合中的ei表示每个杆件的编号值；NA={An0,An1,An2,…,AnH}，集合中的元素Ani表示每个杆件某一端的节点编号值，显然Ani∈N；NB={Bn0,Bn1,Bn2,…,BnH}中的元素Bni表示杆件另一端的节点编号值，同理有Bni∈N；数据集中的C表示该杆件的一些力学常数，包括杨氏模量、杆件的截面积及密度，以及杆件的极限应力，这些力学常量均为程式计算过程中所需参数.将杆件数据集element中的任一行表示为le(e,Na,Nb,C)，即编号为e的杆件.

2.1.2节点标识及分配规则

假设在任一桁架结构模型文件中，首先依据定义3选取模型文件节点数据集中距离最远的2个点P和Q作为直径端点，然后以这2个端点作为首节点生成该桁架结构的层次展开树LP和LQ.依据定义4合并为合成展开树L.对于合成展开树L={D1,D2,D3,…,Dk}，标识连续的正整数给D1上的节点，用最小编号值0标识展开树的起点P，设μ为D1中已标识节点中最小的，则按照节点熵δ增加的顺序对μ的相邻节点进行标识.迭代上一步骤完成本层大部分节点标识，对于本层的剩余节点，选择最小的节点编号值重复迭代过程，直到本层所有节点都被标识.从根节点层到最后一层依次重复上述算法，完成整体桁架结构的节点标识.

对于杆件的标识，同样依照节点编号值顺序来进行编号，从编号值最小的节点P开始，在其相邻节点中查找节点编号值最小的点，将最小编号0分给连接这2个点的杆件，然后再按照节点编号值增加的顺序分配连续正整数到以节点Q为端点的杆件.依次对其他节点进行上述过程，若遇到已经被标识的杆件则保留原编号，继续查找其他相邻点，直到结构中所有杆件均被标识.

在不考虑断裂的情况下，杆件与节点的拓扑数据，即模型文件中的杆件数据集element不会随时间变化发生改变，因而在并行计算前，只需对桁架结构的节点数据集node进行分配即可.结合以上特点，针对并行计算过程中节点分配模型，提出以下定义：

定义7基准节点与分区

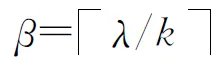
定义8分割杆件与分割节点

在程序计算的位移迭代公式中，是以各个节点为单位，迭代计算出节点在每一帧的位置，迭代公式(1)中，除了节点合力Fn中的节点内力fn需要根据当前帧的杆件长度计算外，其他数据均来源于定义5中的节点数据集node.而计算某一节点的内力fn需要先计算所有与该节点相连的杆件的长度变化，即需要杆件另一端节点的位置信息.在并行计算过程对输入数据进行划分时，应保证各个分区的整体性，即各个分区中的节点是连续的，而相邻的分区通过若干杆件相连，这种杆件定义为分割杆件，显然分割杆件的数量越少，并行计算时需要在各个分区外获取的数据量越小.分割杆件两端的节点均称为分割节点.

在上述节点重新标识的基础上，依据定义7和8，得出节点分配应遵循的原则：为了保证并行计算时负载的均衡，需尽量保证各个分区中分配到的子节点数据集大小相近.为了使程式计算的迭代过程顺利进行，需标记出各个分区中包含在分割杆件中的点，这些点需要随着每一次迭代而更新，并运用于2个或以上的分区.

2.2节点分配模型

根据第2.1节中的相关定义，本节给出具体的节点分配模型.

假设有一个桁架结构模型文件θ需要分配到k个分区中参与并行计算，基于定义5中的节点数据集node及定义6中的杆件数据集element，模型数据文件的构成可以表示为θ(F,node,element)，其中F(IdF,W,T)为模型数据文件中的外力元素，此集合中的元素IdF表示此外力的编号值，是由0至n的整型数据.元素W表示集中外力作用的3个要素信息，即力的大小、力的作用点及力的方向.集合中元素T表示力的斜坡加载时间参数，包括斜坡加载的开始时间、结束时间等，T的大小直接关系到程式计算生成的后处理行为数据文件大小.

基于以上分析，节点分配模型逻辑如下：

步骤1应依据定义4的合成展开树以及标识规则对模型的节点以及杆件进行重新标识，得到重新标识后的节点数据集node与杆件数据集element.

步骤2计算出节点数据集node的k个基准节点，依据定义7对基准节点的定义，得到基准节点的集合B{b1,b2,b3,…,bk}.

步骤5依据迭代式(1)，在程序计算过程中，外力元素数据集F只随迭代次数而发生变化，而杆件数据集element仅表示模型中杆件与节点的拓扑关系.故数据集F以及element不会依据每一次迭代的结果而更新数据，无需参与分块过程，仅需对节点数据集node进行分块.并行计算过程中，各计算节点共享数据集F与element.

步骤6在计算过程中需要将分割节点数据集nodeξ(N,T,ρ,M,ξ)储存在共享缓存中，依据分割节点的分区编号值对ξ(τ,ω)来选择计算时需要获取数据所在的分区，并随计算过程的每一次迭代而更新当前帧的数据.

3　分配模型算法及并行处理验证

根据第2.2节中节点分配模型的逻辑，本节将在Spark这一云计算平台下实现VFIFE复杂桁架结构程序计算的并行化，并使用资源管理器YARN进行任务的调度.Spark的编程模型与Hadoop的MapReduce编程模型非常类似，但是Spark中的容错并行数据结构(RDD)模型使得Spark可以实现数据集的相互转化和缓存等操作，这在处理迭代计算方面具有非常大的优势，因而成为本实验的首选.

3.1分配模型算法

并行处理以桁架结构的模型数据文件θ(F,node,element)为对象，其存储方式为多维数组，每一个数组元素表示一个外力元素信息或是节点、杆件的位置信息.首先对模型文件中的节点数据集node(N,T,ρ,M)按照本文的节点标识规则进行重新标识，在重新标识后即依据需要分成的分区数对节点进行分块，并将每个分区中的分割节点信息保存到RDD中，在每一次迭代完成后，需将上一帧中的节点信息同步到各个分区中，进行下一步迭代计算.

在Spark的编程模型中，核心计算部分引入了RDD的基于内存的MapReduce，底层依赖于Hadoop分布式文件系统(HDFS)和YARN/Mesos，因而本文中程序计算的并行分布式处理大致划分为2个阶段执行：Map和Reduce.Spark提供了一种共享变量——广播变量，可供所有机器获取其中数据，利用这个机制可以在所有Slave节点上共享只读数据.结合第2.2节的分析，本实验将输入文件中的数据集放入到广播变量中，以供所有Slave节点读取.

Spark的RDD可提供2种操作，即转换以及动作.转换可从RDD生成新的RDD，动作则能够将RDD数据集的执行结果写入存储系统或者传回驱动程序.在本实验的各个分区中，将并行地执行程序计算中的位移迭代公式，对各个分区中的模型文件节点数据集进行计算，而在计算当前帧时，会将当前帧和上一帧的节点位置信息保存到RDD中，并且对各帧的RDD进行缓存，以便下一步迭代的执行，同时还要写到输出的行为数据中作为记录.缓存的RDD一般存储在内存中，如果内存不够，可以写到磁盘上[14].

综上所述，基于Spark的向量式有限元复杂桁架结构并行分布式计算流程大致如图2所示.

图2　并行计算的流程图

结合上图，向量式有限元并行处理的步骤如下：

Driver：基于Spark的底层驱动类，可通过方法函数setMapper()、setCombiner()和setReducer()驱动Mapper类、Combiner类和Reducer类，从而在相应的类中实现Map、Combine以及ReduceByKey等操作函数对数据集进行处理.

Combiner：将节点上的Mapper输出进行规约操作，输出的对通过网络送到Reducer阶段，这里的Key与Mapper输出的Key相同，即各个节点的编号值N，Value为本次迭代得到的新一轮子节点数据集.

Reducer：这个过程执行的操作跟Combiner类似，将Combiner输出的具有相同Key值的Value进行整合，得到最终的结果，并以键值对的形式输出，这里的键值对格式为：Key<节点坐标>、Value<新的节点数据集>，即依据节点的编号值次序生成节点信息文件，输出的文件可直接用于后处理模块.输出的格式应参照后处理阶段的文件格式.

由于本并行算法是在对模型文件的节点数据集进行分块的基础上实现的，各个块的程式计算理论仍与串行计算一致，因而时间复杂度为O(n)，空间复杂度亦为O(n).

分配算法将集成到整个并行处理系统中进行验证.依据第1.2.1节的示例，后处理行为数据是程序计算输出的结果也是以数组形式存储的，每一帧的数据结构与模型文件数据结构类似.通过比较行为数据文件来验证算法的准确性.

3.2算法验证环境及数据准备

本文的Spark集群实验平台由3台普通PC机搭建，选择其中性能较高的1台PC作为主节点(Master)，运行Master节点守护进程，用于管理其他数据节点，其余2台作为从节点(Slave)，运行Slave节点守护进程，作为MapReduce任务运行的工作节点.所有主机处于同一局域网中，在配置局域网IP后，Master与Slave节点之间通过安全外壳协议(SSH)方式验证.程序计算代码由python实现，而且Spark平台有针对python的接口，即pyspark，因而本实验采用Spark on YARN的运行方式.

通过选取不同大小的模型文件进行节点标识及分配，并采用不同的分区个数，同时考虑划分的分区个数对实验结果的影响.

本文通过4个空间桁架系统计算模型来验证并行算法的有效性和加速效果.前2个模型model1与model2采用桁架节点数目较小的结构，后2个模型model3与model4则参照具体的工程实例，分别为钢结构桁架桥梁与单层钢结构厂房.

其中钢结构桁架桥梁的一些基本工程参数如表1所示.

表1　钢结构桁架桥梁结构参数

钢结构厂房的基本参数如表2所示.

表2　钢结构厂房结构参数

在创建以上2个工程实例模型时，外力作用均模拟横向风荷载.在本实验中，将桁架结构模型的复杂程度按照模型中的节点数目以及杆件数目作为依据进行分级，其中model1、model2、model3以及model4的节点数目和杆件数目分别如表3所示.

表3　测试模型信息

综上所述，实验中用于测试的桁架结构模型按照复杂程度由低到高依次为model1，model2，model3以及model4，在验证环节将通过对不同复杂程度的数据实验结果的对比，得出桁架结构模型复杂程度与VFIFE串行计算和并行计算效率的关系，从而归纳出VFIFE复杂桁架结构并行分布式处理技术的适用范围.

3.3验证过程及结果分析

VFIFE复杂桁架结构并行分布式处理实验包括并行计算实验与对照实验两大部分.并行计算实验的目的是通过控制Spark计算平台的分区数目来控制数据集的分区数目，从而研究分区数目与模型复杂程度的关系，寻找出各个模型的最佳分区数目.将最佳分区数目作为依据，与串行计算效率和传统有限元分析效率进行对比.根据第3.2节所描述的4种不同复杂程度的桁架结构模型以及实验环境限制，将并行计算实验的分区数目划分为4、8、12这3种.

对照实验的验证过程针对上一节中不同复杂程度的桁架结构模型进行，可分为横向对照与纵向对照，横向对照即对照不同复杂程度的桁架结构模型在相同条件下的计算结果，目的是研究模型复杂程度对实验结果的影响.纵向对照则针对各个模型比较，纵向对照实验主要是桁架结构VFIFE并行分布式处理与VFIFE程序串行计算效率的对照，将根据程序计算的迭代次数进行分类，进一步探寻桁架结构VFIFE程序计算中迭代次数与并行分布式处理效率的关系.

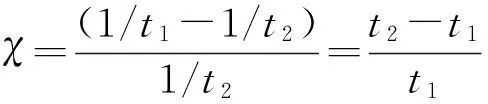
在对照实验中，向量式有限元的串行和并行等不同计算方式的计算效率则通过比较加速比ζ=t3/t4来分析，其中t3为串行计算时程序执行时间，t4则为相同任务量的前提下，采用并行计算算法时程序执行时间.

在所有上述实验中，最后都会将生成的行为数据输入到后处理模块中进行展示，得到更直观的结果.

对于第3.2节中创建的4个不同复杂程度的桁架结构模型进行并行计算，迭代次数设定为10 000次，将实验结果统计并整理后得到图3.

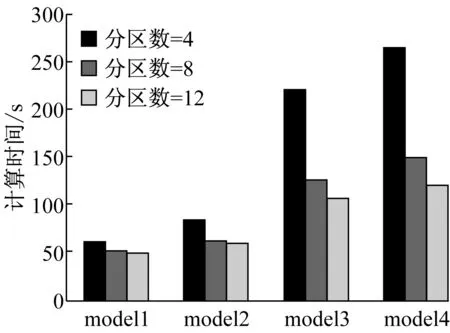
图3　不同桁架结构模型在不同分区数目下的计算时间

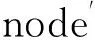
根据上述分析，由于硬件环境限制，本文的集群能运行的最大分区约为12，当继续增加分区数量时只会增加排队等待时间的开销，而不能继续大幅度提升计算效率.因此，可以选取分区数=8作为计算各个模型的分区数目来进行对照实验.

图4为对照实验中，不同模型在不同迭代次数下并行计算相对串行计算的加速比.

图4　　　　不同规模桁架模型在不同迭代次数下并行相对串行的计算加速比

Fig.4Speedup of parallel computing compared to serial computing dealing with different scales of models in different iterations

对比以上结果，分析VFIFE复杂桁架结构并行分布式处理相对串行计算的加速比，可以得到以下结论：

(1) 相对于串行计算，随着计算规模的增加，即桁架结构模型复杂程度的增加，并行计算能发挥出更好的性能.

(2) 在同一个复杂模型中，进行的迭代次数越多，并行计算的加速效果也更明显.这种加速效果在model1和model2中并不明显，但对于复杂程度较高的模型model3和model4，数据分块后并行计算带来的效益越高.

(3) model1以及model2的数据量相对较小，并行计算耗时略多于串行计算耗时，这可能是由于时间消耗在每一次迭代开始前，各个分区中的分割杆件两端节点需依据RDD中的数据同步.但总的来说，随着计算量的增加，并行计算的效率也越来越高，且与并行计算时分配的计算分区数目成一定正比关系.

4　结论与展望

(1) 本文针对节点数据集node采用的节点分配机制不会对计算结果产生影响，因为分配后的每个分区仍采用相同的计算流程.

(2) 对于数据量较大的桁架结构模型的计算，如节点数超过1 000，采用并行计算可使计算效率实现大幅提升.

(3) 在计算量较大的情况下，并行计算的效率与节点分配划分成的分区个数成一定正比关系，即分区的块越多，计算效率的提升越明显.

此后的研究应考虑划分更多块进行计算，找到最佳分块个数.完善程式计算理论，实现并行算法的通用性.

参考文献:

[1]Ting E C, Shih C, Wang Y K. Fundamentals of a vector form intrinsic finite element. Part I: basic procedure and a plane frame Element[J]. Journal of Mechanics, 2004, 20(2):113.

[2]Ting E C, Shih C, Wang Y K. Fundamentals of a vector form intrinsic finite element. Part Ⅱ: plane solid elements[J]. Journal of Mechanics, 2004, 20(2):123.

[3]Ting E C, Shih C, Wang Y K. Fundamentals of a vector form intrinsic finite element. Part Ⅲ: convected material frame and examples[J]. Journal of Mechanics, 2004, 20(2):133.

[4]卢哲刚，姚谏.向量式有限元：一种新型的数值方法[J].空间结构, 2012,18(1): 85.

LU Zhegang, YAO Jian. Vector form intrinsic finite element:a new numerical method [J]. Spatial Structures, 2012, 18(1): 85.

[5]杜庆峰，周晓玮，谢涛，等. 大规模向量式有限元行为数据压缩模型及算法[J]. 同济大学学报：自然科学版，2014, 42(11): 14.

DU Qingfeng, ZHOU Xiaowei, XIE Tao,etal. Massive vector form intrinsic finite element behavior data compression model and algorithm[J]. Journal of Tongji University: Natural Science, 2014, 42(11): 14.

[6]杜庆峰，周雪非，谢涛，等. 大规模向量式有限元行为数据无损压缩模型[J]. 同济大学学报：自然科学版，2015, 43(1): 19.

DU Qingfeng, ZHOU Xuefei, XIE Tao,etal. Massive vector form intrinsic finite element behavior data lossless compression model[J]. Journal of Tongji University: Natural Science, 2015, 43(1): 19.

[7]刘耀儒，周维垣，杨强. 三维有限元并行EBE方法[J].工程力学，2006，23(3): 27.

LIU Yaoru, ZHOU Weiyuan, YANG Qiang. Parallel 3D finite element analysis based on EBE method[J]. Engineering Mechanics,2006, 23(3): 27.

[8]符伟. 云计算环境下的线性有限元方法研究[D]. 武汉：华中科技大学, 2013.

FU Wei. Study on linear finite element method in cloud computing[D]. Wuhan: Huazhong University of Science and Technology, 2013.

[9]江雄心, 万平荣. 三维有限元网格节点编号优化[J]. 工程图学学报, 2008, 29(4): 22.

JIANG Xiongxin, WAN Pingrong. Optimization of node numbering in 3D finite element[J]. Journal of Engineering Graphics, 2008,29(4):22.

[10]倪秋斌，丁从潮，高博青，等.基于向量式结构力学的空间桁架非线性静力分析[J].空间结构, 2013, 19(3): 33.

NI Qiubin, DING Congchao, GAO Boqing,etal. Nonlinear static analysis of space truss using vector mechanics of structure[J]. Spatial Structures, 2013, 19(3): 33.

[11]荆国强, 陈德伟. 一种基于代数图论的有限元模型节点排序方法[J]. 同济大学学报：自然科学版, 2010, 38(6): 929.

JING Guoqiang, CHEN Dewei. A finite element nodal ordering with algebraic graph theory[J]. Journal of Tongji University: Natural Science, 2010, 38(6): 929.

[12]姜涛, 王安麟, 朱灯林. 有限元结点编号的综合带宽优化算法[J]. 机械设计, 2005, 22(11): 3.

JIANG Tao, WANG Anlin, ZHU Denglin. Synthetic bandwidth optimization algorithm of finite element node numbering[J]. Journal of Machine Design,2005, 22(11): 3.

[13]贾建军, 彭颖红. 三种基于图论的有限元结点编号优化算法[J]. 机械科学与技术, 1998, 17(5): 725.

JIA Jianjun, PENG Yinghong. Three graph theory based algorithms on FEM node ordering optimization[J]. Mechanical Science & Technology, 1998, 17(5): 725.

[14]梁彦. 基于分布式平台Spark和YARN的数据挖掘算法的并行化研究[D]. 中山：中山大学, 2014.

LIANG Yan. Research on parallelization of data mining algorithm based on distributed platform Spark and YARN[D]. Zhongshan: Zhongshan University, 2014.

收稿日期：2015-09-27

基金项目：国家自然科学基金(41171303)

中图分类号：TN919

文献标志码：A

Node Distributing Technology for Parallel Computing of Spatial Truss Structure Using Vector Form Intrinsic Finite Element

DU Qingfeng, WU Han

(School of Software Engineering, Tongji University, Shanghai 201804, China)

Abstract：After studying the computation rules in vector form intrinsic finite element(VFIFE) and the feature of spatial truss structure, a node distributing mechanism for parallel computing was proposed. According to the defined rules of decomposing, the model data of spatial truss structure were dynamically decomposed. Based on the results of decomposition, the data sets of nodes were dynamically decomposed, and the parallel computing was accomplished in the specific frame. The numerical experiments indicate that, the node distributing mechanism greatly improves the speed of spatial truss structure analysis, in contrast with those based on serial computing or classical finite element method.

Key words：vector form intrinsic finite element(VFIFE); spatial truss structure; parallel computing

第一作者： 杜庆峰(1968—)，男，教授，博士生导师，工学博士，主要研究方向为软件测试、计算机相关学科交叉领域.

E-mail：du_cloud@tongji.edu.cn