分析材料参数对二维固/固声子晶体能带结构的影响
李正伟 周 珺
(兰州交通大学,甘肃 兰州 730070)
分析材料参数对二维固/固声子晶体能带结构的影响
李正伟周珺
(兰州交通大学,甘肃兰州730070)
应用平面波展开法(PWE)分析了材料参数对二维固/固声子晶体能带结构的影响,发现散射体的剪切模量和密度是影响声子晶体能带结构的主要因素,杨氏模量对声子晶体能带结构的影响极小。当散射体的剪切模量小于基体时,声子晶体出现了多条带隙;反之声子晶体的带隙在填充率较大时出现,且与基体的剪切模量差值越大,声子晶体的带隙越宽。当散射体的密度小于基体时,只有在填充率较大时出现带隙且极窄;反之,声子晶体出现了多条带隙。继而采用钨、铍、碳、硅四种材料设计二维声子晶体,计算结果与上述推论颇为吻合,这为设计声子晶体在选材方面提供了理论依据。
声子晶体;平面波展开法;能带结构
0 引言
声子晶体[1]的带隙特性具有非常重要的理论价值和实际应用价值,因而受到广泛关注。周晓敏等人[2]研究了固/固声子晶体的声聚焦现象;陈阿丽等人[3]结合实验研究了二维8重固-流型准周期声子晶体带隙特性;Yantchev等人[4]探讨了声表面波的横向耦合特性;Sigalas等人[5]在研究二维声子晶体中的能带结构时发现,相比于将高速材料散射体填充到低速材料基体中所形成的的声子晶体,将低速材料散射体填充到高速材料基体中所形成的声子晶体,更容易得到带隙,且密度比越大,越容易产生带隙。
声子晶体是通过调节其带隙来实现对声波调控的。影响声子晶体带隙的结构参数分为两类:构成声子晶体的材料参数和结构参数,其中的材料参数主要包括各组分的材料密度、杨氏模量、剪切模量、波速以及声阻抗等。
1 基础理论
1.1声子晶体的本征方程
理想声子晶体是指在某个方向上具有无限多周期而其他方向上均匀且无限大的声子晶体,其理论模型就是式(1)

在弹性波理论中也称为弹性波方程。理想二维声子晶体由轴向无限长的柱体周期性分布在基体中构成;通常将二维晶格平面取为xOy平面,轴向取为z方向。将式(1)化成两个方程,分别是z轴方向的质点位移分量方程和xOy平面内的质点位移矢量方程。
z轴方向的位移分量,一般称为z模式的标量方程,如式(2)。

平面内的位移矢量,一般称为模式的矢量方程,有

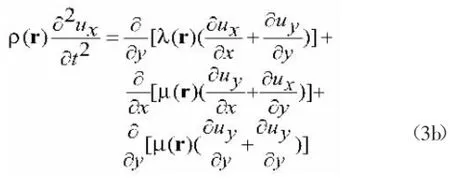
1.2平面波展开法
由于声子晶体具有周期性结构,可以把弹性常数、密度等参数按傅里叶级数展开,应用Bloch定理,将弹性波波动方程在倒格矢空间以平面波叠加的形式展开,即将波动方程转化为本征值求解,从而得到声子晶体的本征方程(4)和(5)。
Z模式的本征方程
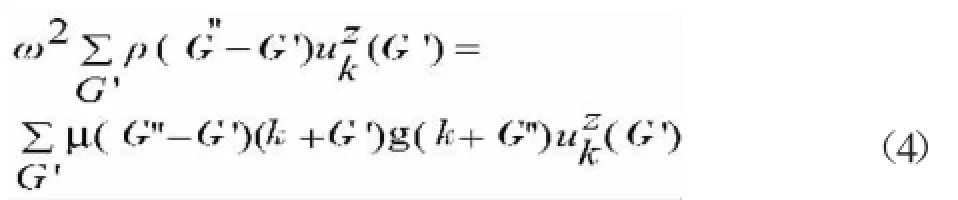
XY模式的本征方程

式(4)和式(5)为无限阶复数矩阵的特征值,其中G'取遍整个倒格矢空间。为了求得该问题的数值解,通常使用倒格矢空间原点附近的有限个倒格矢代替整个倒格矢空间,对称地进行近似求解。
2 材料参数对声子晶体能带结构的影响
(1)为便于分析材料参数对手二维固/固声子晶体带隙结构的影响,使材料的材料参数对声子晶体能带结构作用更为明显,假设构成声子晶体基体材料的相关参数见表1所示。

表1 基体参数
将散射体A以正方形排列的形式镶嵌在基体B中,形成二维声子晶体,见图1所示。

图1 二维声子晶体截面图
晶格常数a=0.02 m。设散射体的密度为3e3(kg·km-3)和杨氏模量为2e-3(1010Pa),在不同的剪切模量下所出现的带隙情况见表1所示。

表2 声子晶体能带结构
表2中剪切模量μ单位(1010Pa),散射体半径Rs单位(10-3m),频率ω单位为(kHz)。
表2中第一、二组数据显示:当散射体的剪切模量大于基体时,在填充率较大的地方出现声子晶体的带隙,且与基体的剪切模量差值较大,出现的带隙就越宽。比较第三、四组数据,发现在散射体的剪切模量小于基体时,即使在填充率很小,也会产生声子晶体带隙,声子晶体的能带并不会随着填充率的增加而无限增宽,而是会出现一个峰值,并出现了多层带隙。当散射体的剪切模量越是接近于基体时,产生的能带结构越宽,且能带条数越少。
同上,假设散射体满足如下条件:密度为3000kg·km-3和剪切模量为2e-3(1010Pa),在不同的杨氏模量情况下,所得到的声子晶体的能带结构见表3所示。

表3 二维声子晶体能带接结构
表中散射体半径Rs单位(10-3m)、频率ω单位(kHz)、杨氏模量E单位(1010Pa)
表3中的数据显示,在物质的密度和剪切模量非常接近的情况下,散射体的杨氏模量无论如何变化,都未出现声子晶体带隙。说明了材料的杨氏模量并不是影响声子晶体带隙的主要因素。
假设散射体的杨氏模量为2e-3(1010Pa),剪切模量为4e-3(1010Pa),在不同密度下产生的声子晶体能带结构见表4所示。

表4 声子晶体能带结构
表中散射体Rs的单位(10-3m)、密度单位(kg/m-3)、频率ω单位(kHz)。
表4中的数据表明,当散射体的密度小于基体密度时,声子晶体带隙会在填充率较大的情况下出现,且其带隙极为狭窄;当散射体的密度大于基体时,即使填充率很小,也会产生带隙,并且会出现多条带隙。
综上所述,剪切模量和密度是影响声子晶体能带结构的主要因素,而杨氏模量对声子晶体能带结构的影响极小。散射体的剪切模量比值与密度比值在远小于1时,声子晶体带隙在填充率较大时出现。散射体与基体的剪切模量比值在大于1时,声子晶体带隙在填充率较小时也会出现。
(2)声子晶体能带结构
选取钨、硅、碳、铍四种材料作为声子晶体的制作材料。它们的相关参数见表5所示。

表5 材料参数
比较这四种材料的相关参数,发现钨与碳的密度相差较大,而杨氏模量和剪切模量都比较接近。若用这两种材料设计声子晶体,若以碳为散射体,钨为基体,根据上述预测,该种声子晶体的带隙极窄,反之,若以碳为基体,钨为散射体,该种散射体具有多条能带。铍和硅的密度和杨氏模量相差很小,而剪切模量很大,若以铍为散射体,硅为基体。按上述条件设计的声子晶体的能带结构见表6所示。
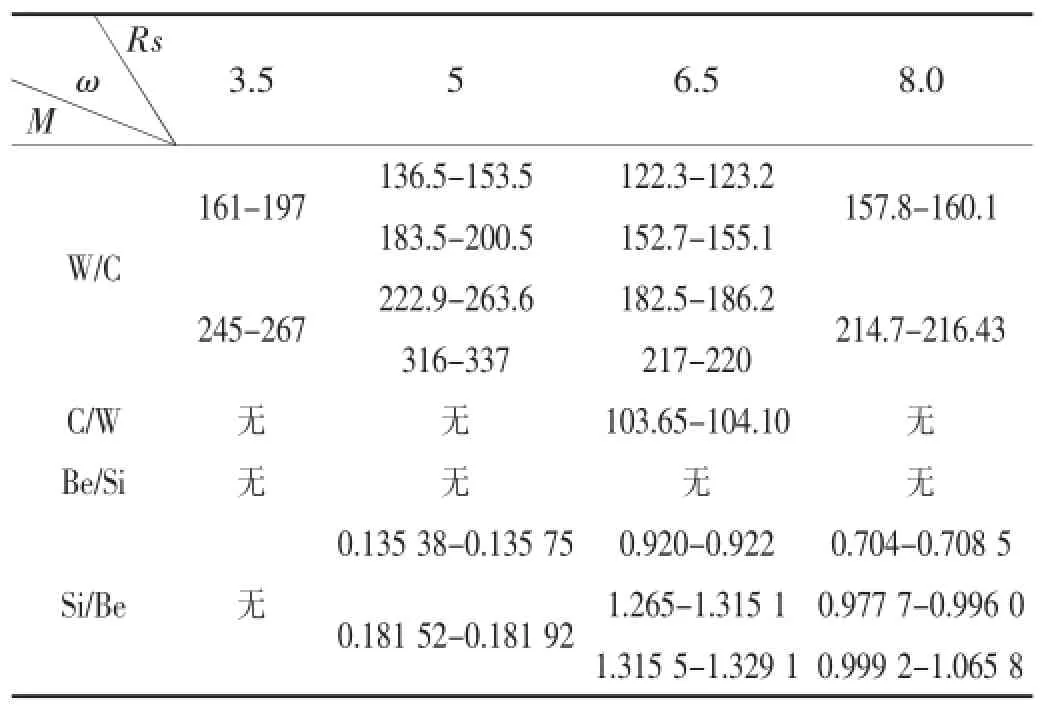
表6 声子晶体能带结构
表6中的数据说明在以钨为散射体而硅橡胶作为基体所设计的二维声子晶体在填充率很低的情况下就出现了声子晶体带隙,而将散射体与基体交换之后,仅在散射体半径Rs=0.006 5 m时出现了极窄的声子晶体带隙。而二维铍/硅声子晶体,无论填充率如何变化,都没有出现带隙,但二维硅/铍声子晶体则在整个填充率的变化过程中都会出现能带结构。这与前面分析所得结论颇为吻合。
3 结束语
在设计声子晶体时,通常应该将密度大的材料作为散射体,而将密度小的作为基体。在密度接近的情况下,将剪切模量较大的选作散射体,最后再考虑材料的杨氏模量。
[1] 温熙森,温激鸿,郁殿龙,等.声子晶体[M].北京:国防工业出版社,2009.
[2]Xiaoming Zhou,M.Badreddine Assouar.Acoustic super-focusing by solid phononic crystals[J].Applied physics letters 105.22355(2014).
[3] 陈阿丽,梁同丽,汪越胜.二维8重固-流型准周期声子晶体带隙特性研究[J].物理学报,2014,63(3).
[4] V.Yantchev.A transversely coupled phononic surface acoustic wave transducer[J].Applied Physics Letters 104(2014).
[5]M.Sigalas,N.Economou.Band structure of elastic waves in two dimensional Systems[J].Solid State Communications,1993 (86):141-143.
O735
A
10.3969/j.issn.1672-6375.2016.04.025
2016-2-18
李正伟(1987-),男,汉族,甘肃庆阳人,硕士研究生,主要从事声学材料的研究工作。

