基于个体公平原则的寿险产品定价模型
赵明清 张晓晓 陈玉澎

摘要在无套利框架的基础上,讨论基于个体公平原则下的寿险产品定价问题,即运用倒向随机微分方程理论,将投保人和保险人置于同一系统中进行考虑:首先,根据双方的随机投资决策目标分别建立无套利寿险定价模型和动态资产份额定价模型,得出两个特殊线性倒向随机微分方程的显式解;然后,建立基于个体公平原则的寿险定价模型,从投保人和保险人双方的角度对寿险产品进行公平定价,得出了从供需双方考虑的投资回报定价公式;最后,利用所建立的模型进行案例分析,计算出基于个体公平原则的保费及保险公司的投资策略.该寿险产品定价模型不仅考虑了保险人的意愿,还同时考虑了投保人的实际情况,因此,按此定价理念开发出的保险产品,不仅可以提高产品研发的成功率,而且使得研发出的新产品更能在竞争激烈的保险市场中站稳脚步.
关键词应用统计数学;寿险定价模型;无套利定价;资产份额定价;个体公平原则
中图分类号F840.32 文献标识码A
AbstractOn the basis of the no arbitrage pricing model, this article discussed the problem of life insurance product pricing based on the principle of individual equity. Using the theory of backward stochastic differential equation, the policyholders and the insured were considered in the same system. First of all, according to the target of the policy holder's investment decision, this paper established the non arbitrage life insurance pricing model ,and at the same time, according to the target of the insurer's investment decision, this paper established the asset share pricing model, and the explicit solutions of the two special linear backward stochastic differential equations were obtained. Then, this article established the life insurance pricing model based on the principle of individual equity. The model considers both the angle of the insured and the insurer, and obtains the pricing formula of the investment return. Finally, the insurance case was analyzed by using the established model, meanwhile, the insurance company's investment strategy and premium based on the principle of individual equity were calculated. The life insurance product pricing model considers both the insurer and the actual situation of the insured. Therefore, the insurance product developed by this pricing method can not only improve the success rate of product research and development, but also make the new products with stronger competitiveness in the fierce competition in the insurance market.
Key wordsApplied Statistical Mathematics;Life insurance pricing model;non arbitrage pricing;asset share pricing;individual equity principle
1引言
寿险定价是寿险产品开发的关键环节,准确合理的寿险定价对寿险公司的发展起着关键作用.随着保险业与金融业的关系越来越密切,寿险投资越来越普遍,因此考虑金融市场的投资情况,按照随机投资回报决策目标,建立动态的定价模型是非常有必要的.然而,从理论上讲,寿险产品可以看作是一种商品,寿险产品的价格应该由市场的供求关系决定,即由投保人和保险人共同决定,所以在无套利寿险定价理论的基础上,在同一系统中分别对投保人和保险人进行研究,考虑各自随机决策目标下的寿险定价模型,按此定价理念开发出的保险产品,不仅可以提高产品研发的成功率,而且使得研发出的新产品更能在竞争激烈的保险市场中站稳脚步.
目前,国内外对基于投资的寿险定价问题研究较少.Brennan、Schwartz(1976)最早将金融产品的定价方法应用到保险定价中,对保险产品进行合理定价[1];Trowbridge(1977)考虑了利率波动和通货膨胀对寿险定价的影响[2];Spellman(1975)等考虑了投资收入和需求弹性对寿险定价的影响,以利润最大化作为最终目标,建立寿险定价模型[3].Pardoux和彭实戈(1990)最早建立非线性下倒向随机微分方程的基本框架[4];石玉凤(2006)阐述了无套利寿险定价法及动态资产份额定价法,根据保险公司的决策目标,计算出合理保费及投资策略[5];郑鸬捷(2012)将无套利寿险定价运用到再保险定价中,加入时间序列预测方法,给出了基于投资的非比例再保险定价公式,为保险公司厘定比例再保险保费提供了新的方法[6].
在个人公平原则的基础上,从投保人和保险人双方的角度出发,把赔付情况与投资收益相结合,根据投保人和保险人各自的随机投资决策目标,分别建立基于倒向随机微分方程的无套利定价模型和动态资产份额定价模型,给出保费的定价公式(以上内容主要参考文献[1]),在此基础上增加寿险产品成功定价的个体公平条件,进而制定出更加合理的保费以及合理的投资策略.
2投保人无套利寿险定价模型
2.1模型构建的基本思想
投保人购买保险的行为可以看作是一种投资行为,初始时刻的投资金额是保费,到期时的预期投资回报是保险金额,因此对投保人来说并不是真正的参与到投资市场中进行投资,在投保人虚拟的投资过程中,只考虑投保人初始投资金额在投保期间的变动情况,不考虑投保人在投资期间的收入和消费等资产的变动情况.对投保人运用最基本的无套利定价模型,根据其预期投资回报目标,建立寿险定价模型,鉴于寿险定价的稳定性要求,投保人把保费投资于两种资产:即无风险资产和有风险资产.
2.2符号及模型假设
2.2.1符号
x岁的人投保的初始时刻记为0,投保时间长度记为T,无风险利率记为r0(一般认为是银行或国债的当期利率),有风险投资的预期收益率为μ,投资市场的随机波动系数为δ,t∈(0,T)时刻无风险资产的价格为p0(t),有风险资产的价格为pt,初始时刻需要缴纳的保费为P0,保费在t时刻的价值为Pt,T时刻的价值为PT=V即保额,保费中用于有风险投资的金额在t时刻的值为It.
2.2.2模型假设
(1)不考虑投保人在投保期间的收入、消费及投资交易成本;
(2)无风险投资定价过程满足:
由无套利定价公式可以看出,投保人预期的保险金额越高,则投保初期需要缴纳的保费就越高.
3保险人动态资产份额定价模型
3.1模型构建的基本思想
对于保险人来说,面对的是真实的投资环境,寿险产品的定价除了要考虑利率之外,还要考虑死亡率、退保率、各种费用率、保险金额等多种因素.在寿险定价方法中,动态资产份额定价法是一种能考虑多种因素并且得到广泛使用的定价方法之一,因此对于保险人可建立动态资产份额定价模型.保险人在保险期初的可投资金额除了收取的保费之外还可以利用公司期初的资产份额进行投资 ,考虑到寿险定价的稳健性,保险人将期初的资产份额和可投资保费投资于无风险和有风险两种资产,并且考虑到保险人的无风险投资相比投保人来说投资渠道更多,收益更具优越性,因此认为投保人的无风险投资收益率要比保险人的无风险收益率高,在保险期间资产份额经投资而不断增长,在保险期末达到预期的资产份额和必要的给付目标.
3.2符号及模型假设
3.2.1符号
记保单生效的初始时刻为0,保单的有效期为T,由于资产份额定价法注重短期定价的有效性,因此建立一年期的动态资产份额寿险定价模型,即T=1.设无风险投资回报率为r,有风险投资的预期收益率为μ,投资市场的随机波动系数为δ,t时刻无风险资产的价格为p0t,t时刻有风险资产的价格为pt,保险人年初拥有的资产份额为AS0,x岁的投保人在达到x+1岁之前的死亡率为q1x,投保人退保的概率为q2x,投保人生存并且不会退保的概率为p(τ)x,年末支付的退保金额为CV1,年末的死亡给付金额为B,初始时刻收取的保费为G0,与保费有关的费用比例为c0,与保单有关的费用为e0,t时刻动态资产份额的价值记为Ut,动态资产份额到T时刻的目标值为UT,其中用于有风险投资的金额在t时刻的值为It.
3.2.2模型假设
3.3模型建立
保险公司初始时刻可用于投资的资金包括两部分:一部分是扣除保单费用和保费费用后可用于投资的金额;另一部分是保险公司初始时刻的资产份额.即预期资产份额的增长有两部分构成:一部分是无风险投资收益,另一部分是有风险投资收益.
4基于个体公平原则的保险定价条件
寿险产品作为一种商品,必须对寿险产品进行合理的定价,因此在定价的过程中应该从投保人和保险人双方的角度出发,考虑个体公平原则,当投保人期望支付的保费大于或等于保险人期望收取的保费时,才能得到一个合理的保险定价,即在定价过程中需满足下面的定价条件
除此之外,在建立寿险定价模型的过程中,对有风险投资的回报率做出了假设,即有风险投资的回报率不低于无风险投资的回报率,也就意味着我们利用无套利寿险定价模型得出的保费含有有风险投资导致的因素,所以假如在期初将可投资资金全部投资于无风险资产,则得出的保费应该大于等于无套利寿险定价模型得出的保费.因对于投保人来说并不会真正的参与到投资市场中,只是一种虚拟的投资定价,所以只需要考虑保险人的保费定价满足无套利定价条件,即
5案例分析
保险公司新开发的一种面向X岁人的一年定期保险,保额为1000元,X岁的人在一年内死亡的概率为q1x=0.15,在一年内退保的概率为q2x=0.25,在一年内既不退保也未出险的概率为pτx=0.6,与保费有关的费用比例为c0=0.06,与保单有关的费用为e0=2,保单年末支付的退保金额为560元,保险公司第一年初拥有的资产份额为AS0=180,保险公司第一年末拥有的资产份额为AS1=500,投保人的无风险投资收益率为r0=0.0258,保险人的无风险投资收益率为r=0.035,计算保险公司第一年初需要收取的保费,同时计算保险公司的有风险投资额和无风险投资额.
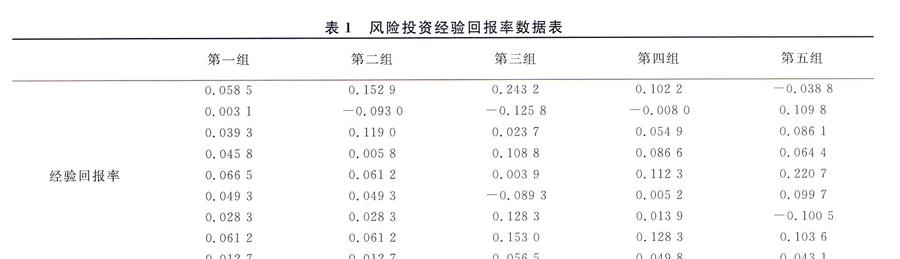
根据保险公司的有风险投资情况,引用文献[4]中的几组风险投资经验回报率的数据,见表1.
这个案例说明,保险人承保保额为1000元的保险,只需收取投保人387.737元的保费,同时将保险公司年初的资产和年初收取的保费进行投资,其中将226.27元投资于有风险资产,316.21元投资于无风险资产,一年后,保险公司就能够承担最高不超过1000元的赔付.
6结语
基于个体公平原则的无套利寿险定价为寿险产品的开发提供了一种新的思维方式,这不仅提高了寿险产品的成功率,也大大缩短了新产品的检验周期,通过合理的操作,帮助保险人获取更大的利润.在理论研究中,一般情况下我们只知道保险公司的期初资产份额,对保单期末的资产份额只能通过预测得到,利用基于个体公平原则的无套利寿险定价模型,可以根据决策目标,得出保单成功定价的期末资产份额所满足的条件,也即得出保险公司的利润空间,保险人在可获得的利润范围内对寿险产品进行定价,基于该原则下得出的保费更合理,开发出的新险种更容易适应日益激烈的保险市场.
参考文献
[1]Brennan M. J., Schwartz E. S. The pricing of equity-linked life insurance policies with an asset value guarantee[J].Journal of Financial Economies,1976,3(1):195-213.
[2]C. L. TROWBRIDGE. Adjustable life:a new solution to an old problem[J].CLU Journal,1977(40):202-206.
[3]Spellmam L. J., Witt R C, Rentz W. F. Investment income and nonlife insurance pricing[J].Journal of Risk and Insurance.1975(52):567-577.
[4]E. Pardoux, S. Peng. Adapted solution of backward stochastic differential equation[J]. Systems and Control Letters,1990(14):55-65.
[5]石玉凤.寿险产品优化理论模型与方法[M].北京:中国经济出版社,2006:162-214.
[6]郑鸬捷.基于投资的我国再保险预测性定价新探讨[J].经济数学,2012,29(3):94-99.
[7]龙卫洋,尤家香.基于投资回报的寿险供需定价决策模型的建立[J].管理世界,2013(3):174-175.
[8]刘海龙,吴冲锋.基于投资理论的保险定价公式[J].中国管理科学,2001,9(3):1-5.
[9]石玉凤,王立杰.动态资产份额定价理论模型[J].数学的实践与认识,2005,35(3):8-13.
[10]陈琳,柳向东,熊美莉.寿险模型在无套利框架下的定价分析[J].科学技术与工程,2010,10(31):7852-7855.
[11]彭实戈.倒向随机微分方程及其应用[J].数学进展,1997,26(2):98-111.
[12]柳向东,寇璐.带Poisson跳的无套利模型下的寿险定价分析[J].暨南大学学报,2012,33(5):339-443.

