互联网时代出租车供需匹配及补贴方案确定

刘嘉琪　邹泞憶　周梓楠　王颖喆

摘要通过建立出租车供求匹配的长期和短期模型给出了打车软件平台上优化的补贴方案.长期模型中，建立出租车需求量的多元线性回归模型和供应量公式.短期模型中，应用BP神经网络预测每天高、中、低峰的出租车需求量，建立高、中、低峰供应量多元线性自回归模型.以西安市为例，在模型的基础上，通过分析实时数据得出分时段的适用于网络平台的平衡供需的补贴方案.互联网时代的补贴方案依赖于实时更新，广泛全面的大数据，更及时，多样，具有针对性，不仅有效实现了软件平台公司的盈利，也最大可能地满足了乘客，政府，由司机代表的出租车公司的需求，充分发挥了互联网在优化出租车运营方式方面的作用.

关键词应用数学；出租车供需匹配；补贴方案；神经网络；多元回归

中图分类号O29，O213，F572文献标识码A

AbstractBy building long and short term models of matching degree of taxi supply and demand， an optimization of the subsidy scheme on a taxi software platform was determined. In the long term model， a multiple linear regression model of taxi demand and a formula measuring supply were given. In the short term model， BP Neural Network and the multiple regression model were used to measure taxi demand and supply respectively for high， medium and low peak. Taking Xi'an as an example， through the analysis of realtime data， a timedivision taxi optimization subsidy scheme on Internet platform was determined. Based on timely updated， extensive and comprehensive big data， subsidy schemes in the Internet age are more timely varied and specific. Making full use of the Internet in optimizing taxi operation mode， these schemes not only realize profit making of software platform companies， but also meet the needs of passengers， the government and taxi companies to the greatest extent.

Key wordsapplied mathematics； matching degree of taxi supply and demand； subsidy schemes； Neural Network； multiple regression model

1引言

近年来，作为城市客运交通的重要组成部分，出租车业发展迅速，但“打车难”问题也越来越突出.步入“互联网时代”，多家公司依托互联网建立打车软件服务平台，在使乘客与出租车司机之间信息互通的同时推出了比传统补贴方案更及时，更灵活，更有针对性的出租车补贴方案，以期实现出租车需求与供应的调整，获得更大盈利并解决“打车难”问题，因此在了解出租车供求匹配程度的基础上制定最优的补贴方案就具有重要的现实意义.

传统的对出租车行业的研究主要集中于对城市出租车需求和拥有量的预测.在预测出租车需求方面，以Douglas为代表的国外学者利用较为复杂的数学模型，Douglas（1972）提出出租车的需求是其平均出行费用和平均等候时间的减函数[1]，J.Enrique等运用经济学的方法，将出租车客运需求定义为价格的广义函数[2].国内学者提出了一些计算较简单的预测方法并应用于实例分析，黄仕进，杨海等在1999年的改进模型中建立非线性方程和神经网络的模型来表述需求并应用于香港出租车汽车市场[3] [4]，徐炜运用多元线性回归方法预测深圳市出租车运力投放[5]，卢毅使用神经网络BP算法仿真模拟[6].在预测出租车拥有量方面，陆建（2004）根据城市居民和流动人口出行特征[7]，李智宏使用供需平衡法[8]，车岚（2006）在大量数据的基础上应用统计回归方法[9].由于数据的限制，这些研究在一定情况下成功地预测了供应量和需求量，适合于较长时间较广范围内对供需状态大致趋势的预测，但不能及时为出租车运营提出有效的有针对的平衡供需措施.

步入互联网时代，学者又将目光转向了如何利用互联网平衡供需，优化出租车运营方式.李伟丽等（2015）[10]，刘佳倩等（2015）[11]分析了北京市不同经济分区和一天不同时段的出租车资源配置，研究的时空范围更加精确并提出了比较粗糙的平衡供需的补贴方案.戚蓓蓓等[12]，陈丽贞[13]等分析了打车软件上推出的补贴方案对平衡供需的作用.但同时，互联网时代的到来也对出租车行业发展提出了新的挑战，张朝霞（2015）[14]指出了原有的出租车行业管理体制在互联网时代的不足，肖沛然（2015）[15]指出互联网专车服务在打破出租车行业垄断的同时将促进整个行业的深层次改革.这些研究填补了传统供需平衡研究的空白，打车软件的出现使得实时数据的获取成为可能，据此可以得到具有高实效性的供需状态预测，进而对不同区域在不同时刻借助提出多样的补贴措施以平衡供需.但这些研究只分析了互联网和已有的补贴措施在平衡供需方面的效用，没有提出如何制定不同情况下的适用于网络平台的补贴方案，未能最大发挥互联网在优化出租车运营方式方面的作用.

建立长期和短期的供需平衡模型，以西安市为例，应用长期模型从总体上把握西安市出租车供需平衡状态，然后根据短期模型定量分析西安市出租车实时的供需状态，在此基础上，应用神经网络方法给出适用于打车软件平台上的随时更新的出租车优化“补贴”方案，希望能对出租车运营管理和城市交通管理提出有效的建议方案.

2出租车供需模型

2.1相关定义

根据数据特点，对应长期和短期供需关系模型，分别采用长期和短期两种方式定义需求量、供应量及供求匹配程度.长期定义以年为单位变化，主要体现宏观经济指标对供需平衡的影响，短期定义针对每一时刻，主要体现每时每刻交通状况对供需平衡的影响.

2.1.1长期定义

长期模型是通过城市宏观经济特征和居民出行特征来预测出租车供需状态，进而给出相应变量定义及单位.

需求量：每年出租车承担的出租车乘客人数和尚未被满足的潜在出租车乘客人数之和，单位“万人次”.

供应量：当年运营出租车可以承担的出租车乘客数量，单位“万人次”.

供求匹配程度：选择出租车供应量和需求量之比适应度M作为衡量较长时间内供求匹配程度的指标.T为出租车客运供应量（万人次），D为出租车客运需求量（万人次）[16]，则适应度为

M=DT.（1）

一般的，认为当1.25≤M≤1.40时，出租汽车客运需求与供应量基本达到平衡；当M < 1.25时，出租车供应量较小，不能很好地满足乘客需求；当M >1.40时，出租车供应量过大，超过需求，造成资源浪费.[17]

2.1.2短期定义

需求量：某时刻出租车订单量，包括已成功提交和未成功提交的.认为一辆出租车完成一份订单，因此确定需求量单位为“车次”.

供应量：某时刻运营出租车量，单位“车次”.

供求匹配程度：选择出租车需求量和供应量之比需供比γ作为衡量某一时刻供求匹配程度的指标.不同于出租车实载率，此处定义的γ包括了想打车但未打上车的乘客.

Q，T分别代表出租车需求量和供给量，需求量与供应量之比γ为

γ=QT.

供求匹配关系：当出租车供应量略大于需求量时，出租车资源流动顺畅，因此认为γ在65%～80%之间取值时，出租汽车客运需求与供给基本达到平衡.

2.2供需模型建立

以西安市为例，建立出租车供需匹配程度的长期和短期模型.长期模型旨在分析较长时间内（年）出租车资源的大致供求关系，在长期定义下，分别建立需求量和供应量计算模型，采用适应度作为供求匹配关系的衡量指标.短期模型旨在分析不同时刻出租车资源的供求匹配程度，将一天划分为四个时间板块，分别对应于居民出行量的高峰，中峰，高峰，低峰.在短期定义下，分别建立需求量和供应量计算模型，采用需供比作为供求匹配关系的衡量指标.

2.2.1长期模型

（1）需求量多元线性回归模型

首先选取与需求量有显著关系的空间影响因素.需求量影响因素分为经济因素，公共交通因素和社会因素三类.经济因素包括国内生产总值（GDP），人均可支配收入和居民消费水平，公共交通因素包括出租车客运量和公交车数量，社会因素包括常住人口数和社会从业人数.将出租车客运需求量分别与这些因素进行相关性分析，选择显著相关的影响因素.然后将出租车客运需求量作为因变量，显著影响因素作为自变量，建立多元回归线性模型如式（2）.

D=a0+∑aixi+ε.（2）

其中，D为出租车客运需求量，xi为需求量显著影响因素，ε为残差，ai为待定的回归系数.

（2）供应量计算模型

考虑到出租车供应量乘以载客率可大致反映出租车实际日均客运量[7]，供应量T由下列公式近似确定：

T=α1-ρ，（3）

其中，α为城市出租车日均客运量，ρ为出租车空载率.

2.2.2短期模型

（1）需求量人工神经网络模型

出租车需求量的影响因素很多，通过建立函数关系进行准确预测是不现实的.而人工神经网络能从数据样本中学习以前的经验并自动逼近那些最佳刻画了样本数据规律的函数，因此可以对城市公共交通需求进行较好的预测.

采用人工神经BP网络（Backpropagation NN），网络除输入输出节点外，还有一层或多层的隐层节点，同层节点中无耦合.输入信号从输入层节点，依次穿过各隐层节点，传到输出节点，每一层节点的输出只能影响下一层节点.进行人工神经网络预测时，首先确定输入、输出参数，输入层共三个输入信号，打车难易度d，订单平均被抢时间t，平均车费c，输出层为出租车真实需求量，选择隐含层节点数为2.然后，确定初始条件，将已有数据分为训练样本和检验样本.最后对输入、输出数据进行“归一化”，使得网络输入变量的值域为[0 ，1].根据已有的打车难易度，订单平均被抢时间，平均车费和出租车真实需求量数据，使用SPSS对数据进行训练，得到城市出租车需求量的神经网络模型估计值 [6] .

（2）供应量多元自回归模型

考虑高、中、低峰之间的互相影响和实时收入对出租车运营量的影响，建立三个方程的供应量多元线性模型.类似空间的需求量模型，供应量的影响因素也可分为经济因素，交通因素和社会因素.以天为时间单位，一些经济政治因素如GDP，人均收入水平等不会有明显变化，但是交通通畅状况，司机收入是供应量周期性变化的主要影响因素.交通通畅状况可以用人口出行量来刻画，体现在高、中、低峰之间的相互关系.从早上6点开始，将一天看作高—中—高—低峰的循环，建立多元回归模型时，高峰供应量是中、低峰供应量的影响因素，中、低峰供应量是高峰供应量的影响因素.可以用车费直接刻画出租车司机的收入.进行相关性检验后建立多元线性回归模型如下：

3实例分析

以西安市为例，使用SPSS软件分别建立西安市出租车供需匹配程度的长期和短期模型.长期模型采用《西安市统计年鉴》2000-2009年GDP，人均可支配收入，人均消费支出，公交车数量，常住人口，从业人口，出租车客运需求量数据，进行显著性检验之后，根据长期模型计算西安市出租车适应度，作为西安市供需匹配程度的长期总体刻画.短期模型采用滴滴快的智能出行平台“苍穹”上2015年9月6日-11日出租车分布，打车难易度，打车需求量，被抢单时间，车费的实时变化数据，根据短期模型得到西安市出租车高，中，低峰需供比，作为西安市实时供需匹配程度的刻画.

3.1长期模型

首先，使用SPSS进行GDP，城镇居民人均可支配收入，城镇居民人均消费支出，公交车数量，常住人口数，社会从业人口数和出租车客运量的相关性分析.在显著性水平0.01下，选择西安市GDP、人均可支配收入、人均消费量、公交车数量、常住人口数量和就业人口数量这些与出租车客运需求量高度正相关的空间影响因素作为自变量，西安市出租车客运需求量作为因变量，构建需求量多元线性回归模型.

供应量多元自回归模型中，2014年西安市出租车日均客运量α为120万人次，空载率ρ为50%，由公式（3）得西安市2014年出租车供应量

T=1200.5=240（万人次）.

根据公式（1）得西安市出租车资源适应度

M=QT=240169。718=1.41.

因此2014年西安市出租车客运适应度略偏离最佳范围，供求匹配不平衡.

可以看出，以西安为代表的西北内陆地区的出租车资源配置整体上“供过于求”，这与我国中西部地区人口密度较为稀疏、经济发展水平较为落后的实情有关，然而这种对资源配置的描述是粗糙的，只体现了出租车资源配置在较长时间内的平均状况.事实上，虽然一天的大部分时间内出租车客运供应量多于需求量，但在出租车行业获利的黄金时段“早高峰”和“晚高峰”，“打车难”仍然普遍存在，因此需要进一步建立短期模型得到出租车资源配置的实时定量刻画.

3.2短期模型

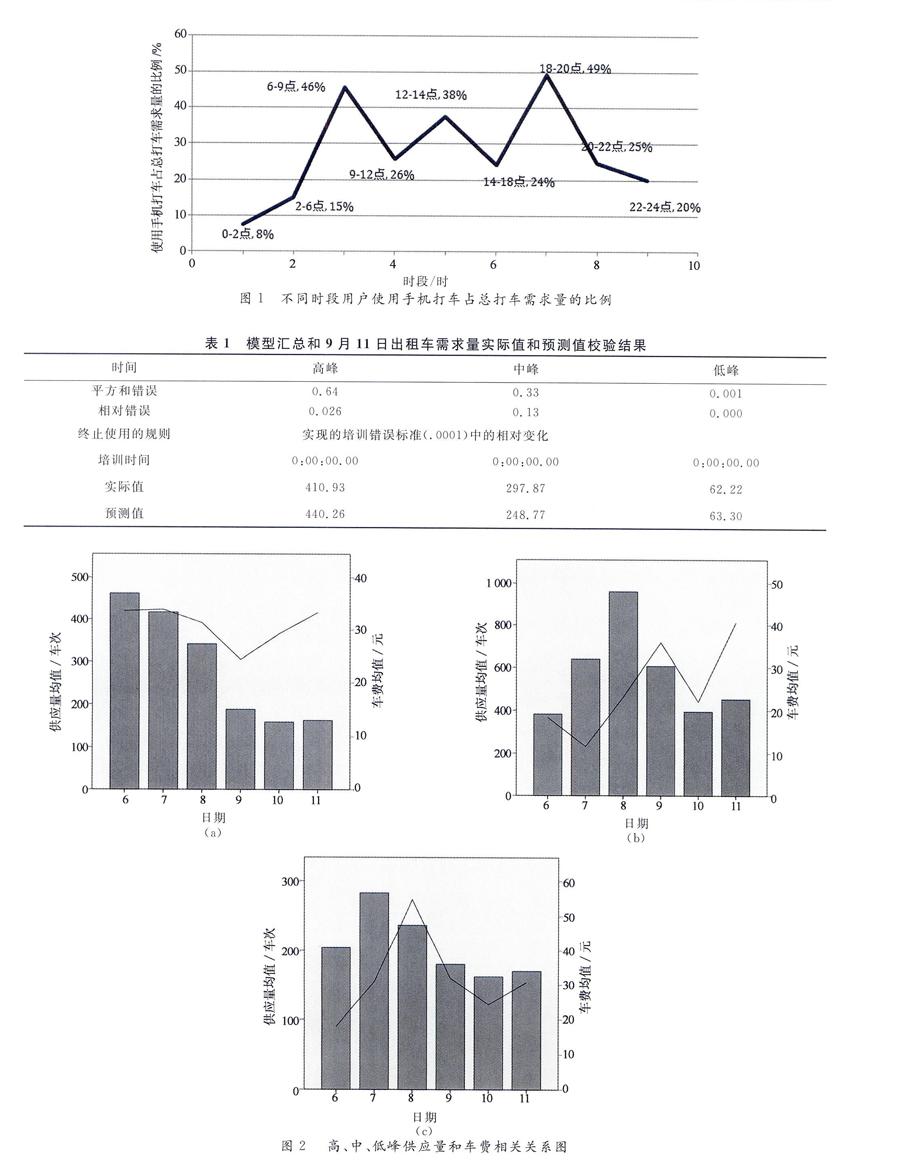
西安市以钟楼为中心的四条大街是交通动脉，东北，西北，西南，东南四块地区地区内部发展水平大致相当，构成高速发展的二环.采集数据时，以位于东南西北四条大街和东北，西北，西南，东南的八个点代表西安的整体交通状况.选择17∶00-19∶00的数据代表高峰交通状况，13∶00-15∶00的数据代表中峰，凌晨2∶00-4∶00的数据代表低峰.得到西安市2015年9月6-11日八个方位软件平台上，高中低峰出租车分布和打车难易度，打车需求量，被抢单时间，车费的实时变化数据，据此估算真实供应量.再根据图1，高，中，低峰时打车软件上的打车需求量分别占总需求量的49.4%，37.5%，15.0%，可以由“苍穹数据”估算出西安9月6-11日每日随时间变化的真实供应量.

需求量人工神经网络模型中，使用SPSS对数据进行训练，待网络训练稳定后，得到如下的模型汇总和9月11日出租车需求量实际值和预测值校验结果（见表1）.

供应量多元自回归模型中，先对选择出的供应量影响因素进行相关性检验.分别画出高、中、低峰西安9月6日-11日供应量与车费之间关系图可以看到车费和供应量的变化趋势近似相同，再使用SPSS进行相关性检验，得到在显著性水平小于0.01时，西安市出租车供应量和车费之间存在显著的相关关系，因此用车费对供应量的影响来体现实时收入对出租车运营量的影响是合理且可以接受的.

根据西安9月6日-11日的数据，通过Matlab拟合，得到参数的最小二乘估计即公式（4）.短期模型下，高、中、低峰出租车供应量多元线性回归模型结果如下：

T1=-395.1-0.095T2-0.44T3+28.92c1+ε1，

T2=2763.7-4.97T1+4.86c2+ε2，

T3=13415-25.37T1+82.65c3+ε3.

用SPSS分别对模型中T1、T2、T3进行显著性检验，得到显著性水平分别为0.445、0.929、0.147，均大于0.05，故接受原假设，即上述建立的多元回归模型是合理的.

4互联网时代的“补贴”方案确定

长期模型给出了西安市出租车资源配置的整体状况，短期模型定量刻画了西安市出租车供需的实时变化.和传统出租车运营方式相比，互联网时代实时数据的获得和公布成为可能，从而可以采用补贴的方式及时平衡供需.本节将给出利用打车软件上的出租车运营实时数据来制定可以公布在互联网平台上的实时补贴方案的方法，从而实现在低峰时段增加需求量减少供应量，在高峰时段增加供应量适当减少需求量，最大发挥互联网在优化出租车运营方式方面的作用.

4.1方案确定

以“快的”和“滴滴”两家较大出租车公司打车软件补贴方案为例，目前已实施过的补贴形式有三种：1.间接给乘客补贴，多采用向新用户提供购物券的方式；2.直接给乘客补贴，减少车费金额，多有订单数目封顶；3.直接给司机一定金额奖励，多有订单封顶.间接补贴方式收效甚微，不予考虑.扩展“补贴”的含义，认为给司机“补贴”为增加司机的每单收入，给乘客“补贴”包括减少和提高乘客的每单支出两方面，创造性的将后两种直接补贴方案结合起来，将一

天划分为高，中，低峰，应用BP神经网络得到为使供需匹配，即需供比

计算过程如下.以收集的西安市9月6日-11日的实时数据为训练样本，通过神经网络得到在不同补贴额下的供应量和需求量数据，从中挑选22组，其中20组作为训练样本，2组作为考核本系统的检验样本.取上述数据里高、中、低峰9月6日-11日打车难易度d，订单平均被抢时间t的平均值，为使出租车供需平衡，将出租车需求量与供应量之比

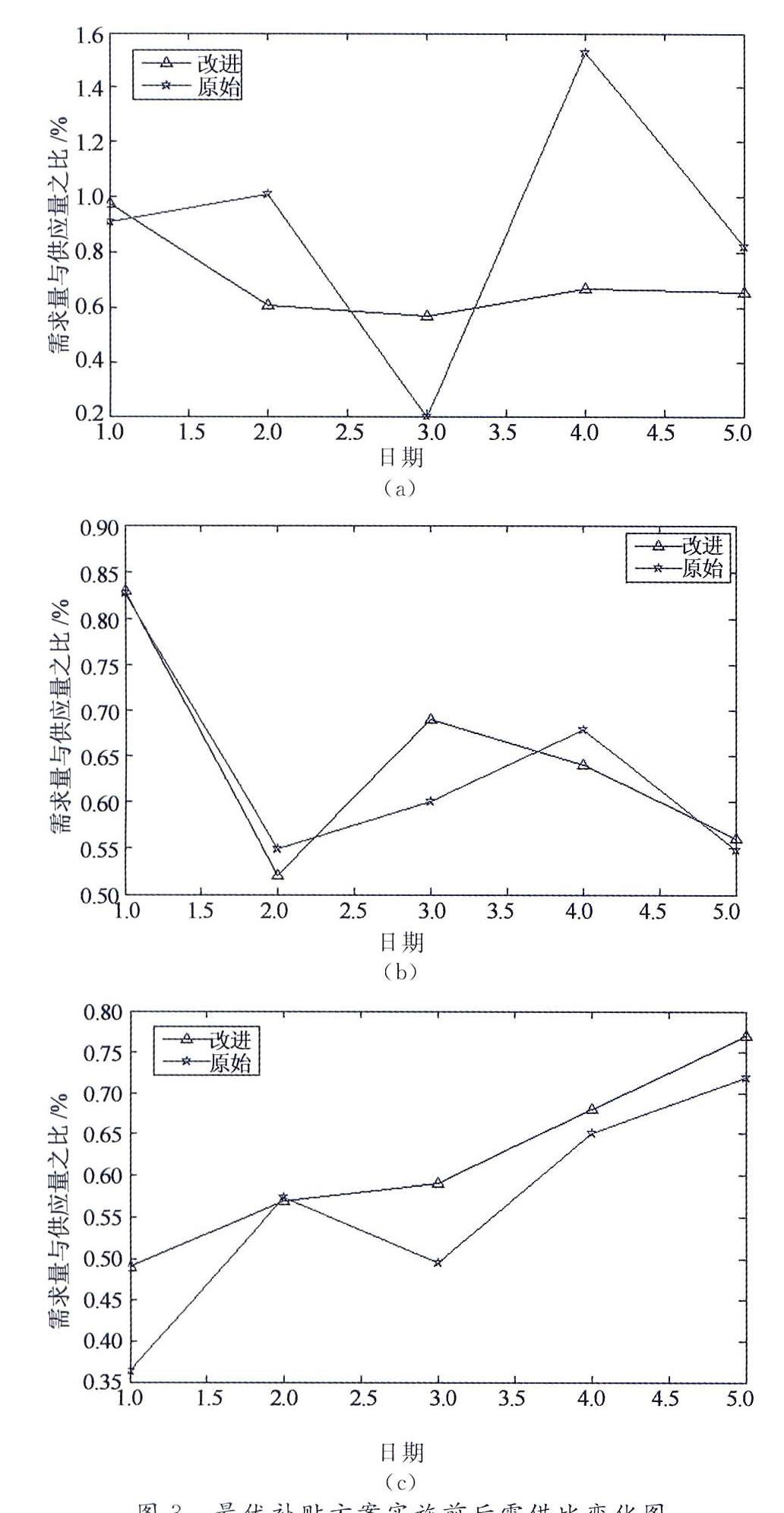
然后将上述补贴方案应用于西安市9月7日-11日的数据中，得到如表3补贴方案实施前后，需求量与供应量之比对比.补贴前的数据是根据苍穹数据和BP神经网络训练得到的需供比的真实值，补贴后的数据是在采取上述补贴方案之后，改变神经网络的“平均车费”参数得到的需供比的短期模型预测值.可以看到，补贴方案高峰的模拟结果最好，其次是低峰，总体而言，补贴政策使一天的出租车需求量与供应量之比更加接近70%，即接近供求平衡.

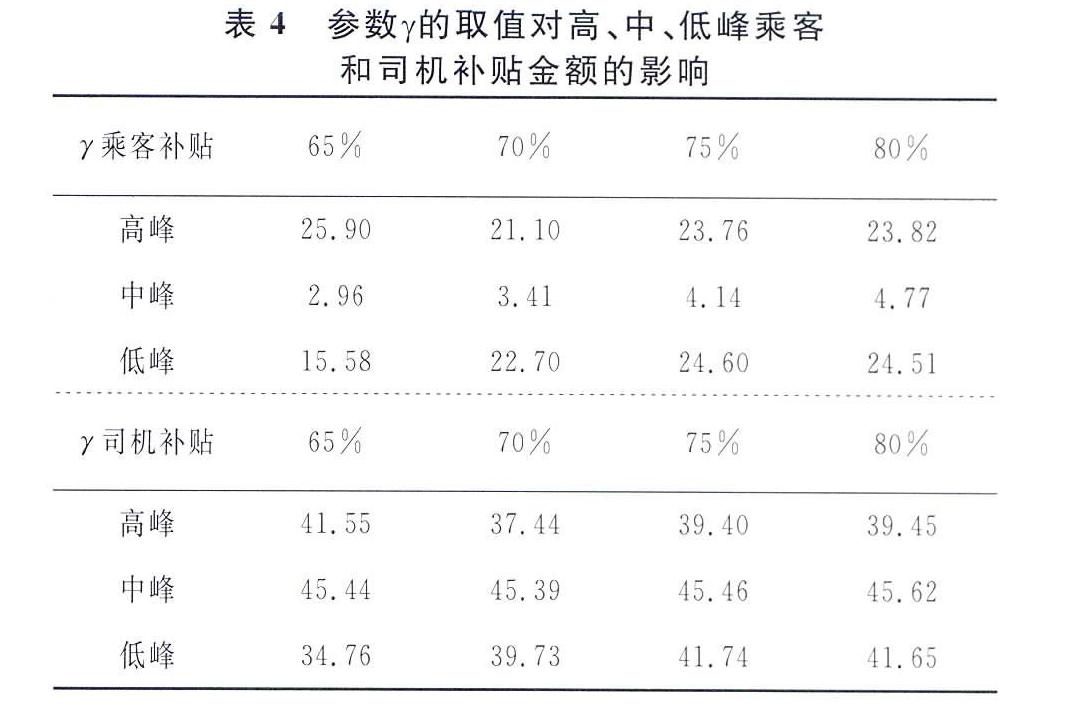
最后对参数γ进行灵敏度检验，分别令γ取值65%，70%，75%，80%，得到高，中，低峰乘客和司机补贴金额如表4，发现参数γ的取值对补贴金额的影响是不灵敏的即表3的补贴方案是适用的.

4.2方案评价与展望

和传统出租车补贴方案对比，互联网时代的补贴方案利用大数据，给出了更及时，更灵活，更有针对性的方案：[17]

（1）由于数据收集的局限，传统时代的补贴方案平衡的其实是几周前或几月前的出租车资源配置情况，而互联网平台上数据的实时性使得补贴方案的实时性成为可能，可以为出租车司机提供最新的信息指导.

（2）传统出租车补贴方案为每月支付固定的补贴金，而互联网时代的补贴方案考虑司机业绩，方式更加多样且快捷.

（3）软件平台实现了司机与乘客信息的实时互通，双向的资源调配更有针对性，对出租车司机可以大幅降低空驶率，增加收入，对乘客可以有效降低候车时间.

模型得到的补贴方案基于一辆车在一个时刻只能完成一单的假设，且主要优化目的为平衡供需，除此之外还可以有其他方式和其他因素主导的补贴方案：

（1）在司机和乘客同意的基础上，鼓励合理拼车

（2）对没有发生事故或违章的司机额外补贴

（3）根据行驶路况进行补贴，如对行驶边远市区进行额外补贴

（4）给出租车分发积分卡或好评返现

（5）根据使用打车软件次数给乘客进行补贴

5结论

以西安市为例，建立了长期和短期出租车供需关系模型，进而得出分时段出租车优化的“补贴”方案，为“滴滴快的”等出租车软件平台提供了一种实时补贴的思路和补贴金额的确定方法.根据实时的交通状况，可以在软件平台上及时发布给司机和乘客的“补贴”额，随时调整出租车资源的供需匹配程度.高峰段，需求量过高且为硬性需求，因此增加乘客车费进而给司机更高的补贴，使供应量增加，需求量适当减少，不仅使供需关系更加平衡，还增加了出租车公司和打车软件公司的收益.中峰段，道路状况良好，给乘客补贴使那些本没有打车计划的出行人口选择出租车方式，给司机补贴使更多的司机愿意出车为将要到来的高峰段做准备.低峰段，需求量明显减少，给乘客高的补贴使更多的出行人口选择出租车，给司机较高的补贴使司机愿意跑夜车，这样可以减少晚上或凌晨打车的乘客的候车时间.在这样的“补贴”政策下，充分发挥了互联网的作用，不仅实现了软件平台公司的盈利，也最大可能地满足了乘客，政府，由司机代表的出租车公司的需求，使得供需关系匹配程度得以提高.

参考文献

[1]G.W. Douglas. Price regulation and optimal service standards： The taxicab industry [J]. Journal of Transport Economics and Policy. 1972， 20（1）： 16-127.

[2]Daniel Flores-guri. An economic analysis of regulated taxicab market[J]. Review of Industrial Organization， 2003（93）： 594～615.

[3]H. Yang，S.C. Wong. A network equilibrium model of urban taxi services [J]. Transportation Research 32B，1998， 32（4）： 235-246.

[4]J.M. Xu， S.C. Wong， H. Yang， C.O. Tong. Modeling the level of urban taxi services using a neural network[J]. ASCE Jorunal of Transportation Enginerring 1999（ 125）：213-216.

[5]徐炜. 深圳市出租小汽车运力投放研究[D].吉林大学商学院，2005.

[6]卢毅， 王礼志， 卢旭. 城市出租车需求仿真预测模型研究[J]. 长沙交通学院学报， 2007（4）： 23-27.

[7]陆建，王炜.城市出租车拥有量确定方法[J]. 交通运输工程学报. 2004（3）：92-95.

[8]李智宏.成都市2005、2010年中心城区出租汽车发展规划调研报告[R].成都市出租汽车管理处，2002.

[9]车岚.城市出租车发展现状及需求预测[J].山西科技.2006（6）：89-91.

[10]李伟丽，杨鹏辉，孙漩，蒋文安. 互联网+时代下出租车资源配置研究[J]. 海南师范大学学报（自然科学版），2015，28（4）：367-374.

[11]刘佳倩，朱家明，李之好，李金玲. “互联网+”时代出租车供需匹配测度及补贴方案效应分析[J]. 上海工程技术大学学报，2015，29（4）：378-382.

[12]戚蓓蓓，朱家明，秦欢，从雨佳. “互联网+”时代的出租车资源配置[J]. 交通企业管理，2015，328（12）：44-47.

[13]陈丽贞，陈丽珊.“互联网+”时代出租车补贴效果实证研究[J]. 赤峰学院学报（自然科学版），2015，31（12）：109-111.

[14]张朝霞，秦青松，张勇. “互联网+”时代客运出租车管理改革方向探讨[J]. 价格理论与实践，2015，373（7）：17-20.

[15]肖沛然.互联网专车服务对出租车行业垄断的影响[J]. 经济数学，2015，32（4）：21-26.

[16]范合君，杜博.特大城市出租车合理数量估计及实现路径：以北京市为例[J]. 经济与研究管理，2015，36（8）：91-95.

[17]安晓丹，赵杰，章林枫，王济荣. “互联网+”时代的出租车资源配置[J]. 运城学院学报， 2015（6）： 34-37.