圆锥曲线焦点弦问题的解法探讨
马翔羽
(宁夏吴忠市回民中学 宁夏吴忠 751100)
圆锥曲线焦点弦问题的解法探讨
马翔羽
(宁夏吴忠市回民中学 宁夏吴忠 751100)
在求解圆锥曲线的焦点弦问题中,可以结合椭圆的几何定义,借助焦半径公式和代数方法进行求解,从一般问题延伸到特殊问题,将横向思考方法和纵向思考方法相结合,才能保证圆锥曲线焦点弦问题正确快速求决。
圆锥曲线;焦点弦;求解方法
在高中平面解析几何中,圆锥曲线的问题一直都是重点和难点,其中圆锥曲线的焦点弦问题涉及颇多,通常出现在解答题中,分值较重,计算过程也比较复杂,往往令学生无所适从。为了使多种累心给的圆锥曲线问题迎刃而解,必须对典型的例题进行深入剖析,挖掘问题的本质并进行适当的转化,不断提高学生思考问题的能力[1~2]。
1 典型问题分析
1.1 提出问题
1.2 问题求解
(1)方法一

(2)方法二


图1 解法二
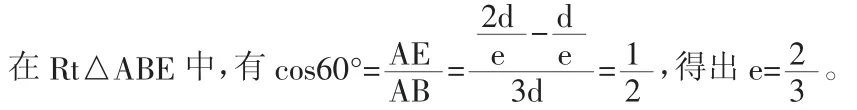
(3)解法三


在这道题中,应用了三种常见的方法,在问题求解的过程中充分应用左焦点F和的信息,解法一的思考较为笼统,从代数方面入手,计算量较为庞大。在解法二中对圆锥曲线的定义进行联想,从几何角度进行入手分析,应用数形结合的方法,简化了问题的求解。在解法三中应用更巧的方法,连线极坐标系下圆锥曲线的统一定义,借助斜率角θ的几何意义进行求解,使问题得到简化[3]。
2 焦点弦公式的推导应用
高中数学直线与圆锥曲线教学的过程中,一直都将求解焦点弦长度的问题作为重点。在求解这类问题的过程中,如果应用传统的代数解法可能导致计算量庞大,字母运算也十分复杂,因此可以充分借助数形结合的方法[4]。
设圆锥曲线的离心率为e,焦点为F,弦AB经过F,斜率为k,且,求证
如图2所示,F为圆锥曲线的焦点,l为圆锥曲线的准线,从A、B两点向l作垂线,垂足分别为D、C。焦点弦AB的倾斜角为α,过点B作AD的垂线与AD或者DA的延长线于点E,则△AEB为Rt△。

图2

3 结束语
圆锥曲线的学习过程中,需要把握几何曲线的基本定义,再将代数和几何的方法结合起来,找出求解焦点弦问题的规律,便于在类似问题中触类旁通,在题解中找出变化,将多种问题联系起来,提高解题效率。
[1]邱昌银.圆锥曲线的准线切线焦点弦的相关性[J].数学通报,2013,26(11):32.
[2]廖应春.圆锥曲线焦点弦的一个性质[J].数学通报,2003,15(4):35.
[3]黄加流.圆锥曲线平行焦点弦性质探究[J].数学教学通讯,2013,59(33):159.
[4]徐 琴.圆锥曲线中离心率e,焦点弦的比λ和弦所在直线的倾斜角α的关系及其应用[J].语数外学习(数学教育),2013,22(10):691.
G633.6
A
1004-7344(2016)05-0036-02
2016-2-2
马翔羽(1980-),女,中教二级,本科,主要从事高中数学教学工作。

