一种并联混合型电能质量调节器注入支路的参数设计方法
楚烺
(广州供电局有限公司番禺供电局 广东省广州市 511400)
一种并联混合型电能质量调节器注入支路的参数设计方法
楚烺
(广州供电局有限公司番禺供电局 广东省广州市 511400)
并联混合型电能质量调节器注入支路的参数对有源部分谐波注入能力有很大影响,研究注入支路参数设计具有重要意义。本文以获得最大谐波注入能力为目标,建立有源部分注入电网的谐波量与注入支路元件参数的数学模型并进行分析求解,得到注入支路最优参数,降低了有源部分容量需求,易于实现装置在高电压大功率场合的应用。
注入支路;参数设计;谐波注入能力
引言
并联混合型电能质量调节器(Shunt hybrid power quality conditioner,SHPQC)能克服无源电力滤波器易与电网阻抗发生谐振的缺陷,且相对有源电力滤波器容量更大[1~6]。
为了能应用于高压大功率场合,应尽可能降低SHPQC有源部分承受的电压,提高有源部分的谐波注入能力[7]。本文研究一种注入支路的参数设计方法,通过建立相关参量间的函数模型并求解得到一组最优的注入支路元件参数,使有源部分谐波注入能力最强,更易实现SHPQC在高压大功率场合的应用。
1 系统的结构及原理
本节介绍一种SHPQC的结构,结合其单相等效电路阐述了基本工作原理。
1.1 系统的结构
所述SHPQC的结构如图1所示,包括由电压型逆变器等构成的有源部分及由多组单调谐无源滤波器构成的无源部分,实现谐波抑制及无功补偿功能。电压型逆变器输出端通过输出滤波电抗器L0与电感L并联再接至隔离变压器原边,隔离变压器副边与一组单调谐无源滤波支路串联后并联接入电网。由C1及L1构成某单次谐波谐振支路,有源部分只向电网注入相应单次谐波。此谐振支路对基波阻抗Z1呈容性,与电感L对电网电压串联分压,电压型逆变器的直流侧电容通过与L交换能量实现直流侧电压Udc的稳定。
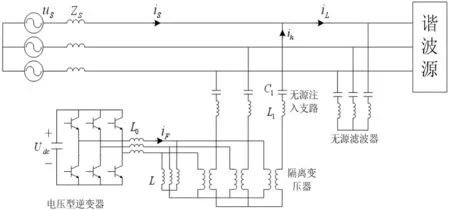
图1 系统主电路结构图
1.2 系统的基本原理
此SHPQC的单相等效电路如图2所示。将负载看做一个电流源,其峰值为ILd,其中负载电流中的谐波电流峰值为ILdh;有源滤波器部分的电压型逆变器的输出等效为一个电压源,其峰值为UF;隔离变压器原边并联的小电感L两端基波分压峰值为UL。设SHPQC有源滤波器部分的输出电感L0两端的电压峰值为Un,即电压型逆变器输出的n次谐波电压,因此,可得有源滤波器部分发出的谐波电流峰值IF如下:

其中ZL0h为电感L0的n次谐波阻抗。
有源部分中逆变器发出的谐波电流IF中的一部分Ih通过单次谐波谐振支路注入电网,另一部分谐波电流流入逆变器交流侧并联的电感L。
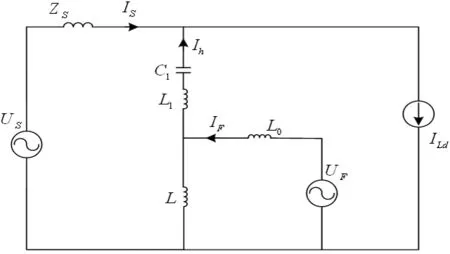
图2 单相等效电路图
2 电压型逆变器及注入支路模型分析
本节主要对有源部分中电压型逆变器及注入支路进行数学模型分析,为有源部分在谐波域的整体数学模型建立提供依据。
2.1 有源滤波器模型分析
如图3所示,设电压型逆变器交流侧输出的相电压瞬时值为Uapf,忽略电网背景谐波电压的影响,则有:
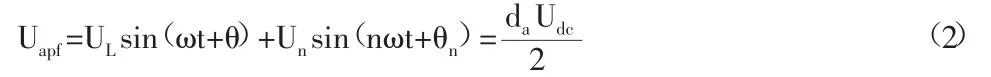
其中θ、θn分别为电感L的基波相位和有源部分逆变器输出谐波电压相位,da为逆变器a相的占空比,Uapf的峰值为UF。
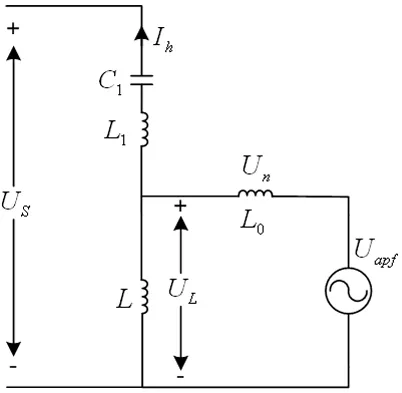
图3 电压型逆变器单相等效电路图
假设电压型逆变器可以承受的直流侧最大稳定直流电压为Udcm,则由上式可知:

当Udc=Udcm时,Unm为电压型逆变器能输出的最大谐波电压峰值,由于谐波电压相位θn不同则其峰值Unm大小也不一样,因此,取所有相位中谐波输出峰值中的最小值(即取UL和Un峰值叠加的情况)作为谐波电压峰值即n次谐波的最大输出能力,即令:

则Unm为电压型逆变器能输出的最大n次谐波电压峰值。
2.2 注入支路模型分析
注入支路单相等效电路如图4所示,可看作由C1、L1及L组成。图中,设单调谐无源滤波支路的基波阻抗为Z1,则有:

由于Z1呈容性,因此,Z1<0。此单调谐无源滤波支路的n次谐波阻抗为Z1h,由于偏谐及元件内阻等原因,无源滤波支路的阻抗为较小的阻感性的阻抗,所以Z1h>0。
注入支路中电感L上的基波电压峰值为UL,则:

由于电网侧电压为高电压,而SHPQC的有源部分不能承受很高的基波电压,因此L的电感值很小,Z1远大于电感L的基波阻抗ZL,整条注入支路的基波阻抗呈容性,即:

所以电感L上的基波电压峰值UL的表达式符号为负号,由UL的表达式可知,ZL越大,电感L两端的基波电压越大,则SHPQC的有源部分承受的基波电压也越大,因此,L的电感值不能太大。
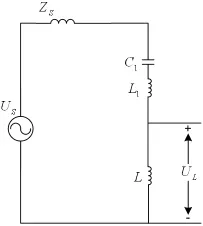
图4 注入支路单相等效图
3 注入支路参数设计
本节建立有源部分注入电网的谐波电流与注入支路元件参数的数学模型,并分析求解,得到使谐波注入能力最强的注入支路元件参数,并阐述了注入支路的具体参数设计步骤。
3.1 数学模型建立
SHPQC谐波分流等效电路图如图5。无源滤波支路的n次谐波阻抗为Z1h,电感L的n次谐波阻抗为ZLh=nZL。若Udc=Udcm时,SHPQC的有源滤波器输出的n次谐波电流峰值为IF,则:

式中ZL0为L0的基波阻抗。
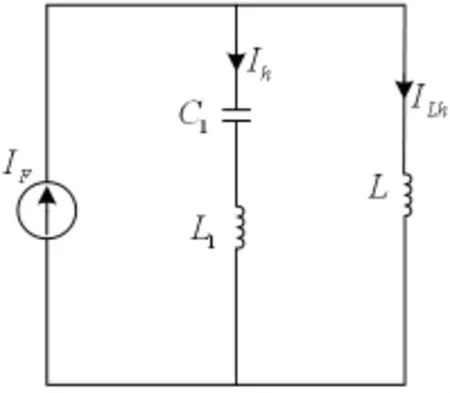
图5 谐波分流等效电路图
Ih为SHPQC有源滤波器输出的n次谐波电流IF中注入电网的谐波电流的峰值,由此可得:

由上式可知当IF不变时,ZL越大,则Ih越,即SHPQC的谐波注入能力越强,因此L的电感值不能太小。将IF的表达式代入上式,得:
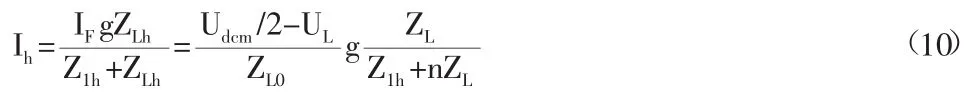
将UL的表达式代入上式,整理可得:
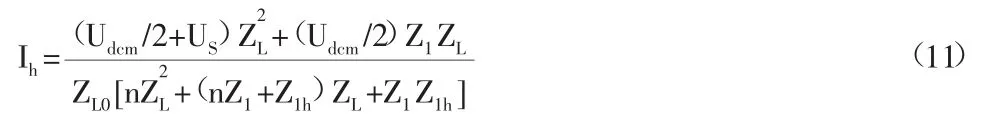
式中,Udcm/2、US为已知量,若n及C1、L1的参数值已知,则Z1、Z1h为已知量,上式右边只有ZL为未知量,因此Ih可以看成ZL的函数Ih(ZL),即有源部分向电网注入的谐波电流大小只与逆变器交流侧并联的小电感L的阻抗ZL有关。
3.2 模型分析求解
本节通过分析求解函数模型Ih(ZL),得到最佳的电感L参数使有源部分注入电网的谐波电流Ih取得最大值。
为了方便模型分析求解,现做如下转化:
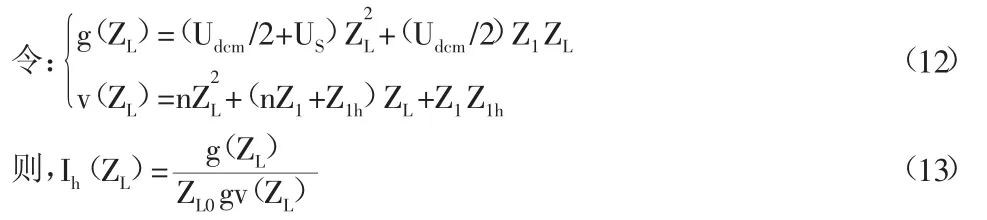
将Ih(ZL)对ZL求导,求出导数I′h(ZL)为零的点,可求出Ih(ZL)的极大值点,即为Ih(ZL)的最大值点,从而可求得对应的电感L的值。由SHPQC的工作原理可得:

在此区间内,v(ZL)≠0,故Ih(ZL)对ZL可导,其导数I′h(ZL)如下:
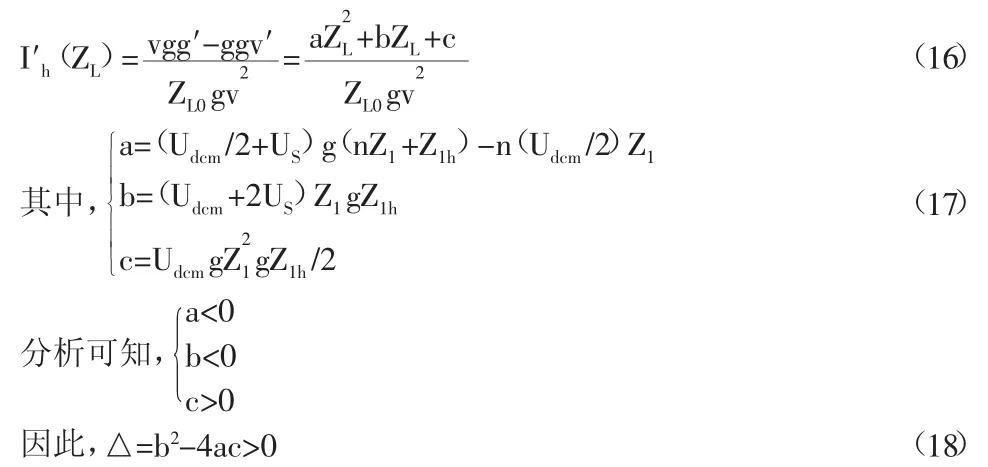
由以上分析可知I′h(ZL)=0存在两个解,如下:

由于b2-4ac>b2,因此可得:

由上述分析可知,Ih(ZL)在ZL=ZL2时取得最大值;代入各项已知参数计算出a、b、c,然后代入上述ZL2的表达式求出ZL2的值,则可得对应的电感L值如下:

此电感值L即为其他条件已知情况下使SHPQC注入电网的n次谐波电流最大的参数值。
3.3 参数设计步骤
本节根据上述理论分析,给出具体的注入支路参数设计步骤。上述理论是假设Udcm/2、US、n、C1、L1均为已知量的条件下,求得的电感值L的表达式,实际参数设计过程中需要先确定注入支路中的其他元件参数量再确定并联电感L的参数。
(1)首先,确定SHPQC注入支路中单调谐无源滤波器的谐振频率n及其所要提供补偿的无功量Q;
(2)根据单调谐无源滤波器的无功量Q确定单调谐无源滤波器中的电容值C1,然后根据其谐振频率n确定电感L1的参数;
(3)US为电网电压峰值,是已知量,根据上述有源滤波器模型分析理论可求得Udcm值;
(4)确定以上各参数值后,将各参数值代入上述电感L的表达式,求出电感L的参数值;
(5)对所设计的参数进行验证,可采用计算和仿真等方法,根据以上设计的L1、C1及L的参数值,分析SHPQC的整条注入支路是否会引起特征次谐波谐振。如果发生特征次谐波谐振,则适当调整电感L的参数值,保证注入支路不会引起特征次谐波谐振的同时尽可能使SHPQC向电网注入的n次谐波电流值最大。
4 结论
本文提出了一种SHPQC注入支路的参数设计方法,以最大化有源部分的谐波注入能力为目标,通过建立相关参量间的函数模型并分析求解得到一组最优的注入支路元件参数,使有源部分谐波注入能力最强,降低对有源部分容量的要求,从而使装置更易实现在高压大功率场合的应用。
[1]罗安.电网谐波治理和无功补偿技术及装备[M].北京:中国电力出版社,2006.
[2]王兆安,杨君,刘进军.谐波抑制和无功功率补偿[M].北京:机械工业出版社,1998.
[3]FUJITAH.Ahybrid active filter for damping of harmonic resonance in industrial power systems.IEEE Trans on Power Electronics,2000,15(2):215~222.
[4]帅智康,罗安,范瑞祥,周柯,唐杰.注入式混合有源电力滤波器的注入支路设计.电力系统自动化,2007,31(5):57~60.
[5]HAFNERJ,AREDSM,HEUMANNK filter appliedto high voltage distribution Power Delivery,1997,12(1):266~272.
[6]程莹,罗安,浣威.注入式混合有源电力滤波器的参数优化设计及其工程应用.电网技术,2010,34(10):53~59.
[7]鞠建永,徐德鸿.混合型有源电力滤波器有源部分容量比较.电能质量管理,2007:34~39.
TM73
A
1004-7344(2016)05-0096-03
2016-2-5
楚烺(1988-),男,湖南人,硕士研究生,主要从事电能质量治理和新能源发电技术的研究。

