复合材料制综框力学性能参数化仿真研究

邱 海 飞

(西京学院 机械工程学院，西安 710123)



复合材料制综框力学性能参数化仿真研究

邱 海 飞

(西京学院 机械工程学院，西安 710123)

摘要:将碳平纹预浸料和单向碳纤维预浸料应用于复合材料层压板设计，采用复合材料壳单元Shell181模拟综框分层结构，建立了针对综框的非对称和对称结构层压板设计方案。静动态特性分析表明，非对称层压板结构综框具有较佳的静力刚度及动力学性能。利用APDL语言开发了综框的参数化建模程序，并以方向参数η和θ为变量，通过零阶算法实现了纤维铺层角度优化设计，结果将综框第1阶自振频率提高了约4.6%，有利于综框减振及织机车速提高。

关键词:综框；复合材料；层压板；优化；铺层角度；力学性能；碳纤维

综框为形成梭口的高速运动部件，对于织机系统的振动及噪声会产生重要影响。随着新型织机的高速高精化发展，对于综框的性能要求也愈来愈高。以往综框多以木质、铁质及铝合金材质为主，随着织机车速的提高，传统综框已不能满足新型现代化织机的生产要求，取而代之的是由复合材料制成的新一代综框[1]。复合材料具有质量轻、强度高及耐热性好等优良特性。大量实践表明，采用复合材料制成的新型综框，能够有效减小织造过程产生的振动及噪声[2]，有利于织机系统的稳定运行、保证生产效率，对于综框性能提升和技术改造具有重要的应用价值。本文将复合材料应用于综框结构设计，研究综框在不同层压板结构下的静动态特性，并实现纤维铺层角度优化，为新型综框研发提供有效手段和技术支持。

1　层压板理论基础

层压板是纤维增强复合材料的常见形式之一，是由一系列单向增强的纤维层铺叠而成。一般情况下，每层纤维厚度约0.2 mm，铺设方向和顺序可根据材料性能自行设定[1]。如图1所示，按照各单层板相对于中面(即距离层压板上下表面相等的面)的排列位置，可将层压板分为对称层压板、非对称层压板及夹芯层压板三大类。制备层压板时要求各层纤维平行铺设，并注入未固化的环氧树脂或其他热固性聚合物基体材料[3]，将各层压板交错黏合就形成了纤维增强复合材料。对于壁板、梁及肋件等层压结构多采用RTM成型工艺。

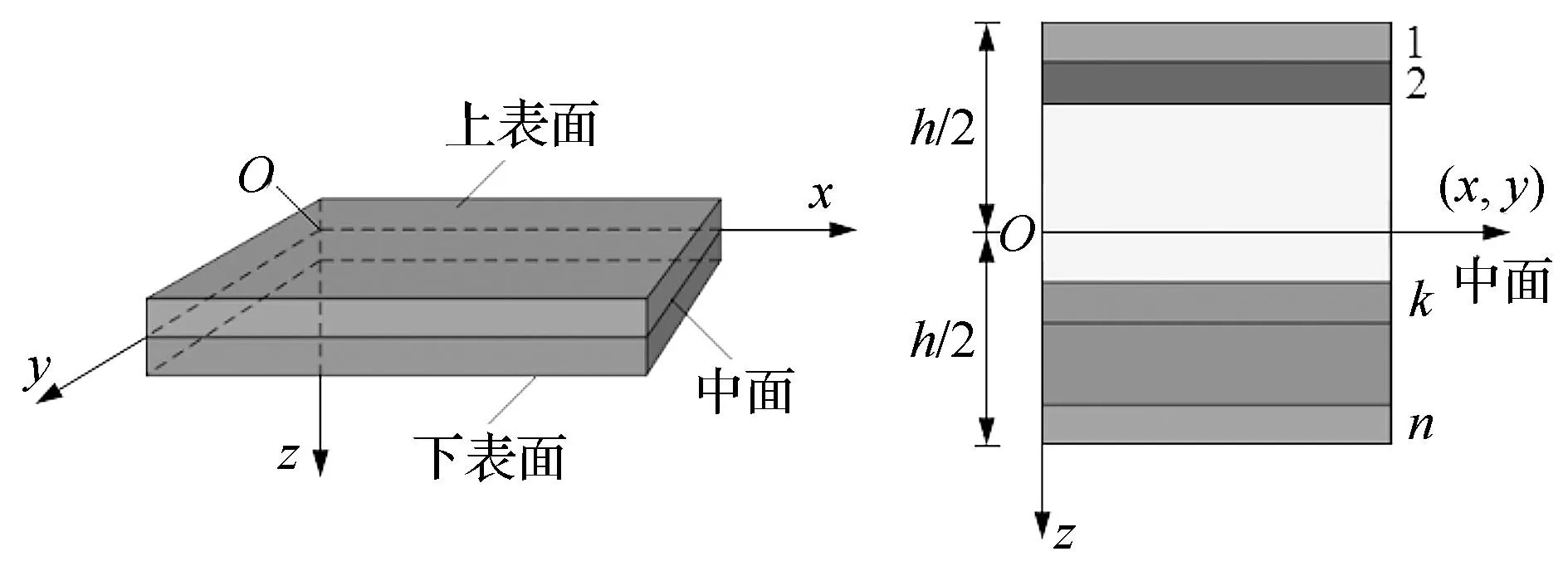
图1　层压板结构Fig.1　Structure of the laminate

经典层压板理论以线弹性和小变形为基本假设，采用宏观力学方法研究各向异性、分层均匀及连续的层压板刚度与强度[3]。根据层压板面内刚度假设：层压板只承受面内力作用，且只引起面内形变，不引起弯曲形变；层压板为薄板结构，即板的厚度远远小于长度和宽度；层压板各单层粘接牢固，具有相同的变形，且层压板厚度方向上坐标为z的任意点的应变都等于中面应变，如式(1)所示。

(1)

如图2所示，Nx、Ny、Nxy为层压板面内力，即层压板内单位宽度上的内力，量纲为Pa或N/m2。

图2　层压板面内力分布Fig.2　Scattergram of internal force in the laminate

(2)

(3)

(4)

根据各向同性单层板本构关系，考虑式(1)～式(4)，可求得面内力和面内应变的关系，如式(5)所示。其中，αij为层压板面内刚度系数，由刚度系数αij构成的矩阵称为刚度矩阵[α]，且有αij=αji。对式(5)作逆变换即可求出层压板面内应变与面内应力的关系式，同时可求得层压板面内柔度系数λij与柔度矩阵[λ]=[α]-1。

(5)

2　综框结构建模

2.1边界条件

对综框结构进行必要简化，忽略综丝夹、穿综杆及综丝等零部件，如图3所示在下横梁底端设置两个固定铰支点，距离侧档内侧210 mm。综框运动过程中会受到经纱张力作用，为了便于计算与分析，将纱线张力等效至下横梁，通过均布载荷q近似代替综框受到的经纱张力。

图3　等效边界条件简图Fig.3　Sketch of the equivalent boundary conditions

以中平布纯棉织物为依据，纱线线密度为28 tex，则作用于综框的最大集中载荷Fmax如下式所示，

(6)

式中：ρf为织物经密，251.5根/10 cm；Pmax为单根纱线在垂直方向的最大张力值，约为0.075 N[4]。

由式(6)计算得Fmax=433.84 N，则均布载荷q=Fmax/2.3=188.63 N/m。

2.2层压板结构设计

铺层纤维的种类、层厚、铺设方向及积分点数等均会影响复合材料层压板的性能[5]。采用碳平纹预浸料和单向碳纤维预浸料设计综框层压板，其密度分别为1 452 kg/m3和1 560 kg/m3，材料力学性能见表1[2]。根据层压板铺层设计工艺，一般多选用0°、45°、-45°和90°四种铺层角，且连续相同的铺层尽量不超过2层。设计2种层压板结构铺层方案，即如图4所示非对称铺层和对称铺层：非对称层压板纤维铺设方向为[0/45/-45/90]，对称层压板纤维铺设方向设为[0/45/-45/902/-45/45/0]。

表1　材料属性

图4　综框层压板设计方案Fig.4　Design scheme of the laminate for heald frame

利用APDL语言编写综框(230 cm幅宽)的参数化建模程序，采用4节点24自由度单元Shell181模拟综框层压板结构。Shell181是典型的复合材料仿真单元，其模拟状态与计算结果均能有效接近实际情况，具有较高的仿真精度及等效性，故常被用于分析薄至中等厚度的壳结构，并可模拟分层的复合壳及夹层结构。综框层压板结构和有限元建模数据见表2。在参数化基础上计算和建立综框有限元模型，如图5所示，对横梁、导板及侧档的接触位置进行网格细化与局部控制，在下横梁支点处设置节点位移约束，将x与y方向位移设置为0，并在下横梁上端施加均布载荷q。

表2　层压板建模数据

图5　基于参数化的综框有限元模型Fig.5　Parametric finite element model of heald frame

3　静动态性能

3.1静力学分析

综框在静态载荷作用下的变形如图6所示，非对称铺层主要是综框整体的扭转变形，最大形变量约3.23 mm，出现在侧导板上端部位置，另外在下横梁与侧档交叉接触区域也存在较大变形；对称铺层主要表现为下横梁弯曲变形，中导板两侧附近形变量最大，约0.051 mm。非对称铺层与对称铺层的最大应力值分别为1.02 MPa和1.08 MPa，主要集中在Node180和Node58节点处，即图7所示的下横梁下端边沿位置的三角形区域，应力值由该三角形区域向外扩散依次减小。根据有限元静力学分析结果，以非对称铺层层压板设计的综框具有较强的抗变形能力和静态承载能力，即在相同静态载荷作用下，非对称铺层综框的刚度与强度要优于对称铺层。

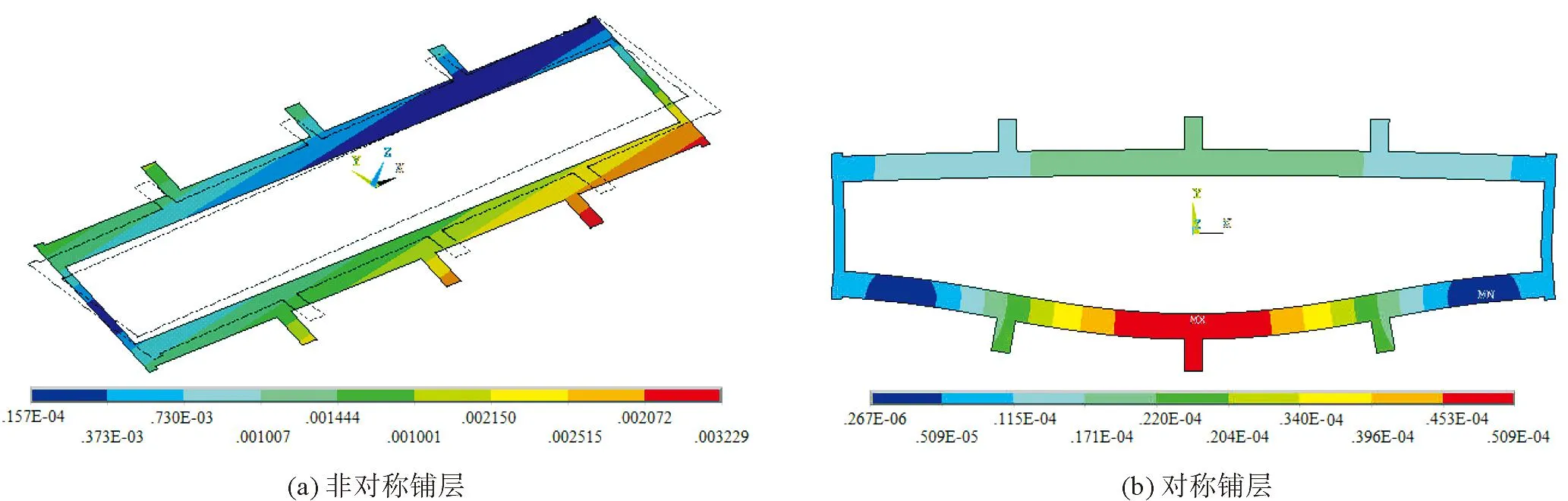
图6　静力变形图解Fig.6　Static deformation diagrams

图7　最大应力分布云Fig.7　Distribution chart of the maximum stress

3.2自振频率及振型

根据振动理论，结构的自由振动方程如下，

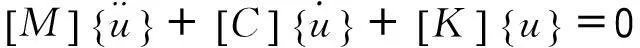
(7)

其中[M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，{u}为节点位移向量。自由模态分析时可忽略阻尼影响，通过线性变换实现式(7)的静力解耦与惯性解耦，即将无阻尼自由振动方程从物理坐标转化至相互独立的模态坐标，并获得如下所示频率方程，

(8)

其中λ为系统特征值[6]，求解式(8)即可计算出结构的模态频率及振型。

采用Block Lanczos法提取综框在无约束状态下的前3阶模态频率与振型结果见表3。由表3可知，两种不同铺层综框的低阶模态频率较为接近，其中非对称层压板综框的第1阶模态频率(基频)为41.986 Hz，略大于对称层压板综框的41.128 Hz，说明非对称铺层综框具有相对较强的抗振能力。由振型图解可知，两种层压板结构综框的第2阶、第3阶振动模式相似，均表现为扭转振动和弯曲振动；不同的是，两种铺层方案的第1阶振动模式正好相反，即非对称铺层综框主要为上下横梁的外侧弯曲振动，而对称铺层综框则主要为上下横梁的内侧弯曲振动。

表3　不同层压板结构下的综框模态特性

4　铺层角度优化

对非对称层压板纤维铺层角度进行优化，复合材料初始纤维铺层方向为[0/45/-45/90]，保持水平方向(0°)和垂直方向(90°)的纤维铺设方向不变，以变量η、θ分别表示45°及-45°的角度变化，若按照逆时针方向确定铺层角度，则-45°应转化为315°，如图8所示。设计变量η和θ的取值范围定义为：η∈(15°，75°)；θ∈(285°，345°)。

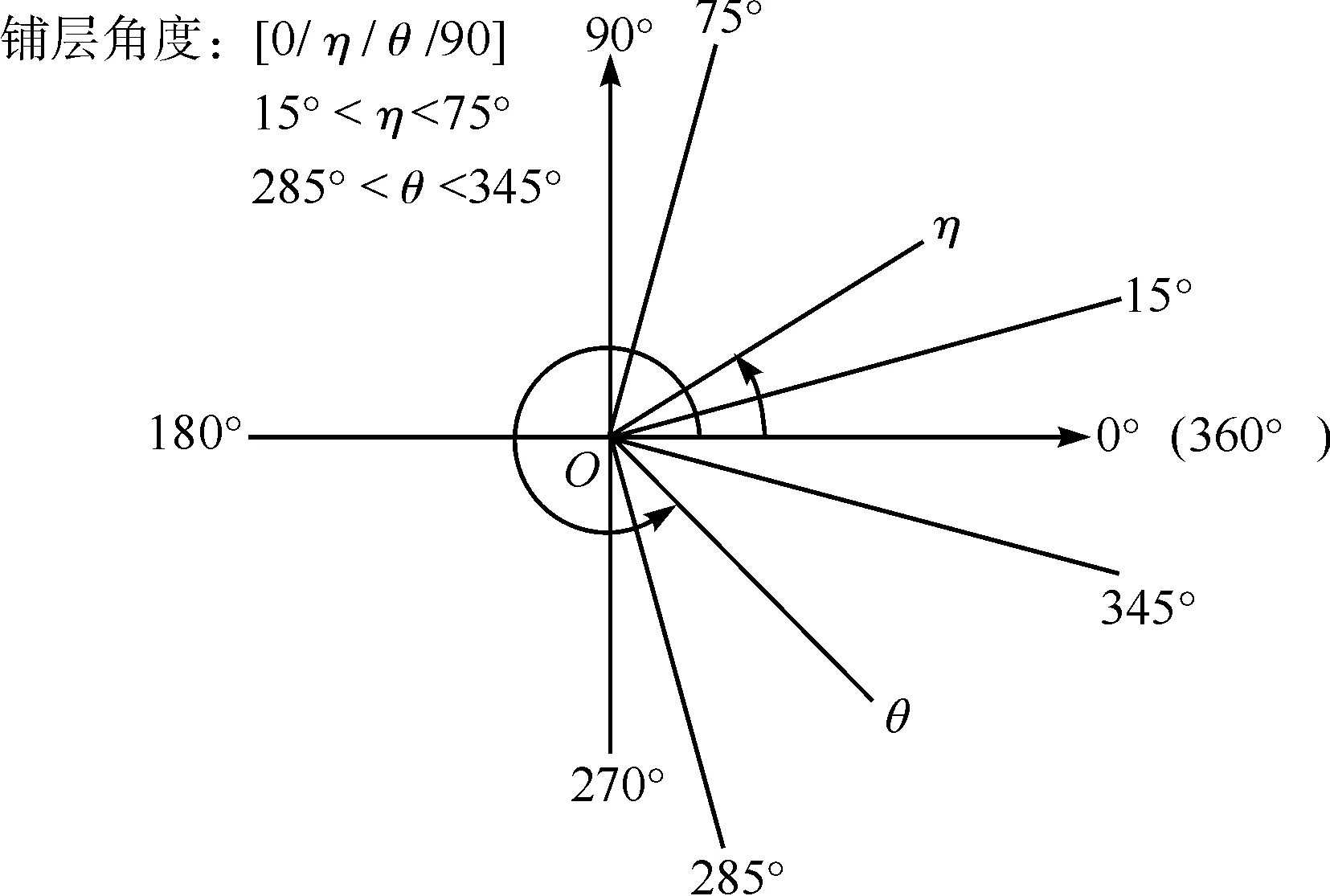
图8　层压板纤维铺层角度Fig.8　Layer angles of the laminate fiber

为了降低综框在织造过程中的振动与噪声，要求综框具有较强的刚度及抗振能力，故应尽量提高综框的自振频率。根据振动理论，基频f0是衡量结构动力学特性的重要参数，故在优化层压板结构时要求综框第1阶模态频率尽量最大，即以提高基频f0为优化设计目标。由动力学计算结果可知，非对称层压板结构综框的基频f0=41.986 Hz，故定义优化目标函数如下，

(9)

其中f0(η，θ)为设计变量η和θ的函数，f0i为基频的第i次优化计算值。由于ANSYS系统以目标变量最小化为优化原则，故定义差值关系式δ(η，θ)=65-f0(η，θ)，即执行优化计算时要求δ(η，θ)为最小。

采用零阶算法执行优化过程，通过变量η、θ的采样组合产生不同的纤维铺层方向，由此实现多个优化序列下的目标函数f0(η，θ)迭代计算。由图9和表4可知，优化后的变量η、θ值增大至74.87°、344.74°，比初始值分别提高了66.38%和9.44%，说明纤维铺层角度发生明显变化。将θ值换算为锐角形式，则优化后的非对称层压板铺层角度为[0/74.87/-15.26/90]。当执行第9次优化序列时，目标函数f0(η，θ)达到最大值，对比可知，优化后的基频f0为43.9171 Hz，比优化前增大了约4.6%。可见，优化后的综框抗振性能得到进一步增强，符合优化设计初衷。

图9　优化设计过程曲线Fig.9　Process curves of optimization design

优化变量优化前优化后变化率/%η/(°)45.0074.8766.38 θ/(°)315.00 344.74 9.44f0/Hz41.9943.924.60

5　结　语

复合材料综框是未来新型综框的主要发展方向。通过将碳纤维复合材料应用于综框设计，明确了层压板结构的力学特性、铺层原理及实现方法。根据两种铺层方案研究结果可知，非对称铺层结构具有较佳的静动态特性。另外，通过纤维铺层角度优化，使综框基频增大了约4.6%，进一步提高了复合材料综框的自振频率，有效降低了织机系统的振动和噪声，为新型综框的研制及性能改进提供了重要依据。

参考文献：

[1]邱海飞,王益轩,吴松林.新型碳纤维复合材料综框的铺层设计与动力学特性研究[J].科学技术与工程,2014,14(7):168-172.

QIU Haifei, WANG Yixuan, WU Songlin.Layering design and dynamic characteristics study for heald frame maded by new type composite of carbon-fibre[J].Science Technology and Engineering,2014,14(7):168-172.

[2]霍福磊.综框用混杂夹芯结构复合材料的设计与制备[D].天津:天津工业大学,2012:8-15.

HUO Fulei.Design and Peparation for Composite Material in Mixed Sandwich Structure Used for Heald Frame [D].Tianjin:Tianjin Polytechnic University,2012:8-15.

[3]张以河.复合材料学[M].北京:化学工业出版社,2011:58-61.

ZHANG Yihe.Composite Materials [M].Beijing:Chemical Industry Press,2011:58-61.

[4]邱海飞,王益轩.基于虚拟样机技术的经纱张力仿真与分析[J].纺织学报,2011,32(1):119-123.

QIU Haifei, WANG Yixuan.Simulation and analysis of warp tension based on virtual prototyping[J].Journal of Textile Research,2011,32(1):119-123.

[5]谭志勇,闵昌万,龙丽平.先进复合材料的结构动力学设计与分析技术探讨[J].强度与环境,2011,38(3):24-28.

TAN Zhiyong, MIN Changwan, LONG Liping.The technology of dynamics design and analysis for the structure of advanced composite material[J].Structure & Environment Engineering,2011,38(3):24-28.

[6]邱海飞,王益轩,刘欣.综框模态频率优化设计[J].机械设计,2012,29(5):35-38.

QIU Haifei, WANG Yixuan, LIU Xin.Optimal design for frequency of heald frame[J].Journal of Machine Design,2012,29(5):35-38.

[7]陆综源.织造经纱张力浅论[J].纺织器材,2015,42(1):64-66.

LU Zongyuan.My tension view on warp tension[J].Textile Accessories,2015,42(1):64-66.

[8]房超,陈宁,徐茗娟.综框材料和结构的专利技术综述[J].轻纺工业与技术,2015(2):23-25.

FANG Chao, CHEN Ning, XU Mingjuan.Technical review of the patent for heald frame’s material and structure[J].Light and Textile Industry and Technology,2015(2):23-25.

[9]赵梅,王益轩,路超,等.三维正交织机双向开口机构设计[J].产业用纺织品,2015(2):29-34.

ZHAO Mei, WANG Yixuan, LU Chao, et al.Design of the dual-direction shedding mechanism of three-dimensional orthogonal loom[J].Technical Textiles,2015(2):29-34.

[10]杨彩云,李嘉禄.复合材料用3D角联锁结构预制件的结构设计及新型织造技术[J].东华大学学报(自然科学版),2005,31(5):53-58.

YANG Caiyun, LI Jialu.The strucural design and new weaving technique of 3D angle-interlock preforms for compo sites[J].Journal of Donghua University(Natural Science),2005,31(5):53-58.

DOI:10.3969/j.issn.1001-7003.2016.04.007

收稿日期:2015-10-14; 修回日期:2016-03-14

基金项目:陕西省教育厅科研计划资助项目(15JK2177)；西京学院科研基金项目(XJ150216)

作者简介:邱海飞(1983—)，男，讲师，硕士，主要从事机械系统动态设计、虚拟样机技术的研究。

中图分类号:TS101.91

文献标志码:A

文章编号:1001-7003(2016)04-0035-06引用页码:041107

Parametric simulation research on mechanical property of heald frame made by composites

QIU Haifei

(College of Mechanical Engineering, Xijing University, Xi’an 710123, China)

Abstract:In this paper, carbon plain pre-soak material and unidirectional carbon fiber pre-soak material were applied to the design of composite laminate.Layer structure of heald frame was simulated by composite element Shell181, and then design scheme of asymmetrical and symmetrical laminate for the heald frame were set up.The analysis results of static-dynamic characteristics shows that heald frame with asymmetrical laminate has good static stiffness and dynamic properties.Parametric modeling program of the heald frame is developed through APDL Language, and optimization design of the fiber layer angles is carried out based on zero-order method where orientation parameters are η and design variables are θ, which increased the natural frequency of the first layer in heald frame by 4.6%, thus making it favorable for vibration attenuation of heald frame and speed up of the loom.

Key words:heald frame; composite; laminate; optimization; layer angle; mechanical property; carbon fiber