齿轮传动双转子固有频率影响因素分析
车永强,王 鑫,吕海祯,刘 欢,张善鹏
齿轮传动双转子固有频率影响因素分析
车永强1,王鑫1,吕海祯1,刘欢1,张善鹏2
(1.国网山东省电力公司电力科学研究院,济南250003;2.山东中实易通集团有限公司,济南250003)
根据有限元法,应用MATLAB软件,考虑弯扭耦合振动,建立齿轮—转子五自由度运动模型,通过求解系统运动微分方程,分析了齿轮啮合刚度、齿轮传动比和轴承刚度对齿轮—转子系统固有频率的影响。
齿轮传动双转子;齿轮啮合刚度;轴承刚度;传动比;固有频率
0 引言
齿轮传动是旋转机械中应用最广泛的传动机构,它工作可靠、传动比恒定,能满足现代工业高速度大功率传动的要求[1]。因此,齿轮传动的转子系统获得了广泛的应用并已成为转子系统中重要的一类传动。
齿轮传动双转子系统,既有弯曲振动,又有扭转振动。由于转子之间的齿轮啮合作用,各转子的弯振和扭振产生了耦合,各转子的振动也不再相互独立,而是相互影响、相互制约的,齿轮、轴承和转子已成为系统不可分割的组成部分。因此在分析带齿轮的高速旋转机械时,应该考虑齿轮的啮合作用,并把齿轮副作为转子系统的一部分来进行动力特性分析[2]。
应用MATLAB软件,考虑弯扭五自由度,推导轴单元、圆盘单元、齿轮副单元和轴承单元的运动微分方程,耦合得到齿轮—转子的运动微分方程,通过求解该微分方程,研究齿轮啮合刚度、齿轮传动比和轴承刚度对齿轮-转子系统固有频率的影响。
1 齿轮传动双转子模型
图1为齿轮传动的双转子系统结构示意图,图中转子1为主动转子,转子2为被动转子,两转子之间通过齿轮副连接。该齿轮传动转子模型结构参数见表1、表2。应用转子动力学的有限元理论,将该模型离散成为轴承、轴、圆盘、齿轮副等单元,在每个单元上设置一定节点,单元与单元之间通过节点连接。对于轴单元,设置2个节点,分别位于轴单元的两个端点;对于圆盘单元,设置1个节点,位于圆盘的中心;对于轴承单元,设置1个节点,位于轴颈中心。然后对每个单元进行分析,得到各单元的运动微分方程,最后通过广义坐标,将所有单元的运动微分方程组合到一起。

图1 齿轮传动的涡轮—发电机系统结构
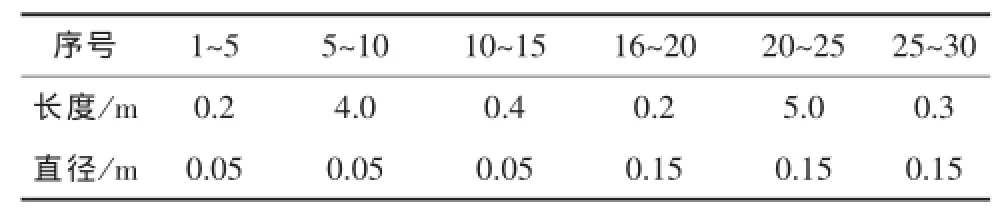
表1 系统各轴段的长度和直径
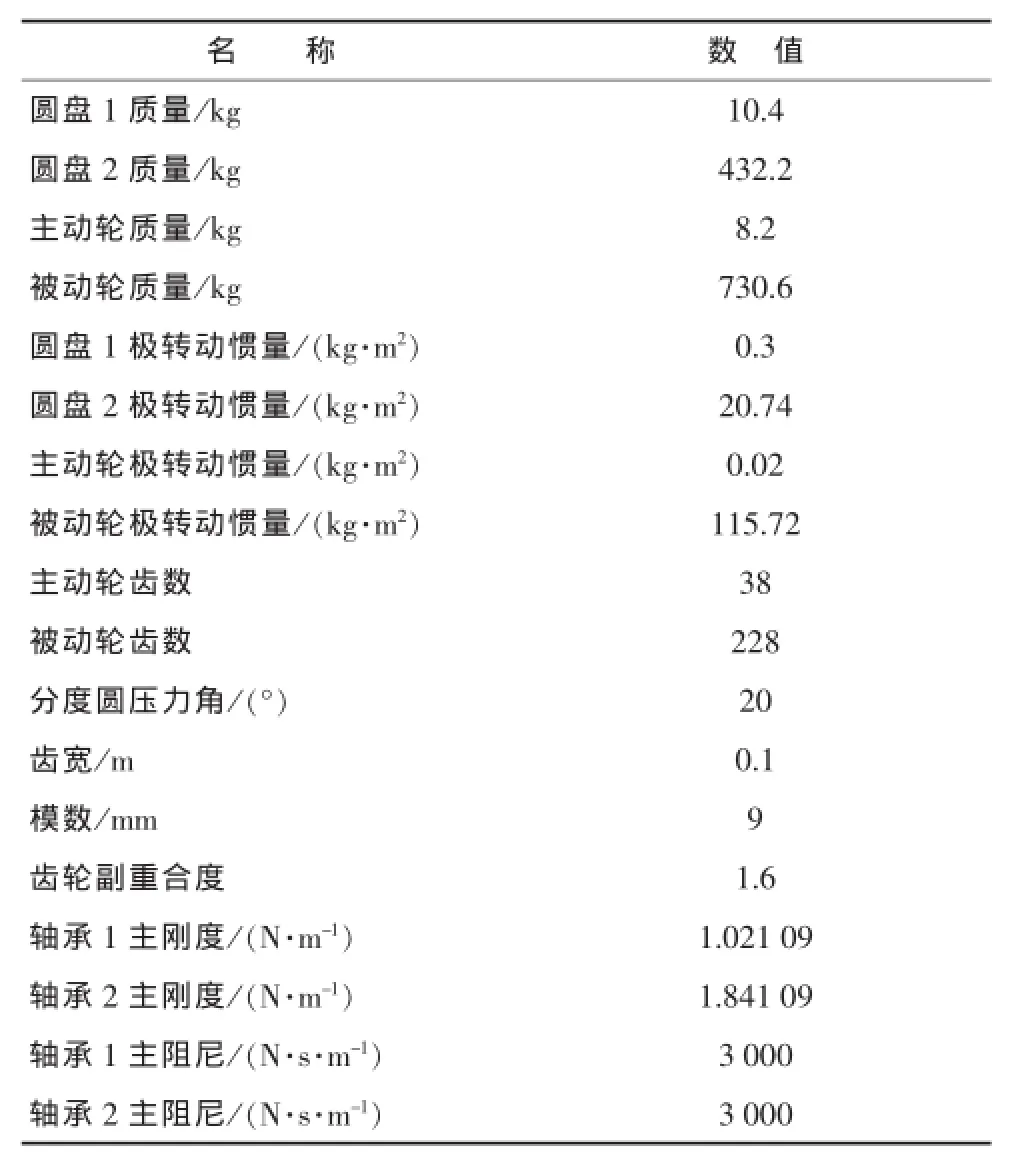
表2 系统齿轮、圆盘、轴承结构参数
考虑系统的弯扭耦合振动[4],每个节点都有2个平动、2个弯曲、1个扭转共5个自由度,则该节点的广义坐标可以表示为式中:x、y、θx、θy为x、y方向的平动位移和弯角;φ为轴向的扭角。

应用拉格朗日方程,得到各单元的运动微分方程[3],然后组合,得到了齿轮—转子系统的运动微分方程

式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为广义力矩阵。
2 转子系统模态分析
转子临界转速是指与转子及其支承系统的横向或扭转振动固有频率相同的转速。转子在临界转速附近工作时,转轴会产生很大的挠度或扭转角,同时发生强烈振动,使机件破坏。转子在远离临界转速运转时,振幅很小,工作平稳可靠[5]。只有避开转子的临界转速才能保证转子稳定运行。所以计算临界转速具有重要的意义。
计算转子的临界转速,实际上就是求微分方程的齐次解,此时系统的广义力F不予考虑,可认为0,由方程(2)得,单转子系统的运动微分方程的齐次式为

方程(3)是一个二阶运动微分方程,可以通过变换将其转化为一阶运动微分方程,引入状态向量

则方程(3)可变换为
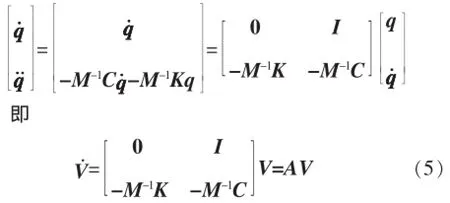
式中:0和I分别为0矩阵和1矩阵,且大小等于整体质量矩阵。
降阶后的方程(5)为一阶齐次运动微分方程,A为特征矩阵。通过求解特征矩阵A的特征值就可以得到齿轮—转子系统的临界转速[6]。应用MATLAB软件求解特征矩阵A的特征值和特征向量,得到的都是复数,包含实部和虚部。其中,特征值的虚部代表的是某一转速下齿轮—转子系统的同步涡动频率,包括弯振固有频率和扭振固有频率;特征值的实部代表系统的稳定性。特征向量也分弯振和扭振,与弯振对应的特征向量的实部和虚部,分别代表x、y方向的振幅,与扭振对应的特征向量的虚部,代表沿轴向的扭角。
同时,为准确区分转子的弯振固有频率和扭振固有频率,需要做出Campbell图。Campbell图是一种用来判断转子工作时是否出现共振,以确定转子出现共振的频率和阶次、共振转速和激励源的工程解法。Campbell图中横轴代表转子系统的转速、纵轴代表弯振和扭振固有频率,Ω=ω的斜线表示转子转速等于涡动转速。如果Ω=ω线和固有频率线相交,表示可能会发生共振。在Campbell图中,当考虑系统的陀螺力矩时,弯振的正向涡动线与反向涡动线成对出现;不考虑系统的陀螺力矩时,弯振的正向涡动线与反向涡动线重合,为一水平直线。而陀螺力矩对扭振没有影响,因此扭振涡动线始终表现为一条水平直线。
3 固有频率影响因素分析
齿轮传动双转子的不平衡响应最大振幅波峰一般发生在齿轮—转子系统的各阶弯振固有频率和扭振固有频率处,因此,关注对齿轮—转子系统的弯振固有频率和扭振固有频率的影响因素,更有实际意义。
3.1齿轮啮合刚度的影响
齿轮啮合刚度是指齿轮啮合时轮齿抵抗变形的能力。啮合刚度直接影响齿轮副单元的刚度,从而影响齿轮—转子系统的固有频率。为分析齿轮啮合刚度对系统固有频率的影响,通过改变啮合刚度,数量级从102到1016,分别做出了对应的弯振固有频率和扭振固有频率的Campbell图。图2给出的是随齿轮啮合刚度变化的齿轮—转子系统扭振固有频率变化图;图3给出的是随齿轮啮合刚度变化的齿轮—转子系统弯振固有频率变化图。
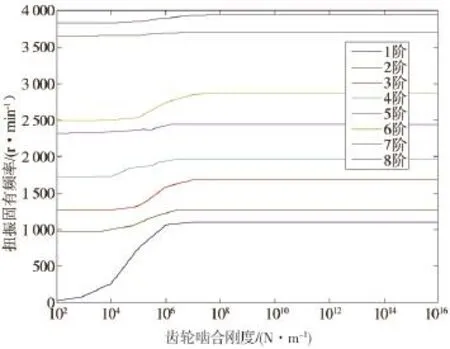
图2 扭振固有频率—齿轮啮合刚度图
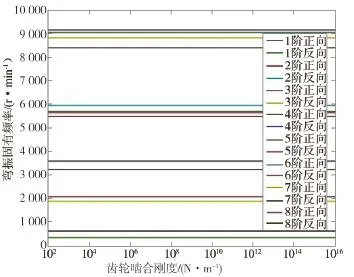
图3 弯振固有频率—齿轮啮合刚度图
从图2看出,随着齿轮啮合刚度的增加,系统的扭振固有频率也在增大。这是因为齿轮啮合刚度的增加,提升了齿轮—转子系统的整体扭转刚度,系统的各阶扭振固有频率也就随之增大。其中1阶扭振固有频率的增幅最大,说明系统的1阶扭振固有频率对啮合刚度最敏感。但当啮合刚度增大到108以后,所有扭振固有频率不再变化,都表现为一条水平直线,这是因为此时的齿轮啮合刚度已经远高于系统本身的刚度,齿轮啮合刚度对系统的影响已趋于稳定。从图3看出,随着齿轮啮合刚度的变化,系统弯振固有频率几乎没有变化。这说明齿轮啮合刚度主要影响的是系统扭振固有频率,而对系统弯振固有频率则没有影响。
3.2齿轮传动比的影响
图4(a)和图4(b)分别给出了传动比为1和10时,随转速增加,系统弯振固有频率和扭振固有频率的变化曲线。对比两图可以发现,齿轮传动比的不同,并不影响扭振涡动线,即始终为一条水平直线,而部分弯振涡动线变化较大,另一部分弯振涡动线基本不变,尤其在传动比为10时,正向涡动线与反向涡动线更加偏离。

图4 不同传动比下的系统Campbell图
齿轮传动比的改变,实际上是改变了从动转子2的工作转速,从而改变了转子2的陀螺效应,对转子2影响更大;而转子1的转速和陀螺效应并没有变化。那么图4(a)和图4(b)中不发生变化的弯振涡动线对应的应该是转子1,正反向涡动线偏离更大的对应的应该是转子2。
当主动转子1转速为0时,齿轮传动比的改变,对转子2的转速没有影响,并不会引起系统固有频率的改变。因此为分析传动比的影响,假定转子1的转速为5 000 r/min,在这个转速下,通过改变齿轮传动比,从1/6到10,做出了转子2的前5阶同步正向和反向涡动频率的变化图,如图5所示。
从图5中可以看出,随着传动比的增加,转子2的同步正向涡动频率线与同步反向涡动频率线的偏差越来越大。因此齿轮传动比的增加,一方面提高了转子同步正向涡动固有频率,另一方面减小了转子同步反向涡动固有频率。
3.3轴承刚度的影响
为便于分析,所建立的齿轮—转子系统模型中的4个轴承的刚度数量级一致,均为109N·m-1。通过改变轴承刚度,数量级从102N·m-1到1014N·m-1,分别做出了对应的弯振固有频率和扭振固有频率的Campbell图。图6为随轴承刚度变化,齿轮—转子系统在同步涡动线上的弯振固有频率变化图;图7为随轴承刚度变化,系统的扭振固有频率变化图。

图5 转子2的前5阶涡动频率随传动比的变化
从图6中可以看出,当轴承刚度为102~108区间时,随轴承刚度的增加,系统的弯振固有频率也增加,这是因为轴承刚度的增加,提高了齿轮—转子整个系统的刚度;但当轴承刚度增加到109之后,系统的弯振固有频率,不再发生变化,趋于稳定,这是因为此时轴承刚度已大于转子本身的刚度,在这个数量级下,系统的弯振固有频率较稳定。
从图7中可以看出,为随着轴承刚度的增加,系统的扭振固有频率并没有发生变化,这是因为,轴承刚度的变化,并不会引起系统扭转刚度的变化。

图6 系统弯振固有频率—轴承刚度图
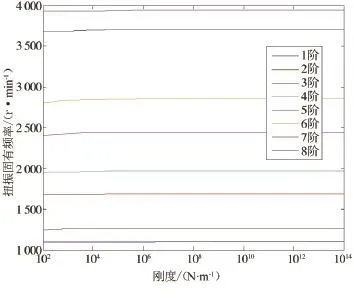
图7 系统扭振固有频率—轴承刚度图
3.4其他齿轮参数的影响
齿轮参数的改变,影响齿轮啮合刚度的大小。通过计算发现,在传动比不变的前提下,改变齿轮的齿数、模数、压力角、重合度、厚度,会引起齿轮啮合刚度较小的变化。但由于所建立的齿轮—转子系统模型的啮合刚度的数量级为109,在这个数量级下,系统弯振固有频率和扭振固有频率都相对较稳定,不会发生太大变化。因此,可以认为齿 为变化的范围较小,对齿轮啮合刚度影响很小,可认为对系统固有频率影响很小。
[1]李良军.机械设计[M].北京:高等教育出版社,2010.
[2]李国平.齿轮—轴承—转子系统振动特性的研究[D].长春:东北大学,2005.
[3]车永强,徐静霞,钱小东,等.齿轮传动转子系统弯扭耦合振动研究[J].机电工程,2012,29(6):632-635,649.
[4]蒋庆磊,吴大转,谭善光,等.齿轮传动多转子耦合系统振动特性研究[J].振动工程学报,2010,23(3):254-259.
[5]钟一谔.转子动力学[M].北京:清华大学出版社,1987.
[6]韩玉强,石守红,张锁怀.齿轮耦合对转子-轴承系统固有特性的影响[J].机械科学与技术,2003,22(1):66-70.
Influencing Factors Analysis on the Natural Frequency of Geared Double Rotor System
CHE Yongqiang1,WANG Xin1,LV Haizhen1,LIU Huan1,ZHANG Shanpeng2
(1.State Grid Shandong Electric Power Research Institute,Jinan 250003,China;
2.Shandong Zhongshi Yitong Group Co.,Ltd.,Jinan 250003,China)
Based on the finite element method of MATLAB software,5 degree freedom motion model of the gear-rotor is established considered coupled bending and torsional vibration.By solving differential equations of motion,the influence of the gear mesh stiffness,gear ratio and bearing stiffness on the natural frequency of the gear rotor system is analyzed.
geared double rotor;gear mesh stiffness;bearing stiffness;gear ratio;natural frequency
TH132.4
B
1007-9904(2016)06-0056-04
2016-02-22
车永强(1986)男,从事汽轮机节能与热试研究工作。

