晶粒生长的双区域动力学蒙特卡洛模拟

张　平,　李建华,　李洪林

(华东理工大学信息科学与工程学院,上海 200237)



晶粒生长的双区域动力学蒙特卡洛模拟

张平,李建华,李洪林

(华东理工大学信息科学与工程学院,上海 200237)

现有的动力学蒙特卡洛方法模拟晶粒生长过程的结果与理论计算值之间大多存在偏差,其中重要的原因是现有方法大多采用只适用于计算小角度晶界Read-Shockley公式。针对此问题,本文提出了一种对大、小角度晶界都适用的双区域动力学蒙特卡洛模拟方法。该方法通过基于势函数的格点能量获得取向概率,从而避免使用Read-Shockley公式。为了解决引入势函数导致计算量大的问题,划分动力学蒙特卡洛的单区域结构为晶界区域和非晶界区域的双区域结构,并将势函数的计算限制在晶界区内,从而减少了计算时间。实验模拟结果表明:与传统的和改进的动力学蒙特卡洛方法相比,双区域动力学蒙特卡洛方法的微观组织演变更符合晶粒生长特征,晶粒生长指数也更接近理论值。

动力学蒙特卡洛; 晶粒生长; 微观组织; 晶粒生长指数

晶粒生长是影响多晶材料物理和机械性能的一个重要过程。目前,已有很多种理论和实验方法用于研究晶粒生长,其中比较常见的方法有相场法[1]、蒙特卡洛(Monte Carlo)法[2]和动力学蒙特卡洛(Kinetic Monte Carlo,kMC)法[3-6]。

动力学蒙特卡洛方法是用于模拟自然界中某些随时间演变过程的一种蒙特卡洛方法[7]。由于动力学蒙特卡洛方法的基础是随机性,使得它非常适合描述某些过程,例如空位扩散、生长、化学反应等。

众多学者在用动力学蒙特卡洛方法模拟晶粒生长时均使用Read-Shockley 模型[8]计算晶界能。该模型由Read和Shockley于1950年提出[9],由于其只适用于小角度,对大角度晶界的计算结果往往偏离真实值。国内外的学者对此都提出了改进方法。张继祥等[10]提出将大角度晶界的能量设为常数;Mallick等[11]在计算小角度晶界能时用Read-Shockley模型,在计算大角度晶界能时尝试将公式进行标准化扩展,虽然扩展公式的变化趋势符合原公式,但是计算得到的晶界区的能量却与原来的值存在差别。虽然已有学者对Read-Shockley模型提出了改进,但是改进方法对于大角度晶界的计算仍然无法得到理想值。

为此,本文提出将势函数引入晶界区格点能量的计算中,避免Read-Shockley模型的局限性,模拟了各向异性条件下晶粒生长的组织结构演化过程。

1　晶粒生长的kMC模拟

1.1晶粒生长

多晶材料中的晶粒生长是一个自发的过程,可以形象地形容为“大晶粒吞并小晶粒”。由于实际晶粒组织的复杂性,对晶粒的形状简化假设都是基于统计平均的方法。Hillert[12]从统计角度出发,提出晶粒长大模型如下:

(1)

其中:M为晶界迁移率;γ为晶界区的能量;R为晶粒半径;Rc为临界半径;α为常数。实验研究[13]和计算机模拟[14]结果表明,晶界区的能量可以改变晶粒的生长行为。传统的计算晶界区能量的方法是采用Read-Shockley公式,见式(2)。

(2)

其中:θ′为晶粒间取向差,常设置为0到π的某个值;θ为晶界夹角;J为大角度晶界能。

公式中的实际晶粒取向通过如下方法与模拟中随机生成的取向数相对应[10]:在直角坐标系中,对于二维中的晶粒有0～360°的取向,由于晶粒取向的特殊性可表示为0～180°,因此用180个取向数表示,每个取向数代表一个对应的晶体取向。晶界两侧的取向差Δθ(即晶界夹角)的计算如下:

Δθ=

(3)

其中:SG1和SG2为晶界两侧格点内的取向数;Q为总取向数。

1.2晶粒生长的传统动力学蒙特卡洛方法

在介观尺度观察晶粒生长的过程中,可以将该过程看成是晶粒从一种状态到另一种状态的跃迁,而kMC是适用于系统状态转变的方法。kMC是由Bortz等[15]在蒙特卡洛算法基础上提出的NFW(N-Fold Way)方法演化而来,目前已有十几种不同版本的kMC方法。

kMC方法的具体思路是:首先确定系统中发生的事件的个数M以及每个事件发生变化的速率kij,然后由[0,1]之间的随机数确定从初始态到下一个状态发生变化所需的时间τ,以及选择要发生的事件,发生相应的变化后系统将从初始态跃迁到下一个状态,如此反复,直到所设定的限制条件。跃迁时间的计算公式如下:

(4)

在晶粒生长中,动力学蒙特卡洛方法首先将多晶体材料的连续微观组织结构映射到离散的二维网格上,即对于每个网格点随机赋予一个整数值,具有相同整数值的相邻网格点表示一个晶粒,不同整数的交界作为晶界。具体的生长算法如下:

(2)每个事件(网格点)有相应的发生转换的概率ρ,所有事件组成一个概率事件列表,

(5)

其中:常数γmax和Mmax分别表示晶界移动的最大能量和迁移率;ΔE表示晶界区格点能量;Ts为模拟温度。

(3)依次选取每个事件尝试新取向,计算概率,然后在[0,1]内随机产生一个分布均匀的数ε，ε=ερ0，如果ρ>ε，则表示该网格点的新取向是可以被接受的,也就表示重新取向可被接受,则晶界发生迁移;如果ρ≤ε,则表示该网格点的新取向是不可以被接受的,也就是此网格点会继续保持原来的取向。

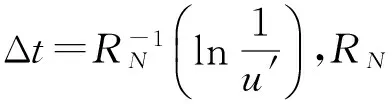
(5) 返回步骤(2)。

1.3格点能量计算的传统方法及其改进

传统kMC方法中计算格点能量公式如下:

本系统设计了左右两个测试子系统进行交替测试。一个测试，一个准备，以保证整个测试过程中测试时间的0等待。测试流程包括以下四个测试子过程：1.装置在放置区和测试区之间进出的自动控制，2.是装置硬件接点的自动检测；3.是针对非数字化装置进行的交流头精度自动校准及标签的自动打印；4.左右测试子系统的自动切换。整机测试流程的智能控制意在解决以上四个过程的自动控制问题，见图4。

(6)

其中:γ(θij)表示在格点间随着取向差θij变化的单位面积的能量，γ(θij)计算采用Read-Shockley公式，即公式(2);δSiSj表示Kronecker函数;n为近邻的网格点数。

目前已有的改进kMC中比较典型的方法是Mallick[11]提出的将Read-Shockly中大角度计算进行标准化扩展,扩展公式如下:

(7)

其中:r为常数,取0.618;Δθ为取向差。图1示出了采用传统和扩展的kMC计算得到的大角度晶界能。传统kMC中大角度晶界能设置为常数,而扩展的kMC大角度晶界能随取向差的增大而逐渐增大。但是扩展的kMC中,当取向差角度大于20°时,晶界能成为固定值,这与实际情况不符合。

图1　扩展Read-Shockley公式拟合大角度晶界能Fig.1　Extended Read-Shockley formula fitting energy in large angle grain boundary

为了进一步模拟真实的晶粒形貌的演化,本文将格点分为晶界区和非晶界区,并将势函数引入到晶界区格点能量计算。考虑到不同取向的晶粒之间存在不同能量,用该格点能量代替传统的计算结果实现模拟。由于只在晶界区引入势函数,所以减少了计算量。

2　晶粒生长的双区域kMC模拟方法

2.1现有kMC计算晶界区格点能量的缺点

在各向同性模拟中,晶界区格点能量可视为相同的值;在各向异性模拟中,则必须将其设为不同值,即将晶界分为大角度和小角度两种晶界。而当Read-Shockley公式用于各向异性的计算时,由于其只适用于小角度晶界的计算,对于大角度的计算结果会出现偏差[16],因此会导致最终的模拟生长过程偏离预测值。本文在原有方法中将势函数加入晶界区格点能量计算中,重新计算得到取向数的转换概率,避免使用Read-Shockley公式。

晶粒的长大依赖于晶界区提供的驱动力。引入势函数计算时,需要对每个格点分别进行计算,增加了计算量,因此本文只在晶界区引入势函数进行计算。

2.2模拟晶粒生长的双区域kMC方法

2.2.1概述双区域kMC方法主要分为非晶界区和晶界区,分别计算各自的取向数。在晶界区域中引入势函数,通过计算格点能量引入到取向数转换概率的计算中,优点是不用区别大、小角度晶界,而且可以对不同类型的晶界使用合适的势函数,以此来弥补传统方法的不足。由于kMC格点取向数的改变会影响周围取向数的变化,因此两区域kMC能够较好地连接。

2.2.2非晶界区域和晶界区域的划分如图2所示,整个区域的划分依据是势函数的截断半径。由于采用的是Lennard-Jones势函数,所以将距离交界线的两个格点的长度作为晶界区域,其余为非晶界区域。图中三角形表示晶界区域,椭圆表示非晶界区域,不同的颜色表示界线两侧不同取向数的晶粒。

图2　区域划分示意图Fig.2　Schematic diagram of regional division

划分晶界区域的大小对生长情况和计算量存在着影响。相同模拟时间内,如果晶界区扩大,则计算量增大,但是晶粒平均尺寸相同,原因是超过截断半径的晶粒之间无法相互影响;相同模拟时间内,如果晶界区缩小,则计算量减小,但是晶粒平均尺寸减小,原因是驱动晶粒生长的晶界能减小。

2.2.3非晶界区域的计算非晶界区域的生长方法如上述传统kMC算法所示,对非晶界区域的格点随机赋予取向数,再通过计算格点的转换概率来判断是否产生新的取向。

2.2.4晶界区域的计算多晶材料是由许多取向不同的单晶组成的,不同种取向之间的区域称为晶界区。由于同种取向间的作用力小于不同种取向间作用力,因此在晶界区就有取向不同而产生的力,称为取向力。采用势函数直接计算取向力,然后再求晶界区格点能量。势函数选用Lennard-Jones势函数,LJ势函数方法简单、计算量小,公式如下:

(8)

其中:ε表示两个原子间相互吸引作用的强弱;σ为作用势等于0时原子间的距离。

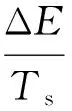
(9)

模拟温度的计算公式如下：

(10)

其中:s为取向力;v=s×d距离,d距离表示力方向的移动距离。

格点取向数的转换概率计算公式如下：

(11)

最后再通过计算得到的取向数的转换概率判断得到格点取向。

2.2.5非晶界区域和晶界区域的连接kMC方法中的取向数是向二维网格中八边形的点阵赋予一个整数值(如图3所示)。

在系统的取向数变化过程中,当相邻格点间取向一致时,则式(9)中的δSiSj为0,不一致时则为1。因此kMC方法中的每个格点取向数的计算会影响到其周围邻居点的取向数的变化,即晶界区域取向数的改变会导致非晶界区域的变化。

图3　模拟体系中四边形点阵Fig.3　Quadrilateral lattice in simulation system

在双区域kMC方法中,通过只在晶界区中引入势函数计算得到晶界区格点能量,然后通过取向数的计算将两区域较好地连接,避免了由Read-Shockley公式引起的不足,模拟结果也更符合理论规则。

3　实验分析

3.1实验设置

实验模拟采用spparks开源软件[12]实现了一个原型系统来模拟晶粒生长。参数设置为50×50网格,格点取向数为180种,势函数采用LJ势函数。

3.2各向异性对晶粒长大特征的影响

3.2.1组织演变图4所示为晶粒的组织结构随模拟时间的演化图,采用了各向异性条件。图中不同类型的晶粒用不同的颜色表示。可以看出,在各向异性条件下,组织中晶粒尺寸趋于非均匀,形状趋于不规则晶粒,说明各向异性阻碍晶粒长大,降低组织均匀化程度。

图4　各向异性条件下双区域kMC模拟的晶粒 生长微观组织演变Fig.4　Microstructures evolution in anisotropic grain growth with bi-region kMC

3.2.2晶粒尺寸分布平均晶粒尺寸的测量是在模拟二维图中随机布置3条平行于边界的直线(横向或纵向),计算每条直线上的晶粒平均截距(覆盖在一个晶粒上的测量线段的长度称为截距),取算术平均值作为晶粒平均直径[17]。其中,晶粒平均截距=长度/截到的晶粒个数。

本文随机选取纵向的3条直线,统计直线所截的晶粒尺寸和平均尺寸,并计算算术平均值。

图5示出了最大晶粒直径与晶粒平均直径的比值Db/Dm,MCS表示蒙特卡洛时间步长。图中显示,Db/Dm比值大于2.5,但小于4。以上模拟结果符合各向异性条件下的正常晶粒长大特征,与文献[18]相符。

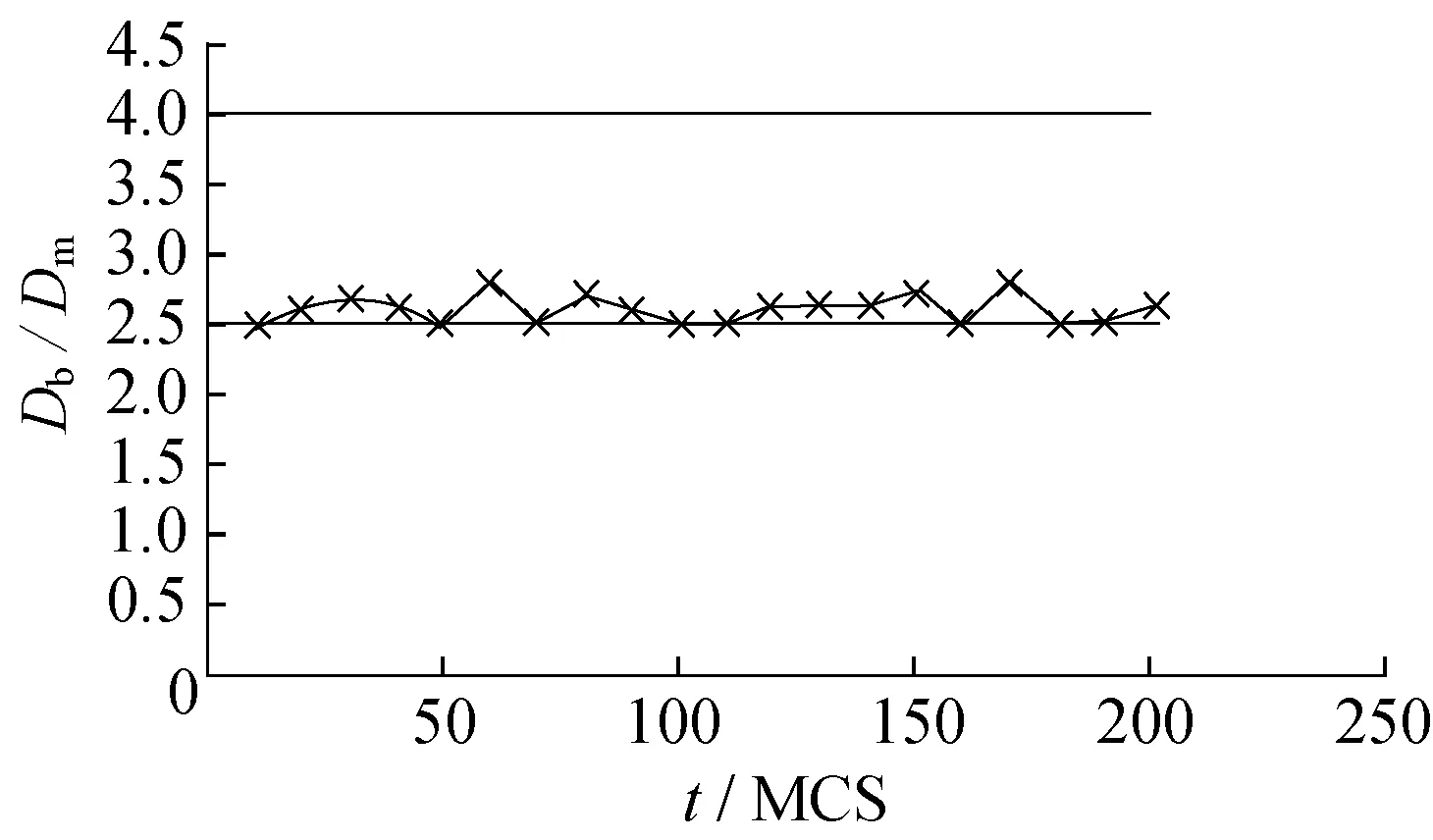
图5　最大晶粒尺寸与平均尺寸比值Fig.5　Maximum grain size and average size ratio

3.3双区域kMC与传统kMC的对比

图6示出了不同晶界夹角情况下,由Read-Shockley公式计算得到的晶界区能量变化过程。可以看出,虽然变化趋势基本符合要求,但是对于大角度晶界(即夹角大于15°)不符合实际情况[19]。从图中也发现,生长过程中大角度晶界所占的数量多于小角度晶界。

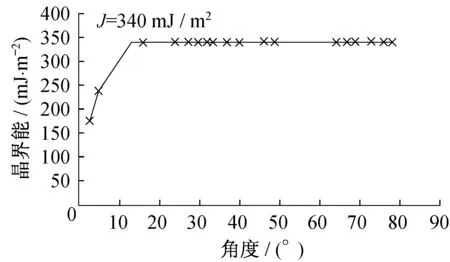
图6　Read-Shockley公式拟合晶界区格点能量Fig.6　Read-Shockley formula fitting energy in grain boundary

图7、图8分别示出了传统动力学蒙特卡洛和双区域动力学蒙特卡洛的模拟结果。将两种kMC方法对比发现,采用双区域kMC的模拟方法得到的模拟结果更加接近理论值。

图7　传统动力学蒙特卡洛模拟结果Fig.7　Simulation results of traditional kinetic Monte Carlo

图8　双区域动力学蒙特卡洛模拟结果Fig.8　Simulation results of double-region kinetic Monte Carlo

晶粒生长过程中主要有两种拓扑演化机制:小于六边形晶粒的消失和近邻切换机制。计算晶粒的边数可以通过计算其周围不同晶粒的种类获得。

3.4双区域kMC与改进kMC的对比

本文选取改进kMC中比较典型的扩展Read-Shockly方法[11]与双区域kMC方法做实验比较。通过图9和图10可以发现双区域方法比改进kMC更接近理论值。

图9　近邻转换机制Fig.9　Nearest neighbor conversion mechanism

图9展示的是用双区域kMC模拟的近邻转换机制,而用改进的kMC无法得到该结果。近邻转换机制指的是由于在晶粒生长过程中,晶界能量会不断减小,因此相邻的两个晶粒交接处的晶界会消失。如图9中,4和5这两个相邻的晶粒之间的交界线消失。

图10示出了晶粒生长指数比较结果。从图中可以看出，改进的kMC的晶粒生长指数超过了0.51,超过了理论最大值(晶粒长大指数n与Hillert[15]指数的关系n=1/m,根据统计方法,理论最大值n=0.5),而双区域kMC符合各向异性的晶粒生长指数的变化规律,即小于各向同性条件下的生长速度,也远小于最大理论值。

图10　晶粒生长指数Fig.10　Grain growth exponent

4　结束语

本文介绍了利用双区域动力学蒙特卡洛方法对各向异性的晶粒生长进行模拟,解决了传统蒙特卡洛模拟只适用于计算小角度晶界的限制。该方法将势函数通过计算格点能量引入取向数的转换概率计算中,并采用分区域方法减少计算量。双区域动力学蒙特卡洛方法与已有的传统动力学蒙特卡洛方法和改进的动力学蒙特卡洛方法的模拟结果相比,在相同的模拟时间内,双区域方法的微观组织演变更符合晶粒生长特征,晶粒生长指数也更接近理论值。

[1]FAN D,CHEN L Q.Computer simulation of grain growth using a continuum field model[J].Acta Materialia,1997,45(2):611-622.

[2]YU Q,NOSONOVSKY M,ESCHE S K.On the accuracy of Monte Carlo Potts models for grain growth[J].Journal of Computational Methods in Sciences & Engineering,2008,8(4/6):227-243.

[3]FU K,FU Y.Kinetic Monte Carlo study of metal organic chemical vapor deposition growth mechanism of GaSb quantum dots[J].Applied Physics Letters,2008,93(10):101906-10190-3.

[4]ANDERSON M P,SROLOVITZ D J,GREST G S,etal.Computer simulation of grain growth：I.Kinetics[J].Acta Met allurgica,1984,32(5):783-791.

[5]PATTERSON B R,ROWENHORST D J,TIKARE V,etal.Affinities for topological arrangements in grain structures[J].Acta Materialia,2014,79(30):411-420.

[6]HOLM E A,HASSOLD G N,MIODOWNIK M A.On misorientation distribution evolution during anisotropic grain growth[J].Acta Materialia,2001,49(15):2981-2991.

[7]ROHRER G S.Influence of interface anisotropy on grain growth and coarsening[J].Annual Review of Materials Research,2005,35(1):

[8]YU Q,ESCHE S K.Modeling of grain growth kinetics with Read-Shockley grain boundary energy by a modified Monte Carlo algorithm[J].Materials Letters,2002,56:47-52.

[9]BATTAILE C C.The kinetic Monte Carlo method:Foundation,implementation,and application[J].Computer Methods in Applied Mechanics & Engineering,2008,197:3386-3398.

[10]张继祥,关小军.异常晶粒长大的Monte Carlo模拟[J].中国有色金属学报,2006,16(10):1689-1697.

[11]MALLICK A,VEDANTAM S.Phase field study of the effect of grain boundary energy anisotropy on grain growth[J].Computational Materials Science,2009,46(1):21-25.

[12]HILLERT M.On the theory of normal and abnormal grain growth[J].Acta Met Allurgica,1965,13(3):227-238.

[13]GOTTSTEIN G,SHVINDLERMAN L S,GOTTSTEIN G,etal.Grain boundary migration in metals:Thermodynamics,kinetics,applications[J].Journal of Engineering Mechanics,1998,126:888.

[14]GREST G S,SROLOVITZ D J,ANDERSON M P.Computer simulation of grain growth：Ⅳ.Anisotropic grain boundary energies[J].Acta Met allurgica,1985,33(85):509-520.

[15]BORTZ A B,KALOS M H,LEBOWITZ J L.A new algorithm for Monte Carlo simulation of king spin systems[J].Journal of Computational Physics,1975,17:10-18.

[16]GRUBER J,MILLER H M,HOFFMANN T D,etal.Misorientation texture development during grain growth：Part Ⅰ.Simulation and experiment[J].Acta Materialia,2009,57(20):6102-6112.

[17]RADHAKRISHNAN B,ZACHARIA T.Simulation of curvature-driven grain growth by using a modified monte carlo algorithm[J].Met allurgical & Materials Transactions A,1995,26(1):167-180.

[18]张继祥,关小军,孙胜，等.晶粒长大过程微观组织演变Monte Carlo方法模拟[J].山东大学学报(工学版),2005,35(4):1-5.

[19]OLMSTED D L,FOILES S M,HOLM E A.Survey of computed grain boundary properties in face-centered cubic metals:I.Grain boundary energy[J].Acta Materialia,2009,57(13):3694-3703.

[20]MULLINS W W.Two-dimensional motion of idealized grain boundaries[J].J Appl Phys,1956,27:900-904.

Bi-region Kinetic Monte Carlo Simulation of Grain Growth

ZHANG Ping,LI Jian-hua,LI Hong-lin

(School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China)

There exist deviations between the results of most kinetic Monte Carlo (kMC) simulation of grain growth and the theoretical value of grain growth.An important reason is that the Read-Shockley formulation in most kMC simulation is only suitable for the computation of small-angle grain boundary.Aiming at this problem,a bi-region kMC method is proposed in this paper,which handles both situation of small-angle grain boundary and large-angle grain boundary.In the proposed method,the transition probability of orientation number is obtained using lattice energy based on potential functions,not using Read-Shockley formula.In order to solve the large computational problem caused by introducing potential functions,kMC single-region structure of traditional dynamics is divided into two regions:the one without grain boundary and the one with the grain boundary.Due to potential function computation only used in the region of grain boundary,the computing time is reduced.Experiment results show that the micro-structure evolution of bi-region kMC method is more consistent with the feature of grain growth than that of existing traditional and improved kMC,and the grain growth exponent is closer to the theoretical value than that of existing kMC.

kMC; grain growth; micro-structure; grain growth exponent

A

1006-3080(2016)03-0387-06

10.14135/j.cnki.1006-3080.2016.03.015

2015-09-25

张平(1991-),男,江苏常州人,硕士生,研究方向为计算机辅助设计。E-mail:zhangping_1@foxmail.com

通信联系人：李建华,E-mail:jhli@ecust.edu.cn

TP391