一种基于蚁群思想的动态路径寻优算法的实现及仿真

周秀娟，花　嵘，史　娟，高玉励

(1.山东科技大学 信息科学与工程学院 山东 青岛 266590；2.青岛黄海学院 山东 青岛 266427)



一种基于蚁群思想的动态路径寻优算法的实现及仿真

周秀娟1，花嵘1，史娟1，高玉励2

(1.山东科技大学 信息科学与工程学院 山东 青岛 266590；2.青岛黄海学院 山东 青岛 266427)

摘要：为了提高路径寻优算法的效率和实时性，本文实现了一种名为DPO-AC的基于蚁群思想的动态路径寻优算法(the ant colony algorithm with dynamic path optimization)，在改进蚁群算法的基础上结合神经网络的实时预测方法和限定区域的搜索方式，解决算法在大型网络路径寻优时实时性差、收敛慢的问题。仿真实验表明DL-ACO算法有比较好的稳定性、收敛性和实时性。

关键词：路径寻优；算法；蚁群；限定区域；阻塞矩阵

随着城市人口的不断增加，城市交通路网趋于大型化、复杂化，且随着人均车辆保有量的快速增长，城市交通情况日渐复杂化。传统的路径寻优算法[1-3]不考虑路网的动态变化情况，把路网的拓扑性作为唯一依据，不考虑起点和终点的位置、方向，虽简单易用，但效率偏低。近年来，随着人工智能的发展，智能算法被越来越多的用于解决大规模、非线性、全局最优的复杂问题，将其应用于路径寻优问题求解已成为城市交通研究的一个热点。张学敏[4]在蚁群算法中引入了方向引导信息来提高城市路网求解的收敛速度，靳凯文[5]等人在蚁群算法的基础上对信息素、启发信息的重要性和信息素的保留率进行了分阶段调整，提高了算法的稳定性。

用于交通路网路径寻优的限定区域的方法主要有两种:椭圆区域[6]和矩形区域[7]，相比于椭圆区域，矩形区域的算法搜索效率更高[7]。BP神经网络[8]虽然能够准确、有效的实现道路交通信息的实时预测，但也存在以下缺陷：因采用梯度下降法进行搜索，而梯度下降法固有的特点使得易形成局部极小值[9]，学习率较低使得训练时间较长，而且BP神经网络的隐层节点数目选取缺乏理论基础。

本文为满足大型路网路径寻优的需要，结合交通网的动态特性，从避免局部最优的角度出发，对蚁群算法中的选择策略进行了改进，并将限定区域和动态阻塞矩阵应用到蚁群算法中，设计了一种名为DPO-AC的基于蚁群思想的动态路径寻优方法。

1经典蚁群算法及存在问题分析

经典的蚁群算法是20世纪90年代Dorigo M[10]等人受蚂蚁觅食行为启发提出的一种模拟进化算法，以人工蚂蚁模拟自然蚂蚁求解优化组合问题。经典的蚁群路径寻优算法模型表述为：m只蚂蚁从起点S出发,路网所有路段(i，j)的信息素浓度τij(t)在初始时刻为相同常量，启发信息ηij(t)设为路段距离dij的倒数，在t时刻蚂蚁k在路网交叉口(路网节点)i选择下一节点j的概率表示为[11]：

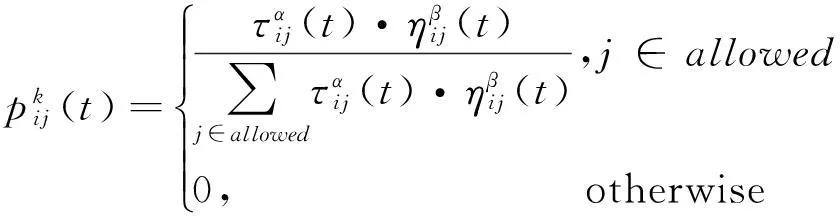
(1)

其中，α和β分别表示信息素和启发信息的重要性。

经过n个时刻，蚂蚁从起点到达终点后对路段残余信息素进行更新，参数ρ(0≤ρ≤1)表示信息素的保留率，各路段上的信息素按式(2)进行更新。

τij(t+n)=ρ·τij(t)+Δτij(t)。

(2)

Δτij(t)表示t时刻(i，j)路段残存的信息素浓度。

根据更新策略的不同，Dorigo M提出了三种蚁群算法模型，蚁周模型、蚁量模型、蚁密模型，三者的区别在于：后两种用的是局部信息，第一种用的是全局信息，故性能最佳。

蚁周模型公式如下：

(3)

其中，Q是一个常量表示信息素强度，L表示蚂蚁本次循环经过路径的长度。当所有蚂蚁完成一次循环，记录最优路径，重复上面的过程，直到预设结束条件满足。

蚁群算法具有很好的路径寻优能力，但是在实际的路径寻优中还存在着如下问题：1)在经典蚁群算法中没有方向引导，面对大型网路时容易出现“之”字搜索结果，影响搜索速度；2)公式1的概率函数缺乏对动态因素的考虑；3)因算法在搜索时的概率性和正反馈作用，容易出现局部最优。

2DPO-AC算法思想

蚁群算法从结构上分为数据预处理和算法迭代两部分。本文的DPO-AC算法主要从以下两个方面对蚁群算法进行了改进：在数据预处理部分，通过设定算法的搜索区域和采用改进的BP神经网络来实时确定动态阻塞因子；在算法迭代中，改进了选择概率和选择策略，并通过改进算法的启发信息矩阵来确定算法的搜索方向，以防止算法出现局部最优。

2.1 数据预处理部分改进

给定起点S(xs,ys)和终点V(xv,yv)，最短路径的极限值ESV(欧式距离)即为定值，采用延长SV的方法得到椭圆长轴MD(如图1)。延长系数可以用样本分析的方法，确定最短距离Pab和欧式距离Eab的比值系数f，把f作为SV的延长系数。椭圆长轴计算公式为：

MD=f×Esv。

(4)

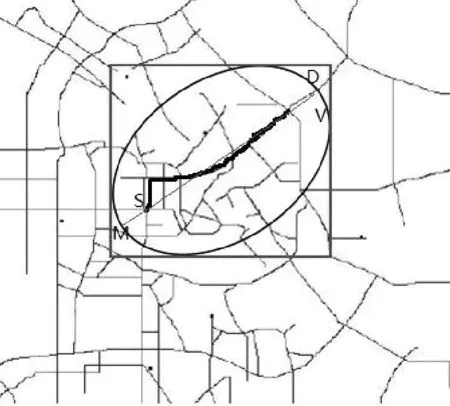
图1　 限定区域的选定

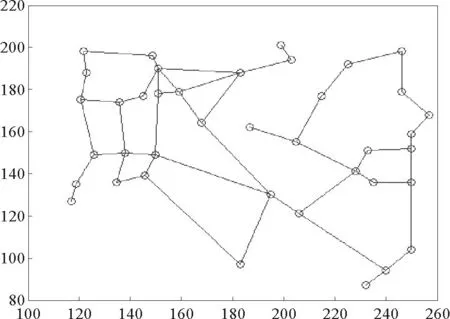
图2　矩形区域内路网简略图

利用长轴MD的值求解椭圆方程

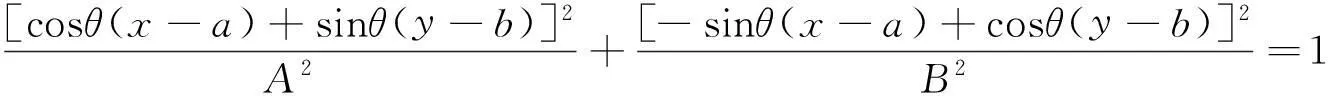
(5)

得到的最值即为矩形区域的边界值：

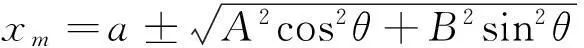
(6)

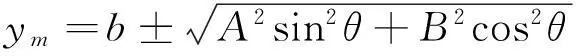
(7)

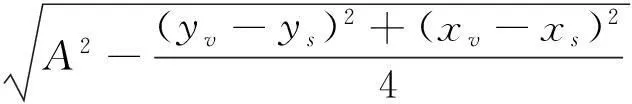
针对BP神经网络存在的缺陷，本文采用自适应调节法根据输出误差大小自动调整学习率，当连续两次权值迭代中梯度下降方向相同，则表明梯度下降的速度过慢，此时应该增加学习率，学习率乘以增量因子kin；当连续两次权值迭代中梯度下降方向相反，则表明梯度下降的速度过快，需要减小学习率，学习率乘以减量因子kde。

权值的调节公式为：

(8)

自适应调节方法可以提高算法的学习速度，但是容易出现波动导致局部最优，本文采用附加动量法来避免此问题。具体公式为：

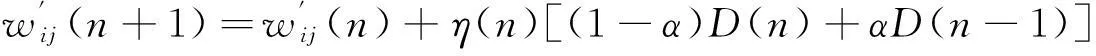
(9)

其中：α表示动量因子，一般取值介于0和1之间。

针对BP神经网络的隐层节点数目选取缺乏理论基础的问题，本文采用多值对比的方法确定隐层节点数。根据隐层节点的经验公式：

(10)

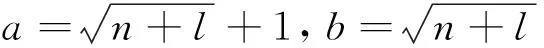
2.2算法迭代部分改进分析

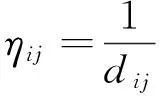
为了提高蚁群算法对动态路网的适应性，在经典蚁群算法选择概率(公式(1))的基础上加入改进的BP神经网络算法得到的路网动态因子，得到新的概率选择公式如下：

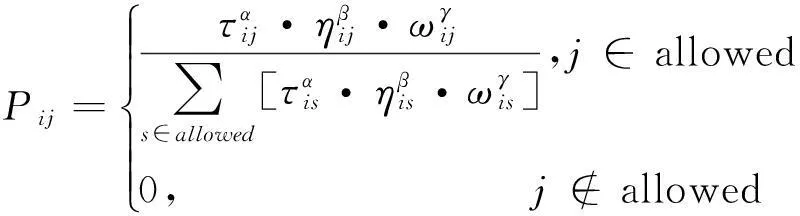
(11)

其中，Pij表示i到j的概率，τij表示i到j路段的信息素浓度，ηij表示i到j路段的距离的倒数，ωij表示i到j路段的阻塞值，α，β，γ为各参数的比重。

针对由于蚂蚁寻找路径的随机性而带来的易出现局部最优的问题，本文依据2-8定律，提出采用2-8分批方式对蚁群算法的选择策略进行改进。

2指的是前20%的蚂蚁采用最大概率方法选择下一节点，公式为

j=max(Pallowed)，

(12)

其中：Pallowed=(pi1,pi2,…,pin)，表示可选下一节点的概率集合；

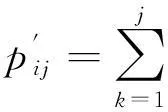
3DPO-AC算法设计及分析

针对上面的改进方案，本节设计了DPO-AC算法，伪代码如下：

Procedure DPO-AC

Input:NC_Max,C,R,S,V‘NC_Max是最大迭代次数；C是路网节点；R是初始信息素矩阵；S是起点；V是终点。

New_C=call Relimited(C);‘矩形限定区域法得到新的数据集

W=call BPNetwork(Q);‘BP神经网络求解动态阻塞矩阵

for each edge

set initial pheromone valuePhe0

end for

Whileinot more thanNC_Max

for each antk

set it toS

if the visited node is notV

20% of ant choose next node by maxPij,80% of ant choose next node by roulette wheel selection

end if

end for

Compute the lengthCkof the tour constructed by thekthant

for each edge

Update the pheromone value

end for

end while

print result

end procedure

4DPO-AC算法仿真测试及分析

4.1测试方案

以天津市的交通路网为例，该路网有124个节点，以出行时间最短为目标求解最优路径。

1)确定矩形搜索区域，产生起点和终点，对天津市的路网采样统计确定比例系数f=1.96,由前面提到的求解方法确定矩形区域内的节点，运行代码得到矩形区域的节点数为39。图2是矩形区域内路网的MATLAB简略图(图2只表示各节点的位置关系，并不是实际位置)。

2)通过BP神经网络得到各个路段的阻塞矩阵，取i-1，i-2，i-3，i-4，i-5，i-6，i-7，i-8，i-9，i-10，以10个时间段(每个时间段5 min)各路段的交通流量为输入，i时刻的交通流量为输出，参照MATLAB神经网络工具箱增量因子kin默认值取1.05，减量因子kde默认值取0.7，动量因子α默认值取0.9。隐层取4个节点，经预测值计算t时刻39×39的阻塞矩阵，结果如下：

其中，阻塞等级分为5级(0.2,0.4,0.6,0.8,1)，值越大说明该路段畅通性越好，0表示对角元素或不连通。

3)采用DPO-AC算法求解t时刻路网两节点的最优路径，根据文献[12]，参数设定为：信息启发因子为1；期望因子为5，信息强度为100；蚂蚁数目为50；最大迭代次数为50；期望矩阵是距离的倒数；矩形内40节点的信息素矩阵为：

4.2测试结果

首先测试算法的正确性。将本文算法中的动态阻塞因子ω设为定值，即每个路段的阻塞程度相同，求出s到v的静态最短路径，并与Dijkstra算法求出的静态最优路径进行对比，结果如图3，可看到两路径完全重合，为3-6-7-12-19-34-35，验证了本文算法的正确性。

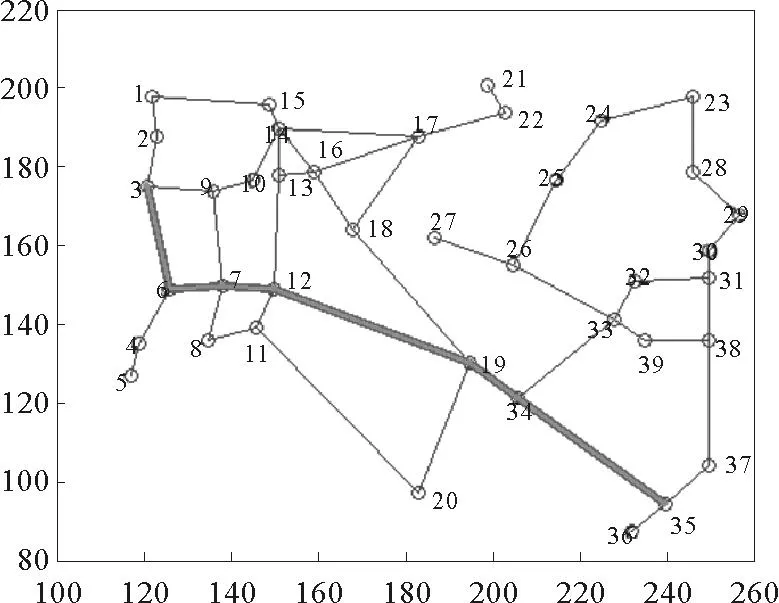
图3　Dijkstra算法与DPO-AC算法静态最短路径

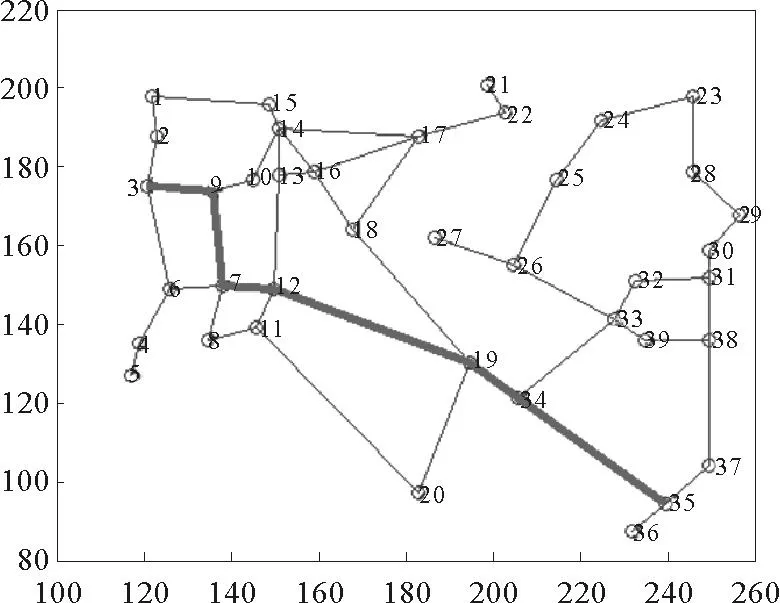
图4　DPO-AC算法求解的动态最优路径

其次仿真验证本文算法的动态性。在MATLAB下对DPO-AC算法中的动态阻塞因子进行了调整，具体是增大3-6路段的阻塞因子，DPO-AC算法避开了该阻塞路段，求得的动态最优路径为：3-10-7-12-19-34-35(如图4)。

然后验证算法的实时性。如图5是某日晚高峰时的搜狗地图交通实况信息，从A点到C点的静态最短路径为线路1(A-B-C路段)。实时路况信息显示，当前时刻线路1的B-C段出现了车速缓慢和拥堵的情况，DPO-AC算法选择了各路段均为畅通状态的线路2(A-D-C路段)为当前实时最优路径。

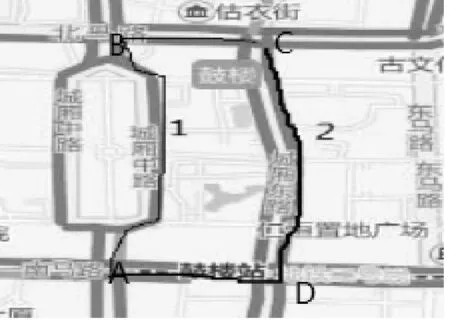
图5　晚高峰实时路况

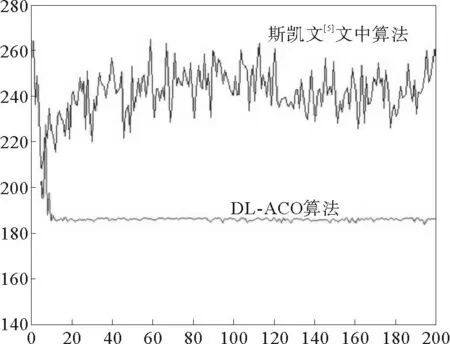
图6　两种算法的迭代次数和平均最短路径对比图

最后验证算法的稳定性和收敛速度。在相同的数据集和蚂蚁数量(测试中为50只)前提下，将本文的DPO-AC算法与靳凯文[5]算法从迭代次数和平均最短路径两方面进行了对比。由于DPO-AC算法采用了分批的选择策略并指定搜索方向，仅需迭代15次结果就已经趋于稳定，靳凯文算法却一直处于浮动状态(见图6)，这说明DPO-AC算法的稳定性比较好。从达到收敛状态所用时长来看，Dijkstra算法为20.103s，靳凯文算法迭代100次的时间为31.002s，DPO-AC算法迭代15次的时间为10.672s，可以看出DPO-AC算法在收敛速度上也具有较大优势。

综上，相对于经典的路径寻优方法来说，DPO-AC算法有很明显的灵活性，适应现代交通中存在的不确定因素；与以往的蚁群算法相比，所需要的蚂蚁数和迭代次数都很小，收敛速度更快。

4结语

本文分析了现有蚁群算法在求解动态路网最优路径中存在的问题，并针对其中存在的局部最优、缺乏动态因子以及搜索速度慢的问题做了相应的改进。测试结果表明DPO-AC算法在保证正确性的前提下，收敛速度和稳定性上有较大提高。但是本文还存在一定的不足，比如限定区域的延长比值不够精确，BP神经网络的时间间隔有待缩小。

参考文献：

[1]付梦印,李杰,邓志红.限制搜索区域的距离最短路径规划算法[J].北京理工大学学报,2004,24(10):881-884.

FU Mengyin,LI Jie,DENG Zhihong.Route planning algorithm for the shortest sistance within a restricted searching area[J].Transactions of Beijing Institute of Technology,2004,24(10):881-884.

[2]李晶,闫军.基于Dijkstra算法和Floyd算法的物流运输最短路径研究[J].科技信息,2012,34:575-576.

LI Jing,YAN Jun.Shortest path of logistics transportation based on based on Dijkstra algorithm and Floyd algorithm[J]. Science and Technology Information,2012,34:575-576.

[3]张伟,张秋菊.Dijkstra算法在AGV调度系统中的应用[J].机械设计与制造工程,2015,44(5):61-64.

ZHANG Wei,ZHANG Qiuju.Application of Dijkstra algorithm in AGV scheduling system[J].Mechanical Design and Manufacturing Engineering,2015,44(5):61-64.

[4]张学敏,张航.基于改进蚁群算法的最短路径问题研究[J].自动化技术与应用,2009,28(6):4-7.

ZHANG Xuemin,ZHANG Hang.Research on shortest path problem based on improved ant colony algorithm[J].Automation Technology and Application,2009,28(6):4-7.

[5]靳凯文,李春葆,秦前清.基于蚁群算法的最短路径搜索方法研究[J].公路交通科技,2006,23(3):128-130.

JIN Kaiwen,LI Chunbao,QIN Qianqing.Study on shortest path search method based on ant colony algorithm[J].Technology of Highway and Transport,2006,23(3):128-130.

[6]STIG N,BENGT R.Computer cartography shortest route program[M].Lund:The Royal University of Lund,1969.

[7]陆锋,卢冬梅,崔伟宏.交通网络限制搜索区域时间最短路径算法[J].中国图象图形学报,1999,4(10):849-853.

LU Feng,LU Dongmei,CUI Weihong.The traffic network searching region limited time shortest path algorithm[J].Journal of Image and Graphics,1999,4(10):849-853.

[8]葛哲学,孙志强.神经网络理论与MATLABR2007实现[M].北京:电子工业出版社,2007:111.

[9]高慧,赵建玉,贾磊.短时交通流预测方法综述[J].济南大学学报(自然科学版),2008,22(l):88-94.

GAO Hui,ZHAO Jianyu,JIA Lei.A review of short term traffic flow forecasting methods[J].Journal of University of Jinan (Science and Technology),2008,22(l):88-94.

[10]COLORM A,DORIGO M,MINIEZZO V.Distributed optimization by ant colonies[C]//Proceedings of the First European Conference on Artificial Life.Paris,France:Elsevier Publishing,1991:134-142 .

[11]杨兆升.城市交通流诱导系统理论与模型[M].北京:人民交通出版社,2000.

[12]张可,凌海峰.基于均匀设计和混沌理论的蚁群算法参数调整[J].计算机工程,2012,38(14):141-143.

ZHANG Ke,LING Haifeng.Parameter turning of ant colony algorithm based on uniform design and chaos theory[J].Computer Engineering,2012,38(14):141-143.

(责任编辑：李磊)

收稿日期：2016-03-25

基金项目：山东省科技发展计划项目(13GGX10118);青岛经济技术开发区重点科技发展计划项目(2013-1-65)

作者简介：周秀娟(1990—)，女，山东聊城人，硕士研究生，主要从事智能交通研究. E-mail:hrfy@263.net

中图分类号：TP391.9

文献标志码：A

文章编号：1672-3767(2016)04-0114-07

Implementation and Simulation of a Dynamic Path Optimization Algorithm Based on Ant Colony Thoughts

ZHOU Xiujuan1,HUA Rong1,SHI Juan1,GAO Yuli2

(1.College of Information Science and Engineering,Shandong University of Science and Technology,Qingdao,Shandong 266590,China ;2.Qingdao Huanghai College,Qingdao,Shandong 266590,China )

Abstract:In order to improve the efficiency and instantaneity of path optimization algorithms,a dynamic path optimization algorithm named the ant colony algorithm with dynamic path optimization(DPO-AC) was proposed.On the basis of the improved ant colony algorithm and combined with neural network real-time prediction and limited area search,the proposed algorithm solved the problem of poor real-time performance and slow convergence of large network path optimization algorithms.Simulation results show that DL-ACO has better stability,convergence and instantaneity.

Key words:path optimization;algorithm;ant colony;limited area;block matrix

花嵘(1969—)，男，江苏常州人，副教授，博士，主要从事高性能计算、多智能体等方面的研究，为本文通作者.