基于增广拉格朗日交替方向法的矩阵秩最小化算法研究

陈勇勇，王永丽，于慧慧

(山东科技大学 数学与系统科学学院，山东 青岛 266590)



基于增广拉格朗日交替方向法的矩阵秩最小化算法研究

陈勇勇，王永丽，于慧慧

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

摘要：针对含有较大奇异值的矩阵秩最小化问题，采用对数行列式函数代替核范数作为秩函数的非凸近似，应用增广拉格朗日交替方向法求解矩阵秩最小化问题。当罚参数β>1时，证明此算法产生的迭代序列收敛到原问题的稳定点。最后利用实际数据和随机数据，通过数值实验验证所提出的算法较现有的求解核范数矩阵秩最小化问题的算法更高效。

关键词：对数行列式函数；核范数；增广拉格朗日交替方向法；低秩矩阵表示

1引言

考虑矩阵秩最小化问题

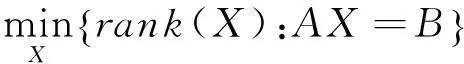
(1)

其中，X∈Rm×n，A∈Rp×m,B∈Rp×n是数据矩阵。

矩阵秩最小化问题在机器学习、数据挖掘、计算机视觉、图像处理、控制、生物信息学等领域有广泛的应用，由于求解此问题是NP-hard问题，学者们往往使用核范数作为矩阵秩函数的凸近似[15 ]，即通过求解如下核范数最小化问题来得到问题(1)的近似解：

(2)

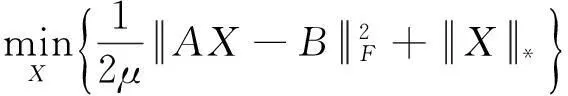
(3)

求解核范数无约束最小化问题常用的算法有加速近似梯度法(accelerated proximal gradient method with line-search,APGL)[1]、增广拉格朗日法(augmented lagrangian method， ALM)[2]、交替方向乘子法(alternating direction method of multiplier,ADMM)[3,4]、坐标下降法(coordinate descent)[5]等。当矩阵的某些奇异值较大时，彭冲等[7]求解子空间聚类问题时发现，利用对数行列式函数对矩阵秩函数进行近似的效果较好，而核范数的近似效果较差。基于此，本文用对数行列式函数代替核范数作为矩阵秩函数的近似，同时考虑到对数行列式函数的非凸性，应用增广拉格朗日交替方向法求解问题(3)，提出一个新的算法，在适当条件下证明了算法的收敛性，并通过实例验证了算法的有效性。

2对数行列式函数最小化问题

2.1问题描述

在问题(3)中，利用对数行列式函数代替核范数，可得如下形式：

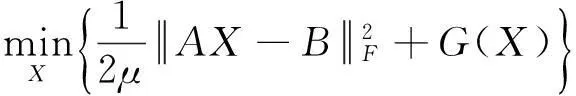
(4)

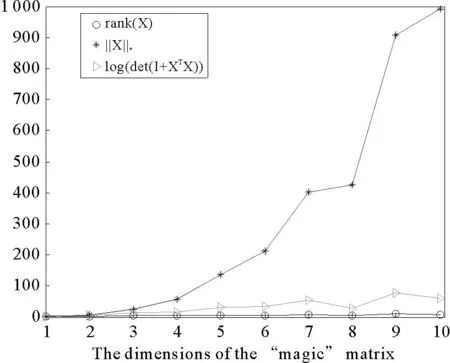
图1　核范数与对数行列式函数对“magic”矩阵秩的近似效果比较

2.2增广拉格朗日交替方向法

引入辅助变量Y∈Rm×n，将问题(4)转化成如下等价形式：

(5)

问题(5)的增广拉格朗日函数为

(6)

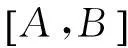
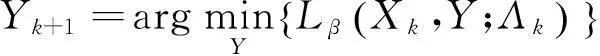
(7a)

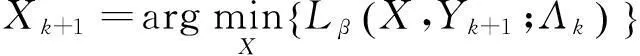
(7b)

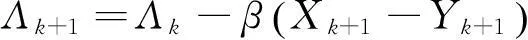
(7c)

子问题(7a)有封闭解：

(8)

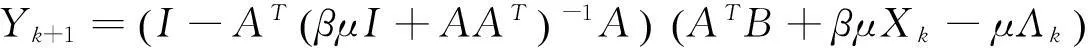
(9)

这样就可以将一个n×n的矩阵求逆转化成一个m×m的矩阵求逆。

子问题(7b)等价于

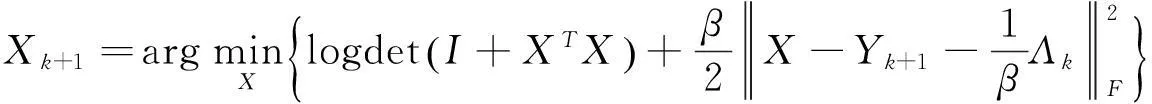
(10)

此问题同样有封闭解，下面给出求解此问题的几个定理。

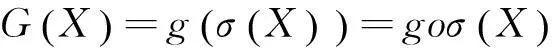
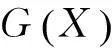
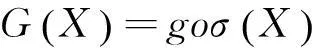
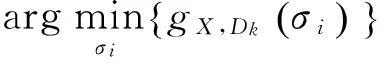
(11)

(12)

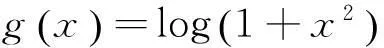
由上述结论可得本文的算法框架如下。

算法1： 求解问题(5)的增广拉格朗日交替方向法(ALADMLD)

初始化：任给矩阵X0∈Rm×n，Λ0∈Rm×n，置迭代次数k=0；

步骤1： 根据式(8)或者(9)计算Yk+1；

步骤2： 根据(10)和性质1计算Xk+1；

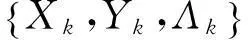
输出：X*=Xk。

备注1：算法ALADMLD步骤3中γ是为了加快算法的收敛速度。本文的实例中取γ=1.5。

3算法的收敛性分析

本节中，我们将证明本文所提出的算法收敛到原问题的稳定点。

问题(5)的KKT条件为：

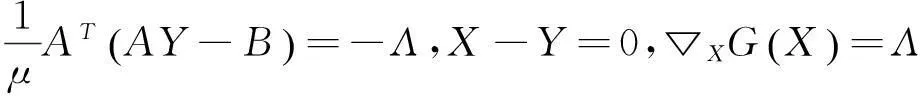
(13)

证明：子问题(7b)的最优解Xk+1必须满足一阶最优性条件

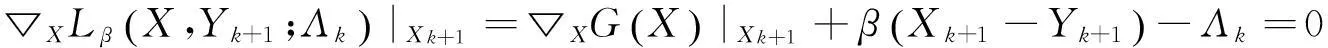
(14)

将式(7c)代入(14)式，得到：

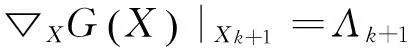
(15)

由定理1可得

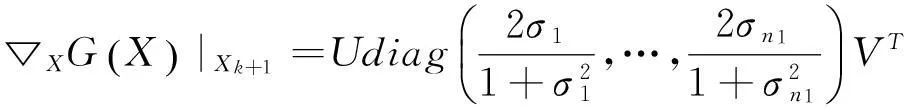
(16)

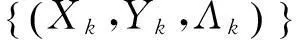
证明：1) 由增广拉格朗日函数的定义(6)及算法步骤可得

上式的最后一个等式由(7c)得出。因此

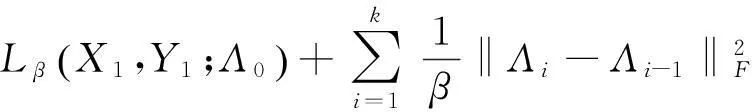
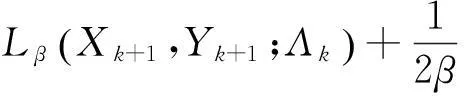
(17)

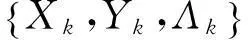
X*-Y*=0。

(18)

当k→∞，由(14),(15)式得

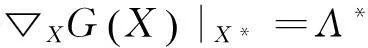
(19)

由(7a)式的一阶最优性条件，可得

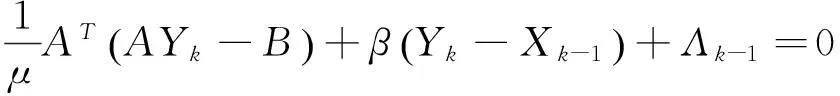
(20)

将(7c)代入(20)式得到

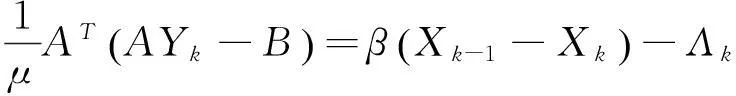
(21)

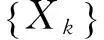
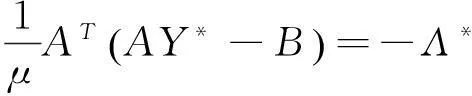
(22)

4实验结果与分析

本节对已有的求解核范数矩阵秩最小化问题的较先进的算法—APGL[1]，LADM[3]，LSA[10]，SCC[11]，LRR[12]，LRSC[13]，SSC[14]与本文提出的ALADMLD算法进行比较。需要指出的是APGL代码可以从软件包SLEP中获得。本文所有的实验都是在Windows8系统MATLABR2013a中运行的。

实验分为三类：

1) 4.1节采用实际数据(Scene和股票数据)，比较APGL与ALADMLD求解多元线性分析系数问题；

2) 4.2节采用随机数据，比较LADM与ALADMLD算法的高效性；

3) 4.3节采用ExtendedYaleB数据应用到人脸识别，比较ALADMLD算法与LSA，SCC，LRR，LRSC，SSC的有效性。

由于算法中参数比较多，首先给出实验的基本细节。

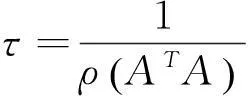
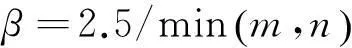
3) 参数μ。为了验证算法ALADMLD的有效性，实验采用多个μ值进行测试，如表1所示。

4) 终止准则。ALADMLD和LADM算法的终止准则：

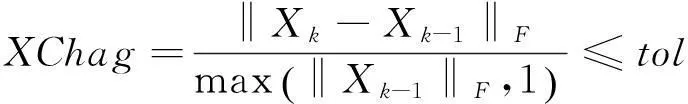
其中，tol=10-6是终止参数。实验的最大迭代次数kmax=100。

5) 评价标准。均方根误差(rootmeansquareerror，RMSE)

表1给出了所有实验数据的统计信息。

表1　实验中的数据集统计信息

4.1APGL与ALADMLD的实验结果

本小节采用两种实际数据：Scene和Stock，这些数据都可以从网上下载。为了使算法具有可比性，本实验采用的都是APGL算法使用的默认参数。图2给出了算法APGL和ALADMLD利用两种实际数据计算得出的均方根误差随迭代次数的变化。图2(a)中算法APGL和ALADMLD的迭代次数分别是100和5，图2(b)中算法APGL和ALADMLD的迭代次数分别是6和5。虽然图2(b)中的迭代次数很相近，但是就均方根误差来说，算法ALADMLD的精度比APGL高出很多。

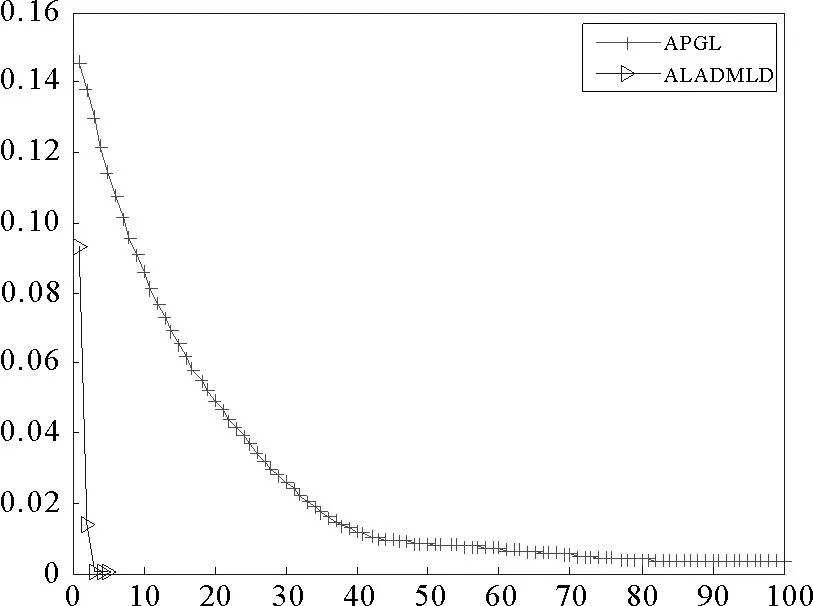
图2(a)　测试Scene数据的均方根误差

图2(b)　测试Stock数据的均方根误差

4.2LADM与ALADMLD的实验结果

因为算法LADM与ALADMLD都属于增广拉格朗日方法，故两种算法的比较更具有说服力。为了更好地验证算法的有效性，此实验采用文献[3]的方式生成数据矩阵A，具体产生过程如下：

1)sqrt_lam=sqrt(lam_max);

2) [P,～] = qr(randn(p));

3) d = [1:1 + rand(min(p,m) -2,1) * (sqrt_lam -1);sqrt_lam ];

4) [Q,～] = qr(randn(m));

5) A=P*spdiags(d,0,p,m)*Q’。

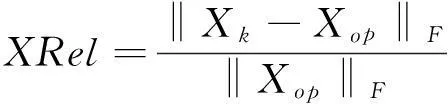
4.3LSA,SCC,LRR,SSC,LRSC与ALADMLD的实验结果

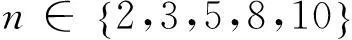
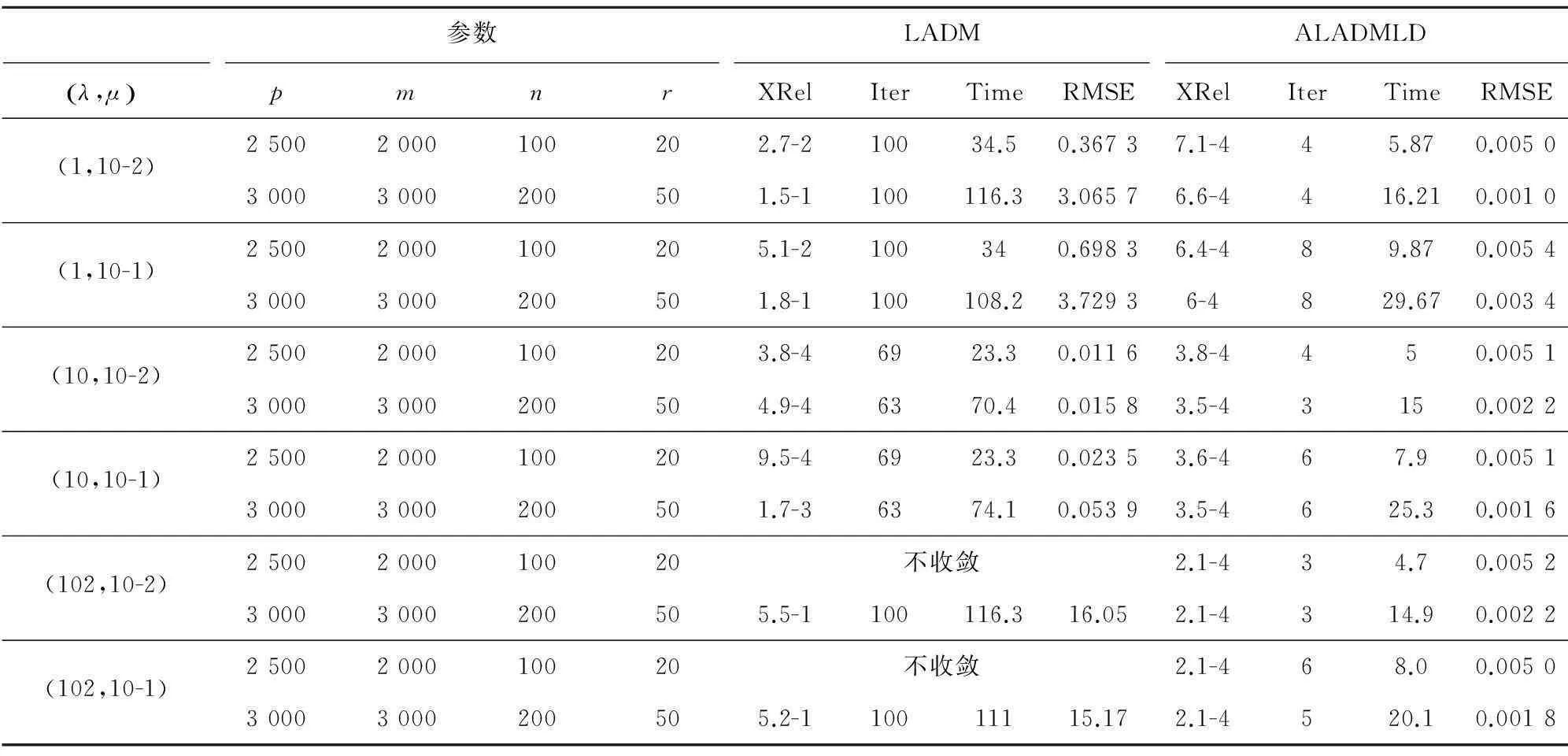
表2　算法LADM和ALADMLD的结果比较

4.4实验总结

通过实验结果的比较发现，本文提出的算法ALADMLD算法在许多方面较现有的求解核范数的有效算法—APGL和LADM更高效，具体可归结为以下几点：

1) 三种算法都属于一阶方法，即在每次迭代过程中，只需要计算函数值和梯度信息，因此三种算法都可用于求解大规模数据问题，但是当终止准则相同时，ALADMLD的计算速度更快；

2) APGL和LADM算法的有效性严格依赖于近似映射，近似参数τ的选取不容易把握；而ALADMLD算法则不需要对子问题进行近似映射，不涉及近似参数τ的选取，因此更加高效。

3) 当矩阵的某些奇异值比较大时，采用对数行列式函数近似矩阵秩函数的近似效果优于核范数的近似效果。

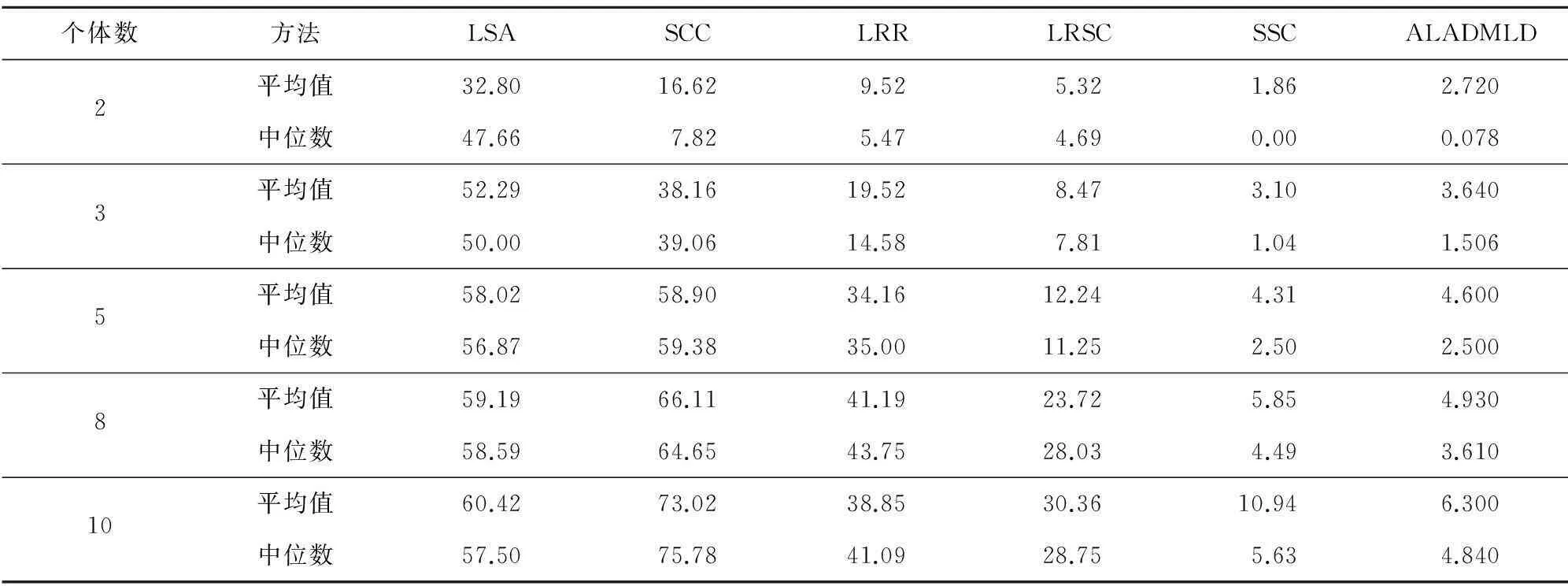
表3　应用Extended Yale B数据的聚类误差

5结论

针对矩阵秩最小化问题，提出了对数行列式函数作为矩阵秩函数的非凸近似。虽然此矩阵秩最小化问题是非凸的，通过引入辅助变量，应用增广拉格朗日交替方向法求解此矩阵秩最小化问题。当罚参数β>1时，证明了提出的算法—ALADMLD产生的序列收敛到非凸矩阵秩最小化问题的稳定点。利用随机数据和实际数据，将ALADMLD算法与基于核范数的先进算法进行数值实验比较，验证提出的算法高效性，同时表明了随着大数据问题的引入与推广，ALADMLD算法将比现有的LADM算法具有更广阔的应用前景。

参考文献：

[1]TOH K,YUN S.An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems[J].Pacific Journal of Optimization,2010,6(615-640):15.

[2]LIN Z,CHEN M,MA Y.The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices[J].arXiv preprint arXiv:1009.5055,2010.

[3]YANG J,YUAN X.Linearized augmented Lagrangian and alternating direction methods for nuclear norm minimization[J].Mathematics of Computation,2013,82(281):301-329.

[4]CHEN C,HE B,YUAN X.Matrix completion via an alternating direction method[J].IMA Journal of Numerical Analysis,2012,32(1):227-245.

[5]DUDIK M,HARCHAOUI Z,MALICK J.Lifted coordinate descent for learning with trace-norm regularization[C]//AISTATS-Proceedings of the Fifteenth International Conference on Artificial Intelligence and Statistics-2012.2012,22:327-336.

[6]SHERMAN J,MORRISON W.Adjustment of an inverse matrix corresponding to a change in one element of a given matrix[J].The Annals of Mathematical Statistics,1950:124-127.

[7]PENG C,KANG Z,LI H,et al.Subspace clustering using log-determinant rank approximation[C]//Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM,2015：925-934.

[8]LEWIS A,SENDOV H.Nonsmooth analysis of singular values:Part I:Theory[J].Set-Valued Analysis,2005,13(3):213-241.

[9]SHEN Y,WEN Z,ZHANG Y.Augmented Lagrangian alternating direction method for matrix separation based on low-rank factorization[J].Optimization Methods and Software,2014,29(2):239-263.

[10]YAN J,POLLEFEYS M.A general framework for motion segmentation:Independent,articulated,rigid,non-rigid,degenerate and non-degenerate[M]//Computer VisionCECCV 2006.Springer Berlin Heidelberg,2006:94-106.

[11]CHEN G,LERMAN G.Spectral curvature clustering (SCC)[J].International Journal of Computer Vision,2009,81(3):317-330.

[12]LIU G,LIN Z,YU Y.Robust subspace segmentation by low-rank representation[C]//Proceedings of the 27th international conference on machine learning (ICML-10).2010:663-670.

[13]VIDAL R,FAVARO P.Low rank subspace clustering (LRSC)[J].Pattern Recognition Letters,2014,43:47-61.

[14]ELHAMIFAR E,VIDAL R.Sparse subspace clustering:Algorithm,theory,and applications[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(11):2765-2781.

[15]FAZEL M.Matrix rank minimization with applications[D].Palo Alto：Stanford University,2002.

(责任编辑：傅游)

收稿日期：2016-01-08

基金项目：国家自然科学基金项目(11241005)

作者简介：陈勇勇(1989—)，男，山东泰安人，硕士研究生，研究方向为系统优化及应用、低秩矩阵恢复、分布式优化算法等. 王永丽(1977—)女，山东栖霞人，副教授，博士，研究方向为非线性优化理论与算法、分布式优化算法及数据挖掘等，本文通信作者.E-mail：wangyongli@sdkd.net.cn

中图分类号：N949

文献标志码：A

文章编号：1672-3767(2016)04-0106-08

Matrix Rank Minimization Algorithm Based on Augmented Lagrangian Alternating Direction Method

CHEN Yongyong，WANG Yongli，YU Huihui

(College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)

Abstract:To solve the matrix rank minimization problem with large singular values,the log-determinant function was used as a rank approximation instead of the nuclear norm and an augmented Lagrangian alternating direction method was proposed.When penalty parameter β>1,the sequence of iterations generated by the proposed algorithm was proved to be convergent to a stationary point of the original problem.Finally,numerical experiments were conducted based on real data and random data.The results demonstrate that the proposed algorithm is more efficient than the existing nuclear norm method in solving the problem of matrix rank minimization.

Key words:log-determinant function;nuclear norm;augmented Lagrangian alternating direction method;low rank representation