基于图像统计特征的新旧纸币识别算法

柳春华,姚建峰

(信阳师范学院 计算机与信息技术学院，河南 信阳 464000)

0 引言

自动清分、销毁银行回笼的易损纸币并补充等额的新币是银行、金融等机构中一项非常重要且繁重的工作[1,2].研究一种具有高准确率的新旧纸币自动识别方法以减轻汇兑纸币的工作强度量，对于银行或金融机构具有重要意义，并受到高度关注[3-5].

然而，训练模型用到的新旧纸币样本集中经常出现样本分布不均衡的情况，这容易导致传统的神经网络算法收敛于局部最优值，进而使得学习到的模型不能很好地拟合真实的样本分布[6].

基于以上问题，本文提出了一种基于图像统计特征的新旧纸币识别方法，该方法使用清分机计算未经流通新纸币的新旧特征块灰度平均值，并视其为该币种的标准亮度，以完成纸币新旧程度特征块的定位，进而求出其平均灰度值.对新旧识别的测量值进行计算和量化处理.依据纸币图像的均匀性特征对纸币图像的新旧程度进行判断.通过标准方差与间断强度对均匀性特征进行描述.分析了LVQ网络模型，LVQ网络中竞争层的所有神经元利用学习原型向量对输入空间进行分类[7].仿真实验结果表明，所提算法具有很高的识别正确率.

1 新旧纸币识别原理

因为不同面额纸币图像的大小有所差别，其新旧清分区域的位置也不同，所以需通过面额与面向的识别结果对新旧清分区域进行定位，从而实现新旧纸币的识别.

1.1 标准亮度的确定

首先利用清分机对100张未经流通新纸币的新旧特征块的灰度平均值进行计算，将其平均值看作是该币种的标准亮度.具体步骤如下：

(1)通过面额面向识别结果对新旧程度特征块进行定位，用100元面值纸币举例说明，新旧程度特征块用图1进行描述.

图1 损伤特征块定位结果Fig. 1 Location of the damaged feature blocks

(2)求出20张纸币新旧特征块的灰度平均值Gi(x,y)，i=1,2,…,20.用G(x,y)描述新币图像灰度，用W描述特征块的宽度，用L描述特征块的长度，则特征块的尺寸可描述成W×L.按照新旧程度特征块的定位结果，假设特征块左上角坐标是(x0,y0)，则特征块的平均灰度可由下式求出：

(3)标准亮度的计算:对将纸币新旧特征块的灰度平均值的平均值看作是该币种新旧识别的测量标准Vs：

(4)通过上述步骤分别求出各种面值纸币的标准亮度.

1.2 待测纸币新旧特征块亮度的确定

完成纸币新旧程度特征块的定位后，求出其平均灰度值.

设经噪声处理及倾斜校正等预处理后的待测纸币图像灰度是G′(x,y)，则新旧程度特征块的平均灰度可通过下式求出

1.3 新旧程度测量值计算

将VA和VS的比值Vnew作为新旧识别的测量值：

Vnew=VA/VS.

(4)

令100元纸币的新旧识别的测量值描述为：

Vnew=VA/VS100.

(5)

测量值Vnew越大，则纸币越新.

中国人民银行在2000年对流通纸币的整洁度进行了规范要求，提出流通中的纸币必须在7成新以上，7成新以下的即为旧币，不允许继续流通.通过Vnew值对纸币新旧识别测量值进行量化处理：

若0.9≤Vnew≤1，则认为待测纸币为9成新纸币；若0.8≤Vnew≤0.9，则认为待测纸币为8成新纸币；若0.7≤Vnew≤0.8，则认为待测纸币为7成新纸币.上述Vnew≥0.7纸币为可流通纸币，若Vnew<0.7，则认为该纸币是旧币，需回收.

2 基于图像统计特征的新旧纸币识别算法

2.1 纸币均匀性特征的采集

纸币图像是由大量细小线条及繁杂的纹理组成的，纸币图像边缘的清晰程度以及纹理区域的平滑程度均可有效体现出纸币的新旧程度[8].纸币流通时在正常磨损的状态下，其均匀性特征将越来越强，因此，可依据纸币图像的均匀性特征对纸币图像的新旧程度进行判断.

均匀性特征主要取决于从图像中采集的局部信息.均匀性特征主要包括标准方差与间断强度[9].标准方差是局部区域对比度的体现，而间断性是灰度级突变程度的体现，可利用对应区域应用边缘算子计算求出.

坐标(x,y)处的标准方差vx,y可利用下式求出：

像素点(x,y)处的间断性可用边缘值表示，当前常见的边缘提取算子为Sobel算子、Laplace算子、Canny算子等.考虑到本文无须获取精确的定位图像边缘，为了便于计算，选用Sobel算子对坐标(x,y)处的水平梯度Gx和垂直梯度Gy进行计算.图像在点(x,y)处的间断性特征可描述如下：

为了获取一致性计算结果，完成标准方差与间断值的归一化操作，可将图像中各坐标点的均匀性特征hx,y描述成：

式中：vmax=max{vx,y}，emax=max{ex,y}，0≤x≤M-1，0≤y≤N-1.图像中所有点的均匀性特征值均处于[0,1]区间中，一个像素点相邻的局部区域越一致，则均匀性特征值越小.若纸币图像上存在折痕或污损，则上述区域的均匀性将出现突变，纸币的均匀性强度将逐渐降低.

2.2 基于LVQ网络模型的纸币新旧分类方法

由Kohonen提出的LVQ神经网络模型是一种前向有监督的模式分类方法，它有三部分组成：向量输入层、竞争层、线性输出层，如图2所示.该模型主要通过三层结构完成工作，主要有几层数据联合工作，共同完成计算任务，但是层与层之间不是完全的信息通信过程.层与层之间如果无特殊说明，那么权值设为l，各输出神经元被描述成不一样的类[10].

假设网络输入层的输入向量用X=(x1,x2,…,xM)描述，其中，M表示输入神经元的总量；输入层与竞争层之间的连接权值矩阵可描述成

其中:i=1,2,…,P;j=1,2,…,M，用于描述竞争层第i个神经元与输入层第j个神经元之间的连接权值;P表示竞争神经元的总量，竞争层的输出向量可描述成

V=(v1,v2,…,vp);

竞争层和输出层神经元间的连接权值矩阵可描述成

图2 LVQ网络模型Fig. 2 LVQ network model

考虑到LVQ网络竞争学习与监督学习的规则，用一组正确网络行为对网络进行训练：

{x1,t1},{x2,t2},…,{xQ,tQ},

(10)

式中，各目标输出向量tj(j=1,2,…,Q)有且只有一个分量为1.为了保证学习过程的顺利进行，一般将各竞争层的神经元划分给一个输出神经元，从而完成矩阵W2的定义.W2的列代表子类，行代表类.W2的各列均仅存在一个1出现的行，用于描述该类属于该行表示的类，也就是：

W2是无法改变的，神经网络的学习即利用优化后的Kohonen规则使W1改变完成的.LVQ学习算法具体实现过程如下：

(1)假设变量与参量

x(n)=[x1(n),x2(n),…,xN(n)]T

是输入向量.Wij(n)=[wi1(n),wi2(n),…,wiN(n)]T是权值向量,i=1,2,…,M.选择学习速率的函数η(n),n表示迭代次数，N表示迭代总次数；

(2)对权值向量Wi(0)及学习速率η(n)=η(0)进行初始化处理；

(3)从训练集合中选择输入向量X；

(4)对欧氏距离进行计算，从而获取最小的标准：

‖X-Wc‖=min‖X-Wi‖.

(12)

检索竞争成功的神经元c，从而完成神经元的竞争；

(5)确定分类的正确性，通过下述规则对得到神经元的权值向量进行调增：

用Lwc描述和获胜神经元权值向量联系的类，用Lxi描述和输入向量相联系的类.

若Lxi=Lwc，则有：

Wc(n+1)=Wc(n)+η(n)[X-Wc(n)].

(13)

反之，如果Lxi≠Lwc，则有：

Wc(n+1)=Wc(n)-η(n)[X-Wc(n)].

(14)

其他神经元的权值则保持不变；

(6)对学习速率η(n)进行调整：

(7)判断迭代次数是否大于N，若n≤N，则重新进行步骤(3)，否则停止迭代.

3 仿真实验分析

为了验证本文算法的有效性，需要进行相关的实验分析.将6种人民币纸币作为研究对象，分别采用本文算法和传统算法进行对比分析.实验过程中的训练样本数量、测试样本数量及两种算法识别正确率的比较结果如表1所示.

表1中训练样本即用于作为参考纸币进行新旧训练的个数.新旧正确识别率即对空白区域新旧程度的判断结果.

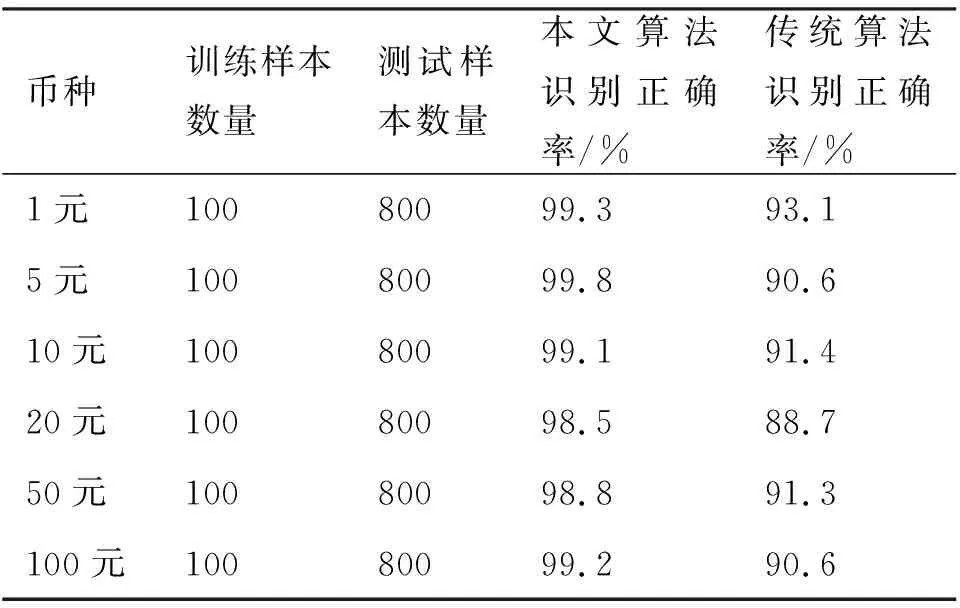
表1 本文算法和传统算法识别正确率结果Tab. 1 Accuracies achieved by the proposed algorithm and the traditional algorithm

分析表1可以看出，采用本文算法对新旧纸币进行识别的准确率明显大于传统神经网络算法，且一直大于传统算法，说明本文算法具有很高的识别精度.

为了进一步验证本文算法的有效性，在上述实验的基础上，对本文算法和传统算法完成识别所需的时间进行比较，获取的结果用图3进行描述.

分析图3可知，对同一币种相同数量样本进行识别时，本文算法所需的时间显著低于传统神经网络算法，说明本文算法不仅具有很高的识别精度，而且具有很高的识别效率，验证了本文算法的有效性.

图3 本文算法和传统算法所需时间比较结果Fig. 3 Comparison of time taken by this algorithm and the traditional algorithm

4 结论

提出一种基于图像统计特征的新旧纸币识别算法，利用清分机对未经流通新纸币的新旧特征块的灰度平均值进行计算，将其平均值看作是该币种的标准亮度，储存于机器内存中，完成纸币新旧程度特征块的定位后，求出其平均灰度值.对新旧识别的测量值进行计算和量化处理.依据纸币图像的均匀性特征对纸币图像的新旧程度进行判断.通过标准方差与间断强度对均匀性特征进行描述.分析了LVQ网络模型，LVQ网络中竞争层的所有神经元利用学习原型向量对输入空间进行分类.通过一组正确网络行为对网络进行训练，通过优化后的Kohonen规则实现LVQ网络的学习过程.仿真实验结果表明，所提算法具有很高的识别正确率.