基于FFT的正弦信号幅值估计研究

张　涛，杨炳恒，樊向党

(海军航空工程学院 青岛校区， 山东 青岛　266041)



基于FFT的正弦信号幅值估计研究

张涛，杨炳恒，樊向党

(海军航空工程学院 青岛校区， 山东 青岛266041)

摘要：为了实现基于FFT求取正弦信号频率的同时得到信号的幅值，推导了利用Matlab中FFT计算得到的幅值系数与信号真正幅值之间的关系，研究了在仿真中准确估计信号幅值的两个影响因素，即频率分辨率和信噪比。针对信号长度小于FFT计算点数时出现的估计误差，提出了先对信号进行周期延拓再进行FFT计算的方法，并对频率分辨率进行了重新定义，使其适用范围更广。针对信噪比在幅值估计中的影响进行了定量分析，确定了基于FFT估计信号幅值方法的适用范围以及不同信噪比下的估计精度。

关键词：FFT；幅值估计；频率分辨率；信噪比

本文引用格式：张涛，杨炳恒，樊向党.基于FFT的正弦信号幅值估计研究[J].兵器装备工程学报，2016(7):90-93.

Citationformat:ZHANGTao，YANGBing-heng，FANXiang-dang.ResearchonAmplitudeEstimationofSinusoidSignalBasedonFFT[J].JournalofOrdnanceEquipmentEngineering,2016(7):90-93.

在进行信号处理时，若信噪比较低将很难从时域中得到信号的参数信息，有时信号甚至完全被噪声所“淹没”，但是在频域却很容易得到信号的参数信息，尤其是信号的频率。因此，把时域信号转化为频域信号，对信号进行频谱分析是信号处理中最常用的方法。对于实际信号，一般都是在一段连续时间内，使电压(或电流)信号经过模数转换，从而得到采样点有限的离散时间信号，然后对所采集的离散信号进行傅立叶变换得到该信号的频谱。Matlab中FFT函数可以进行离散傅立叶变换(DFT)的计算，得到信号的频率成分。而信号的幅值同样是一个重要的参数，它代表了信号能量的大小，如果在得到信号频率的同时能够得到信号的准确幅值，将会给信号检测和参数估计带来很大的方便。

准确估计信号的频率是当前研究的一个热点问题，国内外很多学者做了大量的工作[1-8]。而对于信号幅值的估计却少有关注，仅仅有人做了一些理论上的推导[9]，而对在仿真中如何真正实现缺少深入的研究。

本文主要针对基于FFT估计正弦信号幅值展开研究，重点讨论在仿真中准确估计信号幅值的影响因素，针对信号长度小于FFT计算点数时出现的估计误差，提出先对信号进行周期延拓再进行FFT计算的方法，重新定义频率分辨率的概念，并对信噪比的影响进行定量分析，确定该方法的使用范围以及估计精度。

1基于FFT估计信号幅值的理论推导

正余弦信号用周期函数表示，即：

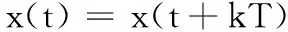
(1)

式(1)中：T是函数的周期，且k=0,1,2,…。

正余弦函数满足Dirichlet条件，可以分解为如下形式的傅立叶级数

(2)

式(2)中：ω=2π/T=2πf为信号的角频率； f=1/T为信号的频率；a0为信号的直流分量，an，bn和cn为各次谐波的系数，计算公式如下：

(3)

(4)

在Matlab中，对序列x(n)进行FFT计算后，其系数X(k)与式(4)的计算结果相同，只是n的取值范围为1≤n≤N。由文献[10]可得：利用Matlab中的FFT函数计算出各次谐波系数只需乘以2/N，再求模即可得到基于连续信号傅立叶级数等效的各次谐波幅值计算公式，得到各次谐波的真正幅值

(5)

2幅值估计的影响因素

假定仿真信号为：x(t)=10sin(2πf0t)+4sin(6πf0t)+8sin(12πf0t)， f0=200Hz为信号的基频，采样频率 fs=2 000Hz，进行N=1 000点的FFT计算，仿真结果如图1所示。

可以看到，在时域中很难分清各次谐波的频率和幅值，但是经过频谱分析，得到200Hz、600Hz和800Hz3根谱线，与仿真信号相对比，得到的200Hz和600Hz的频率估计值分别为10和4，没有误差，但是没有得到1 200Hz的谱线，这主要是由于1 200Hz> fs/2不满足奈奎斯特采样定理，得到的800Hz的谱线是由频谱混叠造成的。

如果频率估计值存在很大误差，其幅度估计值就没有实际意义。因此，首先要保证信号满足奈奎斯特采样定理，使采样频率 fs≥2f( f为信号的频率)，这是正确估计信号频率和幅值的前提。

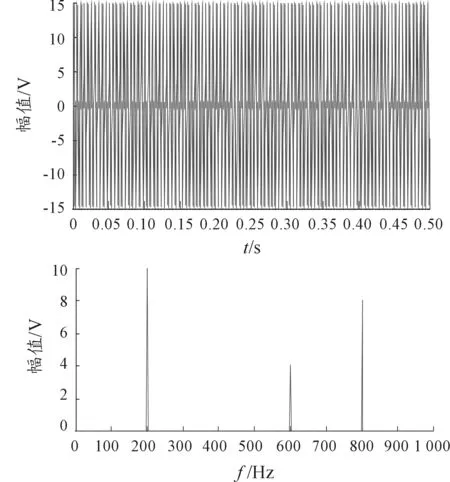
图1　仿真信号的时域波形及频谱分析

2.1频率分辨率的影响

在保证信号满足奈奎斯特采样定理后，还必须满足整周期采样才能准确估计信号的频率，否则将会产生频率泄露，造成“栅栏效应”。整周期采样的含义就是信号的频率应该是频率分辨率的整数倍，通常信号的频率分辨率定义为采样频率与FFT计算点数N的比值，即Δf= fs/N，所以信号的频率应该满足 f=MΔf=Mfs/N，其中M为整数。

上述仿真信号不变，对该信号进行N=1 000点的FFT计算，在N不变的情况下，通过改变采样频率 fs来改变频率分辨率，仿真结果如表1所示。

表1　不同频率分辨率下对信号幅值的估计

由于该信号的频率 f=200Hz，由表1可以看到，当对信号进行整周期采样，即频率分辨率为1、2、2.5时，频率估计值和幅值估计值都没有误差；当非周期采样，即频率分辨率为0.6、1.5、1.9时，频率估计值和幅值估计值都存在误差。因此，整周期采样也是基于FFT准确估计信号幅值的一个必要条件。

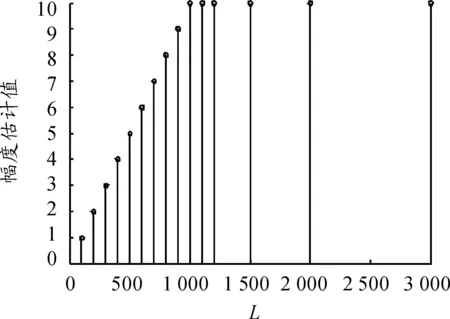
但上面的仿真程序中设定信号的长度L等于FFT的计算点数N。有时为了准确估计信号的频率，就必须提高频率分辨率，在采样频率固定不变的情况下，就必须增加FFT计算的点数，而在实际应用中，信号的长度往往不能随意改变，就有可能出现L

图2　信号长度改变时对信号幅值的估计

定义R为幅值估计值与真值的比例，则通过图2可以得到R与L和N的关系：当L

因为在Matlab中FFT函数是如下定义的：当L≥N时，首先对信号进行“截短”；当L

表2　L

当L=500，N=750时，频率为16Hz、30Hz和48Hz的3个信号都满足奈奎斯特采样定理，其中频率为30Hz的信号是频率分辨率1(Δf1=fs/L=6Hz)的整周期采样，频率为16Hz的信号是频率分辨率2(Δf2=fs/N=4Hz)的整周期采样，频率为48Hz的信号同时是频率分辨率1和频率分辨率2的整周期采样。仿真结果显示，频率为16Hz和30Hz的信号幅值估计存在误差，而频率为48Hz的信号幅值估计没有误差。当L=600，N=1 000时，可得到同样的结论。

可以发现，当L=N时，频率分辨率是唯一的，Δf= fs/N=fs/L，整周期采样的含义也比较明确；但是当L≠N时，频率分辨率不再唯一，而是存在两个频率分辨率(fs/N和 fs/L)，需要重新对整周期采样的含义进行说明，即需要对频率分辨率进行重新定义。首先定义物理分辨率Δf1=fs/L和计算分辨率Δf2=fs/N。由仿真结果可知，如果信号的频率仅仅是Δf1的整数倍或是Δf2的整数倍，幅值估计值仍然会有误差；如果信号的频率既是Δf1的整数倍又是Δf2的整数倍则估计值没有误差。所以把信号的频率分辨率重新定义为：Δf={Δf1,Δf2}的最小公倍数，只有信号的频率是该频率分辨率的整数倍时才能得到准确的幅值估计，否则会产生误差。该定义既适用于L≠N的情况，也适用于L=N的情况。

2.2信噪比的影响

以上所有的讨论都是在没有任何噪声干扰的前提下得到的结果，下面研究噪声干扰对信号幅值估计的影响。假定采样频率 fs=3 000Hz，信号频率 f=300Hz，L=N=500，满足奈奎斯特采样定理和整周期采样，在没有噪声干扰时得到的估计值为真值，通过给信号添加不同信噪比(SNR)的高斯白噪声，考虑到噪声的随机性，在相同信噪比下进行2 000次蒙特卡洛仿真，然后取平均值，仿真结果如表3所示。

可以看到，随着信噪比的增加，幅值估计误差越来越小。当SNR>30dB时，误差小于0.1%，可以忽略不计，近似为真值；当SNR<-20dB时，误差大于34.55%，已经远远偏离真实值，基于FFT估计信号幅值的方法不适用；当SNR>-9dB时，可以得到误差小于10%的幅值估计值；当SNR=0dB，即信号幅值与噪声幅值相当时，得到的幅值估计值误差为3.61%。

当对环境噪声不清楚时，可以通过给定一个已知信号，设定相应的频率采样率、信号长度和FFT计算的点数，使其满足奈奎斯特采样定理和整周期采样，对叠加噪声后的加噪信号进行FFT计算，基于FFT对信号幅值进行估计，通过得到的幅值估计误差与表3相比较，可以初步判定此时加噪信号的信噪比和环境噪声的幅值。

表3　不同信噪比下信号幅值估计误差的比较

3结论

基于FFT估计信号的幅值是一种简便的方法，利用Matlab中FFT函数计算出的信号幅值系数只需乘以2/N(N为FFT的计算点数)，再求模便可得到信号的真正幅值。但是采样频率 fs、信号频率 f、信号长度L和FFT计算点数N都会影响信号幅值的准确估计，本文通过对各种影响因素的分析研究，得到以下几个结论：

1) 没有噪声的情况下，只要满足奈奎斯特采样定理(即 fs≥2f)和整周期采样(即信号的频率应该是频率分辨率的整数倍)，便可以准确估计信号的幅值。针对L

2) 存在噪声干扰的情况下，不能得到准确的幅值估计。随着信噪比(SNR)的增加，信号幅值估计误差减小；当SNR>30dB时，估计值可近似为真值；当SNR<-20dB，即噪声幅值与信号幅值之比大于10倍时，误差大于34.55%，该方法已经不适用；当SNR>-9dB，即噪声幅值与信号幅值之比小于2.8倍时，该方法能得到误差小于10%的估计值。

参考文献：

[1]RIFEDC，BOORSTYNRR．Singletoneparameterestimationfromdiscrete-timeobservations[J]．IEEETransactionsonInformationTheory，1974，20(5)：591-598.

[2]KAYSM．Afastandaccuratesinglefrequencyestimator[J]．IEEETransactionsonAcoustics，Speech，andSignalProcessing，1989，37(12)：1987-1990.

[3]FITZMP．Furtherresultsinthefastestimationofasinglefrequency[J]．IEEETransactionsonCommunications，1994，42(2)：862-864.

[4]黄玉春，黄载禄，黄本雄，等．基于FFT滑动平均极大似然法的正弦信号频率估计[J]．电子与信息学报，2008，30(4)：831-835.

[5]李任科，何培宇，黄骏，等．高精度正弦信号频率估计算法研究[J]．四川大学学报：自然科学版，2011，48(3)：596-602.

[6]齐国清，贾欣乐．插值FFT估计正弦信号频率的精度分析[J]．电子学报，2004，32(4)：625-629.

[7]朱小勇，丁康．离散频谱校正方法的综合比较[J]．信号处理，2001，17(1)：91-97.

[8]李天昀，葛临东.两种快速频域细化分析方法的研究[J].振动与冲击，2006，26(9)：1192-1194，1216.

[9]李允公，刘杰，王瑞，等．频谱校正中频率-幅值估计的一种新方法[J]．东北大学学报:自然科学版，2007，28(11)：1612-1615.

[10]刘小群，周云波．基于Matlab的DFT及FFT频谱分析[J]．山西电子技术，2010(4)：48-49．

(责任编辑杨继森)

收稿日期：2016-02-17；修回日期：2016-03-17

作者简介：张涛(1983—)，男，博士，讲师，主要从事舰面航空保障、信号处理研究。

doi:10.11809/scbgxb2016.07.020

中图分类号：TN911

文献标识码：A

文章编号：2096-2304(2016)07-0090-04

ResearchonAmplitudeEstimationofSinusoidSignalBasedonFFT

ZHANGTao，YANGBing-heng，FANXiang-dang

(QingdaoBranch,NavalAeronauticalEngineeringInstitute,Qingdao266041,China)

Abstract:In order to obtain the frequency and amplitude of sinusoid signal based on FFT simultaneously, and the relationship between true signal amplitude and amplitude coefficient in FFT calculation based on Matlab was derived and then the two factors (frequency resolution and SNR) which influenced signal amplitude estimation accurately in simulation were discussed. Aiming at the estimation error resulted from that signal length is not equal to the calculation points in FFT, a method based on period extension before FFT calculation was presented, and frequency resolution which is widely used was redefined. Lastly, the SNR influence to amplitude estimation was analyzed quantitatively. Application scope and estimation accuracy for different SNR of this presented method were confirmed.

Key words：FFT; amplitude estimation; frequency resolution；SNR

【信息科学与控制工程】