混凝土梁抗扭性能分析及承载力修正公式

蔡雪峰，张三鹏，庄金平，杨尊煌，邱　豪

（1.福建工程学院土木工程学院，福建福州350118；2.福建省土木工程新技术与信息化重点实验室，福建福州350118）



混凝土梁抗扭性能分析及承载力修正公式

蔡雪峰1，2，张三鹏1，2，庄金平1，2，杨尊煌1，2，邱豪1，2

（1.福建工程学院土木工程学院，福建福州350118；
2.福建省土木工程新技术与信息化重点实验室，福建福州350118）

摘要：采用ABAQUS有限元软件对各种强度等级下各龄期钢筋混凝土梁的受扭性能进行分析。各龄期混凝土的本构关系采用塑性损伤模型，受拉指标采用断裂能。有限元分析结果表明：各龄期混凝土的抗扭承载力随龄期的增长而增长，开裂前早龄期混凝土梁的抗扭承载力主要由混凝土承担，钢筋的贡献很小；前3 d是混凝土扭矩增长最快的主要时间段，开裂扭矩和极限扭矩达到28 d的60%左右。最后，根据有限元参数分析结果，在现行规范的基础上提出了早龄期混凝土梁开裂扭矩和极限扭矩的修正公式。

关键词：龄期；钢筋混凝土梁；ABAQUS；开裂扭矩；极限扭矩；预测公式

模板早拆施工技术是一种加快模板周转、降低施工成本和缩短工期的先进施工方法，尤其是在早龄期混凝土中［1-4］。然而，模板早拆会导致混凝土结构或构件在龄期只有3 d甚至更早就会受到外界荷载的作用。目前有一些研究者［5-6］，对早龄期混凝土的力学性能指标及早龄期混凝土构件或结构的受弯性能进行了研究，但是对早龄期混凝土抗扭性能的研究尚未见到报道。实际工程中，有很多早龄期混凝土承受扭矩作用的例子，如:现浇框架边梁等。

为了更好地了解受扭作用对早龄期钢筋混凝土构件的力学性能影响，本文利用有限元软件ABAQUS对早龄期混凝土梁的抗扭性能进行模拟。为确保有限元模拟的正确性，首先对成熟混凝土梁的抗扭性能进行模拟并与他人的试验进行对比验证。在验证后的模型基础上，引用文献［7，8］早龄期混凝土的受压应力-应变关系，对早龄期混凝土梁抗扭性能进行模拟分析，研究强度等级为C20、C30和C40的混凝土梁在不同龄期（3、7、14和28 d）下的力学性能，并提出早龄期混凝土的开裂扭矩和极限扭矩预测公式，为工程人员提供参考。

1　有限元建模

1.1 材料本构关系

（1）混凝土

混凝土本构关系采用混凝土塑性损伤模型，C30和C40混凝土的早龄期单轴受压应力-应变关系参考文献［7］。文献［7］中无量纲受压应力-应变曲线采用了清华大学过镇海拟合公式:其中，

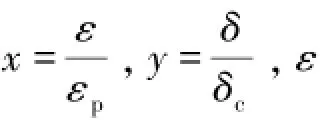
为混凝土应变，εp为混凝土峰值时对应的应变，δ为混凝土应力，δc为混凝土的峰值应力；a为混凝土初始弹性模量（E0）与混凝土峰值割线模量（Ep）的比值，下降段参数α根据混凝土的类型和水泥的编号来取值，本文参考文献［7］参数a取2.0，α取1.5。而C20混凝土的受压应力-应变曲线的取值参考文献［8］，方法与上述类似。

对于C30和C40混凝土早龄期弹性模量的取值，文献［7］对混凝土弹性模量试验数据建立了如下的函数关系公式:其中，Ect（）为混凝土不同龄期下的弹性模量，d为混凝土养护的龄期，fc（t）为混凝土在不同龄期下的抗压强度。C20、C30和C40混凝土的3、7、14和28 d弹性模量取值如表1。

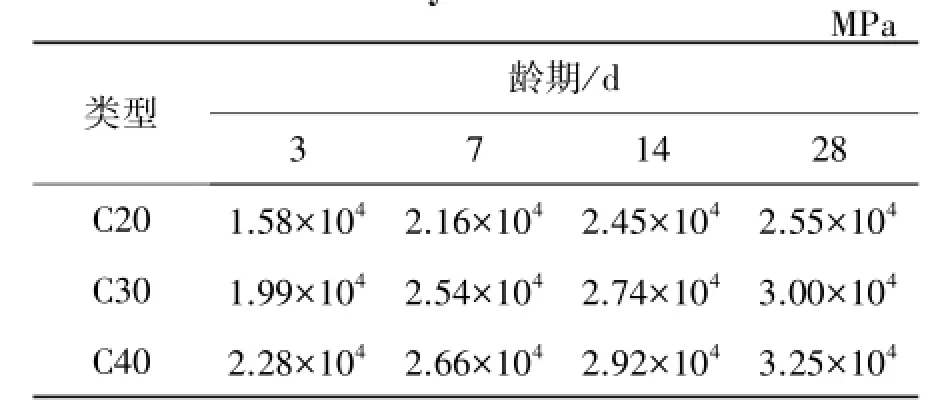
表1　混凝土弹性模量性能指标Tab.1 Elasticity modulus of concrete

对于混凝土塑性损伤模型受拉行为的本构关系，ABAQUS在计算方法上采用断裂能（GFI）类型，选择GFI类型是因为计算上更容易收敛。其中，GFI中屈服拉应力的确定采用公式［9］:其中:f′c为圆柱体混凝土的抗压强度，断裂能的取值参考文献［10］，按照以下公式:其中，Gf为混凝土的断裂能；Gf0=1.25 dmax+10，dmax为混凝土的最大骨料直径；fc为混凝土纵向峰值应力；混凝土的泊松比均为0.2。

（2）钢筋

箍筋和纵筋均采用二次塑流模型，应力-应变关系曲线的数学表达式如下。

1.2 单元类型的选择

在单元网格划分的时候优先选用减缩积分单元。同时，由于在做纯扭分析时，线性单元和二次单元的差距很小，因此从计算代价的方面考虑，在本模型中，混凝土采用C3D8R单元（八节点减缩积分三维实体单元）。钢筋中的箍筋和纵筋采用Truss，T3D2单元。

1.3 相互接触及网格划分

本模型ABAQUS模拟没有考虑粘结滑移作用，而是采用ABAQUS中的embedded region将钢筋和混凝土连接，并且在加载端面的参考点和约束端面的参考点用绑定约束（coupling）将参考点与混凝土面耦合在一起，将位移角施加在参考点上，这样可以更有利于荷载的传递。在网格划分过程中，对钢筋和混凝土采用单独划分网格，并且取钢筋和混凝土的精度均为45mm。

2　有限元模型验证

由于目前尚未有早龄期混凝土构件抗扭性能的报道，为验证有限元模型的准确性，暂采用成熟混凝土构件的抗扭性能试验数据对本文的有限元建模方法进行验证。算例采用文献［11］的试验数据，其钢筋混凝土梁截面为225mm×300mm，总长为2.5m，混凝土采用的是C40，箍筋材料属性如表2所示，配筋如图1所示。

表2　钢筋力学性能指标Tab.2 M echanical property of reinforced bar

图1　钢筋混凝土梁截面配筋图（单位：mm）Fig.1 Sectional reinforcement drawing of concrete rein forced beam（unit：mm）

混凝土本构模型采用混凝土塑形损伤模型，混凝土本构的应力-应变曲线与文献［11］一致。

图2给出了有限元计算结果与试验结果的对比。从图2中可以看出:有限元计算结果与试验值曲线总体上吻合得较好，有限元计算值和试验值的最大值偏差仅为4.8%。

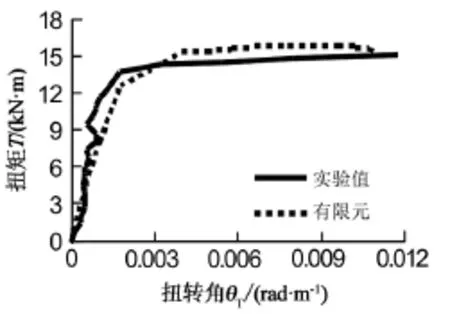
图2　有限元结果与试验值对比Fig.2 　Comparison of torque and　torsional angle between experimental value and finite element analysis value

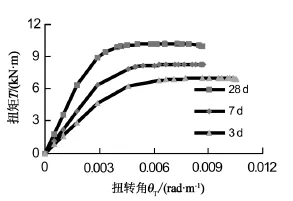
图3　C20不同龄期的扭矩-扭转角曲线Fig.3 Torque-torsion angle relationship of C20

图4　C30不同龄期的扭矩-扭转角曲线Fig.4 Torque-torsion angle relationship of C30

3　有限元结果分析

3.1 钢筋混凝土梁的扭矩-扭转角曲线结果

图3～5为各算例的扭矩-扭转角曲线。对于同种混凝土而言，混凝土的抗扭承载力随着龄期的增长而增长，其中28 d混凝土的抗扭承载力相比3 d混凝土抗扭承载力有明显提高；对于不同种混凝土而言，混凝土的抗扭承载力在同一龄期下随着混凝土强度的提高而增加，其中28 d混凝土的抗扭承载力增加明显。

图5　C40不同龄期的扭矩-扭转角曲线Fig.5 Torque-torsion angle relationship of C40

3.2 龄期对钢筋混凝土梁抗扭承载力的影响

钢筋混凝土梁的抗扭承载力一般由混凝土和钢筋两部分承担。对早龄期混凝土梁而言，其抗扭承载力与成熟混凝土的差异主要是混凝土承担部分的扭矩。本文主要分析各龄期对混凝土所承担扭矩的影响，分别对C20、C30和C40强度等级钢筋混凝土梁在3、7、14和28 d时纯扭性能进行分析。表3给出了有限元分析得到的各龄期算例的开裂弯矩和极限弯矩。

为判别混凝土所承担扭矩的大小，采用整体钢筋混凝土梁承担的扭矩减去钢筋笼承担的扭矩。通过ABAQUS分别建立钢筋混凝土梁和纯钢筋笼的纯扭模型，并得到各自的扭矩-扭转角曲线，通过曲线找出相同扭转角下各自的扭矩。此外，对于钢筋混凝土开裂扭矩的判定原则为: ABAQUS中出现主拉塑性应变时表示混凝土开裂［12］。

从表3中可以得出，龄期在7 d内时，混凝土的抗扭承载力增长速度最快，幅度最大；7 d之后，混凝土的抗扭承载力增长速度变慢，分析原因主要是，龄期在7 d内时，混凝土的内部构造不够稳定，混凝土的强度会大幅度迅速增长，抗扭承载力随着强度增加而增加；龄期超过7 d后，混凝土的内部构造趋于稳定，强度变化不大，抗扭承载力增长也不明显。

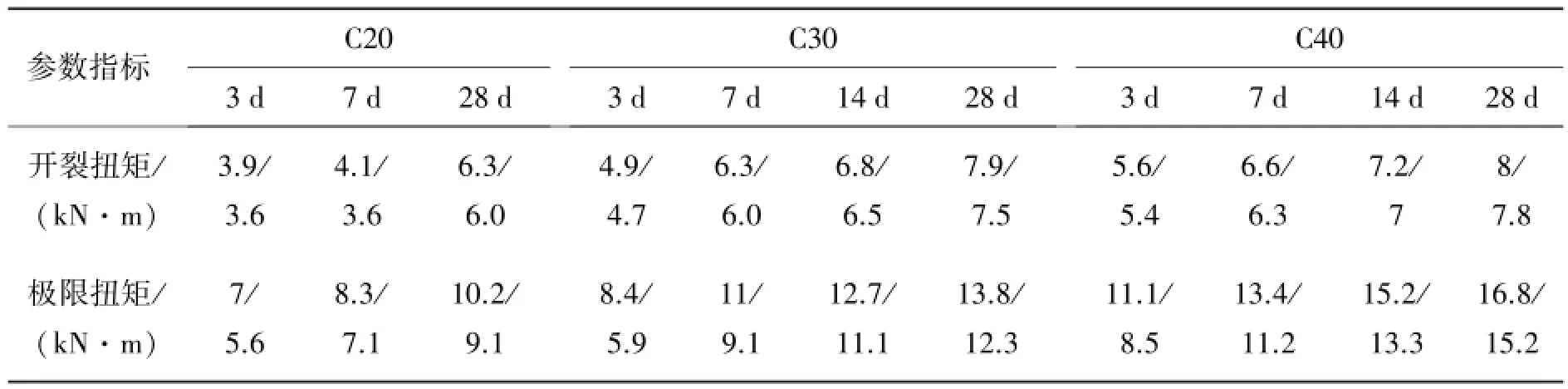
表3　钢筋混凝土梁在不同龄期下的开裂扭矩和极限扭矩Tab.3 Cracking torque and u ltimate torque of reinforced concrete beam at different ages

图6　龄期-Tcrc/Tcrc28曲线Fig.6 Age-Tcrc/Tcrc28relationship

3.3 龄期对混凝土承担开裂扭矩的影响

图6～7分别为各龄期-Tcrc/Tcrc28及各龄期-Tcr/Tcr28关系曲线图，表4为开裂前钢筋和混凝土应力分布表。其中，Tcrc为各龄期钢筋混凝土梁开裂时混凝土部分所承担的扭矩，Tcrc28为28 d成熟钢筋混凝土梁开裂时混凝土部分所承担的扭矩；Tcr表示各龄期钢筋混凝土梁开裂时所承担的扭矩，Tcr28为28 d成熟钢筋混凝土梁开裂时所承担的扭矩。从图10～11中可以看出，当龄期为3 d时，钢筋混凝土梁及其混凝土的开裂扭矩都能达到成熟混凝土的60%以上，从表4中可以看出，开裂前混凝土应力能达到总应力的95%左右，钢筋贡献很小。这说明前3 d是混凝土抗扭承载力的主要成长时段；开裂前混凝土承担主要的应力作用，因为受扭构件配置钢筋不能有效地提高受扭构件开裂时的扭矩。

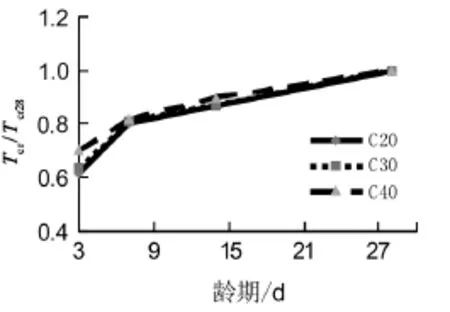
图7　龄期-Tcr/Tcr28曲线Fig.7 Age-Tcr/Tcr28relationship

表4　开裂前钢筋和混凝土应力分布情况表Tab.4 Stress distribution of rein forced bar and concrete before cracks

3.4 龄期对混凝土承担极限扭矩的影响

图8～9分别为各龄期-Tuc/Tuc28及各龄期-Tu/Tu28关系曲线图，表5为开裂后钢筋和混凝土应力分布表。其中，Tuc为各龄期钢筋混凝土梁开裂后混凝土部分所承担的最大扭矩，Tuc28为28 d成熟钢筋混凝土梁开裂后混凝土部分所承担的最大扭矩；Tu表示各龄期钢筋混凝土梁开裂后所承担的最大扭矩，Tu28为28 d成熟钢筋混凝土梁开裂后承担的最大扭矩。从图8～9中可以看出，混凝土承担的极限扭矩随着龄期的增长而增长，在龄期达到14 d后，混凝土承担的极限扭矩增长变化不大。各龄期混凝土部分所承担的极限扭矩低于钢筋混凝土梁整体所承担的极限扭矩，主要是因为受扭构件配置钢筋能较大幅度地提高受扭构件破坏时的极限扭矩值；从表5中可以看出，开裂后混凝土退出工作，钢筋承担主要的应力作用，进一步证实了配筋能较大幅度地提高钢筋混凝土的极限扭矩。

图8　龄期-Tuc/Tuc28曲线Fig.8 Age-Tuc/Tuc28relationship

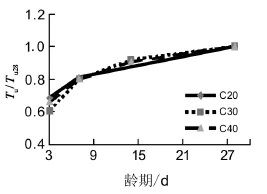
图9　龄期-Tu/Tu28曲线Fig.9 Age-Tu/Tu28relationship

表5　开裂后钢筋和混凝土应力分布情况表Tab.5 Stress distribution of reinforced bar and concrete after cracks

4　各龄期混凝土抗扭承载力机理分析

有限元分析结果表明:钢筋混凝土梁的破坏特征大体上相似，在混凝土开裂前钢筋应力很小；当混凝土开裂后，梁跨中附近形成一条斜裂缝，然后以螺旋形向两个面延伸，直至钢筋混凝土梁破坏。以C30钢筋混凝土梁在龄期为7 d时为例，给出有限元分析得到的应力云图。

（1）开裂前混凝土和钢筋的应力情况

图10～11为扭矩6.3 kN·m作用下混凝土和钢筋笼的应力云图。从图中可以看出，在开裂前混凝土所承受的应力总体上比钢筋大很多。C30的7 d试件，混凝土总体上受到的应力约为3.24MPa，钢筋的应力很小。其原因主要是，在钢筋混凝土梁受到的纯扭作用，扭矩荷载先传给混凝土部分，混凝土先于钢筋工作。

图10　混凝土开裂前的应力云图Fig.10 Stress nephogram of concrete before crackigng

图11　钢筋开裂前的应力云图Fig.11 Stress nephogram of reinforced bar before cracking

（2）开裂后混凝土和钢筋的应力情况

图12～13为扭矩11 kN·m作用下混凝土和钢筋笼的应力云图。从图中可以看出，混凝土开裂后，钢筋应力迅速增大，特别是在钢筋混凝土跨中的区域内，钢筋的应力达到了273.2MPa左右，混凝土的应力约为9.23MPa左右，钢筋的应力为混凝土应力的30倍左右。开裂后混凝土失去工作能力，完全由钢筋承担扭矩作用，因此开裂后钢筋承担主要的应力，其应力比混凝土的大得多。

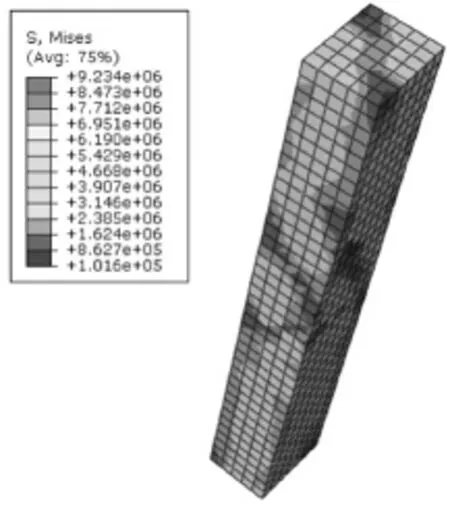
图12　混凝土开裂后的应力云图Fig.12 Stress nephogram of concrete aftercrack ing

图13　钢筋开裂后的应力云图Fig.13 Stress nephogram of reinforced bar after cracking

5　预测公式

现行《钢筋混凝土结构设计规范》将纯扭荷载作用下的抗扭承载力分为混凝土分项和钢筋分项，抗扭承载力公式仅运用于28 d成熟混凝土，对早龄期混凝土没有相关说明。对早龄期钢筋混凝土梁，主要变化在于混凝土强度较低，其承担的抗扭承载力也较小。因此，拟对规范中的混凝土抗扭承载力分项进行修正，得到早龄期钢筋混凝土梁的抗扭承载力预测公式。采用最小二乘法对表3中混凝土承担的抗扭承载力进行拟合，得到早龄期混凝土开裂预测公式和极限抗扭承载力预测公式，分别如式（6）和（7）所示。早龄期矩形截面钢筋混凝土纯扭构件的开裂抗扭承载力预测公式:

其中，Tcr为混凝土开裂扭矩设计值；t为混凝土的龄期；ft为28 d混凝土抗拉强度设计值；wt为截面受扭塑性抵抗矩。

早龄期矩形截面钢筋混凝土纯扭构件的极限抗扭承载力预测公式:

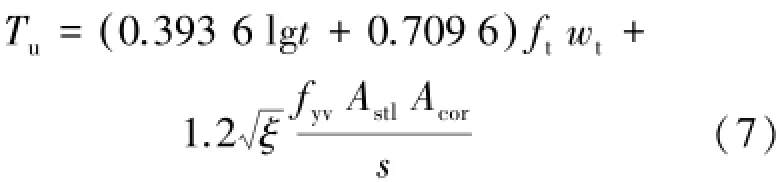
其中，Tu为矩形截面纯扭构件抗扭承载力设计值；t为混凝土的龄期；ft为28 d的混凝土抗拉强度设计值；wt为截面受扭塑性抵抗矩；fyv为箍筋的抗拉强度设计值；Astl为箍筋的单肢截面面积；Acor为核心截面部分的面积；s为箍筋的间距；ξ为抗扭纵筋与箍筋的配筋强度比。

其中早龄期混凝土的开裂抗扭承载力预测公式拟合程度达92.5%，极限抗扭承载力的预测公式达98%。图14和15分别给出有限元计算的开裂抗扭承载力和极限抗扭承载力和预测公式计算结果的对比情况，横坐标x为混凝土的龄期，横坐标y为28 d混凝土抗拉强度设计值，纵坐标z分别为开裂抗扭承载力和极限抗扭承载力，曲线为预测公式的计算结果，黑点为有限元的计算结果。

6　结论

图14　有限计算开裂扭矩与预测公式对比图Fig.14 Cracking torque com parison between the results via finite element analysis and prediction formula

图15　计算极限扭矩与预测公式对比图Fig.15 Ultimate torque com parison between the results via finite element analysis and prediction formula

1）混凝土的抗扭承载力随着龄期的增长而增长。前3 d是混凝土抗扭承载力增长最快的时间段，开裂扭矩能达到28d的50%～60%，极限扭矩能达到28 d的60%～70%。

2）在混凝土开裂前，混凝土承担主要的扭矩作用在95%左右，钢筋的贡献很小，不到5%。

3）根据有限元模拟的计算结果，给出的开裂扭矩预测公式和极限扭矩预测公式拟合精确度在合理范围内。

参考文献：

［1］糜嘉平.国内外早拆模板技术发展概况［J］.建筑技术，2011（8）:686-688.

［2］丁红岩，刘会勋，侯川.最不利条件下楼板模板早拆施工技术分析［J］.自然灾害学报，2009（4）:49-54.

［3］毛建斌.模板早拆体系在施工中的应用和发展［D］.天津:天津大学，2007.

［4］侯川.早拆模板施工技术研究［D］.天津:天津大学，2008.

［5］金贤玉，沈毅，李宗津，等.混凝土早龄期受力对后期性能的影响［J］.混凝土，2003（7）:35-37.

［6］王冬雁，吴岳刚，杨振坤，等.C80早龄期钢筋混凝土梁受弯性能试验研究［J］.工业建筑，2013，43（12）:82-87.

［7］田明革.钢筋混凝土框架结构施工期性能研究［D］.长沙:湖南大学，2008.

［8］刘会勋.二向应力状态下早龄期C20混凝土的破坏准则和本构关系试验研究［D］.天津:天津大学，2009.

［9］沈聚敏，王传志，江见鲸.钢筋混凝土有限元与板壳极限分析［M］.北京:清华大学出版社，1993.

［10］Genikomsou A S，Polak M A.Finite elementanalysis of punching shear of concrete slabs using damaged plasticitymodel in ABAQUS［J］.Engineering Structures，2015，98:38-48.

［11］李红波.型钢混凝土构件受扭试验研究［D］.重庆:重庆大学，2008.

［12］王文达，杨全全，李华伟.基于分层壳单元与纤维梁单元组合剪力墙滞回性能分析［J］.振动与冲击，2014，33（16）: 142-149.

（责任编辑：陈雯）

中图分类号：TU711

文献标志码：A

文章编号：1672-4348（2016）03-0205-07

doi:10.3969/j.issn.1672-4348.2016.03.001

收稿日期:2016-06-02

基金项目:国家自然科学基金（51478119）；福建省科技厅项目（2013H6003）；福建工程学院科研发展基金（GYZ15098）

第一作者简介:蔡雪峰（1956-），女，福建福鼎人，教授，硕士，研究方向:现代施工与信息化。

Finite elem ent analysis of anti-torsional performance（behaviour）and bearing （torsional）capacity formula correction of reinforced concrete beam

Cai Xuefeng1，2，Zhang Sanpeng1，2，Zhuang Jinping1，2，Yang Zunhuang1，2，Qiu Hao1，2
（1.College of Civil Engineering，Fujian University of Technology，Fuzhou 350118，China；2.Fujian Provincial Key Laboratory of Advanced Technology and Informationization in Civil Engineering，Fuzhou 350118，China）

Abstract:The torsional behaviour of reinforced concrete beam at different ages was analysed by ABAQUS finite element software under different strength grades.The concrete damaged plasticity modelwas employed in constitutive relationship among different ages，while tensile fracture energy was used as tensile indexes（indicators）.The（finite elementanalysis）results indicate that the antitorsional capacity of reinforced concrete at different ages increases with the growth of ages.Furthermore，the torsional capacity of the reinforced concrete at the early age ismainly taken by concrete and little by steel bar before it cracks.Meanwhile，the first three days is the fastest time for concrete to increase torque capacity.The concrete’s cracking torque and ultimate torque can reach 60%at28 days.Finally，the improved cracking torque and ultimate torque formula of concrete beam at early ages are also proposed based on available standards.

Keywords:age；reinforced concrete beam；ABAQUS；cracking torque；ultimate torque；prediction formula