利用模糊数学方法区分56冲、81步射击弹壳（一）

崔红玲 何兴周

（广东省清远市刑警支队 511500）

利用模糊数学方法区分56冲、81步射击弹壳（一）

崔红玲 何兴周

（广东省清远市刑警支队 511500）

本文利用射击弹壳上的抛壳口痕迹痕迹，通过对它们的有关特征参数（主、次口痕高、偏度、倾斜方向）进行处理，应用模糊数学中的最大隶属原则、聚类分析、模糊矩阵合成等方法进行模糊运算，较成功地区分了发射枪种。

主抛壳口；次抛壳口；击针头；模糊矩阵；矩阵合成；模糊评判

1 基础理论依据

1.1 枪弹痕迹依据

为应用模糊数学的方法区分56冲和81步的射击弹壳，我们选取了射击弹壳上的主抛壳口、次抛壳口两大类痕迹，并对其进行测量、分析。

1.1.1 痕迹的形成、性质及其特征

（1）主抛壳口痕迹

该痕迹是弹壳在抛出过程中第一次与机匣盖的棱边碰撞形成的粗大、明显、有一定深度的长条形线痕。56冲射击弹壳主抛壳口痕有一定宽度、痕迹较浅，81步主抛壳口痕为长条形、较深（如图1～4）。根据上述定位标准，56冲主抛壳口痕迹在5时位左右，81步主抛壳口痕迹在4时位左右。

图1 56冲主抛壳口痕迹

图2 56冲次抛壳口痕迹

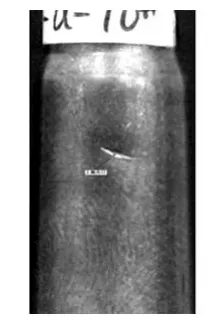
图3 81步主抛壳口痕迹

图4 81步次抛壳口痕迹

（2）次抛壳口痕迹

在实验中，发现有两种痕迹相对稳定，且出现率较高，为方便表述，我们分别将其命名为次抛壳口A、B痕迹。这两种痕迹是弹壳在抛出时与机匣盖的棱边连续碰撞，并发生自身扭转运动形成的擦划线痕及点状磕碰痕迹。根据上述定位标准，56冲次抛壳口A痕迹在8～9时位，B痕迹在7～8时位；而81步次抛壳口A痕迹在7～8时位，B痕迹在6～7时位（见图 1～4）。

1.1.2 痕迹特征参数的选择与测量

（1）抛壳口特征参数

主抛壳口高度 h1、偏度 s1；次抛壳口 A 高度 h2、偏度 s2，B 高度 h3、偏度s3。在立体显微镜下，观看主抛壳口痕迹形态确定其中心，以弹壳底面为水平面，用垂直游标卡尺测量弹壳底面至主抛壳口痕迹中心的垂直高度h1；利用弹壳角度测量仪，以抛壳挺痕迹为12时位，确定主抛壳口痕迹中心所在时位，测量主抛壳口与抛壳挺差角。次抛壳口痕迹测量标准与测量方法相同。

（2）主抛壳口倾斜方向

在立体显微镜下观看主抛壳口痕迹形态，以弹壳轴线为中线，确定主抛壳口痕迹倾斜方向。从左上至右下为右倾，从右上至左下为左倾，如图5。

1.2 模糊数学理论

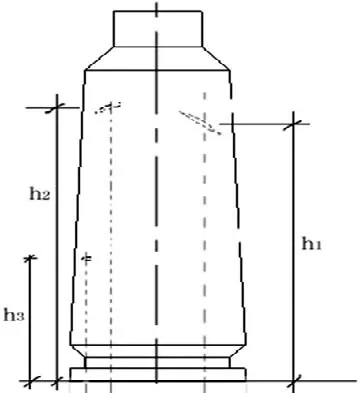
图5

最大隶属原则：

设ui∈（U），U为识别对象全体，Ui（i=1，2，…n）为U中归类的子集。Uo∈U为待归类的任意元素。Uo隶属于Ui类的隶属度为μui（Uo），其值为[0，1]，表示Uo属于Ui类的程度。定义：μui（Uo）=Max[μu1（Uo），μu2（Uo），…，μun（Uo）]，则认定Uo相对隶属于Ui类的程度为最大，并称这种隶属关系为最大隶属原则。

然后按最大隶属原则进行归类。其具体步骤如下：

（1）确定元素Uo的特征隶属度μui（Xk）

确定某元素Uo属于某一类别Ui的隶属度μui（Uo）通常由描述元素特征的有关参数X1，X2…Xm与归类类别的相应参数X01i，X02i…Xomi建立数学模型，求出相对应参数表示某一特征的隶属度μui（X1），μui（X2）…μui（Xm）。

（2）求某一特征的加权隶属度rxμui（Xk）

根据隶属度的定义，某一元素对某一类别的隶属度μui（Uo）∈[0，1]，即不可能超过1。而μui（Uo）应为各特征隶属度μui（Xk）之和；由于各特征在归类过程中的作用大小不同，所以人们通常用加权的方法，分别赋不同的权重于各特征，则得到特征加权隶属度Vkμui（Xk），这里

（3）求某一元素Uo的特征综合隶属度μui（Uo）

（4）按最大隶属度原则进行归类

2 前期数据处理

2.1 特征参数散布中心的确定

对5支56冲发射的250枚射击弹壳和5支81步发射的248枚射击弹壳上主、次抛壳口痕迹的出现率进行统计，并对各种痕迹的相关特征参数进行求平均值运算，确定各特征参数的散布中心。

如表1所示，射击弹壳主抛壳口痕迹高度h01，其偏离基线的偏度s01；次抛壳口A痕迹高度h02，其偏离基线的偏度s02；主抛壳口痕迹与次抛壳口A痕迹的高度差△h01；主抛壳口痕迹与次抛壳口A痕迹的偏度差△s01；次抛壳口B痕迹的高度h03，其偏离基线的偏度s03；主抛壳口痕迹与次抛壳口B痕迹的高度差△h02；主抛壳口痕迹与次抛壳口B痕迹的偏度差△s02；次抛壳口A痕迹与次抛壳口B痕迹的高度差△h03，次抛壳口A痕迹与次抛壳口B痕迹的偏度差△s03为：

2.2 确定各个特征参数的分配权重

求出每个枪种发射的弹壳上的所有特征的总和，作为分母，将每个特征参数出现的次数与之比较，所得数值即为该特征参数的分配权重。两组28个数据按与前述14个特征参数相关的顺序排列如下：

表1

3 应用模糊数学理论区分发射枪种

最大隶属原则法：

随机抽出5枚待归类弹壳，各特征参数如下：

表2

3.1 确定待测归类射击弹壳的特征隶属度

隶属度即是指某一特征参数分配在其散布中心附近的程度。根据公式：

分别求出相对于56冲和81步的主抛壳口痕高度隶属度μA（h1），主抛壳口痕偏度s1隶属度μB（s1），次抛壳口痕A高度h2隶属度μC（h2）、偏度s2隶属度μD（s2），主抛壳口痕与次抛壳口痕A高度差△h1隶属度μE（△h1）、偏度差△s1隶属度μF（△s1），次抛壳口痕B高度h3隶属度μG（h3）、偏度s3隶属度μH（s3），主抛壳口痕与次抛壳口痕B高度差△h2隶属度μI（△h2）、偏度差△s2隶属度μJ（△s2），次抛壳口痕A与次抛壳口痕B高度差△h3隶属度μK（△h3）、偏度差△s3隶属度μL（△s3）如下：

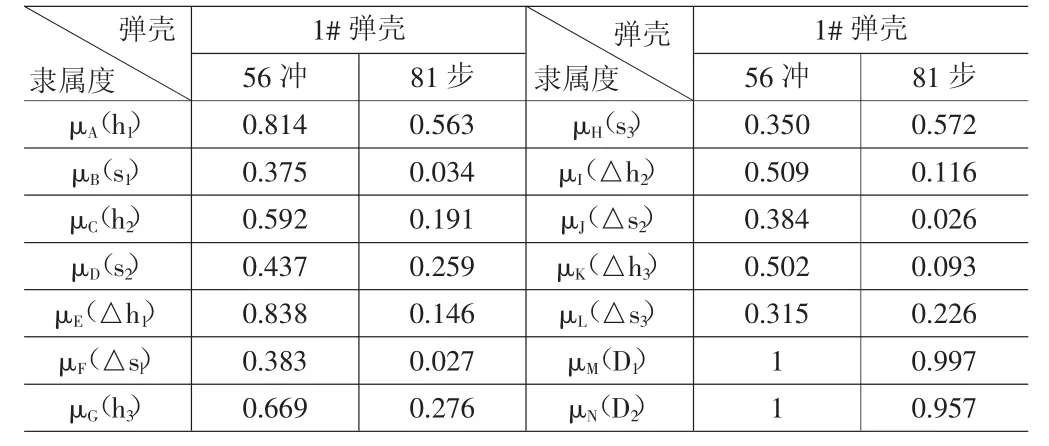
表3

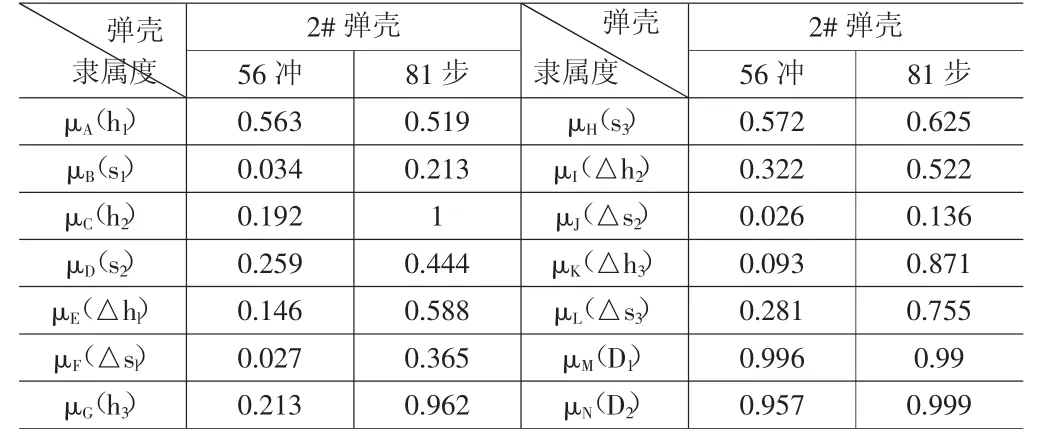
表4

3.2 求特征综合隶属函数

按公式：ui（Uo）=V1μA（h1）+V2μB（s1）+V3μC（h2）+V4μD（s2）+V5μE（△h1）+V6μF（△s1）+V7μG（h3）+V8μH（s3）+V9μI（△h2）+V10μJ（△s2）+V11μK（△h3）+V12μL（△s3）+V13μM（D1）+V14μN（D2）

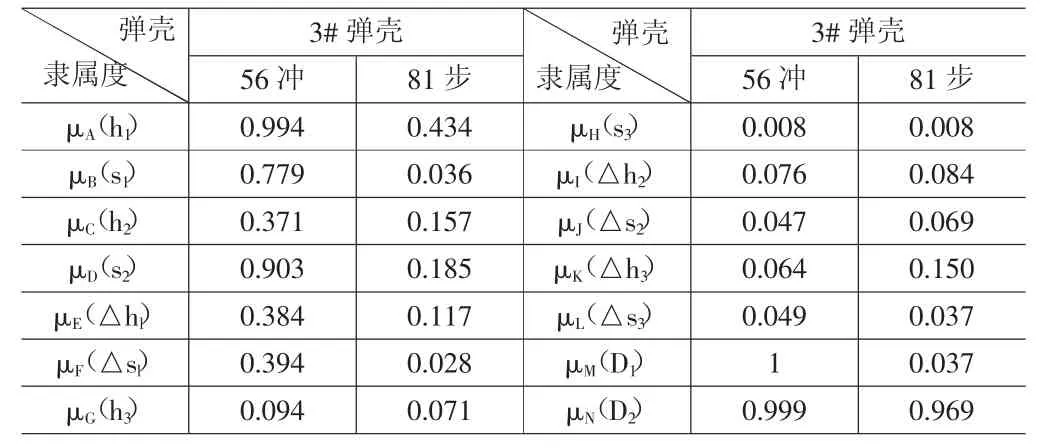
表5

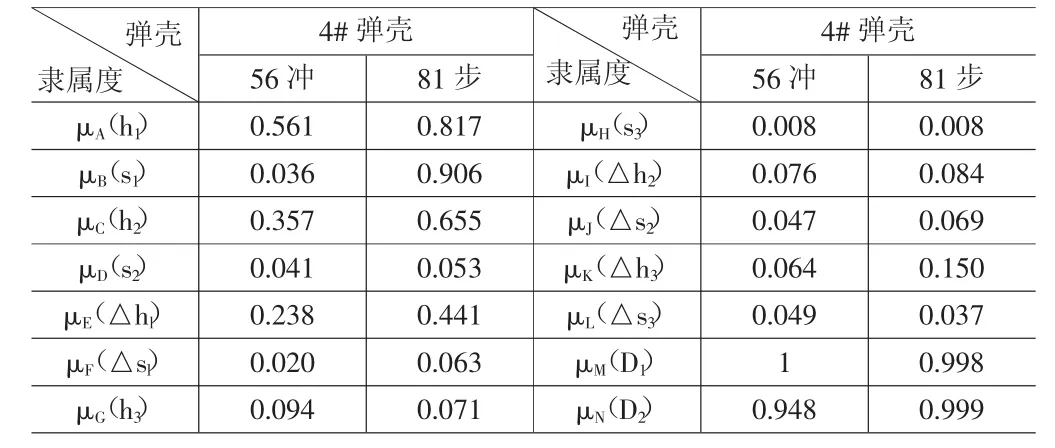
表6

表7

计算出八个待归类弹壳相对于56冲和81步的特征综合隶属函数如表8所示。

表8

3.3 按最大隶属原则进行归类

根据上表中数值对射击弹壳进行的归类。

对于 1 号弹壳：max[μ56（1#），μ81（1#）]=max（0.664，0.448）=0.664=μ56（1#）则得1#弹壳是56冲发射的。同理可以对其他弹壳进行归类。认定 1#3#，5#，为 56 冲发射的；2#，4#，为 81 步发射的。

3.4 说明

（1）当待归类弹壳无次抛壳口痕A，只有次抛壳口痕B时，则分别赋值 h2，S2，△h1，△S1，△h3，△S3为零；当待归类弹壳无次抛壳口痕 B，只有次抛壳口痕 A 时，则分别赋值 h3，S3，△h2，△S2，△h3，△S3为零；当待归类弹壳无次抛壳口痕A，同时无次抛壳口痕B时，则分别赋值h2，S2，△h1，△S1，h3，S3，△h2，△S2，△h3，△S3为零。这样，由于散布中心数值较大，将上述特征参数赋值为零后，据公式计算出的隶属度相对其它隶属度差了两个数量级，不影响归类结果；

（2）理论上来讲，同一特征参数相对于56冲和81步不会出现相等的隶属度，但是由于上述赋值为零的前提，和数据处理时采用四舍五入的方法，只取小数点后三位，所以出现个别相等数值。

[1]张清武，王庆丰.公安模糊数学.中国刑警学院，1995，10：18～136.

D918.9

A

1004-7344（2016）33-0294-02

2016-11-10