多领航者网络化系统的动态群集运动
王付永,杨洪勇,韩辅君
(鲁东大学信息与电气工程学院,山东烟台 264025)
多领航者网络化系统的动态群集运动
王付永,杨洪勇,韩辅君
(鲁东大学信息与电气工程学院,山东烟台 264025)
针对时变动态切换拓扑下具有多个领航者的网络化系统群集运动问题,本文分别给出了一阶/二阶网络化系统的控制算法,并对所提出的控制算法进行了理论分析.运用现代控制理论、代数图论和矩阵论等分析工具,研究了当通信拓扑为动态联合连通时,系统可以实现群集运动,即系统的运动轨迹都收敛到由多个领航者构成的凸包中.通过对系统信息拓扑连通部分的进一步研究,得到了二阶网络化系统群集运动的约束条件.最后应用仿真实验验证了结论的正确性.
多领航者;网络化系统;群集运动;联合连通
1 引言
近年来,基于生物学启发的网络化系统分布式协调问题引起了众多研究者的广泛关注.在生物学、社会行为学、计算机图形学、通信网络等分布式控制领域的应用,大大推动了对网络化系统协同运动的深入研究.
网络化系统的一致性问题是分布式协同控制的一个重要研究方向[1~3].包容控制是一种具有多领航者的类一致性问题,其目的在于通过设计跟随者的控制协议使得跟随者最终收敛到领航者围成的某一目标区域内(领航者围成的凸包内).具有单领航者的包容控制实际上是一致性跟踪问题[4~6],具有多领航者的群集运动控制主要包括一阶网络化系统[7~10]、二阶网络化系统[11~13]和非线性系统[14].多领航者网络化系统的群集运动控制,就是具有多个领航者的网络化系统的包容控制问题.
文献[7]首先研究了无向连通网络中一阶网络化系统的包容控制问题,并利用偏差分方程的方法证明了控制算法的有效性.文献[8]讨论了一阶网络化系统的包容控制问题,并证明了当网络拓扑连通时系统可以实现包容控制.文献[9]研究了有向网络中固定拓扑和切换拓扑两种情况下一阶网络化系统的包容控制问题,并给出了系统收敛的充要条件.文献[10]研究了一阶线性网络化系统的分布式包容控制问题,提出了一种基于动态输出反馈的控制算法.文献[11]针对具有动态领航者的二阶网络化系统,分别提出了连续渐近包容控制算法和离散渐近包容控制算法.文献[12]研究了随机切换拓扑下二阶网络化系统的包容控制问题,并提出了一种基于不可约马尔科夫链信息拓扑的包容控制算法.文献[13]研究了二阶网络化系统的分布式包容控制问题,并给出了系统收敛的充分必要条件.文献[14]研究了非线性网络化系统的姿态包容控制问题,并提出了两种有限时间收敛的包容控制算法.
在实际应用中,通信拓扑结构通常是变化的,不连通的.在网络拓扑为联合连通条件下,文献[15]研究了一阶时滞网络化系统的一致性问题,并扩展到了二阶时滞网络化系统[16].文献[17]研究了时滞系统和非时滞系统两种情况下具有动态领航者的二阶网络化系统的一致性跟踪问题.文献[18]则研究了非线性网络化系统的一致性跟踪问题.因此在系统拓扑不连通的情况下,研究具有多个领航者的网络化系统的群集运动控制问题具有十分重要的意义.
本文研究在联合连通条件下由多个领航者引导的一阶和二阶网络化系统的群集运动问题.本文的创新点在于假设系统信息拓扑不连通的情况下,提出了具有多领航者的网络化系统在联合连通条件下的群集运动控制算法,应用矩阵理论和现代控制理论,研究了算法的收敛性.
2 代数图论
设G=(V,ω,A)是n个节点的权重无向图,V={1,2,…,n}为一个顶点(或节点)集合,ω⊆V×V为一个边的集合,A=[aij]∈n×n为权重邻接矩阵.对于∀i∈V,aii=0;对于∀i,j∈V,i≠j,若(i,j)∈ω,则aij>0,否则,aij=0.节点i的邻居集合定义为Ni={j∈V|(i,j)∈ω}.定义D=diag{d1,d2,…,dn}∈n×n为图G的度矩阵,其中aij,i=1,2,…,n.权重图G的Laplacian矩阵定义为:L=D-A∈n×n.
定义1如果网络化系统中的一个自主体至少存在一个邻接成员,则称为跟随者,否则称为领航者.
定义2[16]设拓扑图G1,G2,…,Gm具有相同的顶点集V,其并集记为G1-m,它的节点集是V,边集是所有图G1,G2,…,Gm的边的并集,它的第i个节点和第j个节点间的链接权重是图G1,G2,…,Gm第i个节点和第j个节点间所有的链接权重之和.称G1,G2,…,Gm为联合连通,如果它们的联合图G1-m是连通的.
考虑一组无穷有序的有界连续时间段[tr,tr+1),r=1,2,…,且t1=0,tr+1-tr≤T1,T1>0.假设每个时间段[tr,tr+1)中存在一组非重叠的有限子序列[tr,j,tr,j+1),j=1,2,…,mr,且系统拓扑在[tr,j,tr,j+1)内保持不变,其中tr,1=tr,tr,mr+1=tr+1,tr,j+1-tr,j≥T2,T2>0.令σ(t):[0,+∞)→Γ,Γ={1,2,…,N}为一个分段切换常函数,N为总拓扑数.本文研究由n个跟随者和m个领航者组成的分布式网络化系统.系统在t时刻的信息拓扑图记为Gσ(t),相应的Laplacian矩阵记为Lσ(t).其中,由n个跟随者构成的信息拓扑图记为GFσ(t),相应的Laplacian矩阵记为LFσ(t).
3 一阶多领航者网络化系统群集运动控制算法分析
考虑一个由n个跟随者和m个领航者构成的网络化系统.跟随者集合与领航者集合分别记为F={1,2,…,n}和Υ={n+1,n+2,…,n+m}.假设一阶网络化系统动态方程描述为:
(1)
其中,xi(t)∈,ui(t)∈分别为网络化系统中第i个自主体的状态和控制输入.
假设1由n个跟随者和m个领航者构成的网络化系统拓扑在非重叠时间区间[tr,tr+1),r=1,2,…内为联合连通的.
假设2非重叠时间区间[tr,j,tr,j+1)⊂[tr,tr+1),j=1,2,…,mr内,分布式网络化系统存在一连通子集.连通子集中任意一个跟随者i,至少与一个领航者j之间存在一条路径.
假设一阶网络化系统控制协议为:
(2)
根据定义3,系统(1)可描述为:
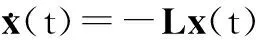
(3)
其中,x(t)=[x1(t),…,xn(t),xn+1(t),…,xn+m(t)]T.
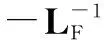
定义4[9]设集合X={x1,x2,…,xm}为实向量空间V⊆的子集,X的凸包定义为}.

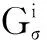
(4)
(5)
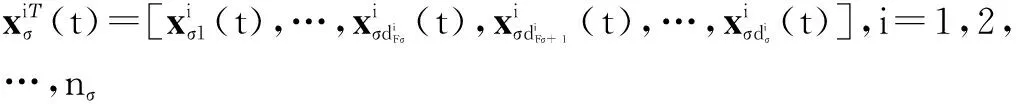
在动态切换拓扑下网络化系统式(3)可描述为:
(6)
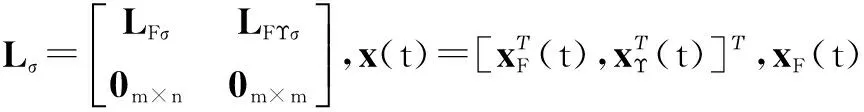
在每个时间段[tr,j,tr,j+1)内,系统(6)可以被分解为nσ个子系统,即
(7)

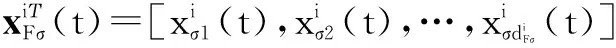

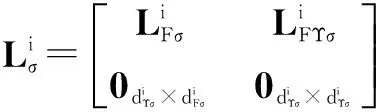
定理1考虑由n个跟随者和m个领航者构成的一阶动态网络化系统,且满足动态方程式(1),在假设1和假设2条件下,则系统在控制协议(2)下能够实现渐近包容控制.
证明由式(7),得

即有
(8)
在时间段[tr,j,tr,j+1)内解式(8)可得
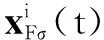

(9)


4 二阶多领航者网络化系统群集运动控制算法分析
假设网络化系统由n个跟随者和m个领航者组成,其二阶网络化系统动态方程描述为:

i=1,…,n,n+1,…,n+m
(10)
其中,qi(t)∈,pi(t)∈,ui(t)∈分别为网络化系统中第i个自主体的位置信息、速度信息和控制输入.假设二阶网络化系统控制协议为:
+γ(pi(t)-pj(t))], i∈F
pi(t)=0, i∈Υ
(11)
其中,α,β,γ均为常数.
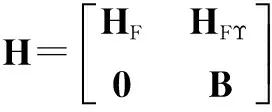
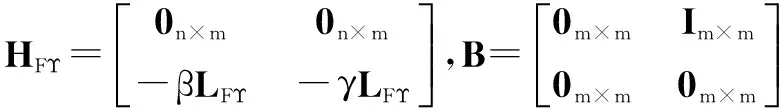
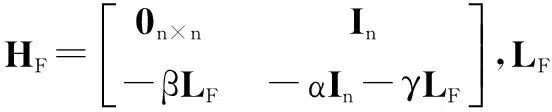
根据式(10)和式(11),二阶网络化系统可描述为:
(12)
其中,
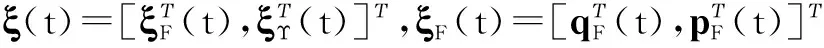
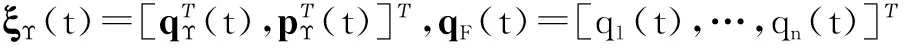
pΥ(t)=[pn+1(t),…,pn+m(t)]Τ,ξF(t)表示跟随者的信息,ξΥ(t)表示领航者的信息,qF(t)和qΥ(t)分别表示跟随者和领航者的位置信息,pF(t)和pΥ(t)分别表示跟随者和领航者的速度信息.采用与式(4)相同的处理方法,存在一个置换矩阵Eσ,使得
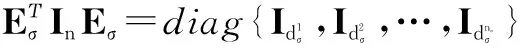
(13)
(14)
(15)
其中,
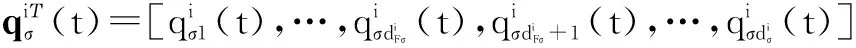

i=1,2,…,nσ.
在每个时间段[tr,j,tr,j+1)内,系统(12)可以被分解为nσ个子系统,即
(16)
其中,
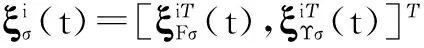
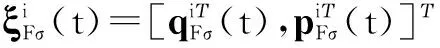

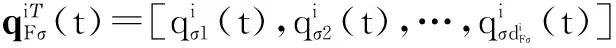
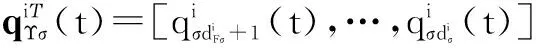
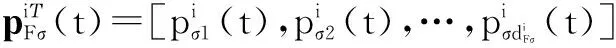

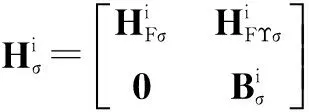
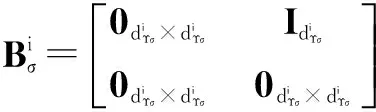
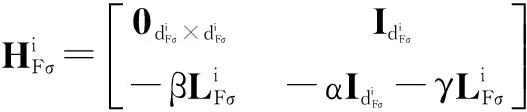

定理2考虑由n个跟随者和m个领航者构成的二阶动态网络化系统,且满足动态方程式(10),在假设1和假设2条件下,且对任意的t∈(0,+∞)满足
(17)
则系统在控制协议(11)下能够实现渐近包容控制.其中,μk表示矩阵(-LFσ)的特征值.
证明由式(16),得
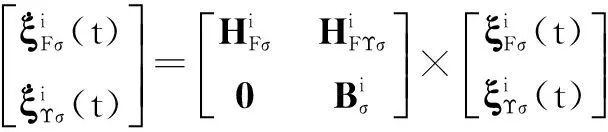
(18)
(19)
由式(18),得
由式(19),得
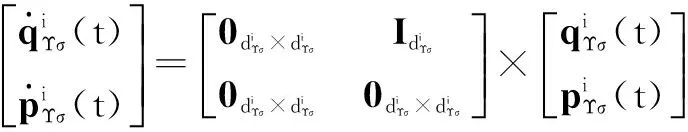

在时间段[tr,j,tr,j+1)内解式(18)可得
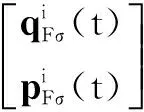


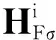
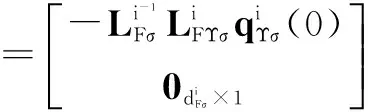
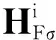
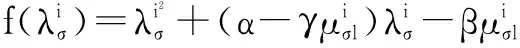
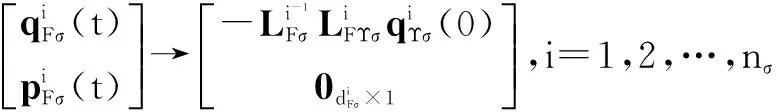
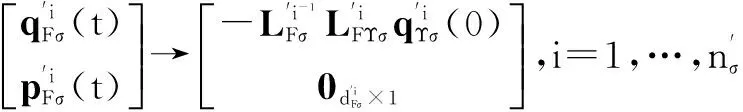
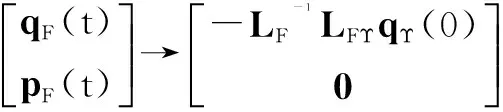
5 实例分析
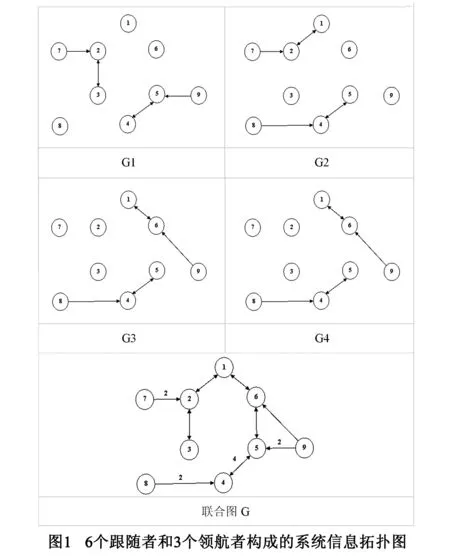
考虑3个领航者和6个跟随者,领航者集合和跟随者集合分别为Υ={7,8,9}和F={1,2,3,4,5,6},其动态拓扑图如图1所示.假定系统互连拓扑图在时刻t=kT,k=0,1,…,在拓扑图G1~G4中随机地切换,T取为0.5s.系统互连拓扑图的连接权重下图中已标记,未标记的默认为1.
5.1一阶网络化系统数值仿真
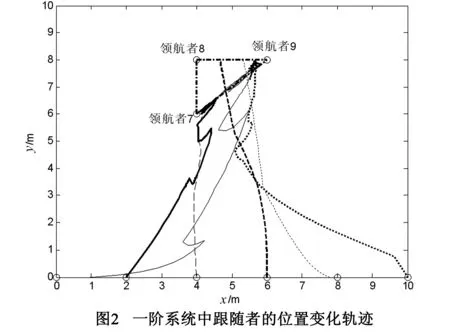
跟随者和领航者的初始位置分别取为x1(0)=(0,0),x2(0)=(2,0),x3(0)=(4,0),x4(0)=(6,0),x5(0)=(8,0),x6(0)=(10,0);x7(0)=(4,6),x8(0)=(4,8),x9(0)=(6,8).系统的运动轨迹如图2,可见各跟随者的位置最终渐近收敛到了由三个领航者的位置所围成的平面三角形区域内,即一阶多领航者网络化系统实现了群集运动.
5.2二阶网络化系统数值仿真
根据系统联合拓扑图G,得系统矩阵LF.经计算,LF的特征值约为:10.4630,4.7517,3.7539,2.2568,1.1940,0.5806.取β=1.0>0,γ=-0.2,α=2.1.跟随者的初始位置及初始速度分别取为q1(0)=(1,1),q2(0)=(2,2),q3(0)=(2,7),q4(0)=(3,5),q5(0)=(5,6), q6(0)=(7,3),p1(0)=(2,6),p2(0)=(3,8),p3(0)=(4,6),p4(0)=(5,5),p5(0)=(6,3),p6(0)=(9,7).静态领航者的初始位置取为q7(0)=(8,10),q8(0)=(10,8),q9(0)=(10,10).系统的运动轨迹如图3,可见各跟随者的位置最终渐近收敛到了由三个领航者的位置所围成的平面三角形区域内,即二阶多领航者网络化系统实现了群集运动.

6 结论
本文研究了在联合连通条件下具有多个静态领航者的网络化系统的群集运动问题,并分别针对一阶/二阶系统提出了相应的控制算法.运用控制理论及代数图论等理论工具分别对动态网络化系统进行了收敛性分析,给出了一阶系统的一般收敛性条件以及二阶系统收敛性对控制增益系数的约束条件.仿真示例分别对一阶系统和二阶系统的理论结果进行了有效验证.
[1]Lin P,Jia Y M.Average-consensus in networks of multi-agents with both switching topology and coupling time-delay[J].Physical A,2008,387(1):303-313.
[2]朱旭,闫建国,屈耀红.高阶多智能体系统的一致性分析[J].电子学报,2012,40(12):2466-2471.
Zhu Xu,Yan Jian-guo,Qu Yao-hong.Consensus analysis for high-order multi-agent systems[J].Acta Electronica Sinica,2012,40(12):2466-2471.(in Chinese)
[3]Dai P P,Liu C L,Liu F.Consensus problem of heterogeneous multi-agent systems with time delay under fixed and switching topologies[J].International Journal of Automation and Computing,2014,11(3):340-346.
[4]杨洪勇,田生文,张嗣瀛.具有领航者的时延多智能体系统的一致性[J].电子学报,2011,39(4):872-876.
Yang Hong-yong,Tian Sheng-wen,Zhang Si-ying.Consensus of multi-agent systems with heterogeneous delays and leader-following[J].Acta Electronica Sinica,2011,39(4):872-876.(in Chinese)
[5]杨洪勇,张玉玲,等.基于采样数据的时延多智能体系统的动态路径跟踪[J].电子学报,2013,41(9):1760-1764.Yang Hong-yong,Zhang Yu-ling,et al.Dynamic trajectory following of delayed multi-agent systems with sampling data[J].Acta Electronica Sinica,2013,41(9):1760-1764.(in Chinese)
[6]Hu A H,Cao J D,Hu M F.Consensus of leader-following multi-agent systems in time-varying networks via intermittent control[J].International Journal of Control,Automation and Systems,2014,12(5):969-976.
[7]Ji M,Ferrari-Trecate G,Egerstedt M,Buffa A.Containment control in mobile networks[J].IEEE Transactions on Automatic Control,2008,53(8):1972-1975.
[8]Hu J P,Yuan H W.Collective coordination of multi-agent systems guided by multiple leaders[J].Chinese Physics B,2009,18(9):3777-3782.
[9]Cao Y C,Ren W.Containment control with multiple stationary or dynamic leaders under a directed interaction graph[A].Proceedings of the IEEE Conference on Decision and Control[C].Piscataway:IEEE,2009.3014-3019.
[10]Ma Q,Miao G Y.Distributed containment control of linear multi-agent systems[J].Neurocomputing,2014,133(6):399-403.
[11]Liu H Y,Xie G M,Wang L.Necessary and sufficient conditions for containment control of networked multi-agent systems[J].Automatica,2012,48(7):1415-1422.
[12]Lou Y C,Hong Y G.Target containment control of multi-agent systems with random switching interconnection topologies[J].Automatica,2012,48(2):879-885.
[13]张安慧,陈健,等.二阶系统包容控制算法及其收敛速度分析[J].哈尔滨工业大学学报,2014,46(9):1-8.
Zhang An-hui,Chen Jian,et al.Containment control protocol and its convergence speed analysis for double-integrator dynamics systems[J].Journal of Harbin Institute of Technology,2014,46(9):1-8.
[14]Meng Z Y,Ren W,You Z.Distributed finite-time attitude containment control for multiple rigid bodies[J].Automatica,2010,46(12):2092-2099.
[15]Lin P,Jia Y M.Multi-agent consensus with diverse time-delays and jointly-connected topologies[J].Automatica,2011,47(4):848-856.
[16]Lin P,Jia Y M.Consensus of a class of second-order multi-agent systems with time-delay and jointly-connected topologies[J].IEEE Transactions on Automatic Control,2010,55(3):778-784.
[17]Qi B,Lou K,Miao S,Cui B T.Second-order consensus of leader-following multi-agent systems with jointly connected topologies and time-varying delays[J].Arabian Journal for Science and Engineering,2014,39(2):1431-1440.
[18]Xu W Y,Cao J D,et al.Leader-following consensus of non-linear multi-agent systems with jointly connected topology[J].IET Control Theory & Applications,2014,8(6):432-440.

王付永男,1990年3月出生,山东济南人.2013年于鲁东大学获得学士学位,现为鲁东大学硕士研究生,主要研究领域为复杂网络、多智能体编队控制等.
E-mail:wangfuyong0323@163.com

杨洪勇男,1967年9月出生,山东庆云人.2005年毕业于东南大学自动化系,获得博士学位,现为鲁东大学信息与电气工程学院教授,主要从事复杂网络、多智能体编队、智能控制、非线性系统控制等领域研究工作.
E-mail:hyyang@yeah.net
Flocking Motion of Dynamic Networked Systems with Multiple Leaders
WANG Fu-yong,YANG Hong-yong,HAN Fu-jun
(College of Information and Electrical Engineering,Ludong University,Yantai,Shandong 264025,China)
Control algorithms are presented for the first-order and second-order networked systems with multiple leaders and time-varying dynamic switching topologies.By applying modern control theory and algebraic graph theory,the cooperative motion of networked systems with jointly-connected topologies is studied,and the flocking motion control of networked systems is obtained,i.e.,trajectories of multi-agent systems are converged to the convex hull formed by multiple leaders.Through further researching the connected portion of networked systems,the constraint condition of flocking motion control for second-order networked systems is achieved.Finally,a simulation example is given to verify the effectiveness of the conclusion.
multiple leaders;networked systems;flocking motion;jointly-connected
2015-04-14;
2015-08-08;责任编辑:孙瑶
国家自然科学基金(No.61273152);山东省科技发展计划(No.2012YD03110)
TP27
A
0372-2112 (2016)07-1751-06
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.07.033

