原子钟两级驾驭算法及在建立GNSS时间基准中的应用
伍贻威,龚 航,朱祥维,刘文祥,欧 钢
(国防科技大学电子科学与工程学院,湖南长沙 410073)
原子钟两级驾驭算法及在建立GNSS时间基准中的应用
伍贻威,龚航,朱祥维,刘文祥,欧钢
(国防科技大学电子科学与工程学院,湖南长沙 410073)
本文提出了一种原子钟驾驭算法,方法是使用等价于Kalman滤波器加延迟器的数字锁相环(DPLL).本文完整地推导了DPLL的闭环系统传递函数和闭环误差传递函数,给出了其实现结构,和每次的对于被驾驭原子钟的调整量,并给出了使DPLL输出信号的频率稳定度最优的参数选取方法.在此基础上,提出了使用两个这样的DPLL级联起来的二级驾驭算法.理论分析和仿真实验都表明:该算法相比传统原子钟驾驭算法,参数选取更容易,可以保证输出信号的频率稳定度最优;并保证输出信号与第一级的参考输入保持时间同步.该两级驾驭算法可以应用于设计锁相振荡器,即先用铯钟驾驭氢钟,然后再驾驭数控振荡器(NCO);也可以应用于建立GNSS时间基准,即先用UTC(BSNC)驾驭产生BDT,然后再用BDT驾驭主控站主钟来产生BDT(MC).
原子钟驾驭;数字锁相环;Kalman滤波器;频率稳定度
1 引言
原子钟驾驭算法在建立守时实验室和全球导航卫星系统(GNSS)的时间基准中发挥着重要作用[1~4].以建立GNSS时间基准为例,其步骤可以分解为:① 获取观测钟差;② 使用时间尺度算法,综合地面站和星上的原子钟,建立一个纸面时间(单台钟或纸面时间都可以被视为一个时间尺度),即自由的“GNSST”;之所以打引号,是因为此时的GNSST是一个自由的时间尺度,还没有与UTC(k)保持时间同步;③ 使用驾驭算法,用UTC(k)驾驭自由的“GNSST”,得到GNSST;④ 使用驾驭算法,用GNSST驾驭主控站主钟,得到GNSST的物理实现,记为GNSST(MC),其中MC即master clock(主钟)的缩写.实际上,北斗、GPS等GNSS的时间基准的建立都可以用上述步骤来描述.
驾驭的目的:① 使被驾驭的时间尺度相对于用来驾驭的时间尺度之间的偏差尽可能小;② 使驾驭后生成的时间尺度的频率稳定度尽可能得到优化[3,4].
驾驭有两种实现形式:开环方式和闭环方式.开环方式的驾驭本质上是一个钟差预测算法[5,6].对于守时实验室,由于UTC是滞后的,所以只能通过预测纸面时间TA(k)或主钟相对于UTC的偏差,然后对主钟进行调整,从而生成UTC的本地实现,记为UTC(k).闭环方式的驾驭是通过反馈控制的方式来实现的,需要实时的观测值.此时,必须保证用于驾驭的时间基准是实时的,而不能像UTC那样是滞后的.
闭环方式的驾驭算法包括多种[1,2,7~11],例如:① 美国海军天文台(USNO)采用线性高斯二次型(Linear Gaussian Quadratic,LGQ)算法[1,2],用UTC(USNO)来驾驭自由的“GPST”(使用Kalman滤波器时间尺度算法,综合系统内多台原子钟而得到),得到受驾驭的纸面时间,即GPST;② GPS采用开关(Bang-Bang)控制[2]算法,用GPST驾驭GPS主控站的主钟,得到GPST的物理实现,记为GPST(MC).在这两个例子中,用于驾驭的时间基准UTC(USNO)和GPST,前者是物理时间,后者是纸面时间,但是都是实时的时间基准.
闭环方式和开环方式的驾驭算法本质上都要计算出对时间和频率的调整量.闭环方式的驾驭算法的一个优势在于:可以通过设计传递函数,同时考虑时间同步精度和频率稳定度的指标;而开环方式的驾驭(钟差预测)算法只能考虑时间同步精度的指标.
闭环方式的驾驭算法的设计难点在于参数的选取.参数的选取需要兼顾时间同步精度和频率稳定度,同时还要保证闭环控制系统是稳定的,因为参数选取不当会造成系统不稳定[8].然而,目前闭环方式的驾驭算法的研究不足在于:参数的选取一般都是针对某个具体应用,通过大量仿真后确定一组参数作为最优参数.可以说:这些方法具有普适性,但是参数却需要根据每次不同情况进行大量仿真后才能得到.
本文针对参数难以选取的问题,提出一种数字锁相环(DPLL)的闭环方式的驾驭算法,采用了一个等价于稳态Kalman滤波器加一个延迟器的DPLL.本文首先在Z域中推导了二状态变量Kalman滤波器的输入和输出之间的关系,发现Kalman滤波器进入稳态后,等价于一个标准的二阶2类DPLL;在文献[12,13]的基础上,完整地给出了DPLL的闭环系统传递函数和闭环误差传递函数;并证明在固定Kalman滤波器的过程噪声方差的情况下,该DPLL性能完全由观测噪声方差决定.由于Kalman滤波器的系统是完全可观测的[14],所以Kalman滤波器是稳定的.数值仿真验证了在加入延迟器后DPLL也是稳定的.于是在设计DPLL的过程中,不需要考虑系统的稳定性问题,只需要调整观测噪声方差,即可实现预期的驾驭效果.本文采用的策略是保证稳定度最优,并给出了从理论上(而不是仿真)确定参数的方法.该驾驭算法的参数选取方法相比传统DPLL具有明显优势.
本文进一步提出了两级驾驭算法.本文中以锁相振荡器有两路输入(1路为铯钟,1路为氢钟)为例进行说明.两级驾驭,即该锁相振荡器有两个DPLL.第一级DPLL用于通过铯钟驾驭氢钟,产生一个纸面时间.第二级DPLL用于通过该纸面时间驾驭数控振荡器(NCO).每个DPLL的驾驭策略依然是保证频率稳定度最优.最终两级驾驭生成的时间尺度综合了NCO的短期频率稳定度,氢钟的中长期频率稳定度,和铯钟的长期频率稳定度,并与第一级输入(铯钟)保持时间同步.仿真实验验证了两级驾驭算法的优异性能.本文最后描述了该两级驾驭算法在建立GNSS时间基准中的应用前景.
2 DPLL驾驭算法与性能分析
2.1算法原理
本节的目的是在Z域中推导给出二状态变量Kalman滤波器的输入和输出之间的关系;通过该表达式,给出等价于Kalman滤波器加延迟器的DPLL的闭环系统传递函数和闭环误差传递函数;在此基础上,给出该DPLL的实现结构图,和每次的控制量(对时间和频率的调整量)的表达式.
(1)系统的状态方程和观测方程
对于一个二状态变量的系统,其状态方程表示为:
(1)
其中,xk和yk为两个状态变量,T为采样间隔,uk为过程噪声.
观测方程表示为:
zk=xk+wk
(2)
其中,zk为观测量,wk为观测噪声.
这两个方程用矩阵的形式表示为:
(3)
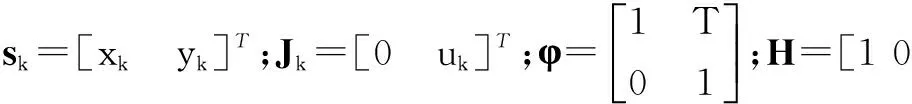
(2)Z域中稳态Kalman滤波器输入与输出之间的关系
Kalman滤波器可以用下面5个步骤进行描述[14]:
(4)
Pk,k-1=φ·Pk-1,k-1·φT+Q
(5)
(6)
(7)
Pk,k=(I-Kk·H)·Pk,k-1
(8)
其中,Kk是Kalman增益矩阵,Pk,k是估计误差矩阵,Pk,k-1是预测误差矩阵.
可以证明式(3)定义的系统是完全可观测的[14],因此Pk,k,Pk,k-1和Kk都收敛[14].把Pk,k、Pk,k-1和Kk的稳态值分别记为:Ps、Ps-和Ks.
由式(4)和式(7),当Kalman滤波器进入稳态时,有:
(9)
定义:
(10)
将式(10)代入式(9),得到:
(11)
其中,下标ij表示Ks矩阵中的第i行第j列的元素.
式(11)在Z域中表示为式(12):
(12)
由式(12)可以得到:
(13)
由式(12)和(13),式(10)在Z域中表示为:
V=Z-z-1·X-T·z-1·Y
=Z-X+Ks11·V
(14)
其中,Z代表zk的Z变换.
由式(14)得到:
(15)
定义:
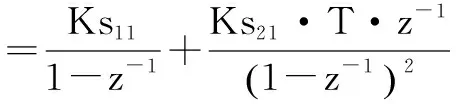
(16)
由式(13)、(15)和(16),得到式(17):
(17)
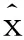
(3)DPLL的闭环系统传递函数和闭环误差传递函数
观察式(17),发现式(17)和二阶2类DPLL的闭环系统传递函数是相同的,于是,二状态变量Kalman滤波器等价于二阶2类DPLL[15].
为了使DPLL正常工作,在环路中加入一个延迟器z-1.该延迟器是必须的.因为,如果没有延迟器,当DPLL需要输出一个数值时,环路滤波器还没有计算出控制量.所以没有这个延迟器,DPLL是无法工作的.
由式(16)和(17),该DPLL的开环系统传递函数表示为式(18):
(18)
闭环系统传递函数表示为:
(19)
闭环误差传递函数表示为:
(20)
式(18)、(19)和(20)分别完整地给出了该等价于Kalman滤波器加延迟器的DPLL的开环系统传递函数、闭环系统传递函数和闭环误差传递函数.对比式(19)和(17),可以看见环路中引入了一个延迟.该DPLL的增益等价于稳态Kalman增益.这些结论进一步完善了文献[12,13]的研究成果.
本算法中,Kalman滤波器只是用于确定稳态Kalman增益Ks11和Ks21,并确定DPLL增益Ks11和Ks21.
式(19)和(20)可以看出,在T确定时,Ks11和Ks21完全决定了DPLL的性能.然而Ks11和Ks21完全是由过程噪声方差Q22和观测噪声方差R决定.所以,固定Q22=1s2不变,通过改变R的值,运行Kalman滤波器,就可以得到不同的(Ks11,Ks21),从而最终改变DPLL的性能.
该DPLL的优势在于:普通DPLL的增益有两个,选取参数并不容易,另外还需要考虑系统的稳定性问题;本文的DPLL的参数只有1个,即R,因此参数选取相对容易;另外,由于式(3)定义的系统是完全可观测的[14],所以Kalman滤波器是稳定的[14].由于该DPLL是Kalman滤波器加延迟器结构,大量的数值仿真表明加入延迟器后DPLL也是稳定的.
(4)DPLL的实现结构图和每次的驾驭量
由DPLL的开环系统传递函数,可以得到DPLL的实现结构.图1以用铯钟驾驭氢钟为例描述了DPLL的实现结构图.由图1得到:
Hmsteered(z)=G(z)·(Cs(z)-Hmsteered(z))+Hm(z)
(21)
其中,Cs代表铯钟,Hm代表氢钟,Hmsteered代表驾驭后的氢钟.
由式(21)得到式(22):
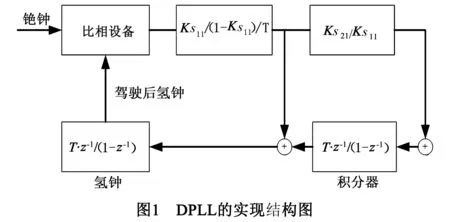
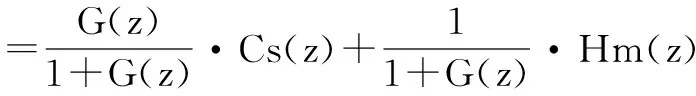
=H(z)·Cs(z)+He(z)·Hm(z)
(22)
由开环系统传递函数(18)和图1,得到在Z域中每次对于氢钟的时间的调整量(控制量)表示为
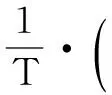
其中Err为驾驭误差,即铯钟和驾驭后氢钟的偏差Cs-Hmsteered.于是,驾驭后氢钟与氢钟的时差关系在时域中表示为式(23):
(23)
由式(23),每次对于氢钟的时间调整量为:
(24)
每次对于氢钟的频率调整量为:
(25)
最后需要指出的是,这里的DPLL是数学上的DPLL,而不是实际的物理上的DPLL,它的作用是为了计算出每次的控制量(时间和频率调整量).作为数学上的DPLL,只要获取了每次Cs-H之间的偏差,就可以通过传递函数自动计算出每次的控制量,通过反馈控制自动生成驾驭后的氢钟.驾驭的物理实现是通过相位微跃计来实现的.氢钟经过相位微跃计后的输出即为驾驭后氢钟.
2.2参数确定
第2.1节说明了在T已知时,DPLL的性能完全由R决定.驾驭算法需要兼顾驾驭误差和频率稳定度的性能.本文的策略是保证输出信号的频率稳定度最优.本节以用铯钟驾驭氢钟为例,说明如何调整R的值使DPLL输出信号的频率稳定度最优.
在频域中分析可以更清晰地展示不同的R值对于驾驭性能的影响.
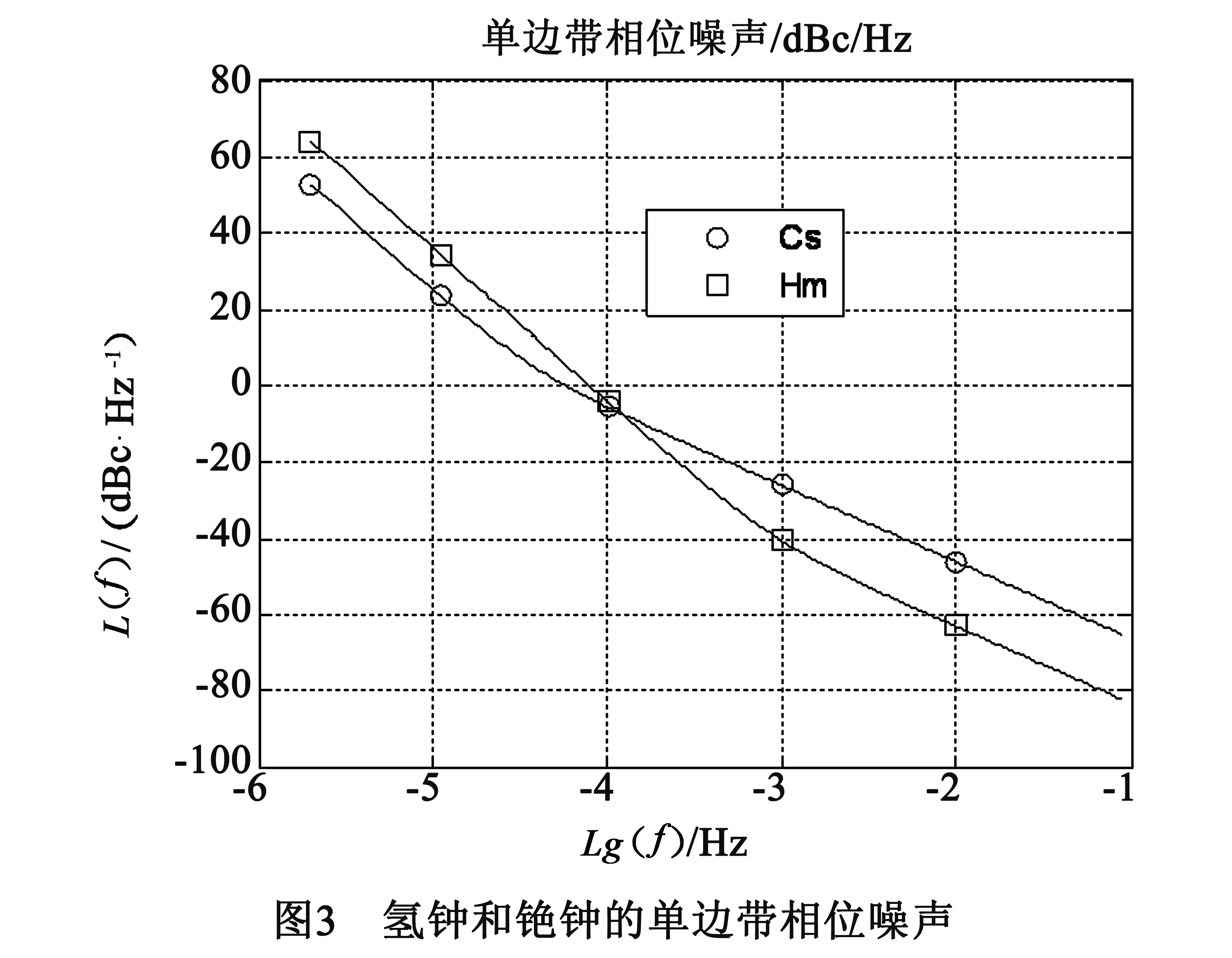
铯钟和氢钟的单边带相位噪声分别表示为[16]:
(26)
和
(27)
其中, f0是载波频率,h(Cs)i和h(Hm)i分别是铯钟和氢钟的噪声系数,i是幂律谱指数, f是边带频率.把它们交点的频率记为f′.
对于DPLL,可以使用近似变化z=ej2πf·T,得到一个近似的模拟锁相环(APLL).把z=ej2πf·T代入式(19)和(20),得到该APLL的闭环系统传递函数和误差传递函数为式(28)和(29).
(28)
(29)
显然,闭环系统传递函数(28)相当于一个低通滤波器,闭环误差传递函数(29)相当于一个高通滤波器,所以它们幅频响应曲线相交于一点.把交点的频率记为f″.本文的参数选取方法是调整R的值,使f″=f′.这时,DPLL输出信号充分综合了氢钟的中长期频率稳定度和铯钟的长期频率稳定度,频率稳定度达到了最优.
最终,由式(22),驾驭后氢钟的单边带相位噪声为:
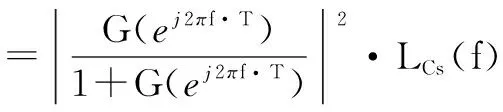
=|H(ej2πf·T)|2·LCs(f)
+|He(ej2πf·T)|2·LHm(f)
(30)
2.3仿真实验
仿真实验同样以用铯钟驾驭氢钟为例进行说明,步骤如下:
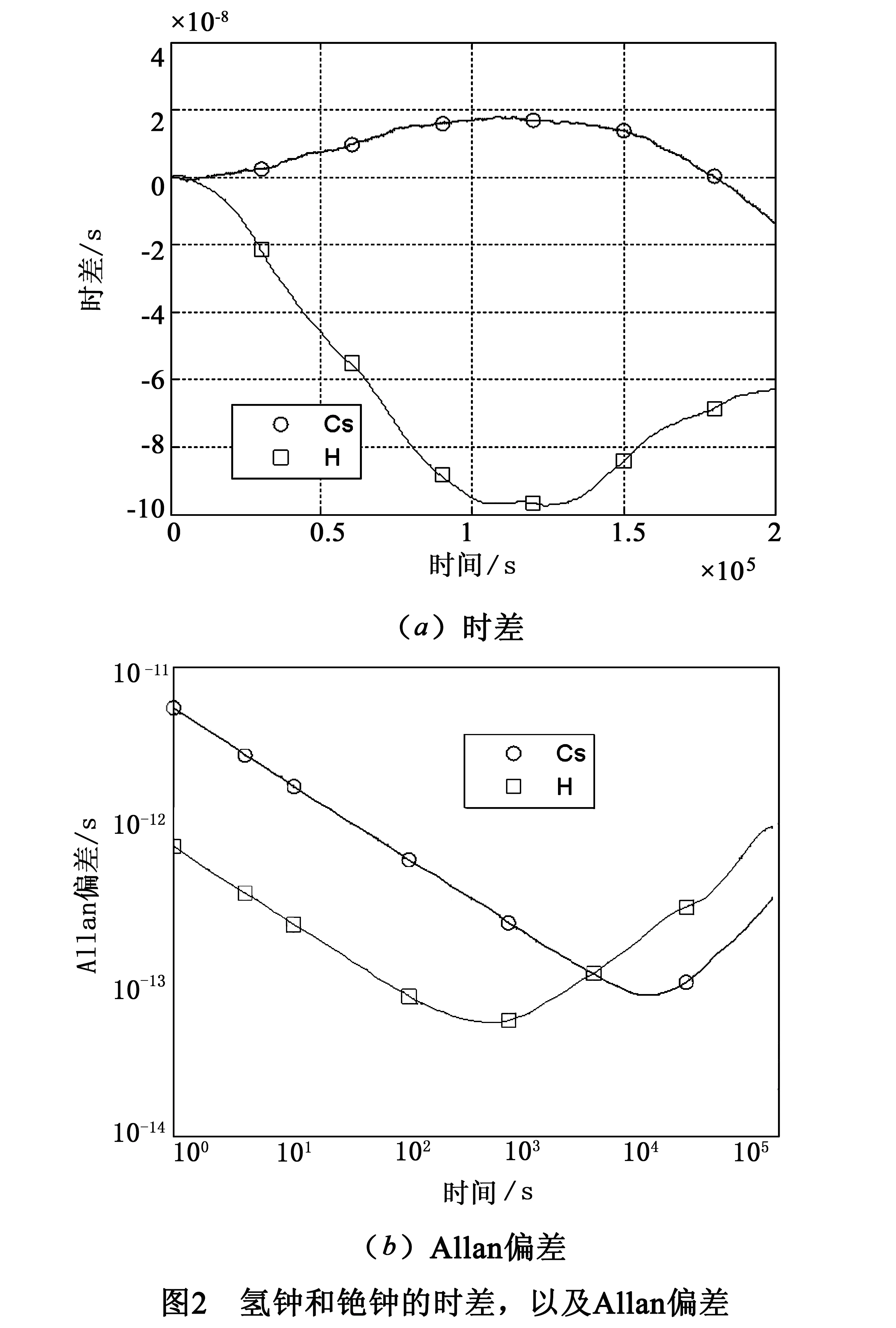
步骤1按照文献[17]的方法生成一台氢钟和一台铯钟.氢钟的参数为:h(Hm)0=1×10-24,h(Hm)-2=8×10-31.铯钟的参数为:h(Cs)0=5×10-23,h(Cs)-2=6×10-32.采样间隔T=1s.每台钟都含有200000个数据点.本文的目的是为了验证算法,所以氢钟和铯钟的确定性趋势项都设为零.图2描述了它们的时差,以及Allan偏差.需要说明的是:
①仿真氢钟和仿真铯钟的短期频率稳定度和真实的氢钟和铯钟相符,但是它们的长期频率稳定度明显差于真实的氢钟和铯钟.本文设置较大的噪声系数h(Hm)-2和h(Cs)-2,目的是为了在生成较少的数据点时(200000个数据点)就能看出驾驭效果.
②这里设置每隔1s对氢钟调整一次.实际上,在建立UTC(k)或GNSST中,一般是每隔3600s计算一次调整量;每隔1s对氢钟调整在实际上是做不到的,因为相位微跃计无法这么快速地调整;每隔1s对纸面时间或NCO调整是可以做到的,因为对纸面时间只需要在纸面上调整即可.这里只是通过仿真实验来验证算法,可以看成通过铯钟驾驭氢钟建立一个纸面时间.
步骤2设置氢钟和铯钟的载波频率为f0=10MHz.由式(26)和(27),作出氢钟和铯钟的单边带相位噪声曲线,发现f′大约为10-3.9Hz,如图3所示.
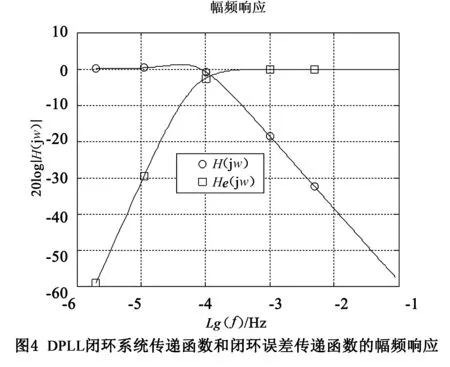
步骤3固定Q22=1s2不变,调整R的值,运行Kalman滤波器,得到Ks11和Ks21的值,由此得到了DPLL和APLL的传递函数.观察式(28)和(29)的交点频率f″.经过实验,发现当R′=2×10-14时,f″近似等于f′,如图4所示.于是,取R′=2×10-14.
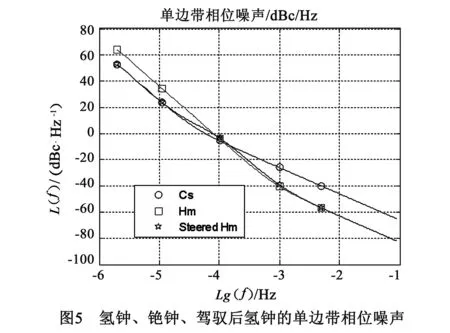
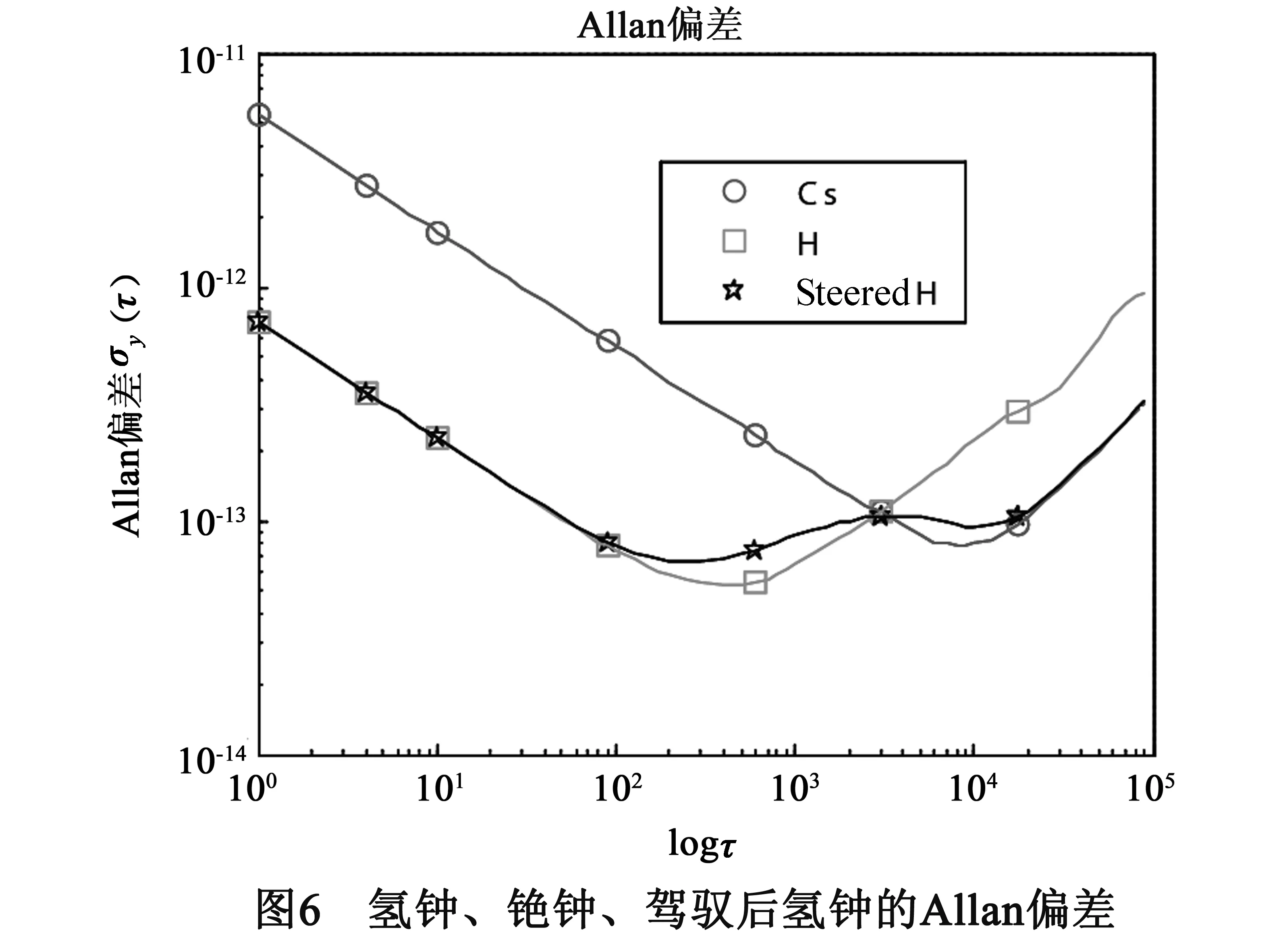

步骤4取R′=2×10-14对应的Ks11和Ks21,由式(30),在频域中得到了驾驭后氢钟的单边带相位噪声;由式(24)和(25),得到在时域中每次对于氢钟的调整量;在时域中对氢钟进行调整,得到了驾驭后氢钟,并计算得到驾驭后氢钟的Allan偏差.图5和图6分别描述了氢钟、铯钟和驾驭后氢钟的单边带相位噪声和Allan偏差.图7描述了它们的时差.图5和图6表明:驾驭后氢钟的频率稳定度综合了氢钟的中长期频率稳定度和铯钟的长期频率稳定度;从而验证了该方法可以使DPLL输出信号的频率稳定度最优.图7表明:驾驭后氢钟与铯钟保持了时间同步.综上,仿真实验验证了该驾驭算法的有效性.
3 两级DPLL驾驭算法与性能分析
目前的锁相振荡器一般只利用了一路参考输入[18].本文提出两级驾驭算法,可以改善这个不足.两级驾驭算法的核心思想是:当锁相振荡器有两路参考输入(其中一路为氢钟,一路为铯钟)时,其内部比相器可以获取氢钟、铯钟、和数控振荡器(NCO)两两之间的偏差;然后使用两个DPLL对NCO进行驾驭.其中,第一级DPLL用铯钟驾驭氢钟,建立一个纸面时间;然后第二级DPLL用该纸面时间驾驭NCO.从理论上分析,其输出信号将综合NCO的短期频率稳定度,氢钟的中长期频率稳定度,铯钟的长期频率稳定度,并且与第一级输入(铯钟)保持时间同步.相比传统锁相振荡器只利用了一路参考输入,该方法可以同时综合氢钟和铯钟的频率稳定度,具有明显优势.
算法原理如图8所示,其中G1(z)和G2(z)分别为两个DPLL的开环系统传递函数.对于其中每一个DPLL,参数选取的方法都和第2节的方法相同.

下面采用仿真实验来验证算法.
按照文献[17]的方法生成一个NCO,共含有200000个数据点,采样间隔T=1s.NCO的参数为:h(NCO)0=2×10-25,h(NCO)-2=5×10-30.氢钟和铯钟采用第2节相同的氢钟和铯钟.图9和图10分别描述了仿真NCO、氢钟、铯钟的时差和Allan偏差和单边带相位噪声.
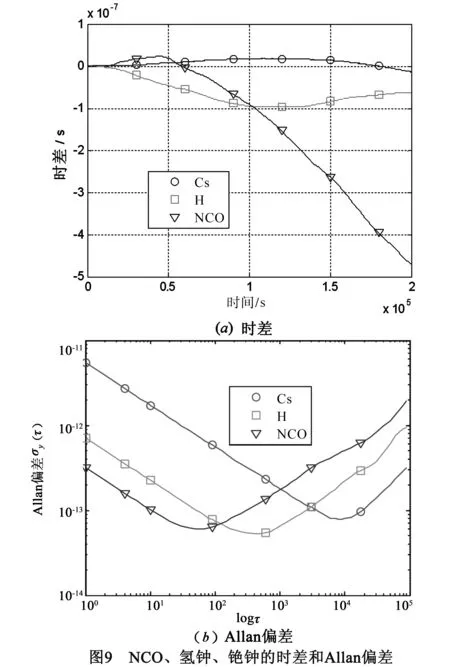
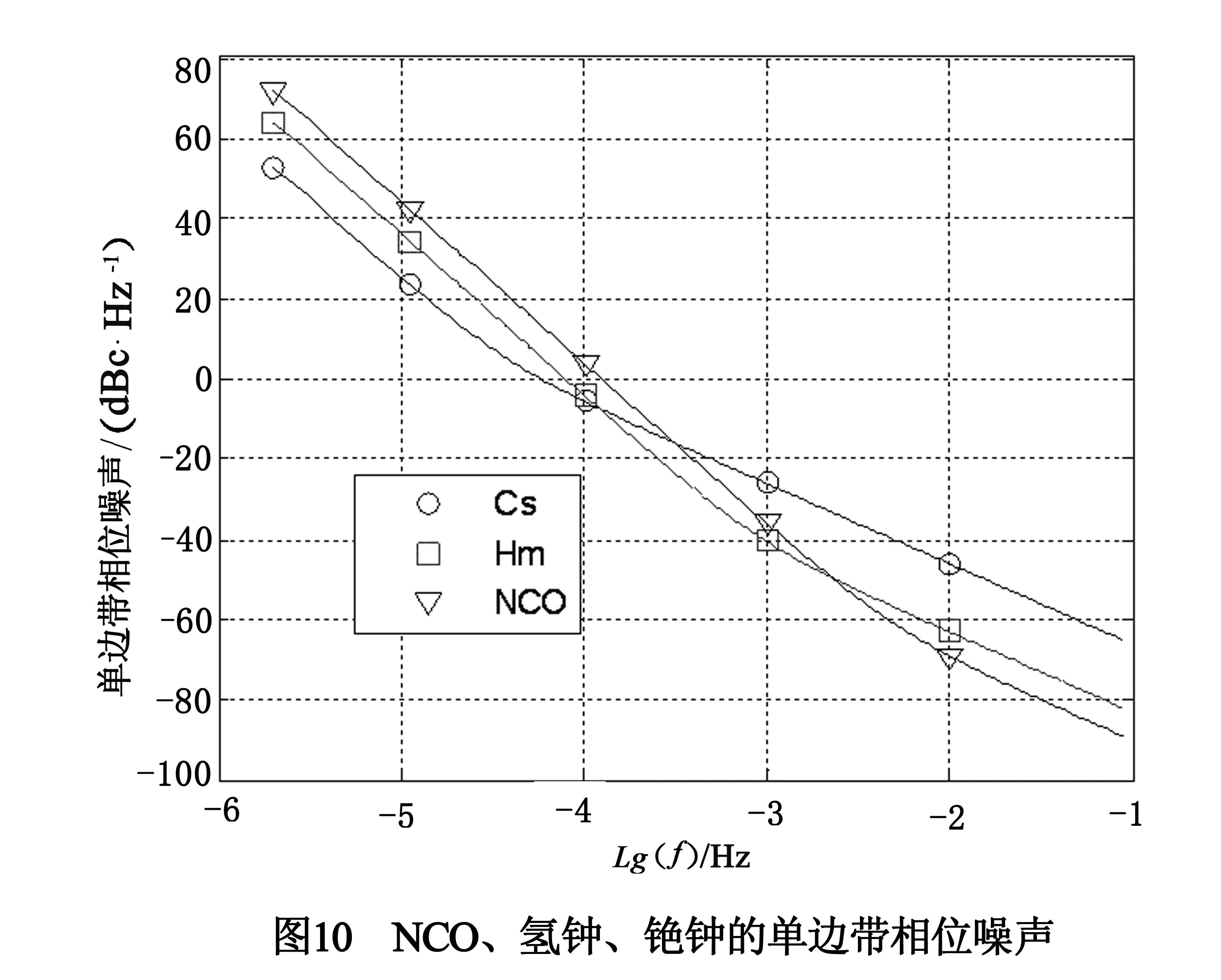

对于DPLL1,同样取R′=2×10-14.由图10可以看到,氢钟与NCO的单边带相位噪声曲线的交点频率约为10-2.64Hz.通过实验,发现当R′=1.6×10-9时,近似有f″=f′.所以,对于DPLL2,取R′=1.6×10-9.由式(24)和(25),计算得到每次DPLL1对于氢钟和DPLL2对于NCO的调整量,分别对氢钟和NCO进行调整,最终得到驾驭后的NCO,其时差和Allan偏差如图11所示.由图11看出,锁相振荡器的输出信号综合了NCO的短期频率稳定度,氢钟的中短期频率稳定度,铯钟的中长期频率稳定度,并且与第一级输入(铯钟)保持时间同步.综上,仿真实验验证了理论分析的结论.
4 算法在建立GNSS时间基准中的应用
本节以北斗卫星导航系统为例来描述两级驾驭算法在GNSS时间基准中的应用,实际上该算法可以推广应用到其它GNSS.北斗的系统时间记为BDT[19~21].建立BDT,首先需要使用时间尺度算法,综合系统内多台原子钟,建立一个纸面时间,即自由的“BDT”.该纸面时间相比单台原子钟,频率稳定度和可靠性更高.然后,使用两级驾驭算法,建立BDT和BDT(MC),其原理图如图12所示.其中,UTC(BSNC)是北京卫星导航中心(BSNC)维持的UTC的本地实现.

其中,第一级DPLL用于使用UTC(BSNC)驾驭自由的“BDT”,得到与UTC(BSNC)保持时间同步的BDT;第二级DPLL用于使用BDT驾驭主控站主钟,得到BDT的物理实现,记为BDT(MC).从图12中可以看出:这两个DPLL的传递函数是不同的,需要根据实际情况来选取合理的参数.
由于UTC(BSNC)可以看出是UTC的本地实现,可以认为“锁定”于UTC,所以和UTC一样,具有较高的长期频率稳定度;自由的“BDT”综合了多台地面站和星上的原子钟,因此具有较高的中长期频率稳定度;主控站主钟是一台主动型氢钟,具有较高的中短期频率稳定度.所以,UTC(BSNC),自由的“BDT”和主控站主钟分别相当于第3节中的铯钟、氢钟和NCO.最终使用二级驾驭算法得到的BDT和BDT(MC)都将与UTC(BSNC)保持时间同步;BDT将综合自由的“BDT”的中长期频率稳定度,和UTC(BSNC)的长期频率稳定度;而BDT(MC)将综合主控站主钟的中短期频率稳定度,自由的“BDT”的中长期频率稳定度,和UTC(BSNC)的长期频率稳定度.按照控制论,结合DPLL的传递函数,可以从理论上计算驾驭误差,即BDT和BDT(MC)相对于UTC(BSNC)的时间同步误差.
北斗主控站还可以与NTSC建立TWSTFT比对链路,UTC(NTSC)和UTC(BSNC)相互作为备份,使用两级驾驭算法,对自由的“BDT”和主控站主钟进行驾驭,进一步提升BDT的可靠性和长期频率稳定度.
最后需要指出的是,这里的DPLL是数学上的DPLL,而不是实际的物理上的DPLL,它的作用是为了计算出每次的控制量(调整量).作为数学上的DPLL,只要获取了每次UTC(BSNC)-BDT和BDT-BDT(MC)之间的偏差,就可以通过传递函数自动计算出每次的控制量,通过反馈控制自动产生BDT和BDT(MC).其中,对于第一级DPLL,计算出调整量后,只需要在数学上(纸面上)对BDT进行调整,因为BDT是一个纸面时间;而对于第二级DPLL,计算出调整量后,需要在物理上(一般是使用相位微跃计)对主钟进行调整.
5 结束语
本文提出了一种等价于Kalman滤波器加延迟器的DPLL驾驭算法;以及使用两个这样的DPLL级联起来的两级驾驭算法.本文从理论上推导了每个DPLL的闭环系统传递函数和闭环误差传递函数,证明DPLL的性能完全由观测噪声方差决定,并给出了调整观测误差方差的值使DPLL输出信号的频率稳定度最优的方法.仿真实验验证了该DPLL驾驭算法和二级DPLL驾驭算法的有效性.本文研究成果可以直接应用于设计锁相振荡器和建立GNSS时间基准.
[1]Paul Koppang,Robert Leland.Linear quadratic stochastic control of atomic hydrogen masers[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1999,46(3):517-522.
[2]Marcello Farina,Lorenzo Galleani,Patrizia Tavella,Sergio Bittanti.A control theory approach to clock steering techniques[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2010,57(10):2257-2270.
[3]Patrizia Tavella.Statistical and mathematical tools for atomic clocks[J].Metrologia,2008,45(6):183-192.
[4]Peter B Whibberley,John A Davis,Setnam L Shemar.Local representations of UTC in national laboratories[J]. Metrologia,2011,48(4):154-164.
[5]Panfilo G,Tavella P.Atomic clock prediction based on stochastic differential equations[J].Metrologia,2008,45(6):108-116.
[6]Wu Yiwei,et al.Uncertainty derivation and performance analyses of clock prediction based on mathematical model method[J].IEEE Transactions on Instrumentation and Measurement,2015,64(10):2792-2801.
[7]Marcello Farina,SergioBittanti,Patrizia Tavella,Lorenzo Galleani.Control of clock signals[J].Journal of the Franklin Institute,2009,346(5):449-469.
[8]Mbaye P M,Makdissi A,Plantard C,Vernotte F.Composite clock:A new algorithm for servoing a VCO firstly to a hydrogen maser clock and then to a caesium clock[J].Metrologia,2008,45(6):74-81.
[9]Plantard C,Mbaye P,Vernotte F.Composite clock including a cs clock,a h-maser clock,and a vco[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2010,57(3):707-713.
[10]李罡,吕晶,常江,李广侠.静态e用户精密授时问题的探讨[J].电子学报,2009,37(2):2243-2247.
Li Gang,Lü Jing,Chang Jiang,Li Guangxia.Discussion of precise time transfer of stationary user terminal[J].Acta Electronica Sinica,2009,37(2):2243-2247.(in Chinese)
[11]张杰,周栋明.GPS驯服中无偏滑动平均滤波算法的研究[J].电子学报,2013,41(2):413-416.
Zhang Jie,Zhou Dongming.Improved moving average filter for GPS disciplined[J].Acta Electronica Sinica,2013,41(2):413-416.(in Chinese)
[12]Peter F Driessen.DPLL bit synchronizer with rapid acquisition using adaptive Kalman filtering techniques[J].IEEE Transactions on Communication,1994,42(9):2673-2675.
[13]Ara Patapoutian.On phase-locked loops and Kalman filters[J].IEEE Transactions on Communication,1999,47(5):670-672.
[14]邓自立.卡尔曼滤波与维纳滤波——现代时间序列分析方法[M].哈尔滨:哈尔滨工业大学出版社,2001.
[15]Floyd M Garder.Phaselock Techniques (Third Edition)[M].USA:John Wiley & Sons,Inc,2005.
[16]Riley W J.Handbook of Frequency Stability Analysis[M].USA:NIST Special Publication 1065,2008.
[17]Kasdin N J.Discrete simulation of colored noise and stochastic processes and 1/f power law noise generation[J].Proceedings of the IEEE,1995,83(5):802-827.
[18]晏辉,张忠培.低信噪比下锁频锁相器性能分析及改进[J].电子学报,2011,39(1):1-6.
Yan Hui,Zhang Zhongpei.Performance analysis and improvement of phase and frequency detector at low SNR[J].Acta Electronica Sinica,2011,39(1):1-6.(in Chinese)
[19]吴海涛,李孝辉,卢晓春,华宇,杨旭海.卫星导航系统时间基础[M].北京:科学出版社,2011.
[20]Dong Shaowu,Wu Haitao,Li Xiaohui,Guo Shuren,Yang Qiangwen.The compass and its time reference system[J].Metrologia,2008,45 (6):S47-S50.
[21]Han Chunhao,Yang Yuanxi,Cai Zhiwu.BeiDou navigation satellite system and its time scales[J].Metrologia,2011,48(4):S213-S218.

伍贻威男,1987年出生于上海市,博士生.分别于2009年6月和2011年12月获得国防科技大学工学学士和工学硕士学位.主要研究方向为GNSS时间基准的建立与维持.到目前为止,以第一作者在IEEE Transactions on Instrumentation and Measurement和Metrologia等国际期刊上发表论文4篇.
E-mail:Yiwei-Wu-sh@126.com
龚航男,1984年出生于江苏徐州,博士、讲师.主要研究方向为原子钟与时间频率技术.
E-mail:gong-hang@163.com
朱祥维(通信作者)男,1980年出生于山东日照,博士、副研究员.主要研究方向为原子钟与时间频率技术,GNSS信号处理技术等.
E-mail:zhuxiangwei@nudt.edu.cn
刘文祥男,1981年出生于江西宜春,博士、副研究员.主要研究方向为卫星导航定位解算与完好性监测技术.
E-mail:liuwenxiang8888@163.com
欧钢男,1969年出生于湖南株洲,博士、教授、博士生导师.主要研究方向为GNSS信号处理、信息处理、接收机技术等.
E-mail:ougang1969@163.com
Twice Atomic Clock Steering Algorithm and Its Application in Forming a GNSS Time Reference
WU Yi-wei,GONG Hang,ZHU Xiang-wei,LIU Wen-xiang,OU Gang
(School of Electronic Science and Technology,National University of Defense Technology,Changsha,Hunan 410073,China)
An atomic clock steering algorithm is proposed by utilizing a DPLL equivalent to a Kalman filter with a delay.The close-loop system transfer function and the close-loop error transfer function are derived.The implement structure of the DPLL,and the adjustment to the atomic clock to be steered in each time are shown.A method for choosing the parameter such that the output frequency stability is optimal is also carried out.Then,a twice steering algorithm by means of two same DPLLs in the cascade form is proposed.The theoretical analyses and simulations all indicate that it is easier to choose parameters in the algorithm than the traditional algorithms,the output synchronizes to the first input and its frequency stability is optimal.The twice steering algorithm is useful for designing the phase-locked oscillator,where the number-controlled oscillator is first steered to a hydrogen maser and then steered to a cesium clock.The algorithm is also useful for forming a GNSS time.The method first steers BDT to UTC(BSNC),and then steers BDT(MC) to the steered BDT.
atomic clock steering;digital phase locked loop;Kalman filter;frequency stability
2015-05-19;
2015-12-14;责任编辑:孙瑶
TP228
A
0372-2112 (2016)07-1742-09
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.07.032

