基于智能方法的矢量控制变频调速系统仿真研究

江苏省徐州技师学院 陈 斌



基于智能方法的矢量控制变频调速系统仿真研究

江苏省徐州技师学院 陈 斌

【摘要】近年来，新兴的人工智能技术与矢量控制相结合的智能控制方法的研究取得了长足的发展，国内外对其研究和应用十分活跃。本文在介绍模糊控制的基础上，设计出模糊控制器并将其与矢量控制相结合，搭建出模糊控制器构成的矢量控制模型并进行仿真验证系统的可行性。

【关键词】异步电机；模糊控制；变频调速；仿真

1　模糊控制的基本原理

模糊的基本原理是1965年 美国加利福尼亚大学控制理论专家L.A.Zadeh教授在Information&Control杂志上发表了模糊集“Fuzzy Set”一文，首次提出了模糊集合的概念。用模糊集合（Fuzzy Set）来描述模糊事物的概念，很快为科技工作者所接受。

在许多情况下，被控对象由于其过程复杂，机理有不明之处，一些检测方法和检测装置无法进入被测模型，导致控制过程数学模型无法构建。因此用常规控制理论和控制方法去实现对这类对象的控制难以实现。假如把人的操作经验归纳成一系列的规则，存放在计算机中，利用模糊集理论将它定量化，使控制器模仿人的操作策略，这就是模糊控制器，采用模糊控制器构成的控制系统即模糊控制系统。

模糊控制相对于常规控制而言有以下优点：

（1）无须建数学模型，是解决不确定性系统的一种有效途径。（2）具有较强的鲁棒性，可用于非线性、时变、时滞系统的控制。（3）控制规则能进行分层联接，并且每条规则可以再延伸联接一个子规则库，这就可以组成多级控制。

2　模糊控制器设计

模糊控制器设计一般采用硬件和软件两种方法实现。在计算量较小时，模糊控制器的功能可采用软件设计实现，若到计算量较大并且实时性要求较高时，其功能可以通过采用硬件设备实现。模糊控制器设计的内容与步骤如下：

（1）模糊化

模糊化与反模糊化过程可看作为模糊规则与真实环境间的接口。一个实际值输入应表示为模糊集的形式，才能进行推理计算。而模糊输出集的信息应被转换为一个单值，这就是模糊推理系统的输出实值。模糊化就是采用一个模糊集表示实值信号的过程。

（2）模糊推理规则的建立

模糊规则表示为“if…then…”条件语句。更清楚的表示是，对多个变化条件的前提经推理产生一个决策结果。在应用中，通常将采用的模糊规则用模糊控制规则表的形式表示出来。模糊规则可以通过相关领域的专家给出，也可以通过大量的试验数据结出。无论应用哪种方法，得到的模糊规则都是近似的，因而还需要解决这些规则的协调问题。既要保证模糊规则的完备性，即对于任何模糊输入状态，都必须产生一个模糊控制器的输出，又要保证模糊规则的相容性问题，即模糊规则之间不能得到相互矛盾的结论。解决这两个问题，往往需要一定工程经验积累和试验数据。

（3）确定权与规则信度

明确地建立模糊规则的权和知识库中模糊规则信度之间的关系是相当重要的。例如，考虑规则置信矩阵是二位的，即对每一个输入集，只有一个规则的信度是非零，其值为1、这个限制意味着。权值只能是有限个值（模糊输出集的“中心”）中的一个。对每个模糊输入隶属函数，允许超过一个规则的可信度为有效，应用位于单位区间内的信度.允许相应的权去估计任何位于模糊输出集中的值。

（4）选择合适的推理合成算法与关系生成方法

设计模糊控制器需要选择适当的关系生成方法和推理合成算法。最常用的比较简便的方法是Mamdanl方法，模糊推理算法与模糊规则直接相关。它的复杂性依赖于模糊规则语句中模糊集的隶属函数的确定。选择一些简单的又能反映模糊推理结果的隶属函数可以大大简化模糊推理的计算过程。通常高斯隶属函数、梯形隶届函数和三角形隶届函数是使用最多的隶属函数。

（5）反模糊化

反模糊化就是压缩模糊输出集分布产生一个表达模糊系统输出的单值，然后再经过推理过程的输出。

3　模糊控制器组成的矢量控制变频调速仿真模型

Matlab软件中具有丰富的工具箱，其中的模糊逻辑工具箱Fuzzy Logic Toolbox用于建立模糊控制器，在Matlab软件命令窗口中输入fuzzy，即可进入模糊控制器编辑界面，然后根据控制要求构建一个二维的模糊控制器。模糊控制器中的e、ec、u ，分别代表输入量误差、误差变化量和输出控制量，它们都是的精确量且连续变化，所以应先将这些参数离散化。

如果［-n，n］是模糊子集的论域，［-x，x］为精确量的实际变化范围，Ke=n/x则为误差的量化因子，Kc=n/x为误差变化量化因子，Ku=x/n为输出控制量的比例因子。将e、ec、u划分为七个模糊子集并进行量化，｛正小（PS）、正中（PM）、正大（PB）、零（Z）、负大（NB）、负中（NM）、负小（NS）、｝分别表示语言变量，并确定其隶属度。然后将控制规则编组表达出专家的操作经验，最后采用模糊推理建立模糊查询表，这就把模糊控制器简化为查表运算。

［-150rad/s，150 rad/s］是转速误差的基本论域值，［-60rad/S2，60rad/S2］是其误差变化率的基本论域，作为输出控制量，基本论域 ［-200N.m，200 N.m］是输出控制量的转矩给定值，量化论域设定为［-5，5］，因此比例因子和量化因子分别为：

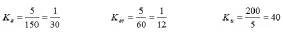
模糊控制器的输入为偏差及偏差变化，输出为转速估计增量。设模糊自适应信号的偏差、偏差变化的模糊变量分别为e，ec表示，输出为u（如图1）。

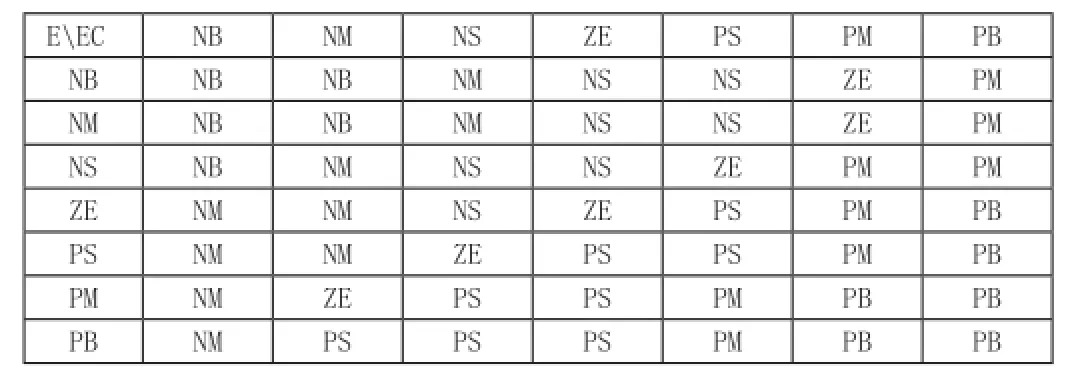
表1　模糊控制规则

图1　两输入一输出的模糊控制器结构

模糊语言值最终是通过隶属函数来描述的。隶属函数的形状越陡，分辨率就越高，控制灵敏度也较高；相反，隶属函数的变化率越缓慢，则控制特性也较平缓，系统的稳定性较好。选取各变量的隶属度函数如图2和图3所示。

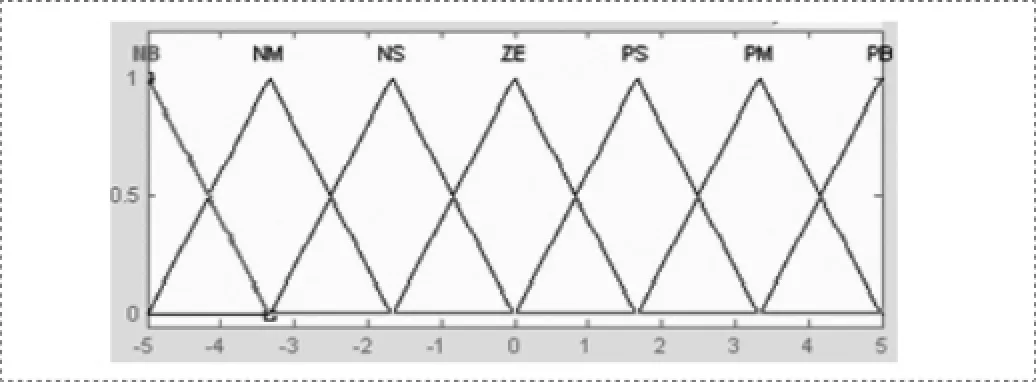
图2　输入变量e、de的隶属度函数

图3　输出变量Δω的隶属度函数

为了得到输出信号u，首先根据模糊的磁链误差e，ec，结合模糊规则以及重心法，转换成可识别信号，乘以合适的比例因子，从而得到最后的调节信号。输入、输出的各个模糊子集的隶属度函数控制规则如表1所示。

模糊控制器构成的矢量控制仿真模型如图4所示：

图4　模糊控制器构成的矢量控制变频调速仿真模型

4　仿真结果分析

图5　突加负载时电流、转矩、转速曲线

图6　突减负载时电流、转矩、转速曲线

从图5的结果可以看出：给定速度150rad/s，空载运行，转速上升需要0.5s时间，1.5s时加入200N·M扰动，转矩减小，转速几乎无变化，系统稳定性好。从图6的结果可以看出：给定速度150rad/s，恒转矩200N·M运转速上升需要1.3s时间，1.5s时突减200N·M扰动，转速几乎无变化，系统稳定性好。

图7　转速减少时电流、转矩、转速曲线

图8　转速增加时电流、转矩、转速曲线

从图7的结果可以看出：给定速度150rad/s，恒转矩200N·M运行，转速上升需要1.3s时间，在1.5S时电机速度由150 rad/s突减至100 rad/s，稳定时稳定时间为0.2s。

从图8的结果可以看出：给定速度100rad/s，恒转矩200N·M运行，转速上升需要0.8s时间，在1.5S时速度由100 rad/s突加至150 rad/s，稳定时间为0.5S，转速提升时间，跟随性好。

从以上仿真图形可以看出，从空载启动到稳定运行的过度时间为0.5秒，表明系统响应速度快，而且转速加速过程无超调量。因此在系统中加入模糊控制器后，系统在响应速度和稳定性等方面明显优于由PI控制器构成的矢量控制系统。

速度上升时间短，响应时间快，在加速的过程中速度无超调量，速度的跟随性、稳定性和动态误差等参数明显优于采用PI控制器的矢量控制系统。在1.5s时突加200N·M负载转矩时，转矩从零迅速突变为额定负载值之后保持不变，此时转速迅速下降，但在下降的过程中动态速降很小。由此可见，当负载改变时对系统的响应几乎无影响。仿真表明，在模糊控制下矢量控制变频调速系统转速上升时间比较快，达到稳定的时间比较短，无超调，调整时间短，对负载变化不敏感，具有较强的鲁棒性，明显优于PI控制器，达到了比较好的效果。

5　结论

本文首先介绍了模糊控制基本理论，模糊控制系统的组成和求解机理，然后将模糊控制与矢量理论相结合，设计出由模糊控制器构成的矢量控制变频调速模型，并在MATLAB/SIMULINK中进行了仿真实验。与由PI控制器构成的矢量控制模型相比，模糊矢量控制模型的稳定性，速度跟随性，抗扰动能力比前者要更好。

参考文献

［1］张国良.模糊控制及其Matlab应用［M］.西安：西安交通大学出版社，2003.16-28.

［2］孔凡才.自动控制原理与系统［M］.北京：机械工业出版社，2009：40-44.

［3］李辉.MATLAB/SIMULINK软件在电气工程类专业毕业设计教学环节中的应用［J］.电气电子教学学报，2003，25（1）：106-109.

作者简介：

陈斌（1980—），男，江苏徐州人，硕士研究生，江苏省徐州技师学院讲师，研究方向：交直流调速控制。