含忆阻模拟器的文氏振荡电路研究

南京邮电大学电子科学与工程学院 万江源 郑 洁 曾 进



含忆阻模拟器的文氏振荡电路研究

南京邮电大学电子科学与工程学院 万江源 郑 洁 曾 进

【摘要】忆阻器作为一种非易失性存储器和第四种电路基本无源元件，从它被提出时起就受到人们广泛关注。由于研制成本高和制造难度大，人们提出了一些动力学行为与忆阻器相似的忆阻模型。本文对忆阻模型的部分特性进行研究，采用简化的忆阻模拟器电路模型，进行分析，探究其伏安特性，并着重探究了含忆阻模拟器的文氏桥振荡电路频谱在不同条件下变化的基本特性，探索含忆阻的传统振荡电路特性改变及其在电子学当中的应用前景。

【关键词】忆阻模拟器；文氏桥；洄滞；频谱

1　引言

从电路理论出发，我们知道无源电路有三个基本元件：电阻、电容和电感，分别描述电压与电流的关系、电压与电荷的关系、电流与磁通量的关系，是目前实现电路的基本组成元件。同时，电路中有四个基本的参量：电流i、电压u、电荷q和磁通量，这四个基本参量两两之间具有六种关联：q和i通过电流电荷的基本定义联系起来（dq=idt），和u通过法拉第电磁感应定律联系起来（d=udt），u和i通过电阻的公理化定义联系起来（du=Rdi），u和q通过电容的定义联系起来（dq=Cdu），和i通过电感的定义联系起来（d和q之间没有通过相关物理定律或是物理模型联系起来［1］。

基于此，1971年美国加州大学伯克利分校的华裔科学家蔡少棠从电路基本变量的组合完备性出发，预言了忆阻器的存在［2］，并随后对忆阻系统相关特性进行了研究［3］。忆阻器其阻值受到之前的输入电压或电流的影响，有着类似神经网络中突触一样的功能或特性［4］。1976年，蔡少棠将忆阻的概念一般化，提出了新的概念—忆阻系统，即存在一类物理设备和系统，其特性类似忆阻器［1］。2008年5月，惠普公司实验室的Strukov等人首次在《自然》杂志上发表论文报道了忆阻器的实现［5］，并建立了忆阻元件的微分数学模型。

近年来，忆阻器为电路设计提供了全新的发展空间，这里既包括忆阻元件的电路建模、Spice宏建模、伏安特性分析，也包括含有忆阻元件的各种应用电路设计和系统特性的理论分析和数值仿真［6～8］。本文就忆阻器在振荡电路中的应用展开研究，振荡电路是一种常见电路，在相关技术领域中得到广泛地应用。在电子系统中，最常用的信号源是正弦波，而文氏桥振荡电路是一种重要且经典的正弦波RC振荡电路，其在测量、通信、无线电技术、自动控制和热加工等方面有着广泛的应用。本论文将应用仿真软件对忆阻系统的部分特性进行研究，提出相关忆阻器模拟电路模型，进行数学分析，探究忆阻器模型相关原理和特性，并进一步探究含忆阻器的传统文氏桥振荡电路的相关特性，以期摸索含忆阻条件下传统振荡电路特性改变或物理现象变化在电路理论中新的范例。=Ldi），但只有

2　忆阻器基本原理及模型

（1）式所表示的称为电荷控制型忆阻（也称流控忆阻），（2）式表示的称为磁通控制型忆阻（也称压控忆阻）。M与W分别称为忆阻与忆导。

图1　忆阻元件的基本模型（摘自文献［1］）

图1为惠普实验室给出的纳米级TiO2忆阻器的基本模型。该模型中，一片TiO2薄层和一片缺氧的二氧化钛薄层被两片铂电极夹在中间。其中，TiO2-x为掺杂区，TiO2为非掺杂区。在正向电场的作用下，掺杂区右边界会向非掺杂区移动，致使该结构掺杂区增大，电导率升高，电阻值变小，最终呈现导通状态（On）；在外加反向电压作用下，掺杂区电导率下降，电阻变大，最终呈现断开状态（Off）。即在外界电压或电流的作用下，掺杂区与非掺杂区之间的分割线会移动，两片铂电极之间区域的阻值会发生变化。

进一步分析，我们可得：

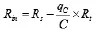
Rin被定义为输入电阻，Rs为起始输入电阻。式（4）中，在输入端有正向激励时，电阻在Rs基础上随着输入电流时间积分成比例增加，此忆阻模拟器可称为增加型忆阻模拟器。式（5）中，如果正向激励被作用增加型忆阻器极性相反的一端，则此忆阻模拟器便称为降低型忆阻模拟器。

上述两种忆阻模拟电路为一端接地型忆阻模拟电路，可以单独替代某些电路中部分电阻，改变电路相关特性。同时，它们还可以串并联或混联使用。除了一端接地型忆阻模拟电路外，还有浮地型忆阻模拟电路（忆阻模拟电路两端都不接地）［10］，在此，我们着重讨论上述两种一端接地型忆阻模拟电路在基本振荡电路（如文氏桥振荡电路）中进行电阻替换使用，忆阻器相关特性的对振荡电路的影响。

3　含忆阻模拟器的文氏桥振荡电路的特性分析

振荡电路应用非常广泛，其中RC振荡电路可以产生特定频率的正弦波，文氏桥振荡电路便是RC振荡电路中简单且经典的一种，其电路由两部分组成： 放大电路和选频网络。RC串并联选频网络接在运算放大器的输出端和同相输入端之间，构成正反馈；接在运算放大器的输出端和反相输入端之间的电阻，构成负反馈。正反馈电路和负反馈电路构成文氏电桥振荡电路。

我们首先分别分析上述增加型和降低型忆阻模拟器的基本特性，之后将其分别替换文氏桥振荡电路中相关电阻器件，研究引入忆阻模拟器用以替换电阻对文氏桥振荡电路振荡频率等特性的影响。通过仿真分析，我们得到增加型忆阻模拟器U-I关系具有斜体“8”字型的紧磁滞回线特性，这表明了忆阻模拟器的阻值会随着外界电压/电流的大小而改变，曲线上变化点的斜率的倒数便是阻值。并且，在不同频率下，磁滞回线表现不同，这是忆阻器的又一显著特性。

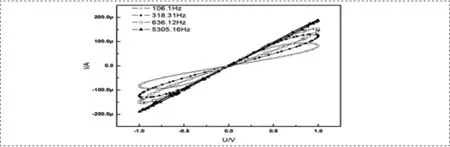
图2　增加型忆阻模拟器U-I关系图

图3　含忆阻模拟器的文氏桥振荡电路

如图2所示，我们得到了在不同频率下，增加型忆阻模拟器的磁滞回线图。可以发现，随着频率上升，洄滞行为明显减弱，大约在5kHz下，忆阻模拟器洄滞行为几乎消失。接着，我们着重探究用该忆阻模拟器替换文氏桥振荡器中的普通电阻R1，如图3所示。在不同振荡频率下，分析振荡电路的频率变化，研究其频谱结构。

图4　不同频率下含/不含增加型忆阻模拟器文氏桥振荡电路频谱图

经过分析，我们得到4组在不同频率下、含/不含忆阻模拟器文氏桥振荡电路频谱图，如图4所示。从图中我们可以看到，随着忆阻模拟器代入电路并替换普通电阻，文氏桥振荡电路频谱结构发生变化，即在主频区，含忆阻器的文氏桥振荡电路的频谱峰值幅度小于传统的不含忆阻器的文氏桥振荡电路的幅度。同时，尤其值得注意的是，在主峰频率2倍左右的频率区域，含忆阻器文氏桥振荡电路频谱会再次出现一较小的峰值。尤其在忆阻模拟器本身洄滞行为越明显时，含忆阻器的文氏桥振荡电路的频谱图中上述现象也更加明显。

图5　降低型忆阻模拟器U-I关系图

为了进一步研究不同类型忆阻器对振荡电路的影响，我们把降低型忆阻模拟器代入文氏桥振荡电路并对其相关特性进行了研究。同样，经过仿真分析，我们可以得到在不同频率下，降低型忆阻模拟器的磁滞回线图，如图5所示。我们将其代入文氏桥振荡电路用以替换普通电阻R1，进行分析得到在不同频率下其含/不含忆阻模拟器的频谱结构图，如图6所示。

图6　不同频率下含/不含降低型忆阻模拟器文氏桥振荡电路频谱图

从图中我们可以看到，其相关特性和代入增加型忆阻器后振荡电路所表现出类似。随着忆阻模拟器代入替换普通电阻，文氏桥振荡电路频谱结构同样发生变化，在主频区，含忆阻器的文氏桥振荡电路的频谱峰值幅度相比于传统的不含忆阻器的文氏桥振荡电路的幅度会稍微降低。同时，在主峰频率2倍左右的频率区域，含忆阻器文氏桥振荡电路频谱会再次出现一较小的峰值。尤其在忆阻模拟器本身洄滞行为越明显时，含忆阻器的文氏桥振荡电路的上述现象也更加明显。只是上述现象相对于引入增加型忆阻模拟器所产生的现象来说不是那么明显。

4　结束语

本文对忆阻器基本特性以及在振荡电路中的应用展开研究，这对于探究忆阻器在实际工作中的应用以及进一步分析忆阻器内部结构都具有重要的意义。本文中，我们采用了Hyongsuk Kim等人提出的忆阻模拟器模型，在此基础上，我们研究了该模型在文氏桥振荡电路中的应用，探究了引入忆阻模拟器后，传统文氏振荡电路相关特性变化，尤其是其频谱的改变。通过模型构建、电路仿真、数据采样、FFT变换作图分析，我们发现对于引入忆阻模拟器替换相关电阻后，含忆阻器文氏桥振荡电路的频谱会在主瓣峰值上略有降低，同时在主频率2倍频率处会出现新的较小的峰值。尤其在忆阻模拟器本身洄滞行为越明显时，含忆阻器的文氏桥振荡电路的上述现象也更加明显。由于忆阻器以及运算放大器本身的非线性特性，使得进一步分析具有一定复杂性。但这一与忆阻器有关的初步试验结论可能会对部分振荡电路、调频网络、敏感控制系统等电路的相关设计与分析工作产生一定程度的影响和起到部分借鉴作用。

参考文献

［1］王小平，沈轶，吴计生，孙军伟，李薇.忆阻及其应用研究综述［J］.自动化学报，2013，39（8）：1170-1184.

［2］Chua L O.Memrister-the missing circuit element［J］.IEEE Transactions on Circuit Theory，1971，18（5）：507-519.

［3］Chua L O and Kang S M.Memristive devices and systems［J］.Proccedings of the IEEE，1976，64（2）：209-223.

［4］Kim H，Sah M P，Yang C J，Cho S and Chua L O.Memristor Emulator for Memristor Circuit Applications［J］.IEEE Transactions on Circuits and Systems，2012，59（10）：2422-2431.

［5］包伯成，邹相，胡文，武花干.有源忆阻器伏安关系与有源忆阻电路频率特性研究［J］.电子学报，2013，41（3）：593-597.

［6］Benderli S and Wey T A.On SPICE macromodelling of TiO2 memristors［J］. Electron Lett，2009，45（7）：377-379.

［7］Loglekar Y N，Wolf S J.The elusive memristor：properties of basic electrical circuits［J］.Euro J Phys，2009，30（4）：661-675.

［8］Riaza R.Nondegeneracy conditions for active memristive circuits［J］.IEEE Trans Circuits and Systems II，2010，57（3）：223-227.

［9］Strukov D B，Snider G S，Stewart D R andWilliams R S.The missing memristor found［J］.Nature，2008，453：80-83.

［10］Yu D S，Iu H H C，Fitch A L，Liang Y.A Floating Memristor Emulator Based Relaxation Oscillator［J］.IEEE Transactions on Circuits and Systems，2014，61（10）：2888-2896.

作者简介：

万江源（1991—），男，安徽芜湖人，南京邮电大学硕士研究生，主要研究方向：物理电子。

Properties of Wien bridge oscillator circuit with Memristor Emulator

Jiangyuan Wan Jie Zheng Jin Zeng
（College of Electronic Science and Engineering；Nanjing University of Posts and Telecommunications；Nanjing China；210003）

Abstract：As a non-volatile memory and the fourth basic passive circuit component，memristor has attracted the public’s attention widely since it was proposed.Due to the high cost of development and complicated manufacture process，memristor emulator which shows the same dynamic behaviors as memristors was presented.In this paper，we investigated the properties of memristive system and adopted a simplified circuit model with memristor emulator.Most important，we investigated the properties of memristive Wien bridge oscillator circuit with memristor emulator，and explored its prospect of application in the electronics.

Keywords：memristor emulator；Wien bridge；hysteresis；frequency spectrum