基于多元线性回归分析的110 kV及以上电压等级变压器主材用量计算模型研究

刘平原, 张磊, 王宇, 谢鹏,, 卢启付, 廖嘉骏

(1. 南方电网有限责任公司物资部，广东 广州 510623；2. 华南理工大学 电力学院，广东 广州 510640；3.广东电网有限责任公司电力科学研究院，广东 广州 510080)



基于多元线性回归分析的110kV及以上电压等级变压器主材用量计算模型研究

刘平原1, 张磊2, 王宇3, 谢鹏1,2, 卢启付3, 廖嘉骏2

(1. 南方电网有限责任公司物资部，广东 广州 510623；2. 华南理工大学 电力学院，广东 广州 510640；3.广东电网有限责任公司电力科学研究院，广东 广州 510080)

为了更加准确地计算变压器有效材料(硅钢片及铜线)的成本，根据变压器主流供应商提供的历史数据，采用多元线性回归方法，确定影响原材料成本的主要性能参数。以空载损耗及负载损耗为输入量，硅钢片、铜线用量为输出量，建立不同电压等级、不同容量下的变压器原材料成本计算模型。通过对比容量增长定律法，更进一步验证计算方法及模型的适用性，为变压器采购成本管理提供有效的依据。

变压器；硅钢片及铜线；多元线性回归；空载损耗；负载损耗

根据IEC60300-3-3标准，对电力变压器的全生命周期成本(lifecyclecost，LCC)模型的主要构成要素进行具体分析。电力变压器从购置投入运行到报废退役，整个全生命周期过程的总成本包括四大成本之和，即一次投资成本、运行成本、中断供电损失成本以及报废成本[1-3]。关于变压器LCC建模的研究，国内外取得了一定的成果，但主要是针对成本动因及模型的构成进行完善及优化[4-7]，而对变压器制造成本的研究却很少。

变压器制造成本属于初始投资阶段成本，按照财务会计准则，其主要包括直接原材料成本、半构成品费用、直接人工成本、制造费用及期间费用[8-9]。文献[10-11]中指出直接原材料成本中硅钢片和铜线的成本占较大比例，根据变压器容量增长定律，随着变压器容量的增大，单位容量所消耗的有效材料将减少。当变压器电磁负载保持不变时，有效材料中的损耗与其重量成正比。文献[12]通过论述变压器铜铁(即铜导线和硅钢片)成本与空载损耗、负载损耗之间的关系，得出当变压器铜铁成本相等时总成本将最低的结论。国外研究学者利用人工神经网络、模糊逻辑等方法，基于变压器厂家提供的历史数据，以变压器额定容量、饱和磁通密度、最大电流密度、短路阻抗、安装高度、伏/匝及环境温度等各种参数为输入量，估算铝材、铁心、变压器油及铜线等变压器主材的重量，从而实现对变压器成本的分析[13-16]。目前，针对不同电压等级变压器主材重量的研究较少。

本文在上述研究成果的基础上，利用多重回归分析方法建立了110kV、220kV及500kV各电压等级下硅钢片及铜线用量的计算模型。在同一电压等级、同一容量、噪声及阻抗参数的条件下，以变压器空载损耗和负载损耗作为输入量，求取对应的变压器有效材料用量。结合实例，对比容量增长方法求取得到的结果，验证本文模型的准确性及合理性。所建立的变压器直接原材料成本计算模型能为制造成本管理提供有效的评判依据。

1　线性回归分析

1.1理论分析

本文尝试运用多元线性回归模型对变压器有效材料的用量进行预测分析。研究一个随机变量与一个(或几个)可控变量之间的相关关系的统计方法称为回归分析，而基于多个自变量的回归分析就叫做多元回归分析。当自变量与因变量之间存在线性关系时，称为多元线性回归分析[13-14]。多元线性回归的数学描述模型为：

(1)

式中：Y为因变量；x1、x2、…、xm为m个自变量；β0为常数项；βm为总体偏回归系数；ε为残差，即Y的变化中不能用现有自变量解释的部分。

1.2因变量与自变量的选取

变压器直接原材料成本主要包括硅钢片、铜线、绝缘油、钢材、绝缘材料等五大主材及辅助材料(含互感器、铜排、角环、引线电缆、密封件、包装材料等)。根据历史数据可知，五大主材中硅钢片及铜线成本比重分别占到20%、30%及以上，且其用量与变压器参数的关联性较强，更加具有研究意义。因此，选取硅钢片及铜线的用量作为因变量。若要保证变压器安全可靠运行，提高其技术经济指标，就需要考虑提高其性能参数，而这些性能指标与变压器材料的用量存在一定的关联，使得变压器的制造成本相应增加。变压器的主要性能参数包括容量、短路阻抗、负载损耗、空载损耗及声级水平等。根据空载损耗的工厂计算方法，空载损耗与铁心硅钢片总重量存在线性关系，而负载损耗中的电阻损耗与绕组上铜线的重量也存在类似的线性关系。为了更能反映变压器主材重量的变化情况，基于对现有文献及历史数据的分析，初步选取负载损耗和空载损耗作为自变量。

1.3多元线性回归检验

文献[17]指出，在求解回归方程之前必须解决Y与x1、x2、x3、…、xm之间是否存在线性关系，主要是检验m个回归系数β1、β2、…、βm是否全为0，全为0则认为线性关系不显著；若不全为0，则认为线性关系显著。只检验线性回归效果的显著性是不够的，还需要弄清楚每一个变量xi对Y的线性影响是不是重要的，即检验其回归系数βi是否为0，将次要的、影响不显著的变量剔除，重新建立只包含影响效果显著的回归方程。

1.3.1回归方程的显著性检验

回归方程的显著性检验旨在对模型中的被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断。因此可提出以下原假设与备择假设：

根据数理统计学理论，在原假设H0成立的条件下，统计量

(2)

该统计量服从自由度为(m，n-m-1)的F分布。其中n为独立样本的容量，SR为回归平方和，Se为剩余平方和或残差平方和。

依据样本值算得F的观测值F0，对于给定的显著水平α的检验法则为：若F0≥F1-α(m，n-m-1)，则拒绝H0，即认为Y与x1、x2、…、xm之间有显著的线性关系；若F0< F1-α(m，n-m-1)，则接受H0，即认为Y与x1、x2、…、xm之间不存在显著的线性关系[18]。

除此以外，还有p值检验法。如果pF>α，F0落入不能拒绝域，则不能拒绝H0；若pF<α，F0落入拒绝域，应拒绝H0。其中，pF=P{F>F0}，P为统计量F>F0的概率。

1.3.2变量的显著性检验

表2因变量与各自变量之间线性回归分析结果

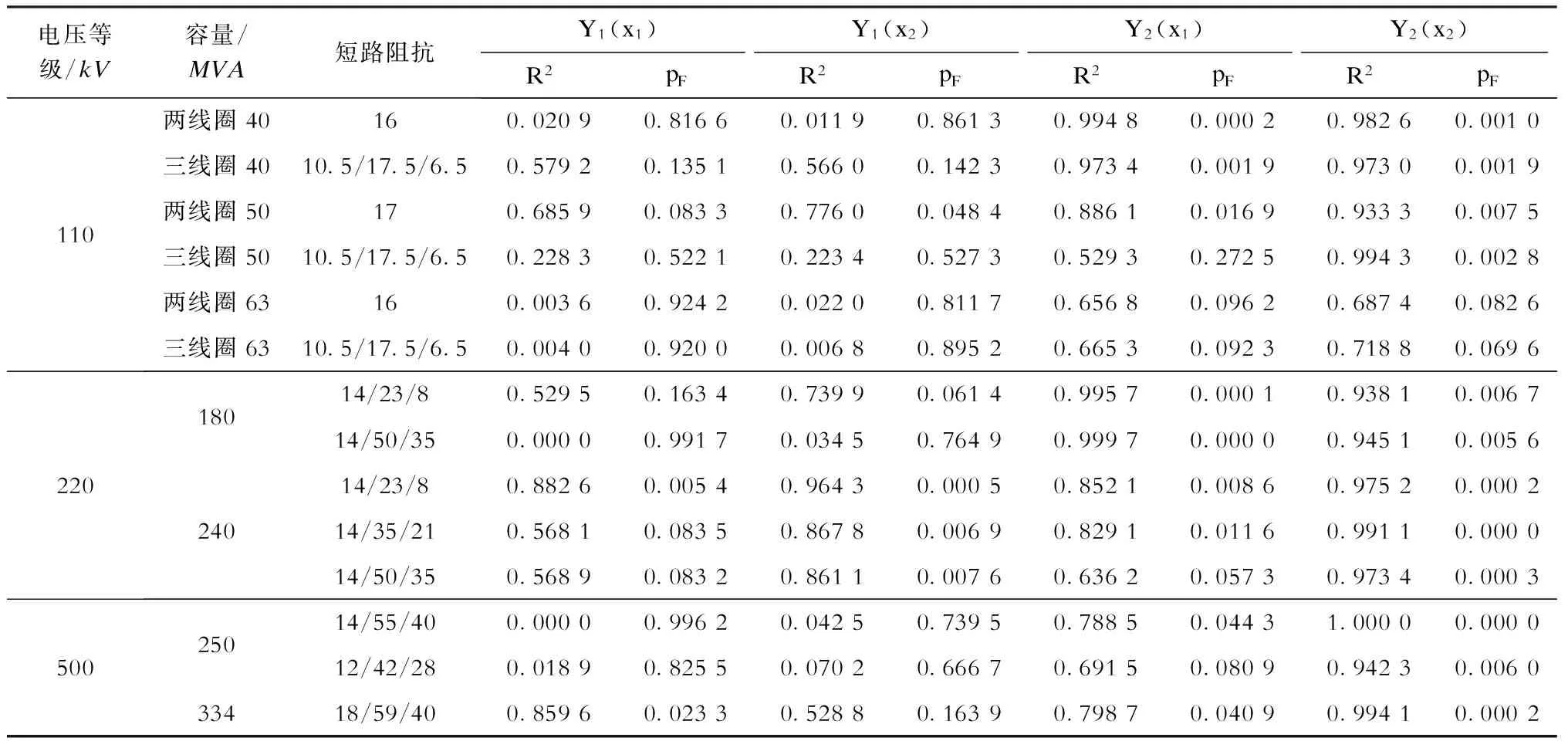
电压等级/kV容量/MVA短路阻抗Y1(x1)R2pFY1(x2)R2pFY2(x1)R2pFY2(x2)R2pF110两线圈40160.02090.81660.01190.86130.99480.00020.98260.0010三线圈4010.5/17.5/6.50.57920.13510.56600.14230.97340.00190.97300.0019两线圈50170.68590.08330.77600.04840.88610.01690.93330.0075三线圈5010.5/17.5/6.50.22830.52210.22340.52730.52930.27250.99430.0028两线圈63160.00360.92420.02200.81170.65680.09620.68740.0826三线圈6310.5/17.5/6.50.00400.92000.00680.89520.66530.09230.71880.069622018024014/23/80.52950.16340.73990.06140.99570.00010.93810.006714/50/350.00000.99170.03450.76490.99970.00000.94510.005614/23/80.88260.00540.96430.00050.85210.00860.97520.000214/35/210.56810.08350.86780.00690.82910.01160.99110.000014/50/350.56890.08320.86110.00760.63620.05730.97340.000350025033414/55/400.00000.99620.04250.73950.78850.04431.00000.000012/42/280.01890.82550.07020.66670.69150.08090.94230.006018/59/400.85960.02330.52880.16390.79870.04090.99410.0002

表3硅钢片用量与两自变量线性回归分析结果

电压等级/kV容量/MVA短路阻抗Y1(x1,x2)R2pFpt1pt2显著性检验(α=0.05)回归方程变量x1变量x2110两线圈40三线圈40两线圈50三线圈50两线圈63三线圈631610.5/17.5/6.51710.5/17.5/6.51610.5/17.5/6.50.28750.59870.77620.25510.09880.61650.71250.40130.22380.86310.90120.38350.47200.72600.97300.87100.72000.21700.47800.78500.46400.88100.69100.2160不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著22018024014/23/814/50/3514/23/814/35/2114/50/350.99400.75730.97860.89210.86420.00600.24270.00310.03540.05010.01200.13500.25000.47100.81000.00600.13000.03500.05800.0840显著不显著显著显著不显著显著不显著不显著不显著不显著显著不显著显著不显著不显著50025033414/55/4012/42/2818/59/400.20590.10880.94990.79410.89120.05010.54600.79600.05500.58700.69700.1980不显著不显著不显著不显著不显著不显著不显著不显著不显著

由于回归方程的总体线性关系显著不等同于每个解释变量对被解释变量的影响都是显著的，因此还必须对每个解释变量进行显著性检验，以决定是否作为解释变量被保留在模型中[19]。其原假设与备择假设为：

当H0为真时，统计量

(3)

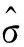
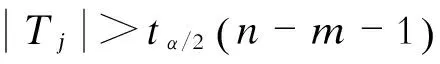
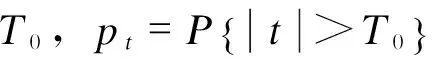
2　变压器直接原材料成本计算模型设计

2.1相关性分析

相关性分析是利用相关系数对变量间的线性关系进行分析，以数值的方式来反映两个变量间的相关密切程度[20]。相关系数的计算公式为

(4)

其中，n为样本容量，xi和yi为两变量对应的样本值，x、y分别表示它们所对应的样本均值。一般认为，当相关系数的绝对值大于0.8时，两变量间具有较强的线性关系；而相关系数的绝对值小于0.3时，两变量间的线性关系较弱。

根据某国产变压器厂所提供的历史数据，结合式(4)得到空载损耗与负载损耗两变量的相关系数见表1。由表1可以看出，14组变量的相关系数中有11组变量的相关系数都在0.8以上，而其他3组也接近0.8，说明这些变量之间存在严重的多重共线性，这对预测的结果将产生很大的误差，导致结论不正确[21]。因此将采用逐步回归的方法进行筛选，确定最后的自变量。

表1两变量相关系数

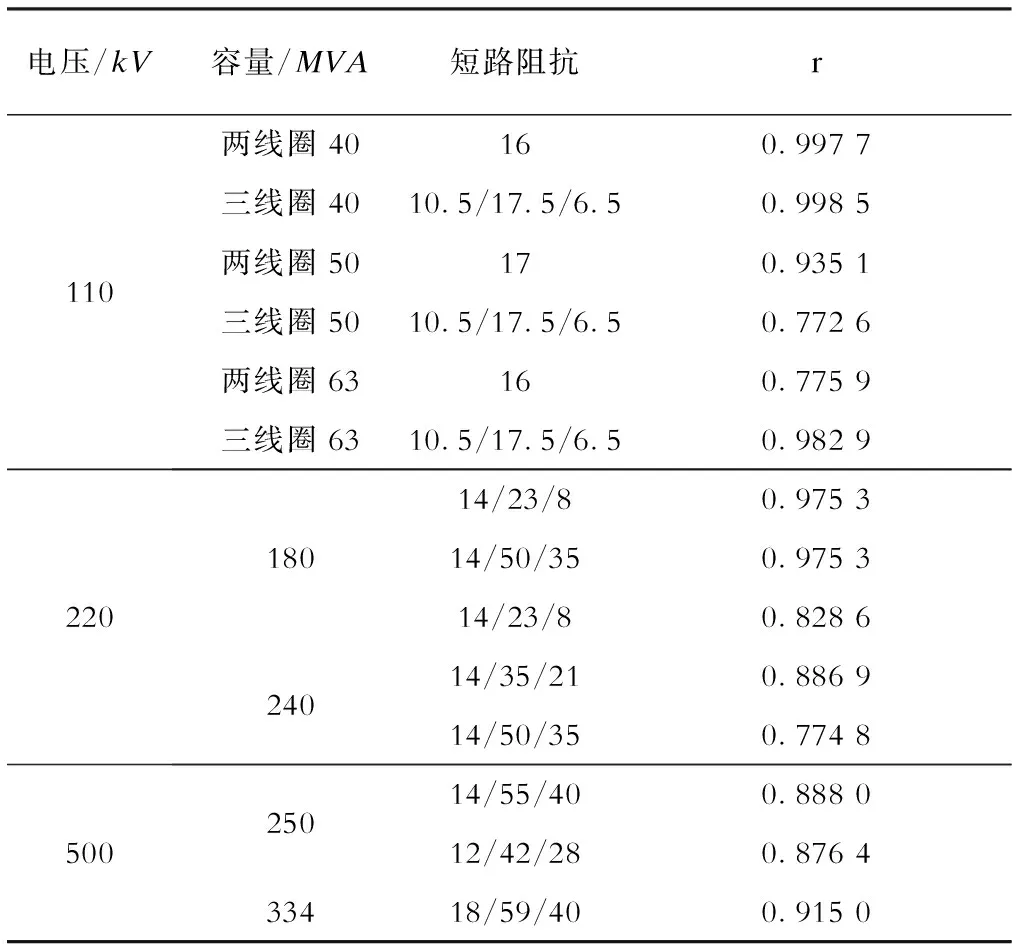
电压/kV容量/MVA短路阻抗r110两线圈40160.9977三线圈4010.5/17.5/6.50.9985两线圈50170.9351三线圈5010.5/17.5/6.50.7726两线圈63160.7759三线圈6310.5/17.5/6.50.982922018024014/23/80.975314/50/350.975314/23/80.828614/35/210.886914/50/350.774850025033414/55/400.888012/42/280.876418/59/400.9150

2.2逐步回归分析

本文通过某些已知的典型变压器常规参数，在不同的电压等级和不同的设计要求下拟合得出各自适用的数学公式。根据主流变压器厂所提供的变压器参数，在同一电压等级、同一容量、同一噪声和同一阻抗的条件下，针对不同参数条件下变压器中硅钢片用量(Y1)及铜线用量(Y2)，利用逐步回归法，对空载损耗(x1)、负载损耗(x2)两个自变量逐一选择，并对各变量及回归模型进行显著性分析，显著性水平α均取0.05，线性回归方程显著性分析结果分别见表2至表4。

以110kV电压等级、容量为40MVA、短路阻抗为16的变压器中硅钢片及铜线用量的线性回归为例，阐述线性回归的具体步骤。表2中，由拟合度参数R2大小可知，该参数条件下空载损耗对硅钢片用量的影响大于负载损耗对硅钢片用量的影响，但其拟合度系数R2也仅为0.020 9，且以空载损耗为自变量作一元线性回归，其pF为0.816 6(>0.05)，回归效果不显著，则可认为两个自变量不是影响硅钢片用量的主要因素。

同时，由表3的分析结果也可得出，两变量与硅钢片用量之间不存在显著的线性相关关系，线性回归计算模型无法成立。同理，如表2所示，该参数条件下空载损耗对铜线用量的影响大于负载损耗对铜线用量的影响，且以空载损耗为自变量作一元线性回归，其pF为0.000 2(<0.05)，回归效果显著，此时再引入负载损耗为自变量做二元线性回归。对新回归方程中的每个变量进行显著性检验，将在新的回归方程中不显著且对Y影响最小的自变量剔除，得到最优回归方程。表4中，空载损耗及负载损耗对应的pt分别为0.058及0.212。因此，虽然两变量都不能通过显著性检验，但空载损耗对铜线用量的线性影响较于负载损耗更为显著。此时应将负载损耗变量剔除，重新进行线性回归计算，即以空载损耗为自变量做一元线性回归，得到最终的线性回归方程。若二元线性回归方程中的每个变量都能通过显著性检验，则无需剔除自变量，此时二元线性回归方程即为最终计算模型。

2.3模型的建立

基于上述逐步回归分析的基本思想，根据变压器厂数据，进行多元线性回归求解，分别得到不同参数条件下硅钢片及铜线用量的线性回归方程。

表4铜线用量线性与两自变量线性回归分析结果

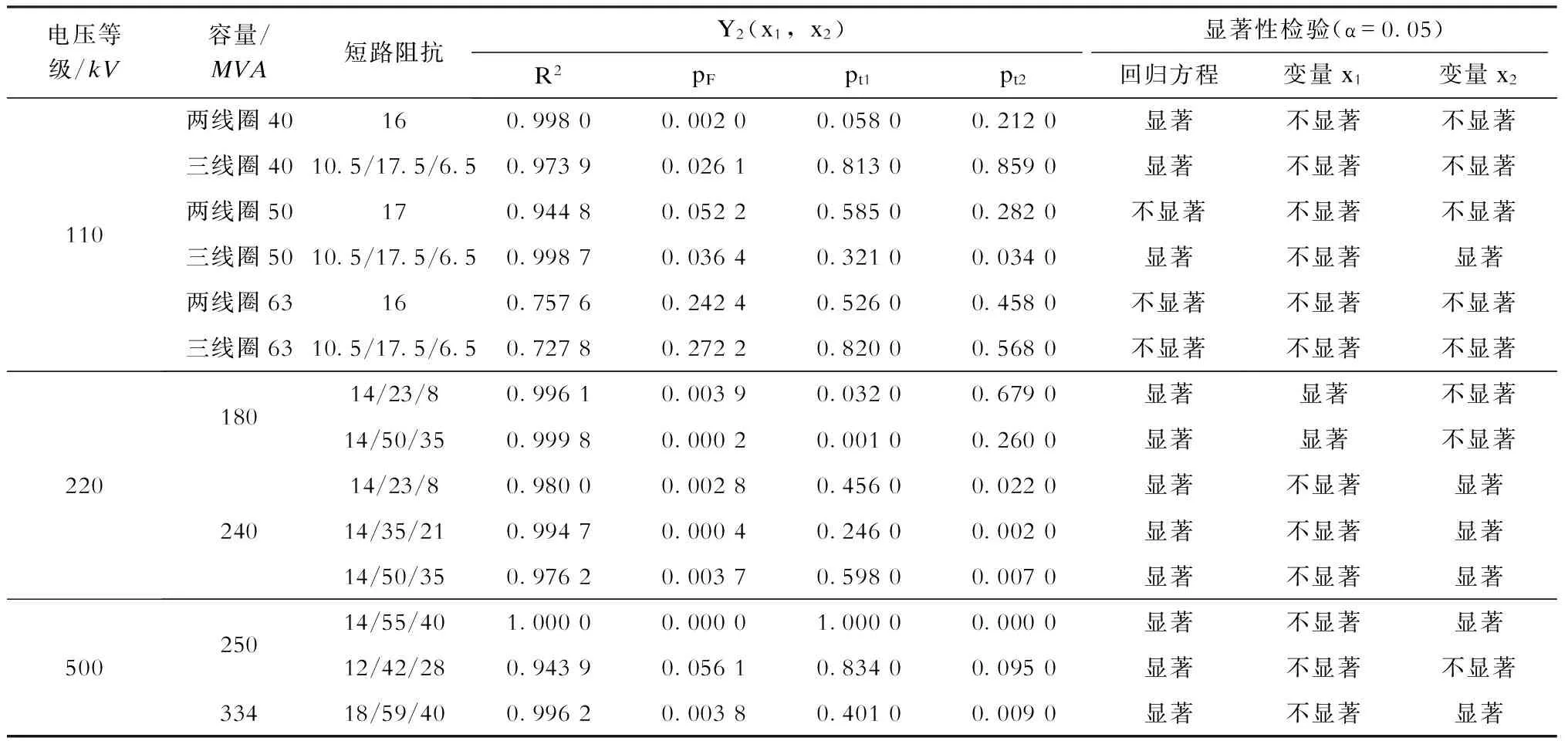
电压等级/kV容量/MVA短路阻抗Y2(x1,x2)R2pFpt1pt2显著性检验(α=0.05)回归方程变量x1变量x2110两线圈40三线圈40两线圈50三线圈50两线圈63三线圈631610.5/17.5/6.51710.5/17.5/6.51610.5/17.5/6.50.99800.97390.94480.99870.75760.72780.00200.02610.05220.03640.24240.27220.05800.81300.58500.32100.52600.82000.21200.85900.28200.03400.45800.5680显著显著不显著显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著不显著显著不显著不显著22018024014/23/814/50/3514/23/814/35/2114/50/350.99610.99980.98000.99470.97620.00390.00020.00280.00040.00370.03200.00100.45600.24600.59800.67900.26000.02200.00200.0070显著显著显著显著显著显著显著不显著不显著不显著不显著不显著显著显著显著50025033414/55/4012/42/2818/59/401.00000.94390.99620.00000.05610.00381.00000.83400.40100.00000.09500.0090显著显著显著不显著不显著不显著显著不显著显著

当电压等级为110kV，两线圈容量为40MVA，短路阻抗为10.5/17.5/6.5时，

Y2=17.083 6-0.202x1.

(5)

当电压等级为110 kV，三线圈容量为40 MVA，短路阻抗为16时，

Y2=15.231 9-0.152x2.

(6)

当电压等级为110kV，两线圈容量为50MVA，短路阻抗为17时，

(7)

当电压等级为110 kV，三线圈容量为50 MVA，短路阻抗为10.5/17.5/6.5时，

(8)

当电压等级为110kV，两线圈容量为63MVA，短路阻抗为10.5/17.5/6.5时，

Y2=33.290 2-0.084 9x2.

(9)

当电压等级为110 kV，三线圈容量为63 MVA，短路阻抗为16时，

(10)

当电压等级为220kV，容量为180MVA，短路阻抗为14/23/8时，

当电压等级为220 kV，容量为180 MVA，短路阻抗为14/50/35时，

Y2=75.79-0.398 1x1.

(12)

当电压等级为220kV，容量为240MVA，短路阻抗为14/23/8时，

(13)

当电压等级为220 kV，容量为240 MVA，短路阻抗为14/35/21时，

Y2=104.265 8-0.081 1x2.

(14)

当电压等级为220kV，容量为240MVA，短路阻抗为14/50/35时，

(15)

当电压等级为500 kV，容量为250 MVA，短路阻抗为14/55/40时，

(16)

当电压等级为500kV，容量为250MVA，短路阻抗为12/42/28时，

(17)

当电压等级为500 kV，容量为334 MVA，短路阻抗为18/59/40时，

(18)

由以上各计算模型可知，硅钢片用量与空载损耗及负载损耗之间并不完全能建立线性回归方程，在某些参数条件下无法获得硅钢片用量的计算模型，这与厂家所提供的数据存在较大的关系。由于该计算模型仅仅是针对厂商所提供的数据进行挖掘分析，并没有考虑变压器的设计原则、物理参数等方面对变压器材料用量的影响，因此该模型是变压器材料用量与空载损耗、负载损耗两变量之间数据上的数值关系，并不能完全说明变压器材料与空载损耗、负载损耗无关。

3　两种计算方法对比分析

3.1变压器容量增长定律

文献[6-7]指出在系列产品中，变压器的几何尺寸随变压器容量的增大而相应增加。如果几何尺寸之间的比例关系不变，变压器系列产品的结构都是相似的。其中，系列产品是指在变压器的设计原则、电压等级及其结构型式相同的情况下，在变压器容量等级之间相互构成数系的产品。由此可推导出铁心与铜线质量的计算公式如下。

铁心质量系列计算

(19)

式中：GT为任意容量变压器的铁心质量，kg；G1F为已知某一容量变压器的铁心硅钢片质量，kg；SN为要寻求的任意变压器容量，kVA；SN1为已知的变压器容量，kVA。

铜线质量系列计算

(20)

式中：GX为任意容量变压器的铜线质量，kg；G1M为已知某一容量变压器的铜线质量，kg。

变压器的容量增长定律基于变压器在设计原则、电压等级及结构型式相同的情况下，其几何尺寸随变压器容量的增加而相应增长，由此可计算出变压器单位容量所消耗的有效材料重量。而多元线性回归分析则是在电压等级、容量以及短路阻抗确定的情况下，利用已知的空载损耗与负载损耗，通过拟合公式计算出各主材的用量。

3.2计算结果对比

3.2.1实例1

以调研数据为例，取电压等级为110kV、容量为40MVA的双绕组变压器，其硅钢片和铜线的平均质量可取18.5t和10.5t，代入式(19)、(20)可得：

(21)

(22)

将SN=50代入式(21)、式(22)中可求得表5的结果。此即为利用容量增长定律计算得到的110 kV、容量为50 MVA的双绕组变压器的硅钢片及铜线的用量。同时，将电压等级为110 kV、容量同样为50 MVA、阻抗为17的变压器的损耗值代入其所对应的式(7)中，计算出硅钢片和铜线的用量，结果见表5。

表5容量增长定律与多重回归分析结果对比

计算方法硅钢片用量/t计算值实际值硅钢误差/%铜线用量/t计算值实际值铜线误差/%容量增长定律21.81235.1712.4111.39.82多重回归分析23.16230.7010.9911.32.74

由表5可以得出，多重回归模型的计算结果相较于容量增长定律的计算结果误差较小，且硅钢片用量的计算值更加接近实际值，误差均不超过1%。

3.2.2实例2

以调研数据为例，电压等级为220 kV、容量为240 MVA的变压器，硅钢片和铜线平均重量分别为84.61 t和42.38 t，代入式(19)、(20)可得：

(23)

(24)

将SN=180代入式(23)、式(24)中，可求得表6的结果。取电压等级为220kV，容量同样为180MVA，阻抗为14/23/8的变压器，将不同空载损耗负载损耗值代入式(11)中，计算得到硅钢片和铜线的用量，结果见表6。

由表6可以看出，该变压器参数条件下，硅钢片及铜线用量利用多重回归模型的计算结果相较于容量增长定律的误差较小，其最大误差分别为7.09%、8%。

表6容量增长定律与多重回归分析结果对比

计算方法硅钢片用量/t计算值实际值硅钢误差/%铜线用量/t计算值实际值铜线误差/%容量增长定律89.63873.0243.907138.16多重回归分析87.26870.3070.30710.99

3.2.3实例3

以调研数据为例，电压等级为500kV、容量为250MVA的变压器，硅钢片和铜线平均重量分别为75.2t和27.2t，代入式(19)、(20)可得：

(25)

(26)

将SN=334代入式(25)、式(26)中，可求得表7的结果。取电压等级为500 kV，容量同样为330 MVA，阻抗为14/55/40的变压器，将空载损耗、负载损耗代入式(17)中，计算得到硅钢片和铜线的用量。两种方法求得的电压等级为500 kV、容量为250 MVA的变压器的硅钢片与铜线用量分别见表7。

表7容量增长定律与多重回归分析结果对比

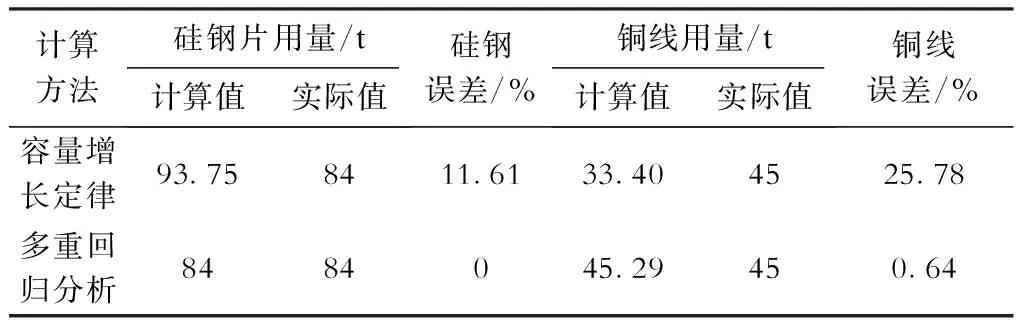
计算方法硅钢片用量/t计算值实际值硅钢误差/%铜线用量/t计算值实际值铜线误差/%容量增长定律93.758411.6133.404525.78多重回归分析8484045.29450.64

由表7可以看出，多重回归模型的计算结果相较于容量增长定律的误差较小，均不超过3%。而铜线用量运用两种计算方法的结果误差波动性较大。

3.3结果差异性分析

由以上3个实例可以看出，对于硅钢片或铜线的用量，相较于容量增长定律的计算结果，利用多元线性回归模型计算结果更接近实际用量。而在实例2、3中，在不同空、负载条件下利用两种方法所得铜线用量的计算值与实际值的偏差波动性较大，且有几组误差均超过10%。产生这种现象的原因主要是：一方面由于目前模型计算及检验所提供的数据较少，且空、负载原始数据选取相差不明显，对多重回归模型的准确度造成一定的影响；另一方面与变压器厂家的生产设计有关，由于特殊结构要求，造成同一系列变压器的重量、尺寸及损耗关系与增长定律有些出入，而实际硅钢片及铜线的用量通常为满足设计要求都留有适当裕度，能够满足某一范围内的空、负载值。由于容量增长定律法仅利用了已知容量和已知材料用量这两种参数，而不同阻抗下同一容量、同一主材的用量也会有所差异，因此容量增长定律并不能全面反映各参数对变压器材料用量的影响。总体来说，利用多元线性回归模型计算变压器有效材料(硅钢片及铜线)的重量更加具有针对性和有效性。

4　结束语

本文结合厂家提供的数据，利用多元线性回归分析方法，建立了各电压等级不同参数下变压器有效材料用量与负载损耗及空载损耗之间的关系。利用逐步回归法，对空载损耗和负载损耗两个自变量进行逐一检验，得到符合要求的线性回归方程。同时，根据厂家所提供的数据来比较容量增长定律与回归分析两种方法计算方法与结果的异同。由两种方法计算结果的比较可以看出，回归分析方法在考虑了较全面的参数影响后，其计算误差要比容量增长定律法的误差明显要小得多，而且误差在材料不同时也有所不同，两种方法下硅钢片的误差基本上均小于铜线的误差，这可能与变压器自身的生产设计相关。综上所述，依据本文所提出的利用多元线性回归分析法建立的变压器有效材料用量计算模型更具有实用性和可靠性。

[1] 徐玉琴，任正，詹翔灵，等.电力变压器全寿命周期成本建模及其综合敏感性分析[J].华北电力大学学报，2014，41(6)：80-87.

XU Yuqin, REN Zheng, ZHAN Xiangling, et al. Life Cycle Cost Model and Comprehensive Sensitivity Analysis of Power Transformer[J]. Journal of North China Electric Power University, 2014,41(6):80-87.

[2] 唐维，陈芨熙，王子龙，等.基于不完整数据的变压器全生命周期成本[J].浙江大学学报(工学版)，2014，48(1)：42-49.TANG Wei, CHEN Jixi,WANG Zilong, et al. Life Cycle Cost Assessment for Transformer Based on Incomplete Records[J].Journal of Zhejiang University(Engineering Science),2014,48(1):42-49.

[3] 魏勇，王锐. 全数字化变电站二次系统的全生命周期成本管理分析[J]. 电力系统保护与控制，2010,38(4)：78-83,87.

WEI Yong,WANG Rui.Brief Analysis of Total Life Cycle Costs Management of Secondary System of Digital Substation[J].Power System Protection and Control,2010,38(4):78-83,87.

[4] NILSSON J, BERTLING L. Maintenance Management of Wind Power Systems Using Condition Monitoring Systems Life Cycle Cost Analysis for Two Case Studies[J].IEEE Trans. on Energy Conversion, 2007, 22 (1): 223-229.

[5] MEYER C, DE DONCKER R W. LCC Analysis of Different Resonant Circuits and Solid-state Circuit Breakers for Medium-voltage Grids[J]. IEEE Trans. on Power Delivery, 2006,21(3):1414-1420.

[6] AMOIRALIS E I, TSILI M A, GEORGILAKIS P S, et al. Energy Efficient Transformer Selection Implementing Life Cycle Costs and Environmental Externalities[C]//The 9th International Conference, Electrical Power Quality and Utilization, Barcolona:[s.n.],2007.

[7] POLITANO D, FROHLICH K. Calculation of Stress-dependent Life Cycle Costs of a Substation Subsystem, Demonstrated for Controlled Eenergization of Unloaded Power Transformers[J]. IEEE Trans. on Power Delivery, 2006,21(4): 2032-2038.

[8] 刘有为，马麟，吴立远，等.电力变压器经济寿命模型及应用实例[J].电网技术，2012，36(10)：235-240.

LIU Youwei, MA Lin, WU Liyuan, et al. Economic Life Model Of Power Transformer and Its Application[J].Power System Technology, 2012, 36(10):235-240.

[9] 史雪飞，赵彪，郑燕，等.基于参数可测的交流变压器制造成本估算模型[J].电力建设，2013，34(5)：11-16.

SHI Xuefei, ZHAO Biao, ZHENG Yan, et al. Manufacturing Cost Estimation Model of AC Transformer Based on Measurable Parameters[J]. Electric Power Construction,2013,34(5):11-16.

[10] 路长柏.电力变压器计算[M].哈尔滨:黑龙江科学技术出版社，1986.

[11] 谢毓城.电力变压器手册[M].北京：机械工业出版社，2003.

[12] 王德江.变压器铜铁成本优化分析及应用[J].变压器，1995(9)：26-28.

WANG Dejiang. Analysis and Application on Copper and Iron Cost Optimization of Transformer[J]. Transformer,1995(9):26-28.

[13] MALIK H, JARIAL R K. Fuzzy-logic Applications in Cost Analysis of Transformer’s Main Material Weight[C]//2011 International Conference on Computational Intelligence and Communication Networks (CICN).Gwalior, India:IEEE, 2011.[14] MEHTA H D, PATELl R M, TRIVEDI P H. Cost Estimation of Transformer Main Materials Using Artificial Neural Networks[C]//2012 Nirma University International Conference on Engineering (NUiCONE). Ahmedabad,India: IEEE,2012.

[15] YADAV A K, SINGH A, MALIK H, et al. Cost Analysis of Transformer’s Main Material Weight with Artificial Neural Network (ANN)[C]//2011 International Conference on Communication Systems and Network Technologies (CSNT).Katra, Jammu:IEEE, 2011.

[16] FIROUZFAR M, SALAHh P, MADAHI S S K. Estimating the Weight of Main Material for 63/20 kV Transformers with Artificial Neural Network (ANN)[C]//2010 4th International Power Engineering and Optimization Conference (PEOCO). Shah Alam,Malaysia: IEEE, 2010.

[17] 田兵.多元线性回归分析及其实际应用[J].阴山学刊(自然科学版)，2011，25(1)：16-19.

TIAN Bing. Multiple Linear Regression Analysis and Its Practical Applications[J].Yinshan Academic Journal(Natural Science Edition), 2011，25(1):16-19.

[18] 庄楚强,何春雄.应用数理统计[M].广州:华南理工大学，2006.

[19] 孙淑生,罗宝花.多元线性回归模型在物流成本预测中的应用[J].商业时代，2014(18)：19-21.

SUN Shusheng, LUO Baohua. Application of Multiple Linear Regression Model in Forecasting Logistics Costs[J]. Commercial Times, 2014,(18):19-21.

[20] 周晓娟，景志英.基于多元线性回归模型的河北省物流需求预测实证分析[J].物流技术，2013，32(5)：270-272.

ZHOU Xiaojuan, JING Zhiying. Empirical Analysis of Logistics Demand Forecasting of Hebei Based on Multi-linear Regression Model[J]. Logistics Technology,2013,32(5):270-272.

[21] 武进静，韩兴勇.基于多元线性回归模型对江苏省物流需求的预测分析[J].上海农业学报，2015,31(4)：62-68.

WU Jinjing, HAN Xingyong. Forecasting and Analysis of Jiangsu Province’s Logistics Demand Based on Multiple Linear Regression Model[J]. Acta Agriculturae Shanghai, 2015,31(4):62-68.

(编辑查黎)

ResearchonCalculationModelforAmountofPrimaryMaterialsof110kVandAboveTransformersBasedonMultipleLinearRegressionAnalysis

LIUPingyuan1,ZHANGLei2,WANGYu3,XIEPeng1,2,LUQifu3,LIAOJiajun2

(1.MaterialDepartmentofSouthernChinaPowerGridCo.,Ltd.,Guangzhou,Guangdong510623,China; 2.SouthChinaUniversityofTechnology,Guangzhou,Guangdong510640,China; 3.ElectricPowerResearchInstituteofGuangdongPowerGridCo.,Ltd.,Guangzhou,Guangdong510080,China)

Inordertomoreaccuratelycalculatecostofeffectivematerialsincludingsiliconsteelsheetsandcopperwiresofthetransformer,themultiplelinearregressionmethodisusedtoconfirmmainperformanceparametersinfluencingcostoforiginalmaterialsaccordingtohistoricaldataprovidedbythosemainstreamtransformersuppliers.Takingno-loadlossandloadlossasinput,amountsofsiliconsteelsheetsandcopperwiresasoutput,acalculationmodelforcostoforiginalmaterialsofthetransformerunderdifferentvoltagelevelsandcapacitiesisestablished.Bycomparingwithmethodofcapacitygrowthlaw,applicabilityofthiscalculationmethodandmodelisfurtherverified,whichcanprovideeffectivebasisformanagementonprocurementcostofthetransformer.

transformer;siliconsteelsheetandcopperwire;multiplelinearregression;no-loadloss;loadloss

2015-12-30

2016-03-18

10.3969/j.issn.1007-290X.2016.07.012

TM41

A

1007-290X(2016)07-0059-08

刘平原(1978)，男，湖北钟祥人。高级工程师，工学博士，从事高压外绝缘、电气设备质量管理方面的研究和应用工作。

张磊(1992)，男，湖南益阳人。在读硕士研究生，从事电气设备全寿命周期及质量管控方面研究。

王宇(1984)，男，河北保定人。工程师，工学硕士，从事电网设备器材检验及物资品控工作。