压气机动叶片振动数学模型建立及动态特性研究
刘志博,尹洪,邓小文,丁常富
(1.广东电网有限责任公司电力科学研究院,广东 广州 510080;2.华北电力大学 能源与动力工程学院,河北 保定 071003)
压气机动叶片振动数学模型建立及动态特性研究
刘志博1,2,尹洪1,邓小文1,丁常富2
(1.广东电网有限责任公司电力科学研究院,广东 广州 510080;2.华北电力大学 能源与动力工程学院,河北 保定 071003)
为探究压气机动叶片受激振力影响下的动态特性,结合某燃机叶片基本参数,对压气机动叶片建立了振动数学模型,通过MATLAB中的Simulink平台进行仿真,获取叶尖在恒速和变速旋转状态下受激振力影响的振动位移曲线。结果表明:恒速条件下,叶片同步振动和异步振动图像差异较大;高频激振下的叶片振动位移幅值远远小于低频激振下的叶片振动位移幅值;变速扫频下能够辨识多个共振区的振动特征。
压气机动叶;数学建模;激振力;振动;仿真
重型燃气轮机(以下简称“燃机”)以天然气为燃料,是高效洁净发电系统的重要动力设备,也是电网调峰的重要手段。作为重型燃机的核心部件,压气机的安全运行至关重要[1]。压气机内部流动复杂,动叶片易受激振力影响发生振动,引发叶片疲劳,出现裂纹、折断等故障[2]。国外采用多只叶尖定时传感器对压气机动叶片振动情况进行监测,保障叶片安全运行[3-5]。本文通过对叶片受力分析,建立压气机动叶片振动数学模型,在叶尖定时监测叶片振动原理的基础上,结合某燃机叶片基本参数,利用MATLAB中的Simulink模块进行仿真,研究了叶片在恒速和变速运行工况下受不同频率激振力影响的振动特性。
1 压气机动叶片振动数学模型建立
1.1压气机动叶片受力分析
实际运行过程中,压气机旋转叶片相对于轮盘为柔性体,忽略叶片与轮盘之间的耦合,即叶片与轮盘之间的耦合阻尼为零。但由于叶片自身材料的固有属性,在振动过程中,叶片自身的反复加载和卸载造成了能量消耗,对叶片振动产生阻尼,即所谓的滞后阻尼。由于离心力主要使叶片产生径向拉伸,在此不做考虑[6]。叶片受力情况如图1所示。
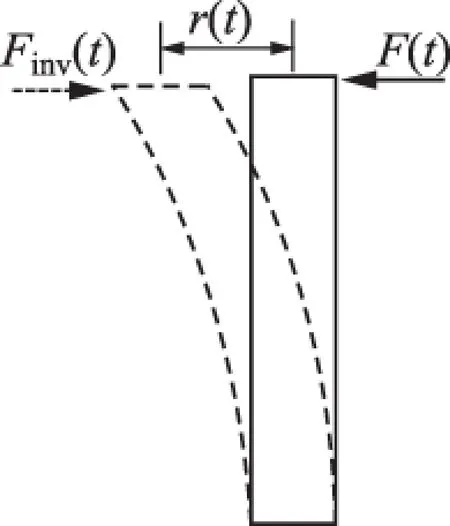
图1 压气机动叶片受力分析
图1中:F(t)为叶片在旋转过程中受到周期变化的激振力,N;r(t)为叶尖发生振动位移,m;Finv(t)为叶片因材料属性及受到流体阻力共同形成反激振力,N。
1.2压气机动叶片振动系统线性化处理
取压气机动叶片为研究对象,由牛顿定律得
(1)
式中:m为叶片质量,kg;a(t)为叶片加速度,m·s-2;Finv(t)与r(t)及速度υ(t)有关,即
(2)
将Finv(t)按Taylor级数展开,取其一次项,则


(3)
其中 f(0,0)为一恒力,在进行振动分析时,作用在叶片上的恒力及其引起的静位移可同时略去不记[6],令
(4)
(5)
则
(6)
带入式(1)并整理,得压气机动叶片振动数学模型

(7)
式中:c为阻尼系数,N·s·m-1;k为抗弯刚度,N·m-1。令
(8)
(9)
式中:ωn为叶片自由振动角频率,Hz;ξ为阻尼率,常数。
根据傅里叶级数,叶片承受的任何形式的动载荷F(t)都可以表示为
(10)
式中:Fi为对F(t)进行傅里叶变换后的各个振动频率相对应的力幅值,N;Ni为各个自然倍频;di为与Fi相等的恒力作用在叶片上所引起的静位移,m;ω为压气机转速角频率,Hz;φi为与Ni对应的初始相位。
仿真过程中,通过改变自然倍频N值得到不同频率激振力影响下的叶尖振动位移。将式(8)、式(9)、式(10)代入式(7)得
(11)
上式的解为

(12)
其中
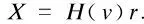
(13)
(14)
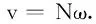
(15)
(16)
式(16)对v求导并令其等于零,得H(v)的极大值解
(17)
以上各式中:v为激振频率;vr为共振频率;H(v)为放大系数。
将vr代入式(16)得H(v)的极大值表达式
(18)
当激振频率等于vr时,H(v)取得极大值H(vr), 系统达到共振。
假设叶片质量为1.578kg,叶片抗弯刚度2.491 9×106N·m-1,由式(8)得叶片自由振动角频率200Hz。令阻尼率为0.25,通过式(9)、式(14)、式(16)、式(17)、式(18)得叶片滞后阻尼系数为991.491N·s·m-1,共振频率为187Hz。
2 压气机动叶片振动仿真模型建立
根据叶尖定时原理,通过叶根同步传感器获得转速同步信号,旋转周期为T,以此作为基准,通过叶尖定时传感器,叶片经过传感器探针时刻,相对转轴基准的到来时间序列为{tj}(j=1,2,…,n),对{tj}进行数学换算即可得到叶尖振动位移值[7]。
将压气机动叶片振动数学模型式(7)改写为
(19)
在MATLAB图形仿真平台Simulink中建立基于叶尖定时原理的叶片振动系统模型。通过转速频率函数f(t)设定叶片转速,F(t)为谐波函数,其数学表达式为

(20)
经时间模块将仿真时间t输入f(t)和F(t)中,叶尖振动位移值经积分模块求解得到。结合叶片振动数学模型,所创建的Simulink模型框图如图2所示。

1/s—积分模块。图2 叶片振动数学模型
叶尖定时传感器具体安放位置,是通过设置Simulink中的Hitcrossing模块和开关模块内部相关参数来模拟的。完成后的叶片振动系统模型框图如图3所示。
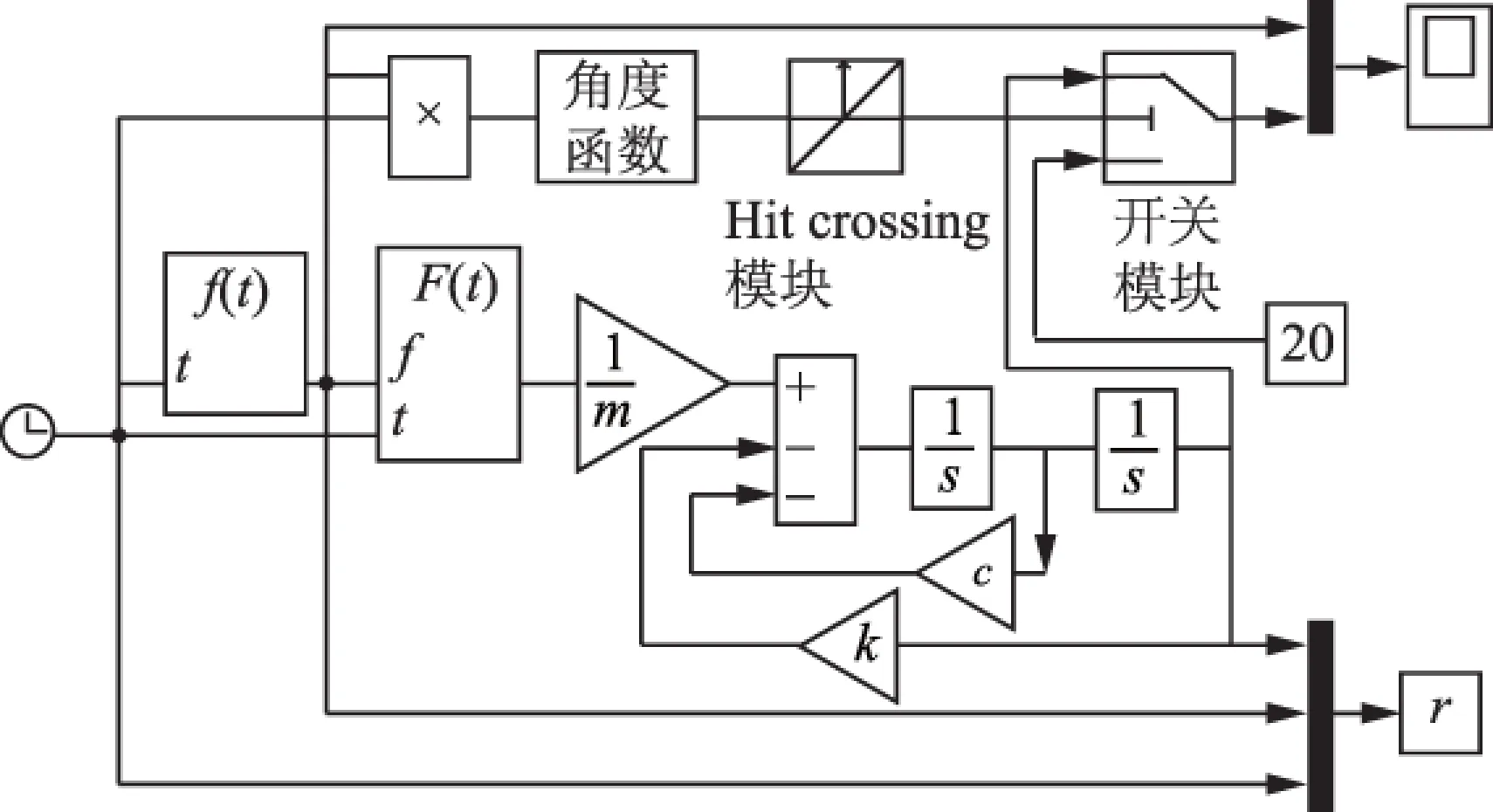
图3 叶尖定时测振模型
3 叶片振动仿真
压气机在启动过程中升速运行,稳定工况下恒速运行。依照压气机运行特点,分别在压气机恒速和升速运行工况下,仿真叶片受到不同频率激振力影响的振动情况,得到叶尖振动及叶尖定时信号特征。仿真过程中通过设定N值的大小,实现对叶片加载不同频率激振力。模拟叶尖定时传感器安放位置为20°,如图4所示。

图4 叶尖定时传感器安放位置示意图
3.1恒速下叶片振动仿真
3.1.1叶片受恒力影响
假设叶片转速为1 200r·min-1,对应转速频率为20Hz,改变激振力为恒力Fc(Fc=kd),仿真时长50s,得到恒力下叶尖在20°处和在周向各个位置处的振动位移曲线如图5所示。

(a) 20° (b)周向 图5 叶片受恒力影响
受Fc影响,叶尖在20°处偏离平衡位置大约0.63mm。周向各个位置叶尖位移值也基本稳定在0.63mm处,没有发生振动。
3.1.2叶片受低频激振同步振动
将N值设为1,激振力力幅大小与第3.1.1节仿真时的恒力值大小相等,设激振力的初相位值为0°,其他设置参数不变,得到低频(20Hz)激振力下的叶尖振动位移曲线如图6所示。
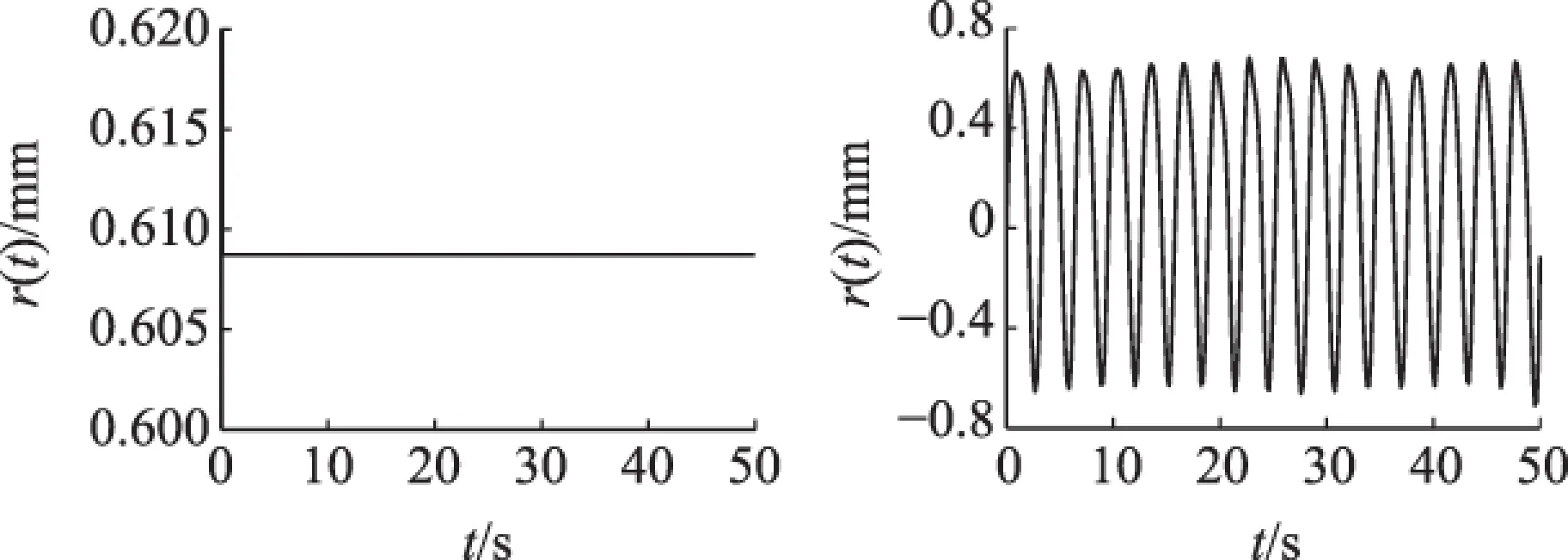
(a) 20° (b) 周向 图6 叶片受低频激振影响
叶片在圆周20°处的振动位移值恒定,约0.605 7mm。叶片在旋转过程中受低频激振影响,振动位移值在-0.62~+0.62mm范围内波动。
3.1.3叶片受高频激振同步振动
N值设为40,其他设置参数不变,得到叶片恒速下受高频(频率为800Hz)谐波激振力影响的振动曲线如图7所示。
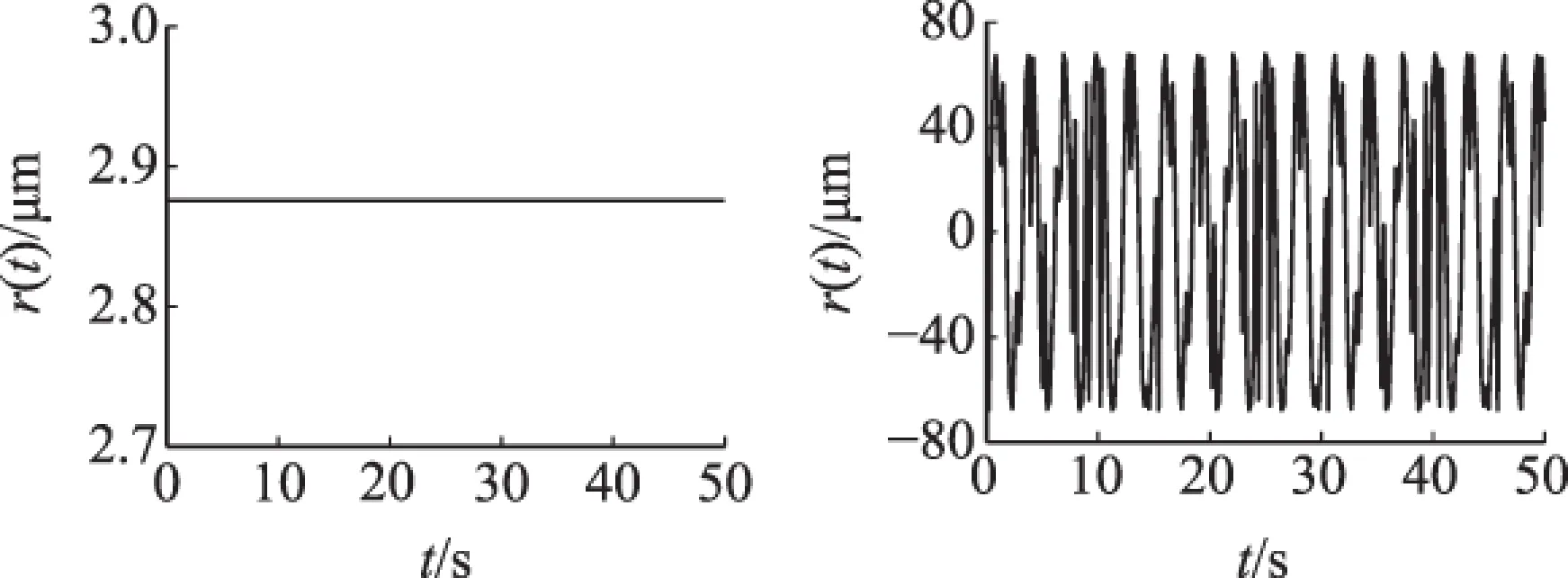
(a) 20° (b) 周向 图7 叶片受高频激振影响
在高频激振下,由于惯性作用,叶片的振动位移很小,在圆周20°处的振动位移值依然恒定,约2.87μm。在周向各个位置处,振动位移值在-70~+70μm范围内波动,是恒速下叶片受低频激振力影响振动位移最大幅值的十分之一左右。
3.1.4叶片异步振动
当激振力频率与叶片转速频率不成整数倍关系时,叶片发生异步振动。令N值为1.5,其他参数设置不变,结果如图8所示。

(a) 20° (b) 周向 图8 叶片异步振动
叶片在圆周20°处的振动位移值与叶片同步振动不同,随着时间的不同为一变值。从周向各个位置处的叶片异步振动图像可见,叶片振动位移值在-0.7~+0.7mm之间波动。
综合以上仿真内容,本文建立的基于叶尖定时原理的振动系统模型,对于燃机稳定运行过程中各个频段的同步振动和异步振动,均可以进行仿真扫描。通过仿真图像可知:叶片受低频激振时,振动幅值较大;高频激振时,由于惯性作用,叶片来不及对激振做出响应,所以只在极其微小的幅值范围内波动;对于异步振动,在同一个监测点测得的叶片振动图像与同步振动图像差别较大。
3.2变速下叶片振动仿真
3.2.1叶片共振
假设叶片转速从1 200r·min-1经50s线性升速到3 000r·min-1,对应的旋转频率变化范围为30Hz到50Hz,将N值设为4。叶尖振动曲线如图9所示。
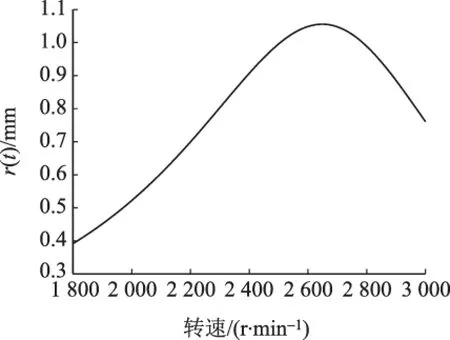
图9 变速下叶片共振(20°)
在转速大约为2 700r·min-1时,叶尖振动位移增大至1.05mm左右。此时叶片对应的振动频率为180Hz,接近叶片的共振频率187Hz,引起叶片共振。
3.2.2叶片变速扫频
上述仿真为单倍频(N=4)激振力,实际在叶片变速扫频过程中将出现多个倍频处的共振区。依然假设叶片转速从1 200r·min-1经50s线性升速到3 000r·min-1,对应转速频率为f1=20Hz至f2=50Hz,叶片共振频率vr=187Hz,扫频经过的倍频由公式
(22)
确定,可得到N值为4、5、6、7、8、9共6个倍频值。扫频过程中叶片振动曲线如图10所示。

图10 叶片变速扫频(20°)
升速过程中叶片变速扫频,在多个位置处振动位移突然增大,表明叶片经过了多个共振区。
4 结束语
本文对压气机动叶片振动进行理论分析,基于叶尖定时原理建立了压气机动叶片振动数学模型。以压气机升速过程和稳定运行工况为场景,仿真压气机动叶片在恒速和变速下受不同频率激振的振动情况。对于燃机稳定运行过程中各个频段的同步振动和异步振动,建立的振动系统模型均可以进行仿真扫描。通过仿真直观地反映出叶尖振动及叶尖定时信号特征:叶片受低频激振时,振动幅值较大;高频激振时,叶片只在微小幅值范围内波动;叶片异步振动图像与同步振动图像差别较大;变速时,可辨识出多个共振区的振动特征。
[1] 林公舒,杨道刚.现代大功率发电用燃气轮机[M].北京:机械工业出版社,2007.
[2] DREWCZYNSKIM, SOLINSKIM,RZADKOWSKIR. A Compressor of Two Load Transferring Methods in an Unsteady One-way Fluid-structure Interaction Analysis[C]//Proceedings of ASME Turbo Expo 2012.Copenhagen:ASME,2012:34-43.
[3] KESTNERB,LIEUWENT,HILLC,et al. Correlation Analysis of Multiple Sensors for Industrial Gas Turbine Compressor Blade Health Monitoring[C]//Proceedings of ASME Turbo Expo 2014:Turbine Technical Conference and Exposition.Dusseldorf:ASME,2014:113-123.
[4] 朱宝田,肖俊锋,祁文玉.某电厂3号燃气轮机压气机叶片故障原因分析[J].热力透平,2007,36(1):67-70.
ZHU Baotian,XIAO Junfeng,QI Wenyu.Analysis on Compressor Blade Failure of No.3 Gas Turbine in aCertain Plant[J].Thermal Turbine,2007,36(1):67-70.
[5] 师汉民.机械振动系统—分析·建模·测试·对策(上册)[M].武汉:华中科技大学出版社,2014.
[6] 欧阳涛.基于叶尖定时的旋转叶片振动检测及参数辨识技术[D].天津:天津大学,2011.
[7] 王正林,王胜开,陈国顺.MATLAB/Simulink与控制系统[M].北京:电子工业出版社,2005.
(编辑霍鹏)
Establishment of Mathematical Model for Compressor Blade Vibration and Research on Vibration Dynamic Characteristic
LIU Zhibo1,2, YIN Hong1, DENG Xiaowen1, DING Changfu2
(1. Electric Power Research Institute of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510080, China; 2. College of Energy and Power Engineering, North China Electric Power University, Baoding, Hebei 071003, China)
In order to study dynamic characteristic of compressor blade under exciting force influence, a mathematical model for compressor blade vibration is established by combining basic parameters of some gas turbine blade. By means of simulation on Simulink platform of MATLAB software, the vibration displacement curve of blade affected by exciting force is obtained under conditions of constant and variable speed rotation. Results indicate that under constant speed condition, differences of images of synchronous vibration and asynchronous vibration are great, the vibration displacement amplitude of blade under high frequency exciting force is far less than that under low frequency exciting force and it is able to identify vibration characteristics of multiple resonance regions under the condition of variable speed sweeping.
compressor blade; mathematical model; exciting force; vibration; simulation
2015-12-28
2016-03-01
中国博士后科学基金资助项目(2015M570696);中国南方电网有限责任公司科技项目(GDKJ00000005)
10.3969/j.issn.1007-290X.2016.07.005
TK474.8+11
A
1007-290X(2016)07-0024-05
刘志博(1990),男,河北张家口人。在读硕士研究生,主要从事振动信号监测研究工作。
尹洪(1987),男,重庆人。在站博士后,工学博士,主要从事燃气轮机等发电设备研究工作。
邓小文(1974),男,湖南祁阳人。教授级高级工程师,工学博士,主要从事燃气轮机等发电设备研究工作。

