凸函数的判定、性质与应用研究

李思凝

(沈阳师范大学数学与系统科学学院，辽宁 沈阳 110000)



凸函数的判定、性质与应用研究

李思凝

(沈阳师范大学数学与系统科学学院，辽宁 沈阳 110000)

摘要：凸函数是一类重要的函数，它的概念最早见于Jensen[1905]著述中。它在纯粹数学和应用数学的众多领域中具有广泛的应用，现已成为数学规划、对策论、数理经济学、变分学和最优控制等学科的理论基础和有力工具。本文着重研究了凸函数，拟凸函数，严格预不变拟凸函数的定义，性质，以及凸函数在经济学中的应用。

关键词：凸函数；拟凸函数；严格预不变拟凸函数；应用

1引言

凸函数是一类重要的函数，在数学的许多领域中都有着广泛的应用，但是它的局限性也很明显。如何推广函数的凸性概念，使得在更广泛的函数范围内，凸函数的许多重要性质仍然得以保留，所以研究广义凸函数的一些定义和性质就显得十分必要了。函数的凸与凹反映在几何上是对应曲线(曲面)的弯曲方向,如图，本文称函数f(x)在[a,b]上凹函数，在[b,c]上是凸函数。

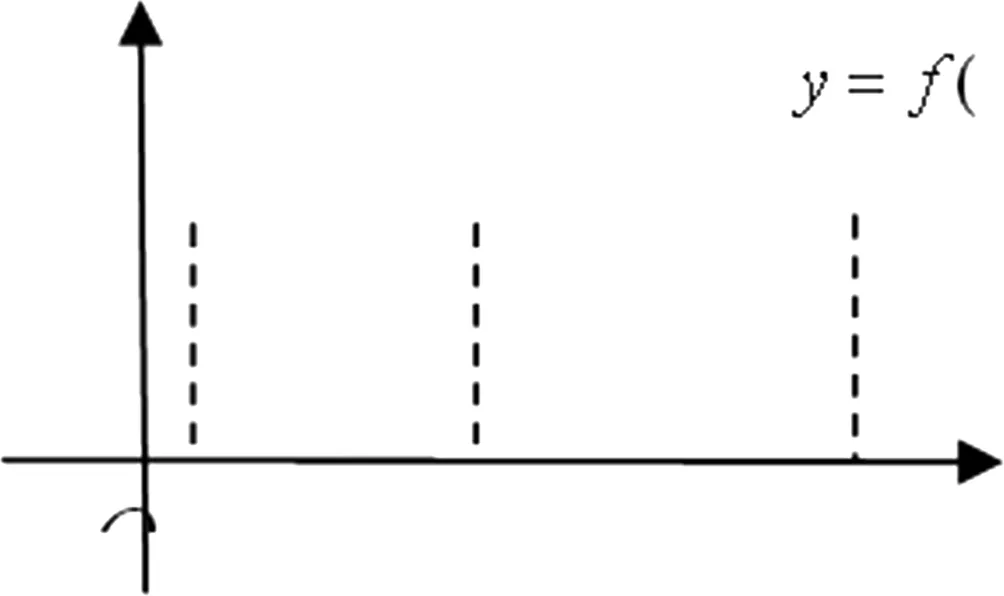
2凸函数的多种定义

定义1设函数f(x)在(a,b)上有定义,若曲线y=f(x)上任意两点间的弧线总位于连接这两点的弦之上,则称f(x)是区间(a,b)上的凸函数。

定义2设函数f(x)在[a,b]上连续,若对于

(1)

则称f(x)是[a,b]上的凸函数。

定义3在区间(a,b)内定义的函数f(x),如果对任意n个点x1,x2,…,xn∈(a,b),有

(2)

则称函数f(x)是(a,b)内的凸函数。

定义4设函数f(x)在[a,b]上连续,若对于∀x1,x2∈[a,b]及

0≤t≤1,f[(1-t)x1+tx2]≥(1-t)f(x1)+tf(x2)

(3)

则称f(x)是[a,b]上的凸函数。

3凸函数在经济学中的应用

无差异曲线用来表示消费者偏好相同的两种商品的所有组合，如下图所示，横轴和纵轴分别表示商品1的数量x和商品2的数量y，曲线L1、L2分别表示两条不同商品组合的无差异曲线。

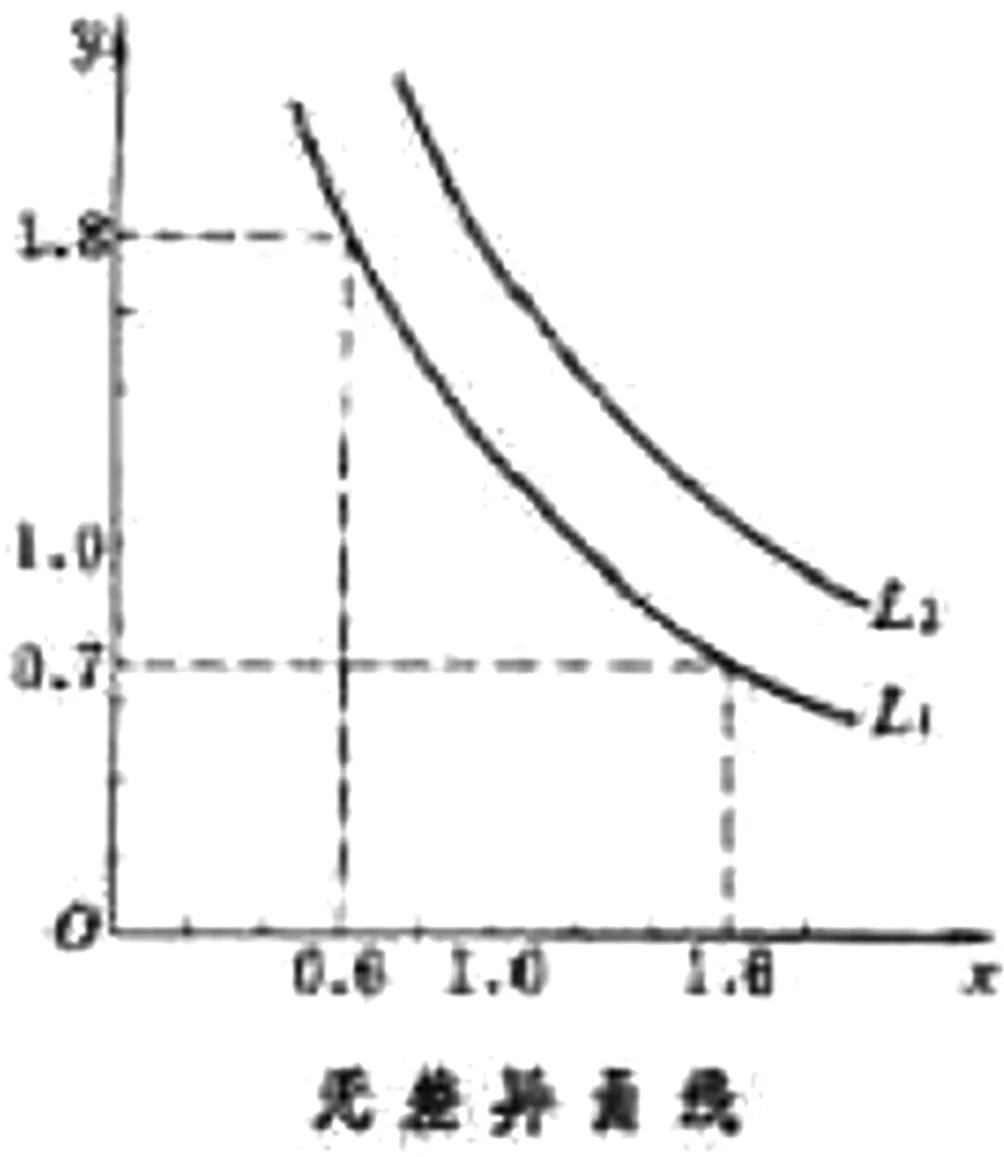
L1曲线是连续的，并在x轴上的具有二阶导数，二阶导数又是大于零的，所以无差异曲线是凸函数。

从上图可以明显地看出，无差异曲线的斜率为负值，而且无差异曲线斜率的绝对值是递减的。商品的边际替代率递减规律决定了无差异曲线具有这样的特征。下面介绍一下边际替代率递减规律。

商品1对商品2的边际替代率的定义公式为:

其中△X1,△X2分别表示商品1和商品2的变化量。

当商品数量的变化趋于无穷小时，则商品的边际替代率公式为

与以上的分析相对应，消费者的风险态度也可以根据消费者的效用函数的特征来判断。一个人是风险厌恶的充要条件是他的效用函数为凹函数。因此，判断一个人是不是风险厌恶者，只需要验证其效用函数是不是凹函数。在判断一个人是不是风险爱好者，只需要验证其效用函数是不是凸函数。消费者对待风险的态度，影响着消费者在不确定情况下的行为决策。如下图所示

该函数是凹函数，且斜率大于零。根据消费者的效用曲线u(x)，消费者在无风险条件下持有一笔确定的货币财富量的效用u(px+(1-p)y)相当于A的高度，而拥有一张具有风险的期望效用pu(x)+(1-p)u(y)相当于图中B的高度。显然A点高于B点。所以，图中的效用函数u(x)满足风险回避者的判断条件。如果从函数的图像来看，自然是曲线向上弯得越厉害，对风险就越厌恶，曲线的弯曲程度可以用函数的二阶导数来刻画。

风险爱好者和风险中立者的效用函数的分析是类似的。在实际经济生活中，大多数的消费者都是风险回避者。

当消费者面临一种风险时，如果对于该消费者而言，风险的期望值的效用大于、小于、等于风险的效用期望时，那么相应地，该消费者的风险态度为风险回避、风险爱好、风险中立。

4总结

经济效益分析：经济活动中，我们可以根据市场调查利用无差异曲线和预算线等的关系来得到商品的需求曲线，厂商会根据曲线获得最大的利润的生产组合，而消费者也可以得到最满意的商品组合。所以利用凸函数的性质描绘无差异曲线在买卖双方的交易活动中起到很大的作用。凸函数分析作为一种强有力的分析工具，在经济工作中应用是很广泛的，掌握了它对指导我们当今的经济工具具有十分重要的意义。

指导教师:关洪岩

参考文献：

[1]刘三阳.凸函数的新发展[J].西安电子科技大学学报,1990,17(1)：45-48.

[2]邱根胜.拟凸函数的几个性质[J].南昌航空工业学院学报,1998,1998(2)：36-39.

中图分类号：G634.6

文献标志码：A

文章编号：1671-1602(2016)14-0296-01