高层建筑下伏溶洞顶板稳定性的可靠度分析

安义军

（贵州地矿基础工程有限公司 贵州贵阳 550081）

高层建筑下伏溶洞顶板稳定性的可靠度分析

安义军

（贵州地矿基础工程有限公司 贵州贵阳 550081）

高层建筑是当前城市建设的重要内容，但是对于岩溶地区，高层建筑的运行安全往往会受到下伏溶洞顶板稳定性的影响。基于此，展开高层建筑下伏溶洞顶板稳定性的可靠度分析十分必要，本文首先对溶洞顶板稳定性评价模型与溶洞顶板功能输出响应模型进行了详细论述，其后探讨了溶洞底板稳定性的可靠度指标确定方法。

高层建筑；下伏；溶洞顶板；稳定性；可靠度

1 引言

在我国岩溶地区，高层建筑建设存在较大的困难，下伏溶洞顶板稳定性的可靠度就是其中的一项。就目前情况来看，我国对该方面的研究还不是很成熟，这在一定程度上阻碍了高层建筑的发展，因此，必须对其进行深入的研究与分析，从而为社会经济的平衡发展奠定基础。

2 溶洞顶板稳定性评价模型

依据相关调查、研究结果发现，通过安全系数，能够最为直接的表现高层建筑下伏溶洞顶板稳定性，因此，对于达到溶洞顶板稳定性要求的预定功能，可通过大于高层建筑工程所需要满足的安全系数限值的溶洞顶板安全系数来表示，具体如下：

式中：K-下伏溶洞顶板安全系数，一般情况下，此系数可通过极限平衡分析方式获得；K标-安全系数限值，此限制的确定主要依据工程规范进行。此外，在不同失稳模式条件下，建筑下伏溶洞顶板安全系数是不相同的，因此，为了确保高层建筑工程的稳定安全性，不论是通过哪一种失稳模式的分析获得的安全系数，都必须大于工程所要求的安全系数限值。在此情况下，式（1）也可以表示为：

式中：Ki-第i种失稳模式分析获得的溶洞顶板安全系数；n-溶洞顶板失稳模式总数。同时，当建筑物下伏溶洞顶板能够达到工程预定功能时，也就是满足式（1）与式（2）的要求时，对于不确定参量，其具有一个允许不确定性变化的幅度，也就是稳定性的可靠度指标，其不仅紧密联系着溶洞顶板的预定功能，还关联着不确定参量种类以及不确定性的实际程度。

一般情况下，不确定参量有设计变量与设计参数两种分类，其中，设计变量主要是指为了确保建筑结构安全性，可以实行的人为调控的参量集合，例如桩径及桩长等；而设计参数则代表不确定性的自然存在，或是因无法避免的系统误差，以及降低的参量集合，导致无法进行人为的调控，例如表现工程地质条件、岩土力学性质方面的参数。对于高层建筑下伏溶洞顶板稳定安全性评价指标，主要是指其安全系数限值、设计变量，以及设计参数方面的函数，具体可表现为：

式中：q-设计变量，一般通过向量形式表示；u-设计参数，也可以通过向量形式表示（q，u，K标）-与设计变量 q、设计参数 u、安全系数限值K标相对应的高层建筑下伏岩溶顶板允许不确定参量的变化幅度值，也就是所谓的稳定性可靠度指标；i—溶洞顶板失稳模式序号，假设其具有 n 种失稳模式，那么，i∈（1，2，3，…，n）。通过（3）可以知道（q，u，K标）值越大，就表示高层建筑下伏溶洞顶板稳定安全性方面允许的不确定参量的变化幅度也会越大，此两者之间存在正比例关系，基于此，可将（q，u，K标）作为稳定性的可靠度指标。

通过比较不确定参量中包含的不确定性变化幅度与稳定性可靠度指标，就能够构建下伏溶洞顶板稳定性评价模型，具体可以下公式表示：

通过式（4）可知，在高层建筑工程中，当不确定参量所涉及的不确定变化幅度处于允许范围内时，溶洞顶板处于一种稳定的状态，相反则处于不稳定的状态。此外，因高层建筑下伏溶洞顶板稳定安全的可靠度指标是式（3）中的设计的设计变量q、设计参数u的函数，所以，对于高层建筑工程的安全稳定性，可采用人为调控设计变量q来实现。

3 溶洞顶板功能输出响应模型

3.1 抗冲切安全系数计算方法

高层建筑抗冲切计算简图如图1所示。通过图1可知：

式中：K1-桩端溶洞顶板抗冲切安全系数；σt-顶板岩体抗拉强度（kPa）；d-桩端直径（m）；h-桩端下溶洞顶板厚度（m），θ-冲切锥台的冲切角（°）；p-桩端荷载（kN）。

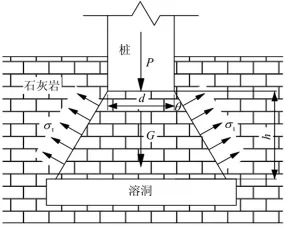
图1 抗冲切计算简图

3.2 抗剪切安全系数计算方法

高层建筑工程抗剪切计算简图如图2所示。通过图2可知：

图2 抗剪切计算简图

式中：K2-桩端溶洞顶板抗剪切安全系数；σs-顶板岩体抗剪强度（kPa）；γ-顶板岩层重度（kN/m3）。

3.3 抗弯安全系数计算方法

高层建筑抗弯计算简图如图3所示。通过图3可知：

式中：K3-桩端溶洞顶板抗弯安全系数；σb-岩体抗弯强度（kPa）；b-建筑计算宽度（m）；M-溶洞顶板所受最大弯矩（kN·m）。

此外，对于高层建筑下伏溶洞顶板稳定安全输出响应模型，可通过将式（5）～（7）代入式（2）的方式获得。但在此过程中，因岩体抗拉、抗剪与抗弯强度很难测量、确定，所以可采用对岩体单轴抗压强度折减的方式获得。由此可知，只要获得了单轴抗压强度，就能够得到抗拉、抗剪、抗弯强度指标值。其中，对于单轴抗压强度，可在依据岩体质量分类指标RMR与Hoek-Brown经验强度准则的条件下进行适当的估算获得，具体为：

图3 抗弯计算简图

式中:σcm-岩体单轴抗压强度；σc-岩石抗压强度；s-Hoek-Brown经验强度准则计算参数。

4 溶洞底板稳定性的可靠度指标确定方法

4.1 确定溶洞顶板稳定不确定参量

对于高层建筑下伏溶洞顶板的不确定参量，其主要包括设计变量与设计参数，对于此参量的确定，可通过式（2）及式（5）～（7）来确定。其中，对于设计变量q，其主要涉及到桩径d，具体可表示为：q=[d]；而对于设计参数u，可表示为：

式中：σc-岩石单轴抗压强度；RMR-岩体质量分类指标；h-桩端下伏溶洞顶板厚度；θ-冲切锥台的冲切角；P-桩端荷载；γ-顶板岩层重度；l-溶洞跨度；H-顶板以上各土层总厚度；γs-顶板以上各土层加权平均重度。

对于稳定性的可靠度指标，通常是以名义值为基础进行计算的，所以，必须先确定合理的、科学的名义值。但是，因下伏溶洞顶板设计变量可以由人为调控，所以，在进行特定的设计稳定性的分析时，可以不考虑设计变量的不确定性，也就是将其作为常数来看待，在此情况下，不确定参量即为设计参数。在高层建筑工程实际施工过程中，对于其设计参数，通常以实测区间数来表示：

式中：uL-设计参数的下限；uU-设计参数的上限。对于涉及的名义值，一般通过设计参数之区间数的中值来表示：

4.3 实测最大不确定性程度α实的确定方法

对于建筑下伏溶洞顶板稳定的不确定参量，主要表现为设计参数，且每一个设计参数的不确定性程度也存在差异。在此情况下，为了确保溶洞顶板稳定性评价的最大包容性，必须将具备最大的不确定性程度的设计参数中的不确定性参数，也就是将α作为下伏溶洞顶板稳定性评价的不确定参量，从而计算出不确定性程度最大变化幅度，即为α实。此时可令c=u，并通过以下公式来确定α实：

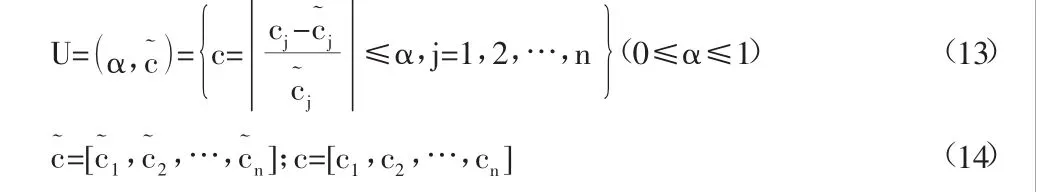
4.4 确定溶洞顶板的稳健可靠度指标

通过式（3）的物理含义可知，溶洞顶板稳健可靠度指标，也就是（q，u，K标），必须具备溶洞顶板稳定安全的预定功能。但对于q，u，K标），必须通过迭代计算来确定，具体如下：

（1）确定不确定性参数α的初始值α0。通过分析式（13）可以知道，α∈[0，1]，所以能够将该区间中值作为不确定性参数的初始值，也就要α0=0.5。

（2）在式（13）的基础上，可通过反算来确定不确定性参数αn对应的设计参数u的区间数，具体可表述为：

（3）确定不同失稳模式下溶洞顶板安全系数。因设计参数是通过区间数来表示的，所以，由式（5）～（7）获得的安全系数依旧是区间数，即为：

式中：KIi，KUi表示在第i种失稳模式条件下，溶洞顶板安全系数区间数的下限值、上限值。但因为设计参数实际上就是区间数，所以，对于溶洞顶板安全系数的计算，实际上就是区间数的运算，在此情况下，可以采用区间数学理论中的区间组合分析方法。

（4）为了满足溶洞顶板稳定的稳健性要求，必须确保式（3）恒定成立，即为：

5 结语

综上所述，高层建筑下伏溶洞顶板稳定性的可靠度往往存在诸多影响因素，这对高层建筑的发展造成了一定的阻碍。为了打破此限制，必须对其进行深入的研究与分析，并采取有效的措施降低或彻底解决这些因素带来的影响，推动高层建筑的持续发展。

[1]龚先兵，赵明华，张永杰.桩端下伏溶洞顶板稳定非概率可靠性分析方法[J].湖南大学学报：自然科学版，2011（01）：13～17.

[2]张俊萌，方从启，朱俊峰.桩基下溶洞顶板稳定性有限元阶段分析[J].工程地质学报，2014（01）：78～85.

[3]李 东.花鱼洞拱座下覆溶洞变形的模拟分析[J].交通科技，2010（05）：34～35.

TU473.1

A

1004-7344（2016）01-0162-02

2015-12-20

安义军（1988-），男，土家族，贵州贵阳人，助理工程师，本科，主要从事各类工程勘察，设计及施工工作。