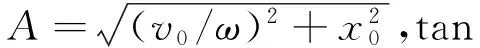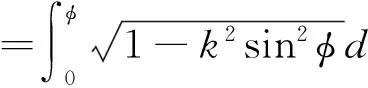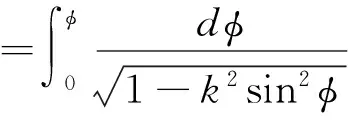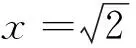非均匀电场中带电粒子的运动特征

黄时中，　郭　蕊，　汪　女曼

(安徽师范大学 物理与电子信息学院，安徽 芜湖　241000)



非均匀电场中带电粒子的运动特征

黄时中，郭蕊，汪女曼

(安徽师范大学 物理与电子信息学院，安徽 芜湖241000)

摘要：本文以均匀带电球体、均匀带电圆盘、均匀带电圆环所产生的非均匀电场为例,分析了带电粒子在这些非均匀电场中的运动特征.分析方法的要点是,依据带电粒子在非均匀电场中的受力情况建立动力学方程,解析地导出带电粒子的运动学方程(多数是以隐函数形式呈现的运动学方程),运用现代数学工具mathematica描绘出带电粒子运动的x-t和v-x图像,以此为基础分析带电粒子在非均匀电场中的运动特征.

关键词：非均匀电场；带电粒子；运动特征

引言

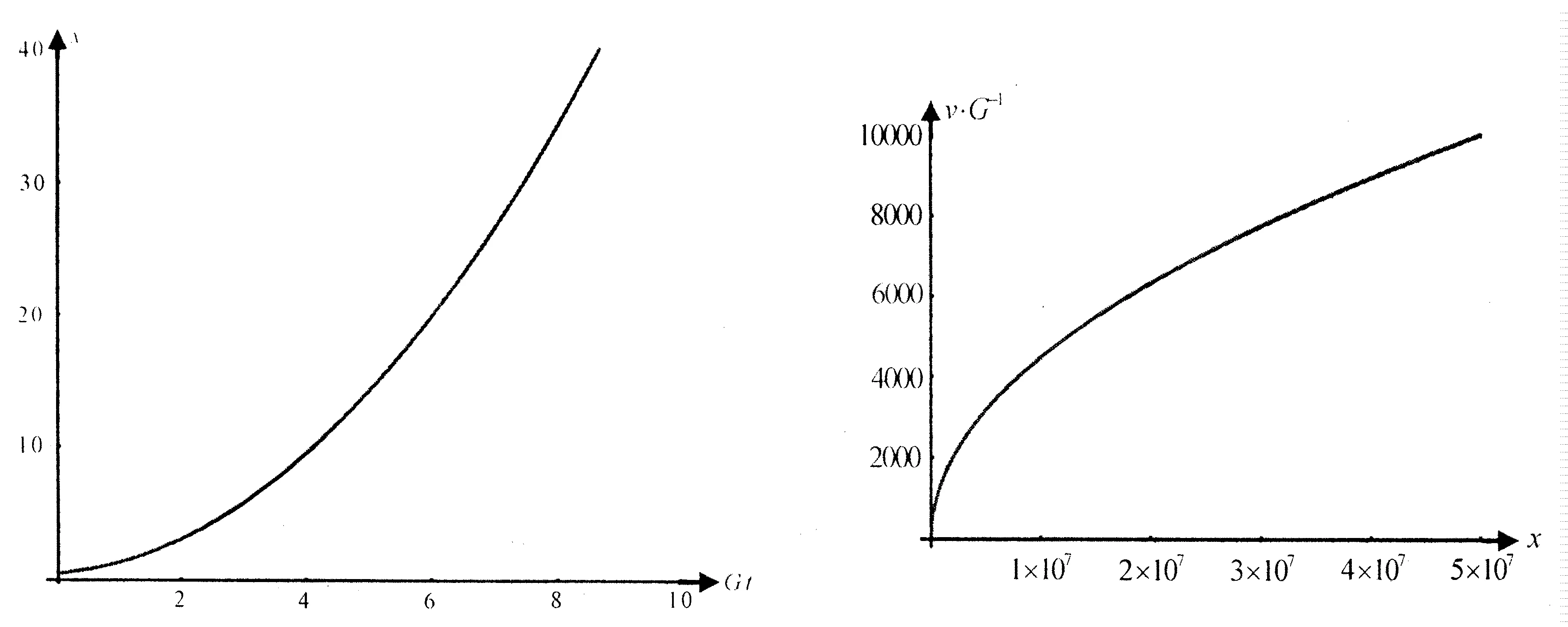
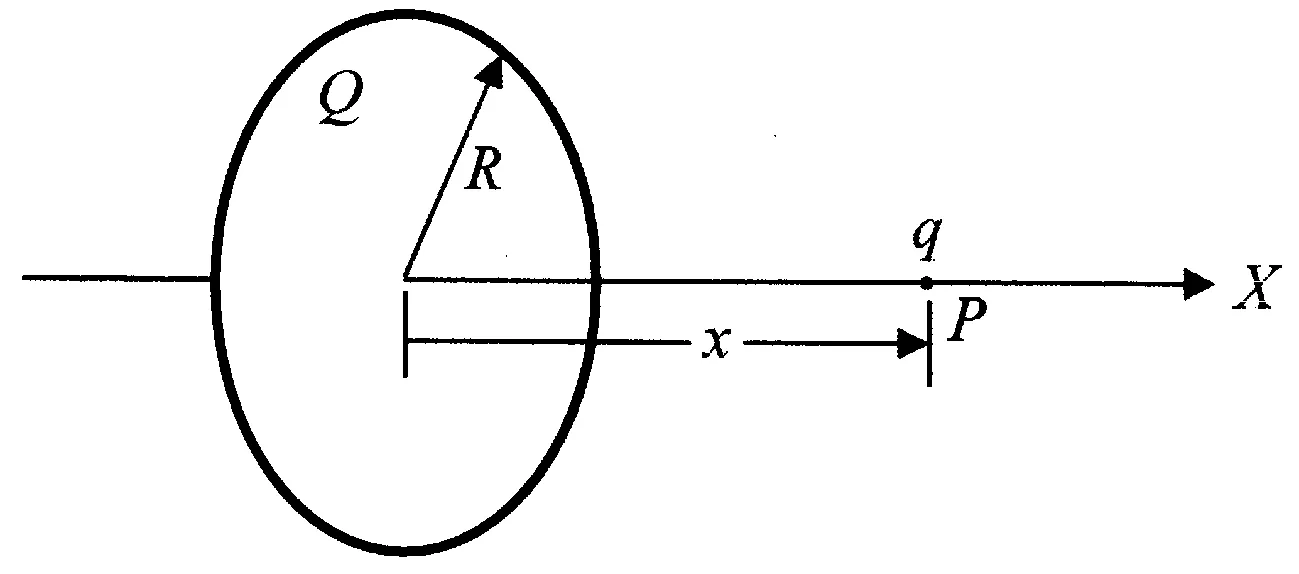
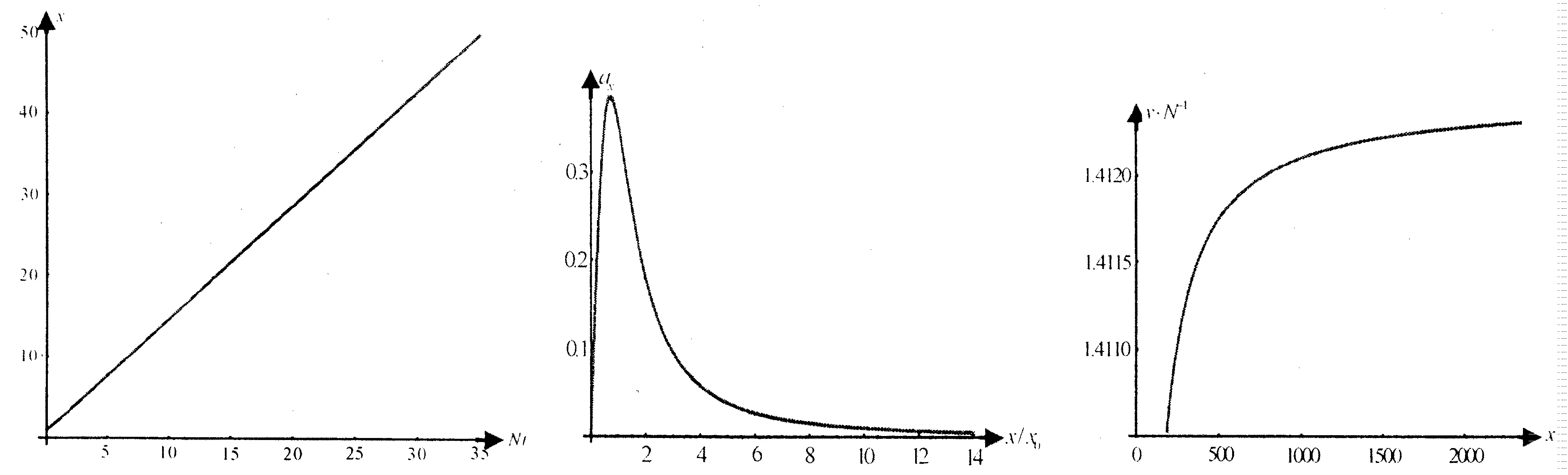
带电粒子在电场中的运动规律是电磁学以及大学物理课程中的重要知识点.众所周知, 实际的电场都是非均匀电场,均匀电场只不过是几种非均匀电场的近似表达形式.然而, 在目前的电磁学以及大学物理教材[1-4]中所介绍的带电粒子在电场中的运动规律基本上都指在均匀电场中的运动规律,至于带电粒子在非均匀电场中的运动规律,除个别特例外,并未作介绍,究其原因在于数学处理上较为复杂.经研究,我们发现,利用近十来年发展起来的现代数学工具Mathematica,可以相当方便地处理这类复杂问题.本文以均匀带电球体、均匀带电圆盘、均匀带电圆环所产生的非均匀电场为例,分析带电粒子在这些非均匀电场中的运动规律.分析方法的要点是,依据带电粒子在非均匀电场中的受力情况建立动力学方程,解析地导出带电粒子的运动学方程(多数是以隐函数形式呈现的运动学方程),运用现代数学工具mathematica描绘出带电粒子运动的x-t和v-x图像,分析带电粒子在非均匀电场中的运动特征. 这种分析方法可以方便地引入到电磁学以及大学物理课程的教学中,从而深化相关知识点的教学改革[5-6],提升教学质量.

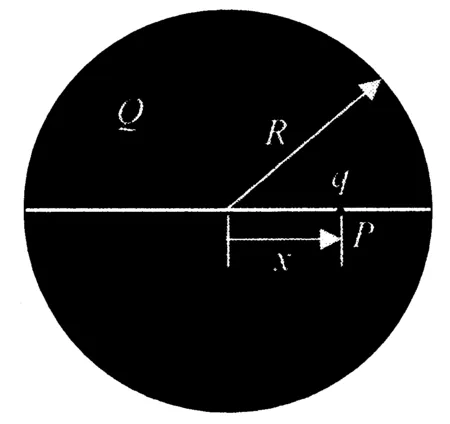
图1　带电粒子在均匀带电球体内部沿轴线的运动

1带电粒子在非均匀电场中的运动特征

设带电粒子的质量为m,初始率为v0,初始坐标为x0,我们来讨论该粒子在非均匀电场中沿X轴作直线运动的几种情形.

1.1带电粒子在均匀带电球体内部沿轴线的运动

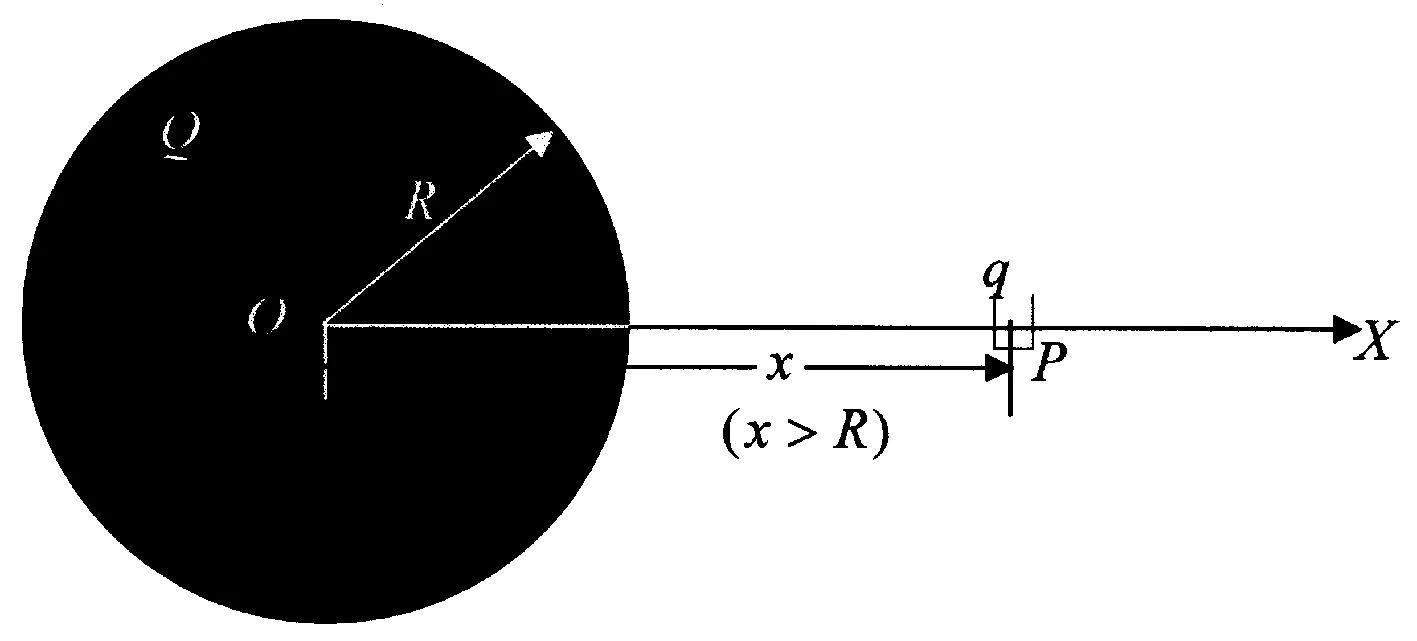
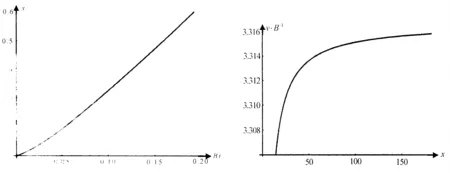
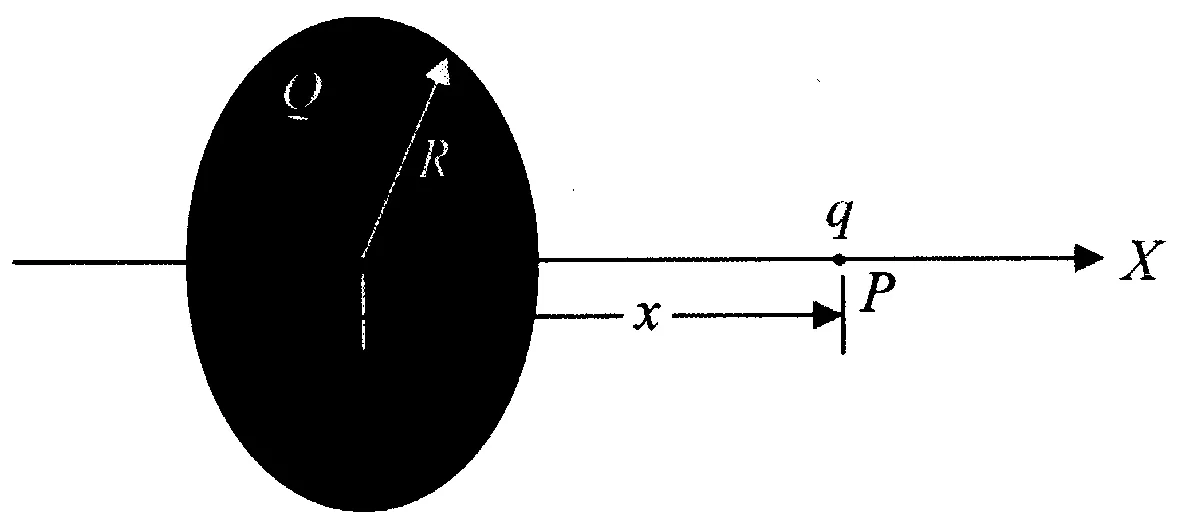
如图1所示, 在半径为总电荷量为Q(Q>0)的均匀带电球体轴线(X轴)上有一个非常细的隧道,一带电粒子(电荷量为-q<0)位于该隧道上, 我们来讨论该带电粒子在带电球体内的运动规律(限定|x|

在与球心相距为x的P点,电场强度的方向沿X轴正向,大小为[1]

(1)

带电粒子所受的作用力是

Fx=-qEx=-kx

(2)

其中

(3)

这种作用力与无阻尼简谐振子所受的作用力的数学形式相同,因而带电粒子在均匀带电球体内部沿轴线的运动是简谐振动[7].

设带电粒子的初速度与X轴平行,且初始坐标和速度分别是x0和v0,则带电粒子的运动学方程的数学形式是

x=Acos(ωt+φ)

(4)

其中

(5)

运动学方程(4)是显函数,其规律是熟知的,无须做进一步分析.

图2　带电粒子在均匀带电球体外部沿轴线的运动

1.2带电粒子在均匀带电球体外部沿轴线的运动

在与球心相距为x的P点,电场强度的方向沿X轴正向,大小为

(6)

带电粒子所受的作用力和加速度分别是

(7)

设带电粒子的初速度与X轴平行,我们来分析带电粒子的速度.根据牛顿第二定律的x分量式，我们有

两边取积分

可得

(8)

其中

(9)

C是由初始条件(初始坐标x0和速度v0)所确定的常量.

方程(8)给出了粒子的运动速度与坐标之间的关系,下面进一步分析带电粒子的运动方程.利用vx=dx/dt,可以将方程(8)改写为

两边再取积分

并利用Mathematica命令完成上式左边的积分，得到

(10)

此即用隐函数f(x,t)=0的形式表示的粒子的运动学方程.利用Mathematica中的绘图命令,可以简便地绘出粒子运动的x-t图像,从而形象地显示出粒子的运动特征. 为了简化绘图操作, 我们参照(9)式取

(11)

利用Mathematica命令绘出的x-t图像如图3.a所示,图中纵坐标的单位是x0,横坐标的单位是Bs.

a. x-t图像　　　　　　　　　　　　　　　　　　　　　b. v-x图像图3　带电粒子在均匀带电球体外部沿轴线运动的图像

图4　带电粒子在均匀带电圆盘轴线上的运动

图3.a所表明的带电粒子在均匀带电球体外部的电场中沿轴线的运动特征是:经历短时间的加速后,带电粒子作匀速直线运动.如何理解这一运动特征呢?其实,由方程(7)可知,随着粒子的位移的增大,粒子的加速度迅速减小,而由方程(8)可知,随着粒子的位移的增大,粒子的速度迅速趋近于常量.利用Mathematica命令绘出粒子运动的v-x图像(图3.b,图中横坐标的单位是x0,纵坐标的单位是v0·B-1),可以直观地看出粒子运动速度的这一特征.

1.3带电粒子在均匀带电圆盘轴线上的运动

如图4所示,半径为R总电荷量为Q(假设Q>0)的均匀带电圆盘的盘心在X轴的原点,将另一带电为q(q>0)的粒子置于X轴上,我们来讨论该带电粒子在X轴上的运动特征.

均匀带电圆盘轴线(X轴)上与盘心相距为x的P点的电场强度为

(12)

带电粒子所受的作用力和加速度分别是

(13)

和

(14)

设带电粒子的初速度与X轴平行,我们来分析带电粒子的速度.将(13)式代入牛顿第二定律的x分量式

得到

两边取积分

可得

由此给出

(15)

其中

(16)

K是由初始条件(初始坐标x0和速度v0)所确定的常量.

下面进一步分析带电粒子的运动方程.利用vx=dx/dt,可以将方程(15)改写为

两边再取积分

并利用Mathematica命令完成上式左边的积分，得到

(17)

其中

(18)

是反双曲函数.

方程(17)即用隐函数f(x,t)=0的形式表示的粒子的运动学方程.利用Mathematica中的绘图命令,可以简便地绘出粒子运动的x-t图像,从而形象地显示出粒子的运动特征.为了简化绘图操作,我们参照(16)式取

(19)

利用Mathematica命令绘出的x-t图像如图5.a所示,图中纵坐标的单位是x0,横坐标的单位是Gs.而依据方程(15)用Mathematica命令绘出的v-x图像如图5.b所示(图5.b中横坐标的单位是x0,纵坐标的单位是v0·G-1).

a. x-t图像　　　　　　　　　　　　　　　　　　　　　b. v-x图像图5　带电粒子在均匀带电圆盘轴线上运动的图像

图6　带电粒子在均匀带电细圆环轴线上的运动

图5所表示的带电粒子在均匀带电圆盘的电场中沿圆盘轴线的运动特征是:带电粒子一直作加速直线运动,且在靠近带电圆盘的区域粒子的速度增大较快,在远离带电圆盘的区域粒子的速度增大较慢.这一运动特征与均匀带电圆盘轴线上电场的非均匀性一致.其实,由方程(12)可知,在靠近带电圆盘的区域,其电场强度最强,近似为Ex≈Q/(2πε0R2),因而在靠近带电圆盘的区域,带电粒子的加速度最大;随着与带电圆盘中心的距离的增大,电场强度迅速减小,因而粒子的加速度迅速减小.由图5.b可以比较直观地看出粒子运动速度的特征.

1.4带电粒子在均匀带电细圆环轴线上的运动

如图6所示,半径为R总电荷量为Q(Q>0)的均匀带电细圆环的中心在X轴的原点,将另一带电为q(q>0)的粒子置于X轴上,我们来讨论该带电粒子在X轴上的运动特征.

均匀带电细圆环轴线上与环的中心相距为x的P点的电场强度为

(20)

带电粒子所受的作用力和加速度分别是

(21)

和

(22)

设带电粒子的初速度与X轴平行,我们来分析带电粒子的速度.将(21)式代入牛顿第二定律的x分量式

得到

两边积分

可以得到

(23)

其中

(24)

下面进一步分析带电粒子的运动方程.利用vx=dx/dt,可以将方程(23)改写为

利用Mathematica命令完成上式左边的积分，得到

(25)

其中

(26)

(27)

(28)

是三类椭球积分,且

(29)

方程(25)即用隐函数f(x,t)=0的形式表示的粒子的运动学方程.尽管这一方程的数学形式非常复杂,但是利用Mathematica中的绘图命令依然可以简便地绘出粒子运动的x-t图像,从而形象地显示出粒子的运动特征.为了简化绘图操作,我们参照(24)式取

(30)

利用Mathematica命令绘出的x-t图像如图7.a所示,图中纵坐标的单位是x0,横坐标的单位是Ns.

a. x-t图像　　　　　　　　　　　　　b. ax-x图像　　　　　　　　　　　　　c. v-x图像图7　带电粒子在均匀带电圆环轴线上运动的图像

另一方面,由方程(23)可知,随着粒子的位移的增大,粒子的速度迅速趋近于常量.利用Mathematica命令绘出粒子运动的v-x图像(图7.c,图中的横坐标的单位是x0,纵坐标的单位是v0·N-1),可以直观地看出粒子运动速度的这一特征.

2结论

综上所述,在不同的非均匀电场中,带电粒子的运动具有不同的特征.运用现代数学工具Mathematica,可以解析地导出在一些常见的非均匀电场(诸如均匀带电球体、均匀带电圆盘、均匀带电圆环所产生的非均匀电场)中带电粒子的运动学方程(多数是以隐函数形式呈现的运动学方程)、描绘出带电粒子运动的x-t和v-x以及a-x图像、分析出带电粒子的运动特征. 这种分析方法可以拓展到对其他非均匀电场中带电粒子的运动特征的分析、可以方便地引入到电磁学以及大学物理课程的教学中,从而深化相关知识点的教学改革,提升教学质量.

参考文献：

[1]黄时中,倪志祥.大学物理(下册)[M].北京：高等教育出版社,2014:140-143.

[2]程守洙,江之永.普通物理学(下册)[M].北京:高等教育出版社，2006:353-362.

[3]梁灿彬.电磁学[M].北京：高等教育出版社,2004:193-199.

[4]贾起民,郑永令,陈暨耀.电磁学(第三版)[M].北京:高等教育出版社,2010:144-150.

[5]黄时中,张丹丹.电场强度与电势梯度关系的简单推导方法[J].安徽师范大学学报:自然科学版,2013,36(2):123-124.

[6]黄时中,张玲,郭蕊.轴截面为正方形的载流长直螺线管内的磁场[J].安徽师范大学学报:自然科学版,2014,37(6):540-542.

[7]黄时中,倪志祥.大学物理(上册)[M].北京：高等教育出版社,2014:98-100.

DOI：10.14182/J.cnki.1001-2443.2016.04.007

收稿日期：2015-11-20

基金项目：安徽省自然科学基金项目(11040606M15),国家自然科学基金专项基金项目(11047019).

作者简介：黄时中(1958-),男,安徽宿松人,教授，博士，主要从事大学物理和理论物理方面的教学和研究工作.

中图分类号：O572.2

文献标志码：A

文章编号：1001-2443(2016)04-0342-07

The Characteristics of a Charged Particle Moving in Non-Uniform Electric Fields

HUANG Shi-zhong,GUO Rui,WANG Man

(College of Physics and Electrical Information, Anhui Normal University, Wuhu 241000, China)

Abstract:The characteristics of a charged particle moving in non-uniform electric fields such as the electric fields generalized by a charged sphere, a charged disc and a charged ring are analyzed. The basic method is as follows: Based on the electric force acted on the charged particle under the non-uniform electric field, the dynamical equation of the charged particle is established, the moving equation of the charged particle is then derived analytically, the x-t and v-x images are drawn by verdure of the modern mathematics tool, mathematica, and finally, the moving characteristics of the charged particle is discussed.

Key words:non-uniform electric field; charged particle; moving characteristic

引用格式：黄时中，郭蕊，汪嫚.非均匀电场中带电粒子的运动特征[J].安徽师范大学学报：自然科学版，2016，39(4)：342-348.