吉林省旅游产品价格满意度调查

□文/张馨文张卜元

（1.吉林财经大学统计学院；2.吉林财经大学国际经济贸易学院 吉林·长春）



吉林省旅游产品价格满意度调查

□文/张馨文1张卜元2

（1.吉林财经大学统计学院；2.吉林财经大学国际经济贸易学院 吉林·长春）

［提要］ 随着高科技的发展，旅游产品种类不断增多，受到许多旅游人士的青睐，不同年龄段人群对旅游景区中旅游产品价格的满意度也不尽相同。对此，本文根据调查数据，运用非参数统计中的Ri di t检验及对数线性模型，对吉林省不同年龄段人群的旅游产品价格满意度进行研究，并提出相应建议。

关键词：旅游产品价格；Ri di t检验；对数线性模型

原标题：不同年龄段人群对旅游产品价格满意度的调查分析——基于吉林省调查数据

收录日期：2016年6月8日

一、数据来源及方法选取

（一）数据来源。本文数据是通过问卷调查方式获得，共收集有效问卷700分。利用spss软件将数据按照年龄段进行分组，其中参与调查并且年龄在20岁以下的共有200人，20～35岁的共有132人，年龄在30～50岁之间的共有50人，年龄在50～65岁之间的共有154人，65岁及以上的共有164人。另外，参与调查的人群中，对旅游产品价格满意度表示非常不满意的共有219人，表示不满意的共有130人，选择一般的有176人，选择满意的共129人，而对旅游产品价格满意度表示非常满意的共有46人。

（二）方法选取。本文首先利用Ridit检验法对吉林省不同年龄段人群对旅游产品价格满意度进行测量，从而判断不同年龄段人群对旅游产品价格满意度是否具有差异。接着本文采用对数线性模型对该问题进行更深入的了解。由于对交互列联表而言，最好的分析方法莫过于对数线性模型，因为该模型不需要区分因变量及自变量，并且可以把列联分析及线性模型统一起来，同时也可以更好地反映变量间的关系。

二、不同年龄段人群对旅游产品价格满意度实证分析

（一）Ri di t得分分析

表1 不同年龄段满意度结果的Ri di t得分

1、计算过程。首先根据原始数据，计算个顺序类别响应总数的一半，得到行（1）；其次将行（1）右移一格，第一格为0，其余为累积前一级（j-1）的累积频率，得到行（2），再次将行（1）与行（2）对应位置相加，即得到行（3）；再次计算各顺序类别的Ridit得分，即将行（3）值除以总数，然后将Rj的值按照Oij占O.j的权重重新配置第i，j位置的Ridit得分，最后计算第i处理类的Ridit得分。

2、计算结果分析。根据上述计算过程及计算公式，可以将所收集数据的整体情况进行Ridit打分，最终打分结果如表1所示。根据公式可以得到，因此平均Ridit得分为0.636，置信区间为（0.6412，0.6578）。（表1）

同时，可以根据上述公式计算不同年龄段人群对旅游产品价格满意度的打分情况，最终结果表示，年龄在20岁及以下的人群中，其Ridit得分为0.545，置信区间为（0.5216，0.5686），年龄在20～35岁之间的人群中，其Ridit得分为0.573，置信区间为（0.4887，0.6568），年龄在35～50岁之间的人群中，其Ridit得分为0.535，置信区间为（0.4536，0.6169），年龄在50～65岁之间的人，其Ridit得分为0.746，置信区间为（0.6996，0.7927），年龄在65岁及以上的人中，其Ridit得分为0.724，置信区间为（0.6792，0.7694）。（表2）

从得分结果看，由于R1、R2、R3的值都小于平均值0.6359，因此认为年龄在50岁以下的人群中，其满意度情况较总数700例的满意度情况好；年龄在20～25岁的置信区间与总体置信区间出现相交的情况，说明该组人群与总数700例的满意度情况差别较小，而其他年龄段的人，其置信区间与整体置信区间没有出现相交的情况，因此与整体具有较为显著的差异。

（二）对数线性模型

1、行变量与列变量独立性检验。由于对数线性模型分为饱和模型及不饱和模型，因此需要对行变量及列变量进行独立性检验，若拒绝原假设，则认为二者不独立，需要建立饱和模型；若接受原假设，则认为二者具有独立性，需要建立不饱和模型，本文利用R软件对相关数据进行检验，检验程序及结果如下：

通过上述结果可知，自由度为（5-1）×（5-1）=16，卡方值为73.423，卡方检验结果的p值为2.49×10-9，由于p值小于0.05，因此拒绝原假设，认为行变量与列变量之间不独立，即年龄与旅游产品价格满意度之间有一定关联。最终可以确定该对数线性模型为饱和的对数线性模型。

2、旅游产品价格满意度联合分布频率。首先，计算所收集数据的频率，由计算结果可知，50岁以下的人群中，其对旅游产品价格满意度为非常不满意的占比最高，非常满意的占比最低，年龄在50～65岁之间的人群中，对旅游产品价格满意度表示满意的人数占比最高，年龄在65岁以上的人群中，对旅游产品价格满意度表示一般的人数占比最高，由此可见，年龄偏大的人，其对旅游产品价格满意度较好，而年纪较小的人，其旅游产品价格满意度往往不高。另外，从总体来看，对旅游产品价格满意度表示非常不满意的人占比最高达到31.3%，表示非常满意的人占比最低，仅有6.6%。通过上述分析，我们可以看到，目前吉林省地区人们对旅游产品价格不尽满意。

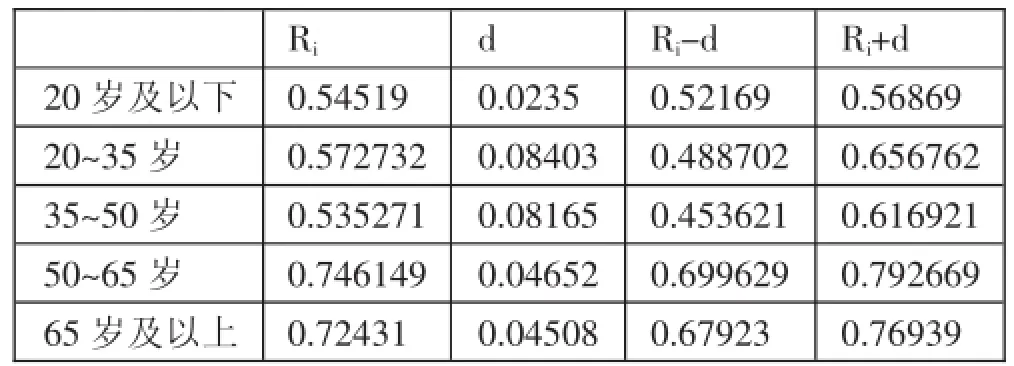
表2 不同年龄段满意度的Ri值

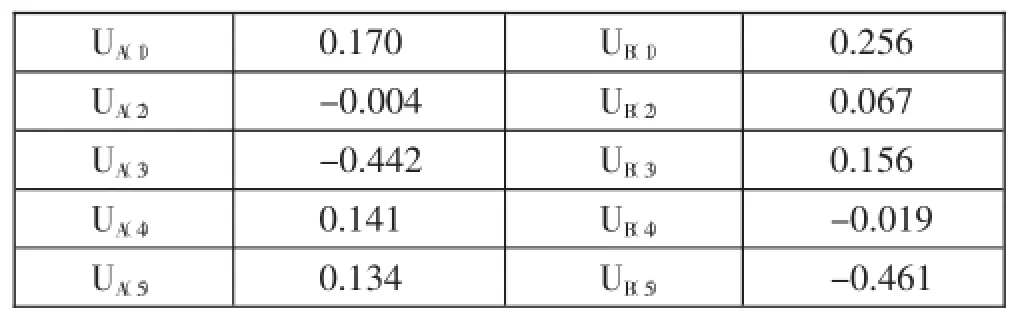
表3 行效应及列效应

表4 交互作用

3、旅游产品价格满意度联合分布概率。通过旅游产品价格满意度的联合分布频率表，可以利用公式pij/pi.p.j，求出旅游产品价格满意度联合分布概率，结果显示了旅游产品价格满意度与年龄的交互作用与1比较的大小，其中最小值为0.046，最大值为1.586，均显示了偏离独立性的特点，并且最小值在年龄层20～35岁之间，最大值在年龄在50～65岁之间。因此，可以认为，年龄在20～35岁之间的人，对旅游产品价格满意度表示非常满意的人最少，可见该年龄段的人对旅游产品价格不够满意，年龄在50～65岁之间的人，对旅游产品价格表示满意的人最多，也就是说，该年龄段的人对旅游产品很满意。

4、旅游产品价格满意度格子分布概率的对数。为了将模型由乘法模型转换为加法模型，则需要将原始数据取对数，并分别求出取对数后的行合计值、列合计值，并用行合计值及列合计值除以对应的行列数，最终得到行平均值及列平均值，而将全部格子分布概率的对数相加后除以总的格子数，就会得到模型中的常数效应。经过计算后，模型的常数效应u=1.325。

5、旅游产品价格满意度的行效应及列效应。根据公式UA（i）=1/s∑lnpij-u；UB（i）=1/r∑lnpij-u，可以得到相关数据的列效应及行效应，最终结果如表3所示。其中，行效应之和等于0，列效应之和也等于0。（表3）

6、旅游产品价格满意度行变量及列变量交互效应。根据模型公式lnpij-u-uA（1）-uB（1）就可以计算出交互作用参数uAB（1j），该值可以用来表示偏离独立性的大小，利用之前求得的相关数据，经计算可以得到结果。其中A（i）和B（j）相交的位置处表示uAB（1j）。由表4可以看出，对旅游产品价格表示非常不满意的人群中，与零差距最大的是uAB（11），对旅游产品价格表示不满意的人群中，与零差距最大的是uAB（52），对旅游产品价格表示一般的人群中，与零差距最大的是uAB（52），对旅游产品价格表示满意的人群中，与零差距最大的是uAB（42），对旅游产品价格表示非常满意的人群中，与零差距最大的是uAB（11），即年龄在20岁以下的人群中，对旅游产品价格表示非常不满意及非常满意的数据偏离独立性较大，年龄在65岁以上的人群中，对旅游产品价格表示不满意及一般的数据偏离独立性较大，年龄在50～65岁之间的人群中，对旅游产品价格表示满意的数据偏离独立性较大。（表4）

三、结论及建议

通过上述分析可以看到，吉林省地区各年龄段人群对旅游产品价格表示非常不满意的人数最多，表示非常满意的人数最少。此外，吉林省地区，被调查者年龄与旅游产品价格满意度之间不具有独立性，即年龄与旅游产品价格满意度之间有一定关联。通过分析可知，年长者对旅游产品价格满意度相对于年轻人要好，对旅游产品价格最不满意的人群中，年龄主要集中在35～50岁之间。其中，20岁以下的人群多为学生，其对旅游产品价格不太满意主要是因为自身收入不多，对学生而言，应该学会适当消费，量入为出；年龄在20～50岁之间的人群更应该做到既享受旅游过程又能做到合理消费。而年龄在50岁以上的人群中，对旅游产品价格满意度的比重偏高，这主要是因为该类人群多数已经处于退休阶段，生活节奏变慢，经济压力减小，追求高品质旅游消费，并能承担起这份开支，所以能接受旅游产品的价格浮动，但是这类人群的主要收入为转移性收入和理财收入，故也应当在旅游中学会合理平衡消费。

主要参考文献：

［1］王星.非参数统计［M］.中国人民大学出版社.

中图分类号：F59

文献标识码：A