树冠微观尺度流动阻力特性分析

王冰清，付海明

(东华大学 a. 环境科学与工程学院；b. 国家环境保护纺织工业污染防治工程技术中心，上海 201620)



树冠微观尺度流动阻力特性分析

王冰清a, b，付海明a， b

(东华大学 a. 环境科学与工程学院；b. 国家环境保护纺织工业污染防治工程技术中心，上海 201620)

摘要：采用可视化Basic程序设计语言(VBA)建立虚拟的三维树冠模型，并使用计算流体动力学(CFD)模拟的方式，研究了不同孔隙率和风速下，树冠内部的流场特征和流动阻力. 用光学孔隙率及体积孔隙率来表征树冠复杂的形态结构，并讨论了树冠形态结构参数对树冠流动阻力的影响规律. 结果表明，树冠的阻力系数与光学孔隙率满足近似二次多项式关系，通过对数值模拟计算结果回归分析，给出树冠流动阻力系数与光学孔隙率的关系式，在真实条件下树冠阻力系数的试验数据对比的基础上，提供了一个对真实树冠阻力系数进行预测的依据.

关键词：树冠； 阻力系数； 孔隙率； 微观模型

森林是陆地生态系统中重要的因素，在全球的生态平衡中有着重要的作用.树木具有保护水土、防风固沙、涵养水源、调节气候、减少污染物等功能.自然或人为作用会使土壤流失、土壤结构发生改变.防风林的栽种有助于防止土壤流失、减少风蚀，最终使风速降低.充分树冠密度下树木的种植或自然植被覆盖的维护会降低风蚀的可能性.文献[1]研究表明，在农田中防风林使农作物免受风灾，其创造了一个提高农作物生产率的有利微环境.若使防风林的效益最大化，还需要深入理解风和障碍物相互之间的物理作用.

尽管研究者们在防风林和大范围孤立障碍物背风处的气流测量和特征描述上做了很多努力，但是对单个植被内气流绕流相互作用而产生的阻力系数方面关注较少.正是由于此相互作用，在微观层面上，观察背风处流域是可靠的.通常，研究分为两方面：(1)剪切应力分区，这里植被的作用是保护固定表面的土壤[2-10]；(2)防风林对流场和微气候的影响[11-14].在第二方面中，大部分的工作用来描绘二维篱笆流场，因此这提高了对文献[15]中二维人造篱笆的遮挡效应和空气动力学的理解.文献[16]总结了二维篱笆孔隙率与阻力系数的曲线关系的研究.实心篱笆的阻力系数最高，并随着孔隙率增大而持续减小.

已有的研究[1]对于防风林、孤立树木和灌木等三维多孔介质绕流流动的理解很不完整.由于模型中代替数据的使用造成了这部分结论的缺失，文献[7-8]的研究使用了文献[16]中的实心粗糙度物体阻力系数来代表自然多孔的植物.风速减小、压力扰动的原因正是由于渗透率和阻力，但是三维多孔介质的原因是未知的[15].防风林阻力系数的测试大部分是通过障碍物周围的风场动量损失的计算完成的[12-13，15，17].但也有其他尝试，例如，通过缩放植被比例的风洞试验进行阻力系数测量[1].风洞研究也测量了阔叶[18]、云杉树枝[19]及整树[20]的阻力.

因此，研究树冠层结构参数与树冠阻力系数的关系对于预测防沙护林的作用是至关重要的.本文采用可视化Basic程序设计语言 (VBA)建立虚拟的树冠模型，并采用计算流体动力学(CFD)模拟计算得出虚拟树冠阻力，通过对数值模拟计算结果回归分析，给出树冠流动阻力系数与光学孔隙率的关系式，并进行真实条件下树冠阻力系数的试验测试，将试验结果与模拟结果进行比较，为真实树冠的阻力系数预测提供计算依据.

1物理模型

本文真实树木与模拟模型中虚拟树木的比例为10∶1.计算流域高为3h，长为5h，宽为防护林平均行距3.5 m，其中h为树冠的平均高度.因此，如图1所示为本文模拟的计算域，设树冠高度为0.25 m，流域高为0.75 m(3h)，长为1.25 m(5h)，宽为0.35 m. 流域高度为3倍树冠高度，故可忽略流域高度对流场求解结果的影响.为保证入口边界和出口边界处流动的充分发展，设定树冠到流体入口边界距离为0.625 m，即2.5倍树冠高，树冠到流体出口边界距离为0.625 m，亦为2.5倍树冠高.流域被划分为8 385 633个非均匀四面体网格，并对树冠内部作局部网格加密处理.边界条件：流域的底部设置为粗糙壁面，粗糙度取0.005 m,并假设壁面无明显的障碍物和植被.除了入口和出口以外，计算流域的其他壁面包括树枝和树叶的表面均设为无滑移壁面边界条件.入口设置为速度入口边界条件，出口设置为相对压力为0的压力出口.事实上，树枝的表面是粗糙的.但是之前的研究中没有关于树枝表面粗糙度的数据，文献[21]研究得到的树枝表面粗糙度为0.002 m，将其作为参考用于代表全尺寸的树木表面粗糙度.流域中的三维微观树冠模型是由VBA生成的，其树冠中的树枝叶子是由计算机编程产生的，其外形及特征与真实树冠十分相似，每一个虚拟树冠都具有不同的随机分布结构，可近似认为本文的虚拟树冠是“真实”的，如图2所示.

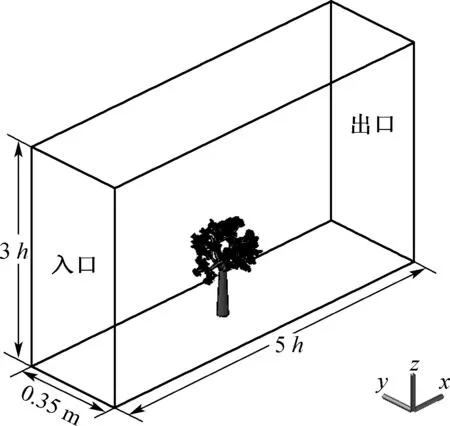
图1　树冠模型模拟的计算域和边界条件Fig.1　Computational domain and boundary conditions for simulation with model trees

图2　微观模型中的虚拟树冠Fig.2　Picture of the virtual tree used in the microcosmic model

2风洞试验

为了验证三维微观树冠模型的可行性，选取槐树树枝进行风洞试验以验证数值模拟结果.风洞试验装置和测点位置(截面A)如图3所示.风洞由有机玻璃材料制成.

1—风机；2—变频装置；3—软接头；4—孔板流量计；5—扩压器；6—蜂窝栅极；7—测试段图3　风动试验装置Fig.3　Diagram of the wind tunnel for the airflow experiment

将选取的树枝置于测试段(圆形风筒)，每种树枝设定5种不同光学孔隙率，共计进行20组试验.光学孔隙率通过控制试验树枝的数量以及叶片数来实现.光学孔隙率取值范围为0～1.根据光学孔隙率定义[22]可知，在二维水平面内，测试段7底面积与树枝叶片面积重合部分之差与测试段7底面积之比即为光学孔隙率，也可称其为疏透度，其定义：在垂直于某一水平方向上，树冠边缘垂直面上的透光孔隙的投影面积与该垂直面上的树体投影总面积之比.试验时，通过无极变频装置2(0～50 Hz内无极调节)和蜂窝栅极6均匀向测试段输送速度1.0～ 15.4 m/s的连续风.并在测试段7的B、C两点采用数字压差计测量气流通过树枝前后的压力损失，B、C两点分别在测试段圆周上均匀取6个测试点以测出A、B两点平均静压差.测试段7尾部通向大气，每变换一次风速等待片刻，待风速均匀稳定后再进行测试. 风速测量可以通过孔板流量计间接测得，也可以直接在测试段7使用热线风速仪测量.为获得更高的测量精度，本试验采用后者.

施加于植被上的全部阻力与穿过树冠内部和周围的气流流动有关，大部分由孔隙率控制.选取5组树冠模型进行二维和三维孔隙率的测量.二维光学孔隙率采用数字化扫描方法，首先取得清晰的树木照片，用数字化扫描仪把照片转化为数字化图像文件，利用树冠与背景之间的灰度差异，使用自编程计算软件计算树叶面积，求得透光孔隙面积，从而得到光学孔隙率或疏透度.三维体积孔隙率的测量使用简单的排水体积法，假设树是实心无孔隙的,然后树被拆卸，每个枝干放入一装满水的量筒中，将每个枝干体积相加得到孔隙率.在计算模型中最重要的一个参数是叶面积密度(LAD).模型中虚拟树木的LAD获得方法与光学孔隙率相似.

物体表面的阻力系数(Cd)可由式(1)确定

(1)

式中：u为风速；ρ为流体密度；p为压力.变量u、ρ可直接测量，而p必须直接测量或者通过Cd确定.为了简化几何形状，可以通过确定的阻力曲线得到Cd.

3结果与讨论

3.1树冠流场特性

采用在动量和湍流输运方程中附加源/汇项的方法模拟树冠内的绕流效应，但此方法要明确地解释树冠内各向异性的空间结构所导致的气流复杂性是不可能的.事实上，树冠内绕流的相互作用会在树冠枝干尾迹区域产生大量小范围风速减小，使用先前的传统方法无法实现这些小范围的风速减小.迄今为止，文献[21]通过在模型中引入有明确树枝结构，研究了无叶树冠的流场，预测效果良好.本文的创新之处在于，三维微观树冠模型在树枝周围增加了“真实叶子”，能够深入分析树冠结构对树冠内部及周围区域绕流流动的影响.图4(a)显示了具有树叶的树冠层内部流场速度分布图，而图4(b)显示了树冠层内部流场分布的细节图，这是先前的传统方法无法实现的.由图4可知，树冠内的风速整体是减小的，而在树枝、树叶周围和背风处的风速却是增加的.

(a) 整体速度云图，h= 2.25 m (LAD值=25.89 m-1)

(b) A处速度云图细节图

3.2孔隙率

本文使用的三维微观树冠模型的孔隙率测试结果如表1所示. 由表1可知，光学孔隙率变化范围为0.15～0.64，而体积孔隙率会大一些，其变化范围为0.93～0.96.

表1　孔隙率测试结果

图5给出了虚拟树冠的光学孔隙率和体积孔隙率的关系.由图5可知，光学孔隙率是体积孔隙率的幂函数.在文献[22]的研究基础上，将表1孔隙率分析结果进行拟合，则光学孔隙率与体积孔隙率的关系如式(2)所示.

(2)

式中:Po为光学孔隙率；Pv为体积孔隙率.

图5　微观模型的体积孔隙率与光学孔隙率关系Fig.5　The relationship between volumetric porosity and optical porosity for the microcosmic model

式(2)函数与数据的相关系数为0.805，满足实心物体模型孔隙率为0的客观要求，若无物体，光学孔隙率和体积孔隙率均为1.由式(2)可知，文献[22]总结的光学孔隙率与体积孔隙率的关系曲线的斜率明显小于本文得到的两者关系曲线的斜率，这主要是由于研究的植物结构特性及叶子的长宽比不同.文献[22]使用的是松树，其体积增长速度快于面积，因此体积孔隙率的增长比例大于光学孔隙率.而本文使用的是虚拟槐树，由于槐树叶面积较大，其面积增长速度快于体积，因此体积孔隙率的增长比例小于光学孔隙率.不仅由于叶面结构的不同，同种植被拥有不同深度和宽度比时(本文深宽比为1∶1)，幂指数都可能会改变.

3.3阻力研究

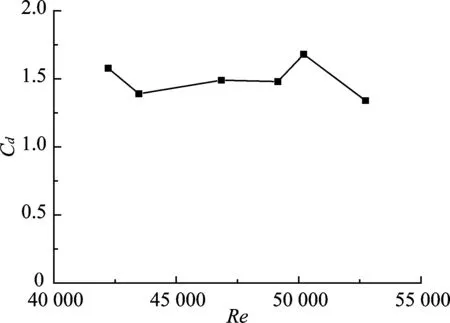
本文使用的风速范围对应的雷诺数(Re)范围为0.4×105～1.7×105，Re与Cd的关系如图6所示. 文献[16]测得实心物体的表面阻力系数为0.6.由图6可知，在本文所考虑的所有Re范围内，有孔隙的介质均比实心物体具有更大的阻力系数.随着风速的增大，Re值增大，但相同孔隙率下的每种树冠模型的阻力系数均减小.

(a) u=3 m/s

(b) u=10 m/s

different wind speed

在低Re值和高Re值下，阻力系数Cd与光学孔隙率Po的关系曲线如图7所示.

图7　光学孔隙率与阻力系数关系图Fig.7　The relationship between Po and Cd

由图7可知，随着Po从0增加到1，Cd值先增大，达到最大值后减小,直到孔隙率为1时减到0.由图7还可以明显发现，三维阻力系数随Po的变化明显不同于文献[16]总结的二维篱笆孔隙率与阻力系数的曲线关系，其二维风阻的阻力系数随着光学孔隙率增大而逐渐减小.将图7中的数据进行拟合,可得到如下关系式

1.087×10-6Re+0.843，R2=0.95

(3)

由式(3)可知，Re对Cd的影响较小，若忽略Re对关系式的影响，拟合得到

Cd=-4.46Po2+3.72Po+0.843

(4)

将不同Re值下阻力系数随光学孔隙率的关系曲线与其他文献进行对比,结果如图8所示.由图8可知，随着光学孔隙率从0增加到1，Cd均是先增大，达到最大值后减小,直到孔隙率为1时减到0.由图8中还可以明显发现，文献[22]总结的阻力系数随光学孔隙率的关系曲线中，其Cd最大值对应的光学孔隙率小于本文得到的光学孔隙率，这与图5中光学孔隙率和体积孔隙率的关系曲线相对应，其主要原因是研究的植物结构特性及叶子的长宽比不同.随着孔隙率的增加，低Re值和高Re值下的阻力系数曲线开始汇聚，这表明随着孔隙率的增加，阻力系数Cd开始独立于雷诺数Re.

图8　光学孔隙率与阻力系数关系图与其他文献对比Fig.8　The relationship between Po and Cd compared with other literature

根据文献[23]提出的树冠动量源项Su：

Su=-Cd×ρAfu2

(5)

式中：Cd为阻力系数；ρ为空气密度；Af为叶面积指数；u为空气平均流速.

树冠阻力Δp的表达式为

Δp=Cd×ρu2/2

(6)

将式(4)代入式(6)可得：

3.72Po+0.843)×ρu2/2

(7)

本文采用槐树进行试验，分别取5种光学孔隙率，则可得到5条不同光学孔隙率的压力损失-速度曲线.分别将这5条曲线所对应的光学孔隙率以及速度代入式(7)得到5条模拟曲线.但模拟公式得到的压差偏大，故需乘以修正系数k，即：

3.72Po+0.843)×ρu2/2

(8)

由此得出的模拟数据与试验数据进行对比，结果如图9所示.表2列出了5种光学孔隙率下试验数据与经过修正的模拟结果的平均相对误差.

图9　试验数据与经过修正的拟合结果对比Fig.9　Comparison of the modified simulation results and measured data

Po0.190.270.440.550.70平均相对误差/%3.902.126.043.082.78

3.72Po+0.843)

(9)

式中：k为试验修正系数，校正试验中所产生的误差，其数值为0.62～1.25.光学孔隙率小的修正系数选取较小数值，光学孔隙率大的修正系数选取较大的数值.

4结语

为深入分析三维微观树冠内部结构参数对树冠绕流流动阻力系数的影响，采用VBA程序构建复杂的三维虚拟树冠模型.采用数值模拟和试验测试相结合的方法研究不同孔隙率和风速下树冠的内部流场特征和流动阻力.用树冠叶面积密度(LAD)、光学孔隙率(Po)以及体积孔隙率(Pv)来表征树冠复杂的形态结构，提出树冠结构参数间的关联关系，并讨论树冠形态结构参数对树冠流动阻力的影响规律,并得到下述结论.

(1) 通过在流场中放置一个由VBA生成的三维虚拟树冠模型来预测树木枝干及“真实叶子”对树冠内部及周围区域绕流流动的影响，能够捕捉到空气绕流流动特性的细节，深入分析树冠结构对树冠内部及周围区域绕流流动的影响.

(2) 孔隙率的分析结果表明了光学空隙率和体积孔隙率之间的关系，尽管经过试验检验这两者间的关系可能是真实的，但不同树冠结构的光学孔隙率和体积孔隙率之间的关系有待进一步深入研究.

(3) 树冠的阻力系数与光学孔隙率满足近似二次多项式关系，故采用光学孔隙率分析树冠阻力系数，并且该多项式可以直接应用到防风林的单一树冠风阻作用的预测中.

参考文献

[1] HEISLER G M, DEWALLE D R. Effects of windbreak structure on wind flow [J]. Agriculture, Ecosystems and Environment, 1988,22(23): 41-69.

[2] MARSHALL J K. Drag measurements in roughness arrays of varying density and distribution [J].Agricultural Meteorology, 1971, 8(3): 269-292.

[3] GILLETTE D A, STOCKTON P H. The effect of nonerodible particles on wind erosion of erodible surfaces[J]. Journal of Geophysical Research, 1989, 94(10): 12885-12893.

[4] MUSICK H B, GILLETTE D A. Field evaluation of relationships between a vegetation structural parameter and sheltering against wind erosion[J]. Land Degradation & Rehabilitation, 1990, 2(2): 87-94.

[5] STOCKTON P H, GILLETTE D A. Field measurement of the sheltering effect of vegetation on erodible land surfaces[J]. Land Degradation and Rehabilitation, 1990, 2(2): 77-85.

[6] IVERSEN J D, WANG W P, RASMUSSEN K R,et al. Roughness element effect on local and universal saltation transport[J]. Acta Mechanica, 1991, 2: 65-75.

[7] RAUPACH M R. Drag and drag partition on rough surfaces [J]. Boundary-Layer Meteorology, 1992, 60(3): 375-395.

[8] RAUPACH R A, GILLETTE D A, LEYS J F. The effect of roughness elements on wind erosion thresholds[J]. Journal of Geophysical Research, 1993, 98(2): 3023-3029.

[9] NICKLING W G, MCKENNA N C. Development of deflation lag surfaces[J]. Sedimentology, 1995, 42(3): 403-414.

[10] WOLFE S A, NICKLING W G. Shear stress partitioning in sparsley vegetated desert canopies[J]. Earth Surface and Landforms, 1996, 21(7): 607-619.

[11] HAGEN L J, SKIDMORE E L. Turbulent velocity fluctuations and vertical flow as affected by windbreak porosity[J]. Transactions of the ASAE, 1971, 14(4): 634-637.

[12] SEGINER I, SAGI R. Drag on a windbreak in two-dimensional flow[J]. Agricultural Meteorology, 1971/1972, 9: 323-333.

[13] SEGINER I. Windbreak drag calculated from the horizontal velocity profile[J]. Boundary-Layer Meteorology, 1972, 3(1): 87-97.

[14] WILSON J D. On the choice of a windbreak porosity profile[J]. Boundary Layer Meteorology, 1987, 38(1): 37-49.

[15] WANG H, TAKLE E S. On three-dimensionality of shelterbelt structure and its influences on shelter effects[J]. Boundary-Layer Meteorology, 1996, 79(1): 83-105.

[16] TAYLOR P A. Flow and transport in the natural environment: Advances and applications [M]. New York : Springer-Verlag, 1988: 270-292.

[17] WANG S, TAKLE E S. A numerical simulation of boundary-layer flows near shelterbelts[J]. Boundary-Layer Meteorology, 1995, 75(1): 141-173.

[18] VOGEL S. Drag and reconfiguration of broad leaves in high winds[J]. Journal of Experimental Botany, 1989, 40(8): 941-948.

[19] GRANT R. The influence of the physical attributes of a spruce shoot on momentum transfer[J]. Agricultural and Forest Meteorology, 1985, 24: 7-18.

[20] MAYHEAD G J. Some drag coefficients for British trees dericed from wind tunnel studies[J]. Agricultural Meteorology, 1973, 12: 123-130.

[21] WIERINGA J. Updating the davenport roughness classification[J]. Wind Engineering and Industrial Aerodynamics, 1992, 41(1), 357-368.

[22] GRANT P F, NICKLING W G. Direct field measurement of wind drag on vegetation for application to windbreak design and modeling[J]. Land Degradation & Development, 1998, 9(1):57-66.[23] SANZ C. A note onκ-εmodelling of vegetation canopy air-flows [J]. Boundary-Layer Meteorology, 2003, 108(1): 191-197.

文章编号：1671-0444(2016)03-0426-06

收稿日期：2015-05-12

基金项目：国家自然科学基金资助项目(41371445)

作者简介：王冰清(1990—)，女，辽宁抚顺人，硕士研究生，研究方向为空气过滤净化与空气品质. E-mail：wbq1827@163.com 付海明(联系人), 男，高级工程师，E-mail: fhm@dhu.edu.cn

中图分类号：X 513; S 731.2

文献标志码：A

Flow Resistance Characteristics Analysis of Micro-scale Canopy

WANGBing-qinga, b,FUHai-minga, b

(a. School of Environmental Science and Engineering; b. State Environmental Protection Engineering Center for Pollution Treatment and Control in Textile Industry, Donghua University, Shanghai 201620, China)

Abstract:A three-dimensional(3D) architecture of canopy was produced by VBA (visual basic application) and CFD (computational fluid dynamics) was used to investigate the flow characteristics and flow resistance through 3D microcosmic vegetation canopies with different porosities and various velocities. Optical porosity and volumetric porosity were used to analyze the complicated morphology of vegetation canopy and influences of canopy structure parameters on flow resistance. The results show that, the relationship between drag coefficient and optical porosity can be approximately predicted as a quadratic polynomial, and a model expression is presented through simulation results. The model expression is validated using experimental results in a wind tunnel with tree branches. Based on the comparison of drag coefficient data obtained through the field experiments in real environment, this method provides a basis for predicting the real drag coefficient.

Key words:canopy; drag coefficient; porosity; microcosmic model