福建杉木树冠外轮廓和树冠体积相容性模型

吴丹子， 王成德， 李 倞， 刘 敏

（1. 北京林业大学 园林学院， 北京100083； 2. 北京林业大学 信息学院， 北京100083； 3. 北京林业大学城乡生态环境北京实验室， 北京100083）

树冠外轮廓模型是指以树木树冠任意位置处半径为因变量， 以冠幅、 冠长、 树高或胸径等因子为自变量的函数， 用来模拟树冠形状变化规律的数学表达式［1］。 树冠外轮廓模型不仅能够估计树冠任意位置处的树冠半径和推导计算整个树冠体积， 而且可以驱动林分树木树冠三维可视化模拟。 此外， 树冠形态与树冠体积对于间接估算树木树冠部分生物量具有重要意义［2］。 为了描述树冠外轮廓形态变化规律和推导计算树冠体积， 国内外学者常利用以下方法预测树冠相关变量， 包括简单几何形状模拟、 经验模型方法、 树冠轮廓模型积分法、 激光扫描方法等。 早期学者们利用规则几何体描述树冠外轮廓二维形状， 常采用如下公式定义树冠形状：RCR=（1-RDH）k， 其中：RCR表示相对树冠半径，RCH为从树冠基部到任意位置处树冠长度与最大树冠长度的比，k的取值决定了其几何形状， 当k为0、 0.5、 1.0、 1.5 时分别表示圆柱形、 抛物线形、 圆锥形或凹面形等， 该模型被广泛应用于道格拉斯杉Pseudotsuga douglasii［3］、 西部铁杉Tsuga heterophylla［4］、 火炬松Pinus taeda［5］、 华北落叶松Larix principis-rupprechtii［6］等树冠形状模拟和体积计算研究中。 PRETZSCH 等［7］、 SADONO［8］将树冠分为 “阳冠” “阴冠” 两部分， 分别采用抛物线体和圆锥体表示。 由于树冠形状并不是简单规则形式， 不同树种树冠形状并不相同， 树冠体积大小与冠幅、 冠长、 胸径、 树高等林木因子之间存在相关关系， 研究者针对不同树种利用经验模型方法构建幂函数、 指数函数等多种形式树冠体积模型， 如楠木Phoebe zhennan［9］、 樟子松Pinus sylvestrisvar.mongolica［10］、杉木Cunninghamia lanceolata［11］、 长白落叶松Larix olgensis［12］、 欧洲赤松Pinus sylvestris和云杉Picea asperata［13］、 黑荆树Acacia mearnsii［14］， 也有研究者通过构建枝条长度、 角度、 半径等枝条属性经验方程间接预测树冠半径和模拟树冠形态变化规律， 如李凤日［15］、 LI 等［16］、 GILMORE 等［17］、 姜立春等［18］， 但是存在树冠枝条测量困难且误差较大问题。 三维激光扫描等技术的发展， 不仅提供了快速数据获取方式，而且能够更加准确获取树冠数据［19-21］， 但由于数据获取成本高、 处理困难、 数据量大等限制了它的使用。 除了以上方法， 为了更加准确预测树冠体积， 一些学者利用多项式［22］、 幂函 数［23］、 修正Beta曲线［24］、 连续分段函数［25］等曲线形式描述树冠外轮廓形态， 并将树冠曲线围绕树干轴旋转得到的旋转体， 通过对旋转体积分推导计算树冠体积［26-28］。 该方法只需要简单林木因子就能够准确模拟树冠形态与树冠体积。 目前， 树冠外轮廓模型积分法计算体积研究， 一般将树冠外轮廓与树冠体积模型单独进行研究， 分别拟合不同模型方程得到2 套模型参数； 由于外轮廓与体积方程之间存在内在相关性， 采用传统最小二乘方法分别求解模型参数， 不能保证2 个模型误差同时最小， 无法满足模型参数估计的渐进无偏性、 有效性和一致性。 通过对树冠轮廓模型积分推导得到树冠体积方程， 将2 个方程联立构建一致性方程组， 能够有效解决以上模型参数估计存在的问题。 目前一致性方程组的研究主要集中在树干削度与材积一致性方程组研究方面［29-30］， 关于利用树冠外轮廓与树冠体积一致性模型方面研究还未见报道。 本研究以福建地区杉木人工林为研究对象， 采用似乎不相关回归方法， 构建以最大树冠半径与相对冠长为自变量的树冠外轮廓和树冠体积一致性方程组模型， 研究构建的模型能够用于驱动树木树冠三维可视化模拟， 直观地反映不同生长条件下树冠生长活力及林木个体间树冠重叠程度， 指导林分抚育间伐活动， 同时为通过树冠体积间接推算树冠生物量提供新思路。

1 研究区域与数据收集

福建省位于中国东南沿海地区（23°33′～28°20′N， 115°50′～120°40′E）， 地势东南低西北高， 地形多丘陵少平原， 不同区域气候相差较大， 其中东南沿海属南亚热带气候， 东北与西北区域属中亚热带气候， 年平均气温为15.0～22.0 ℃， 年平均降水量为1 400～2 000 mm， 土壤类型主要包括红土壤、 黄土壤、 山地草甸土壤， 主要用材树种有杉木、 马尾松Pinus massoniana、 巨尾桉Eucalyptus grandis×E.urophylla等。 杉木为杉科Taxodiaceae 乔木， 幼树树冠尖塔形， 大树树冠圆锥形， 为中国长江流域、 秦岭以南地区栽培最广、 生长快、 经济价值高的用材树种。

研究数据来自于福建省顺昌县大历和岚下林场布设的杉木人工纯林临时样地， 选择不同龄组、 林分密度和立地条件类型设置标准样地， 共设置98 块30 m × 20 m 的样地， 每个标准地内选择3～5 株树木，共413 株杉木。 测量每株树木胸径（D）、 树高（H）、 冠幅（CW）、 最大冠长（LCL）、 枝下高（HCB）， 树冠长度（CHi）以及相应树冠半径（CRi）， 其中：i（i=0.10、 0.25、 0.50、 0.75、 0.90）表示从树冠基部到树梢顶端的相对位置。 树冠因子测量如图1 所示， 该装置由透明绘图板、 三脚架以及照准装置组成， 具体使用方法如下： ①根据相似三角形原理， 在距离所测树冠一定距离位置处（通常距离1 倍树高）， 将该绘图板固定在三脚架之上保持板面垂直于地面， 然后通过透明板观察树冠， 往后移动三脚架， 保持透明板与地面垂直， 直到通过透明板能够观察到整个树冠。 ②用笔将树冠外轮廓绘制在透明板之上， 首先绘制树冠枝下高位置处的点A、 树冠顶端的点B以及最大树冠位置处的点C与点D， 然后从A点开始到B、C点，将树冠轮廓绘制出来。 并将透明板上的树冠轮廓草图复制到有计算网格方格的透明硫酸纸上。 ③利用测高仪器和皮尺分别测量该树冠的冠长L（LCL=A′B′）和冠幅（CW=E′F′）， 计算树冠冠长测量值A′B′与绘图纸上AB之间比值以及树冠冠幅测量值E′F′与CD之间比值， 根据这2 个比值在绘图纸上分别计算树冠冠长0.10、 0.25、 0.50、 0.75、 0.90 位置处对应的树冠长度和半径值。 为了尽可能减少树冠测量误差， 应从多个方向观察树冠， 取测量均值。 通过以上调查方法收集到杉木树冠调查数据情况如表1 所示。

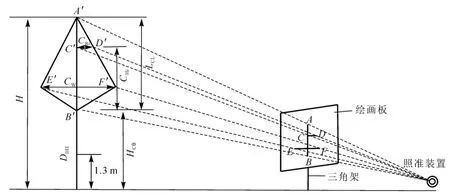
图1 杉木树冠测量因子示意图Figure 1 Schematic diagram of crown measurement factors of C. lanceolata

表1 树冠调查数据的基本概况Table 1 Summary statistics of measurements of tree variables

2 研究方法

2.1 树冠外轮廓模型与体积模型

本研究收集整理了国内外文献研究中常用于描述树冠外轮廓形状的模型方程， 具体形式如模型1、模型2、 模型3 以及模型4 所示。 其中： 模型1 被广泛用于模拟多个树种树冠形态［3］， 该模型是否可用于杉木树冠模拟需要进一步验证， 其他3 个模型常用于模拟杉木树冠［23］。 本研究将这4 个可积分模型方程作为联立方程组中树冠外轮廓模型的备选模型。 模型因变量为任意位置处树冠半径（CR）， 模型自变量为相对树冠冠长（RCH）、 最大树冠半径（LCR）。

采用积分法计算树冠体积， 从树冠基部到树木顶端积分树冠外轮廓模型， 得到体积方程， 其中：VC为树冠体积，LCL最大树冠长度，CH为从树冠基部到树冠任意位置处树冠长度， 推导得出树冠体积模型方程。

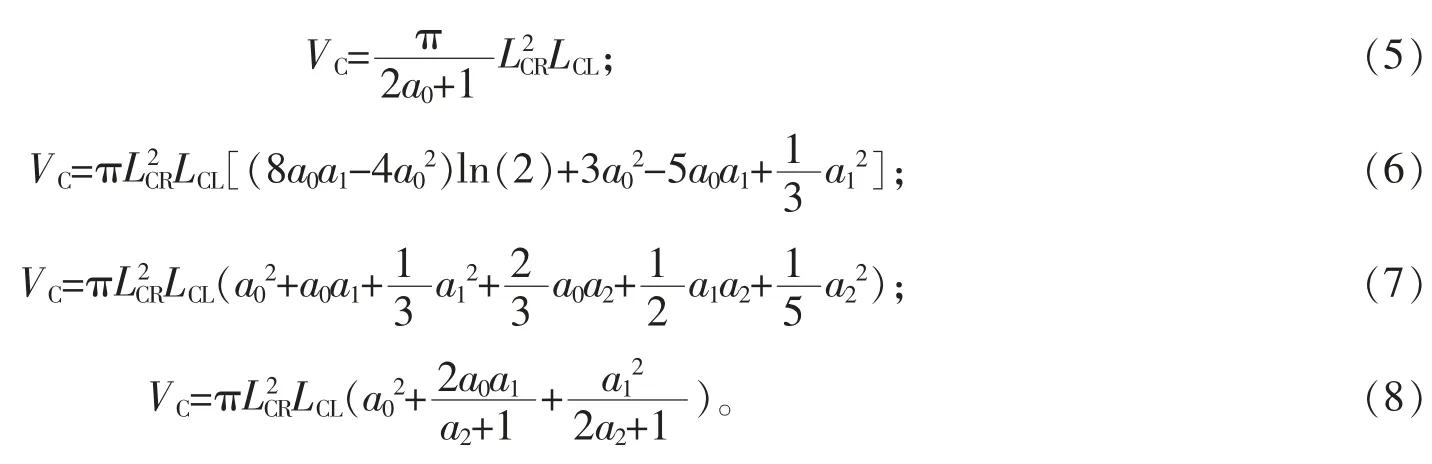
式（5）～（8）中：RCH为相对冠长（RCH=CH/LCL， 树冠基部为0， 树冠顶部为1）；a0、a1、a2为模型系数。

2.2 似乎不相关非线性模型

假设定义如下非线性模型联立方程组， 存在一组随机变量Y1， …，Yn与自变量x1， …，xn之间满足非线性关系， 如下：

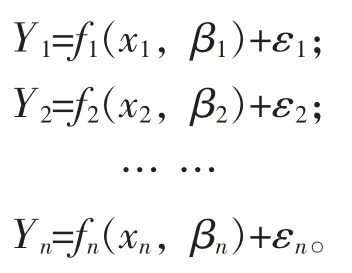
其中：n个模型的同一次观测模型误差εi的各分量间是相关的， 即cov（εi）是非对角矩阵［17］。 这里多个方程之间存在联系， 各方程的扰动项之间存在相关性， 同时估计多个方程能够提高模型估计效率。

将树冠外轮廓模型和树冠体积模型两两联立为方程组， 即2.1 中式（1）与式（5）、 式（2）与式（6）、 式（3）与式（7）、 式（4）与式（8）共4 个方程组。 每组的2 个方程拥有同一套参数， 对2 个模型共同进行拟合， 即解决非线性联立方程组模型的参数估计问题。

为了保证参数估计的一致性和渐进无偏性， 利用SAS 统计软件proc model 程序提供的似乎不相关回归法（SUR）， 选择SUR 法同时拟合树冠外轮廓与体积相容性模型。 此外， 在林业模型拟合过程中， 模型误差项之间可能存在异方差的问题， 本研究采用模型回归函数自身作为权函数消除异方差［13］。

2.3 模型评价和检验指标

模型拟合和检验结果通过以下指标评价： 决定系数（R2）、 均方根误差（RMSE）和平均绝对误差（MAE）、平均偏差（MD）。 最优模型选择根据R2最大，RMSE、MAE、MD绝对值最小的原则进行。 具体公式如下：

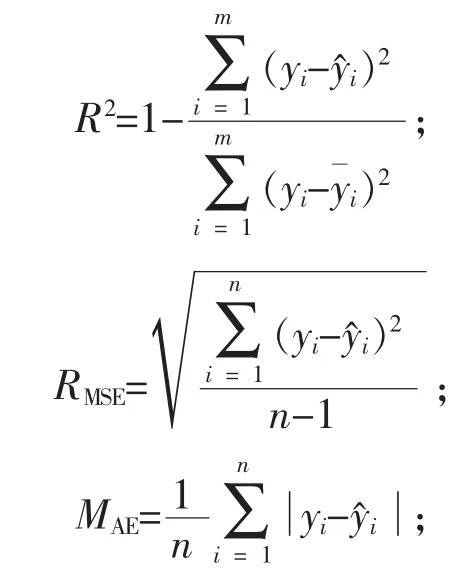
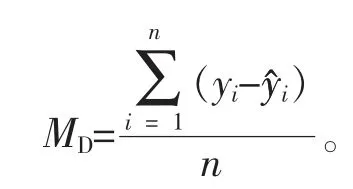
其中：yi为第i因变量实际值， y＾i为第i因变量预测值，yi为因变量实际值平均，n为样本数。

3 结果与分析

3.1 平均断面积求积法

树冠体积数据可采用分层切割法处理得到。 本研究在对杉木树冠进行调查时， 采用平均断面积求积法， 将树冠从树梢到树冠基部按照相对冠长分6 部分（0～0.10， 0.10～0.25， 0.25～0.50， 0.50～0.75， 0.75～0.90， 0.90～1.00）。 将树冠最上部分看作圆锥体近似计算体积， 其他各部分采用平均断面积法。 计算公式如下：

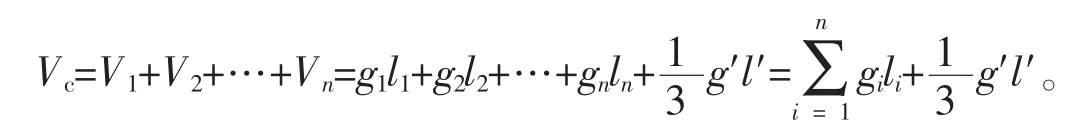
其中：Vc表示整个树冠体积（m3）；Vi为第i部分树冠体积（m3）；gi为第i区分段中央断面积（m2）；li为第i分段长度（m）；g′为梢头底端断面积（m2）；l′为梢头树冠长度（m）；n为分段个数。

3.2 树冠外轮廓-体积一致性方程系统的总体评价

利用SAS 软件的proc model 模块中似乎不相关回归过程SUR 方法对树冠外轮廓模型和树冠体积预测模型的一致性方程组同时进行拟合， 表2 给出了不同模型拟合的统计量， 即决定系数（R2）、 均方根误差（RMSE）。

表2 树冠外轮廓-体积模型拟合结果Table 2 Fitting results of crown profile and crown volume models

由表2 拟合结果可知： 树冠外轮廓模型拟合指标R2的对比结果为模型4＞模型3＞模型2＞模型1，轮廓模型拟合指标RMSE的对比结果为模型4＜模型3＜模型2＜模型1， 树冠体积模型拟合指标R2的对比结果为模型4=模型3＞模型2＞模型1， 体积模型拟合指标RMSE结果为模型4＜模型3＜模型2＜模型1。 根据R2最大且RMSE相对较小的最优模型选择标准， 不管从树冠外轮廓还是体积模型结果来看， 模型4 显示了较好的拟合结果， 最终利用模型4 来描述福建地区杉木树冠外轮廓和树冠体积。

3.3 相容模型检验

建模数据只能反映模型拟合的好坏， 不能反映模型的预测性能。 模型系统的独立性检验是采用建模时未使用的独立样本数据， 对各模型系统的预测性能进行综合评价。 基于表3 的参数估计值和检验数据， 利用SAS 软件计算各模型系统树冠外轮廓和体积的绝对误差、 均方根误差。 从表3 可以看出： 各树冠外轮廓模型的检验指标R2对比结果为模型4＞模型3＞模型2＞模型1， 外轮廓模型RMSE对比结果为模型4＜模型3＜模型2＜模型1， 各树冠体积模型检验指标R2对比结果为模型3=模型4＞模型2＞模型1， 体积模型RMSE对比结果为模型4＜模型3＜模型2＜模型1， 不管是从R2还是RMSE来看， 模型4均优于其他模型。 此外， 模型4 的检验指标MAE和MD绝对值最小， 真实值与预测值之间误差最小， 进一步验证了模型4 作为杉木树冠外轮廓-体积模型的合理性。

3.4 模型残差图评价

模型拟合的总体评价反映了总体树冠外轮廓和体积的变化， 不能反映各模型是否存在异方差性和无偏性， 评价这2 个指标最直观的方法就是利用残差分布图。 为全面评价模型4 效果， 分别绘制模型4 加权前后的残差分布图。 图2 为未增加权函数时相容模型的残差图， 左侧为树冠外轮廓模型残差分布， 右侧为树冠体积模型残差分布， 从图2 可以看出： 残差均存在明显喇叭口形状， 说明异方差问题显著。 图3 为增加权函数后相容模型残差分布图， 从图3 可以看出： 加权后模型的残差散点图分布变得均匀， 说明权函数明显消除了异方差。 进一步说明加权后模型4 显示了较高的等方差性和无偏性， 效果较好。

表3 不同模型独立性检验Table 3 Validation results of different crown models

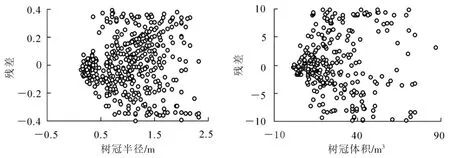
图2 未加权的SUR 方法拟合的相容模型残差分布图Figure 2 Residual distribution of models fitted by unweighted SUR method

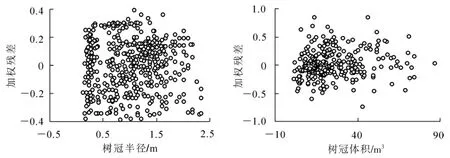
图3 加权的SUR 方法拟合的相容模型残差分布图Figure 3 Residual distribution of models fitted by weighted SUR method

4 结论

在树冠模型研究方面， 许多学者利用规则几何体模拟树冠形状并计算树冠体积， 这类方法具有简单方便特点， 但是不灵活且预测精度相对较低。 本研究以福建杉木为研究对象， 选择4 种常用的树冠外轮廓经验模型模拟树冠形状曲线， 与简单几何体模拟方法相比， 能够更加准确合理地描述树冠形状的变化， 而且方程形式更加灵活。

本研究通过树冠外轮廓模型方程推导树冠体积方程， 构建一致性的相容的非线性树冠外轮廓-体积联立方程组模型， 利用SAS 软件模块中的似乎不相关回归过程（SUR）解决复杂分段联立方程组模型系统的参数同时估计， 确保了2 个方程参数估计的一致性， 模型预测效果较好。 本研究构建的树冠外轮廓-体积一致性模型方程， 可以预测树冠外轮廓形态， 驱动林分树木三维可视化并预估树冠体积， 实现了树冠外轮廓与体积模型之间互相推导， 同时也为进一步估测树木地上部分生物量提供了理论依据。