异龄混交择伐林均衡曲线的组合应用1)

陈泽任　李昀　张青　亢新刚　张玉环　　　杨英军　王全军

(北京林业大学，北京，100083)　　　　　　　　　　　　　　　(吉林省汪清林业局)



异龄混交择伐林均衡曲线的组合应用1)

陈泽任李昀张青亢新刚张玉环杨英军王全军

(北京林业大学，北京，100083)(吉林省汪清林业局)

摘要根据异龄混交择伐林均衡状态直径结构呈现反“J”型分布的特点，利用Kolmogorov-Smirnov检验，得出吉林省汪清林业局金沟岭林场2大区5个小区树木的直径分布均满足负指数分布。利用负指数函数将Schütz均衡模型和López预测矩阵模型进行组合，组合模型同时考虑到了竞争因子等限制因素，且预测结果的相邻径阶的立木株数比率q值分布在1.2～1.5。结果表明：基于负指数函数的组合模型有效的利用了Schütz均衡模型和López预测矩阵模型的优点，既充分考虑了林分的真实情况，又优化了直径分布，保证了预测结果的稳定性，得出了较为合理和稳定的均衡曲线，进而得到较为稳定统一、均衡的林木株数分布。

关键词异龄混交择伐林 ；均衡曲线；负指数函数

由于不合理采伐以及经营管理手段落后，天然林面积急剧减少，因此，积极保护天然林，研究近自然经营，实现低产人工同龄林向异龄林的改造，充分发挥森林在改善生态环境方面的特殊功能，具有实际价值和意义[1-2]。

从生态角度出发，按可持续经营原则，对现有低产人工林实行科学的择伐经营，将其改造成异龄—混交—复层—多树种的近自然状态，既实现定期的经济收入，又取得良好的森林生态和社会服务目标[3]。利用择伐林的均衡曲线理论可以建立一套实现上述目标的经营方案。研究表明，择伐林在小块面积林地上，林型将达到结构均衡状态，描述这种状态的曲线被称为均衡曲线[4]。择伐林的均衡曲线是指在一定的条件下，随着时间的推移，通过保持一个给定的收获策略，达到稳定且不随时间变化的直径分布曲线[5]。

择伐林均衡曲线的确定方法，在德国和瑞士针对异龄择伐混交林已有大量研究，近年来开始将其用于低产人工纯林近自然改造经营[6-10]。张玉环等[11]对3种均衡模型进行了对比分析，总结了3种均衡曲线模型的差异：De Liocourt均衡模型从数学的角度描述了林木株数与径级的关系，这个模型是一个理想状态的均衡曲线，没有考虑生物学基础和经济效益；Schütz均衡模型考虑了树木的生长情况、林分的采伐策略及树木的枯损信息，能较好的描述林分的真实情况，但该模型要求林分的生长量和采伐策略具有统计规律性，并且预测结果受采样的数据影响较大；López预测矩阵模型考虑了树木的生长和进界信息，但是该模型假定没有采伐计划或者要求各个径级的采伐比率是一样的，因此，描述的真实性不如Schütz均衡模型。由于不同模型考虑的因素不同，对于同一块样地，得出的均衡株数存在差异，这使得在实际操作中无法确定使用何种均衡模型来指导实践。考虑到De Liocourt均衡模型的局限性，本文结合后两种模型的不同优势，利用负指数函数将Schütz均衡模型和López预测矩阵模型进行组合，来调和二者的差异，从而实现均衡株数的一致性。同时，在建立年直径生长量方程时，将“高径级累积断面积之和(Gcum)”作为竞争因子引入模型。

1数据概况

本文采用了吉林省汪清林业局金沟岭林场(2大区5个小区共计162块固定样地)的数据。金沟岭林场位于吉林省汪清县境内东北部，属长白山系老爷岭山脉雪岭支脉。地貌属低山丘陵。该地受季风型气候影响，平均气温3.9 ℃；降水量600～700 mm，生长期120 d。主要树种有:云杉(Picea koraiensis Nakai)、冷杉(Abies fabri)、红松(Pinus koraiensis Sieb.et Zucc.)、椴树(Tilia tuan Szyszyl)和枫桦(Betula dahurica)等[12]。该区域择伐周期为5 a，采伐时，采伐前后各调查1次，若未实施采伐，则每隔2 a进行1次复查。每块样地面积为0.04 hm2(20 m×20 m)。各小区信息见表1，对各测量年份的径级分布进行了绘图(见图1)。从图1可知，径级分布呈现出典型的反“J”型分布。利用负指数函数对5个小区各年份的径级分布进行拟合，并进行Kolmogorov-Smirnov检验，得出相应的p值(见表2)。从表2中可以看出，p值均大于置信度0.05，可见5个小区的直径分布均符合负指数分布。

表1　金沟岭林场2大区5个小区信息

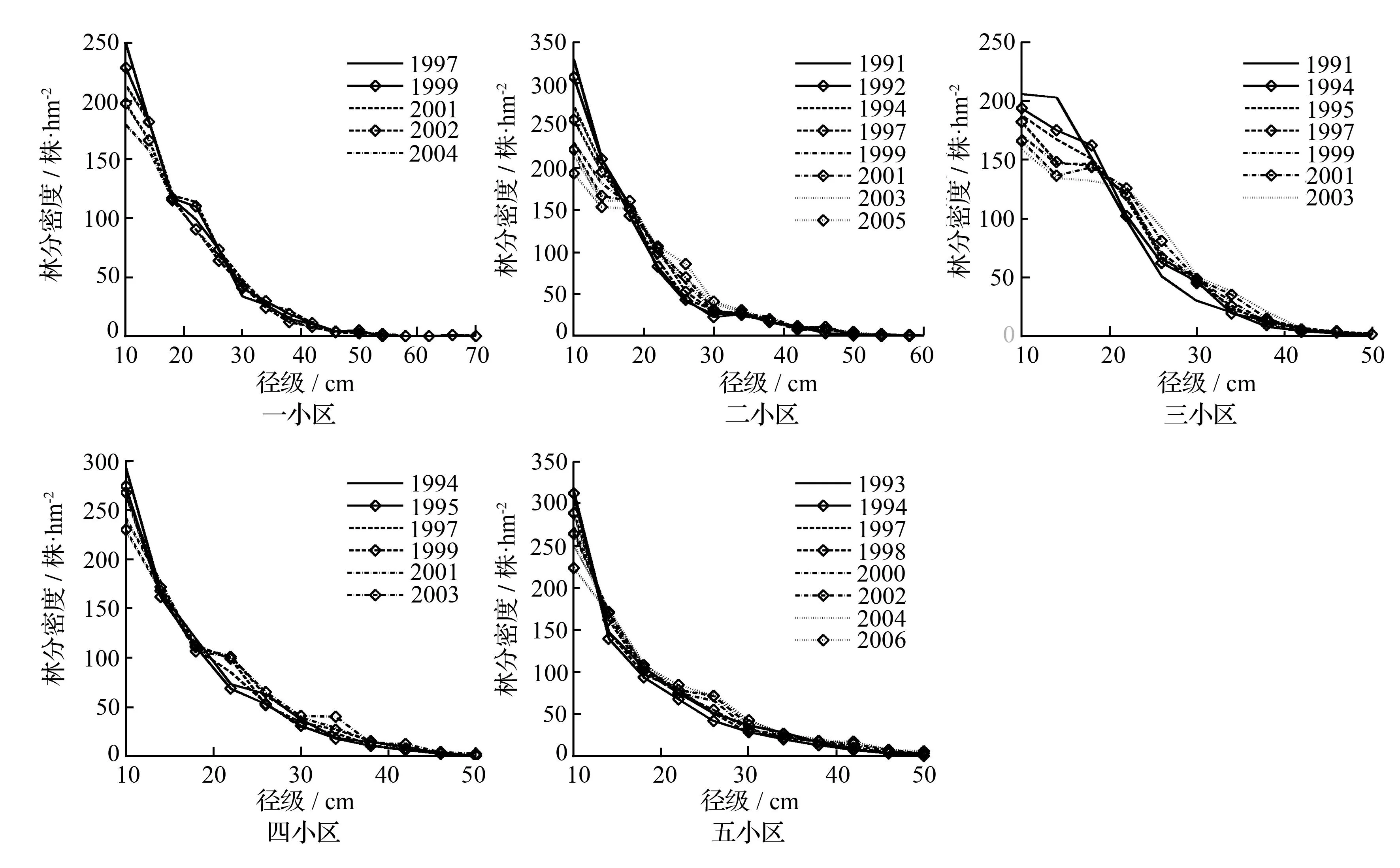
图1　各小区各测量年份径级分布图

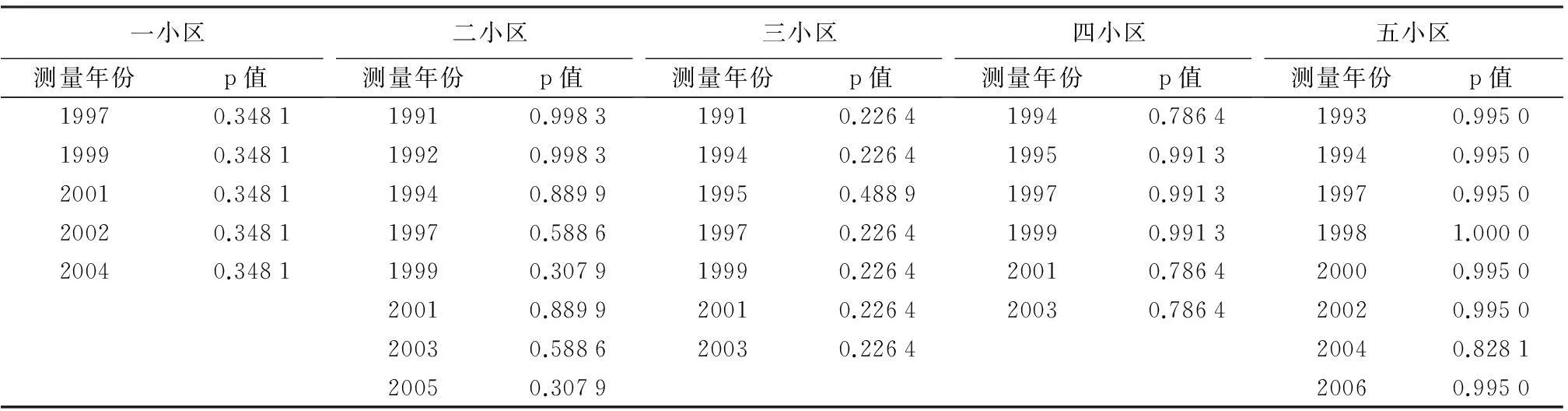
一小区测量年份p值二小区测量年份p值三小区测量年份p值四小区测量年份p值五小区测量年份p值19970.348119910.998319910.226419940.786419930.995019990.348119920.998319940.226419950.991319940.995020010.348119940.889919950.488919970.991319970.995020020.348119970.588619970.226419990.991319981.000020040.348119990.307919990.226420010.786420000.995020010.889920010.226420030.786420020.995020030.588620030.226420040.828120050.307920060.9950

2研究方法

Meyer[13]认为近天然异龄林趋于一个可用负指数方程表达的径级结构。因此，本文利用Schütz均衡模型和López预测矩阵模型预测观测样地均衡状态株数，并用负指数函数对二者进行组合。

2.1Schütz均衡模型

Schütz均衡模型假定当林分结构处于稳定状态时，如果每一个径级，从低一径级转移到此径级的株数与从此径级转移的株数和采伐株数之和相等，那么林分结构可以达到均衡状态[7]。年采伐率方程ei=f(di)，描述了择伐周期内年采伐株数(含枯损)占总株数的比例；年直径生长量方程id=f(di,Gcum)，描述了径级生长量id、径级中值di以及竞争因子Gcum(大于该径级的累积断面积之和)的关系。通过上述两个方程，第i径级的株数ni计算公式如下：

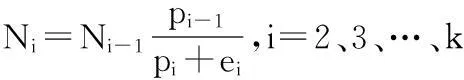
其中转移概率pi表示从i径级进入到i+1径级的概率(pi=id/dw，dw为径级宽度)。样地最小径级的株数n1是唯一需要被定义的参数。

2.2López预测矩阵模型

由于树木的进界值大小关系到再生的连续性，进而影响径级分布的稳定性。López预测矩阵模型基于人口矩阵模型，将年龄阶段替换为径级来预测可持续的采伐率和稳定的直径分布，考虑进阶值，提出了预测矩阵模型[14-15]。根据张玉环的研究[11]，模型表示如下：

式中：其中Ni(t)表示t时刻第i径级的总株数，Hi(t)=Ni(t)·hi，hi表示第i径级的年采伐率，转移概pi表示从i径级进入到i+1径级的概率，R(t)表示t时刻的进界值，该值受林分竞争激烈程度的影响。在林业中衡量竞争激烈程度的指标可用大于该径级的株数表示，即：R(t)=r2N2(t)+r3N3(t)+…+rkNk(t)。其中rk表示幼树的补充系数，k表示径级总个数。

2.3负指数函数

一般认为，典型的天然异龄林的直径分布呈指数分布，负指数函数常作为标准用于择伐作业体系下天然林结构的比较分析[12]。郑丽凤等[16]、Van Laar et al[17]推荐此函数作为异龄林的直径分布模型。因此，根据两种均衡模型的特点，利用负指数函数将二者进行组合，进而优化预测结果。

负指数函数方程Ni=a×e-bdi。式中：Ni是第i径级林木株数；di是第i径级中值；a、b为参数，a表示林分的相对密度，b表示林木株数在连续径阶中减少的速率。a值越大，说明林分总体密度越大，b越大，说明林木株数随胸径增加而迅速下降，小树的密度较大[18-19]。

3结果与分析

3.1直径生长量方程拟合结果

由图2可知，年直径生长量和径级的关系是随着径级增大，年直生长量呈现波动中增大的整体趋势。从图中可以看出，在小径级处，不同年份的直径生长量变化比较一致；在大径级处，因立木株数较少，且没有考虑树种的影响，不同年份直径生长量变化方差较大，点的分布相对比较分散。

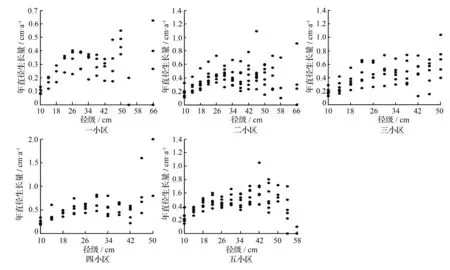
图2　年直径生长量随径级的分布

高径级累积断面积之和是一个竞争指数，它是直径大于某径级立木的所有立木断面积的总和。由图3可知，生长量的整体趋势是随着高径级累积断面积的增大而减小。

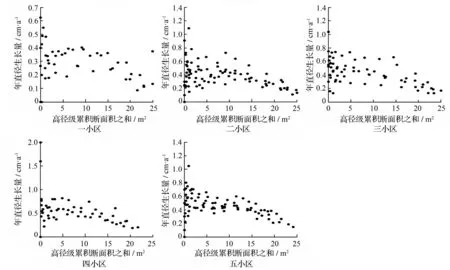
图3　年直径生长量随高径级累积断面积之和的分布

利用回归模型，拟合效果最好的年直径生长量方程为：id=b0+b1×ln(di)+b2×(Gcum)3。其中：id为年直径生长量；di为径级中值；Gcum为高径级累积断面积之和。

取显著性水平Sig.小于0.05，求得参数b0均为0，b1和b2如表3所示。

3.2年采伐率方程拟合结果

由图4可知，年采伐比率随着径级的增大先减小后增大的整体趋势。这是由于小径级处树木枯损较大，大径级处采伐较大。

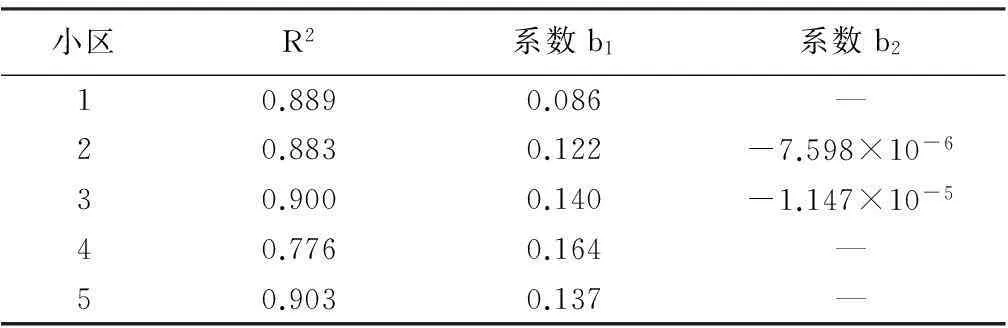
表3　年直径生长量方程拟合信息

注：1、4、5小区Gcum因子不显著，故拟合年直径生长量方程未加入该因子。

图4　年采伐率随径级的分布

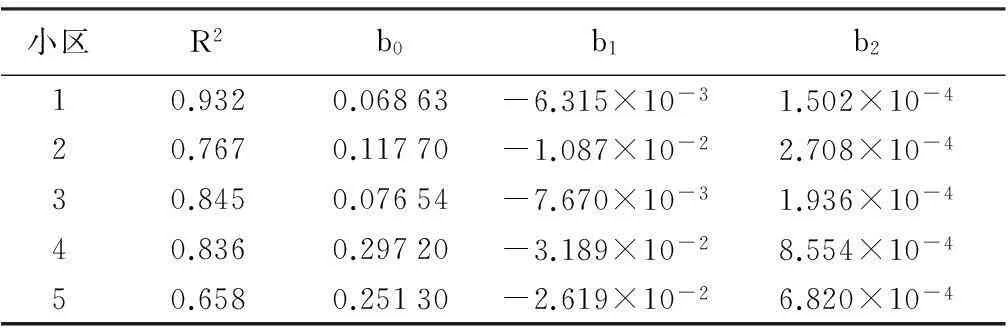
小区R2b0b1b210.9320.06863-6.315×10-31.502×10-420.7670.11770-1.087×10-22.708×10-430.8450.07654-7.670×10-31.936×10-440.8360.29720-3.189×10-28.554×10-450.6580.25130-2.619×10-26.820×10-4

3.33种均衡模型的求解

利用Schütz均衡模型和López预测矩阵模型，分别对5个小区的观测数据进行拟合，求得各小区的均衡曲线。利用负指数函数对两种均衡模型的结果进行拟合，得到的3个均衡曲线如图5所示。由图5可知，3种均衡模型求解的均衡曲线均呈现反“J”型的趋势。Schütz均衡模型的曲线存在凸起，这是由于该模型求解的采伐率随径级先减小后增大，因此，在中径级处Schütz均衡模型求解的均衡株数数值较大，均衡曲线位置较高。由于López预测矩阵模型要求各径级的采伐比率是一样的，所以其均衡曲线较匀滑。但是由于中径级处与实际情况相差较大，所以导致了在中径级(18～34 cm径级)处均衡株数较少，均衡曲线位置偏低。

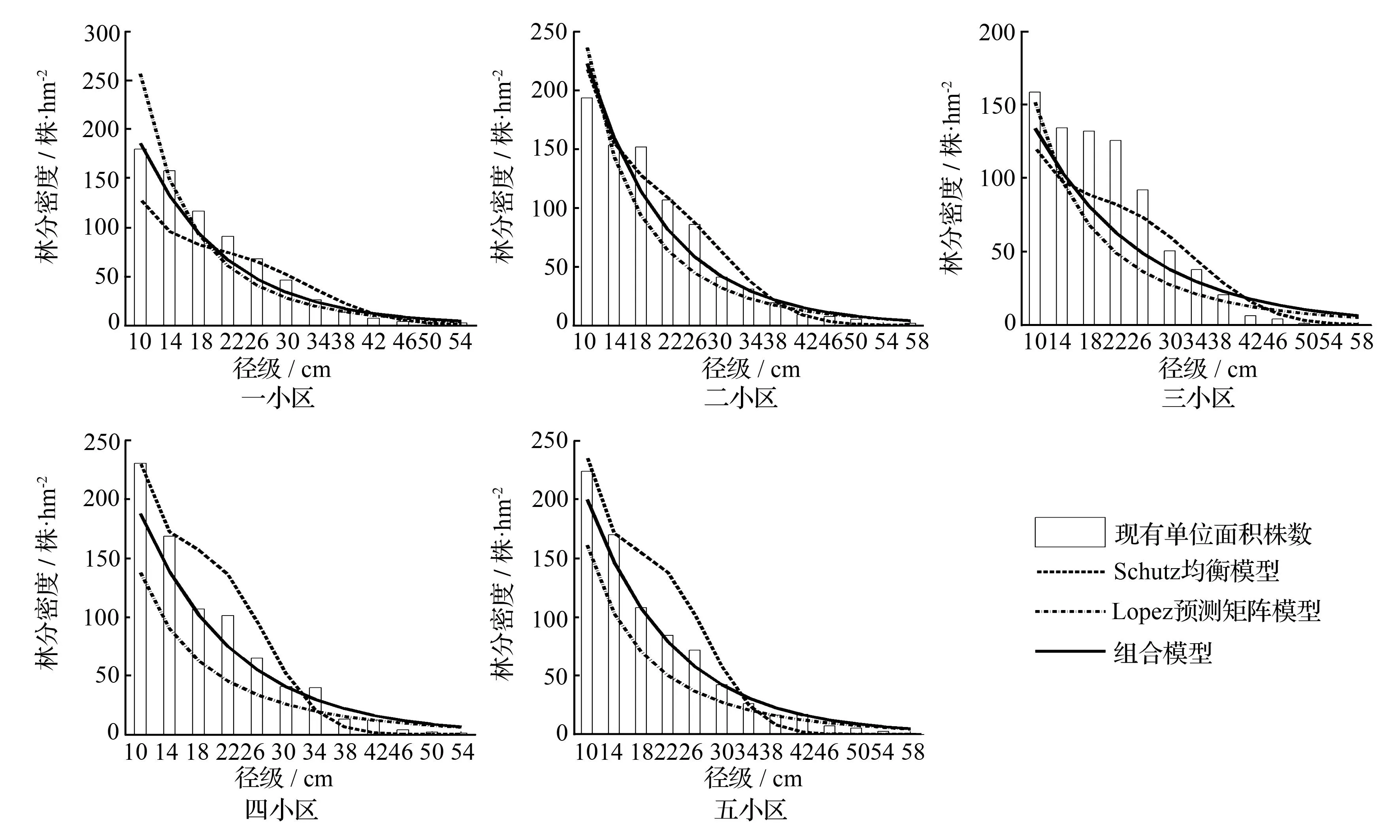
图5　现有观测株数分布与3种均衡模型预测的均衡曲线对照

De Liocourt研究表明，在典型的异龄林林分内，相邻径阶的立木株数比率(q)应为定值，q值一般在1.2～1.5；于政中[20]认为云冷杉针阔混交林q值在1.2～1.4都属于正常情况。由表5可知，Schütz均衡模型和López预测矩阵模型的q值跨度大于这个范围，不稳定。利用负指数函数将上述两种均衡模型进行组合后，q值控制在1.2～1.5，优化了直径分布，得出了较为稳定的株数分布。

表5　均衡模型的q值

4结论

本文根据择伐林均衡状态下的直径结构呈现反“J”型分布的特点，利用Kolmogorov-Smirnov检验，得出吉林省汪清林业局金沟岭林场2大区5个小区树木的直径分布均满足负指数分布。本研究建立了利用负指数函数将Schütz均衡模型和López预测矩阵模型进行调和的组合模型。模型同时考虑到了竞争因子(高径级断面积之和)等限制因素。通过对比Schütz均衡模型、López预测矩阵模型以及组合模型的预测结果，发现Schütz均衡模型和López预测矩阵模型的相邻径阶的立木株数比率q值跨度较大，而组合模型预测结果的q值分布在1.2～1.5之间，分布区间较为合理。组合模型有效的利用了Schütz均衡模型和López预测矩阵模型的优点，既充分考虑了林分的真实情况，又优化了直径分布。组合模型保证了预测结果的稳定性，得出了较为合理和稳定的均衡曲线与较为稳定统一的均衡株数分布。

参考文献

[1]吴瑶.“近自然林业”的红松林种群结构及土壤化学性质的研究[D].哈尔滨:东北林业大学,2007.

[2]吴瑶,李凤日,秦凯伦,等.近自然经营技术对红松林土壤化学性质的影响[J].东北林业大学学报,2014,42(1):76-79.

[3]谢哲根,于政中.国外异龄林经营管理研究综述[J].华东森林经理,1997,11(1):45-49.

[4]MEYER H A.Structure, growth, and drain in balanced uneven-aged forests[J].Journal of Forestry,1952,50(2):85-92.

[5]STERBA H.Equilibrium curves and growth models to deal with forests in transition to uneven-aged structure-application in two sample stands[J].Silva Fennica,2004,38(4):413-423.

[6]DE LIOCOURT F.De l’aménagement des sapinières[J].Bulletin de la Société forestière de Franche-Comté et Belfort,1898,4:396-409.

[7]SCHÜTZ J P.Modelling the demographic sustainability of pure beech plenter forests in Eastern Germany[J].Annals of Forest Science,2006,63(1):93-100.

[8]LESLIE P H.On the use of matrices in certain population mathematics[J].Biometrika,1945,33(3):183-212.

[11]张玉环,张青,亢新刚,等.异龄针阔混交择伐林均衡曲线的确定方法：以金沟岭林场样地数据为例[J].北京林业大学学报,2015,37(6):53-60.

[12]胡云云,闵志强,高延,等.择伐对天然云冷杉林林分生长和结构的影响[J].林业科学,2011,47(2):15-24.

[13]MEYER H A.Forest mensuration[M].Pennsy Lvania: Penns Valley Publishers INC,1953.

[14]OSHO J S A.Matrix model for tree population projection in a tropical rain forest of south-western Nigeria[J].Ecological Modelling,1991,59(3/4):247-255.

[15]PHILLIP J V M, NATHAN L S.The accuracy of matrix population model projections for coniferous trees in the Sierra Nevada, California[J].Journal of Ecology,2005,93(4):737-747.

[16]郑丽凤,周新年,胡喜生,等.择伐作业体系下天然林直径分布[J].东北林业大学学报,2009,37(9):22-24.

[17]VAN LAAR A, AKCA A.Forest mensuration[M].Gottingen: Cuvillier Verlag,1997.

[18]周新年,陈辉荣,游航,等.基于时间序列的天然林林分直径分布预测模型[J].福建林学院学报,2013,33(4):298-304.

[20]于政中.森林经理学[M].北京:中国林业出版社,1993:47-95.

第一作者简介：陈泽任，女，1989年10月生， 北京林业大学信息学院，硕士研究生。E-mail：chenzeren@bjfu.edu.cn。 通信作者：李昀，北京林业大学信息学院，副教授。E-mail：liyun@bjfu.edu.cn。

收稿日期：2015年10月20日。

分类号S758.5

Combined Application of Equilibrium Curve for Uneven-aged Mixed Selection Forest//

Chen Zeren, Li Yun, Zhang Qing, Kang Xingang, Zhang Yuhuan(Beijing Forestry University, Beijing 100083, P.R.China); Yang Yingjun, Wang Quanjun(Wangqing Forestry Bureau)//

Journal of Northeast Forestry University，2016,44(7)：23-27,33.

Because of the diameter structure with the characteristics of reverse ‘J’ type distribution in an uneven-aged mixed selection forest, the tree diameter distribution of five cells in the second Region in Jingouling Forest Farm of Jilin Province can be fitted by negative exponential function, which was verified by Kolmogorov-Smirnov test.A combination model, based on negative exponential function, was established by combining Schütz’s equilibrium model and López’s projection matrix model, and the combination model considered the limiting factors, such as competitive factor.The ratio q between adjacent diameter classes of predicted results ranged from 1.2 to 1.5.The combination model both took full account of the real situation stands, and optimized the diameter distribution, obtained reasonable equilibrium curve, and got a more stable distribution of tree number.

KeywordsUneven-aged mixed selection forest; Equilibrium curve; Negative exponential function

1) 国家林业局“948”项目(2013-4-66)。

责任编辑：王广建。