径流式水电厂实时优化调度系统研发
肖 杨,邝录章
(五凌电力有限公司,湖南长沙410004)
径流式水电厂实时优化调度系统研发
肖杨,邝录章
(五凌电力有限公司,湖南长沙410004)
摘要:为满足水电厂实时调度需要,构建了以发电量最大为目标的径流式水电厂实时优化调度模型,采用离散动态规划法逐步逼近寻优计算,开发出径流式水电厂实时优化调度系统。该系统可预报计算未来24 h的入库流量过程,并可实时滚动计算满足约束条件的未来24 h内各时段最优发电运行过程,从而量化指导水电厂实时优化调度。通过对6座径流式水电厂的应用,入库流量计算准确率达98%以上,平均每年可优化增加发电量4 500万kW·h。
关键词:径流式水电厂;实时优化调度;离散动态规划法
1工程概况
由五凌电力有限公司(以下简称“五凌电力”)开发建设、运行管理的沅水、资江、湘江上12座水电站已全部接入远程集中控制运行,如何提高水能利用效率,创新水库调度工作,创造最大的发电效益,成为水电厂运行管理及水库调度研究的重点。目前,尽量抬升运行库水位、降低发电耗水率的水库运行思维已成为运行调度人员的共识,但如何具体量化调度期内各时段的库水位及出力值,使得发电效益最大,亟需在实际生产运行中深入研究。
水库优化调度理论研究已较为成熟,但须将理论成果转化为生产实践[1]。本文结合以往理论研究[1-7],根据流域水库生产运行实际,以调度期内发电量最大为目标,在满足约束条件下,采用离散动态规划法,开发径流式水电厂实时优化调度系统,以期计算来水过程,实时得出水库最优运行过程,为五凌电力集中控制运行的各径流式水电厂提供量化的指导依据。五凌电力所属径流式水电厂设计运行参数见表1。
2模型构建
2.1目标函数
以日为调度周期,小时(或30min、15min)为计算时段,在已知水电站水库入流过程的条件下,求水电站出力过程和相应的水库蓄泄状态变化过程,使调度周期内的发电量最大(现已取消丰枯、峰谷电价)。其目标函数为
(1)
表1各径流式水电厂设计运行参数
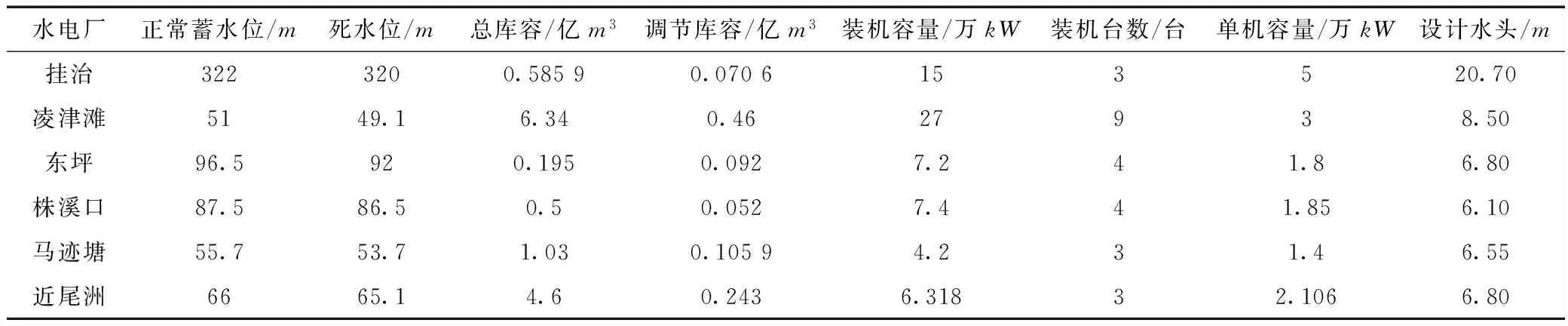
水电厂正常蓄水位/m死水位/m总库容/亿m3调节库容/亿m3装机容量/万kW装机台数/台单机容量/万kW设计水头/m挂治3223200.58590.0706153520.70凌津滩5149.16.340.4627938.50东坪96.5920.1950.0927.241.86.80株溪口87.586.50.50.0527.441.856.10马迹塘55.753.71.030.10594.231.46.55近尾洲6665.14.60.2436.31832.1066.80
式中 ,E为水电站调度期内的总发电量,kW·h;Ni为i时段电站的出力,kW;Δt为时段长度,s;T为调度期的总时段数;qi为第i时段的发电流量,m3/s;ρi为第i时段的平均耗水率,m3/kW·h。其中,ρi=f(Hi),Hi=Z上i-Z下i,Z下i= f(qi),Z上i=f(Vi),Vi=Vi-1+(Qi-qi)Δt。式中 ,Hi为第i时段的水头,m;ρi=f(Hi)为由水头查耗水率;Z上i为第i时段库水位,m;Vi为第i时段库容,m3;Z上i=f(Vi)为由库容查库水位;Z下i为第i时段尾水位,m;Z下i=f(qi)为由出库流量查尾水位;Qi为第i时段入库流量,m3/s。
2.2约束条件
(1)水量平衡约束:Vi=Vi-1+(Qi-qi)Δt
(2)
(2)机组出力约束:Nmin≤Ni≤Nmax
(3)
(3)发电流量约束:qmin≤qi≤qmax
(4)
(4)水位约束:Zmin≤Z上i≤Zmax
(5)
式中,Nmin为机组限制最小出力(各单机最小限制出力之和),kW;Nmax为机组限制最大出力(各单机最大限制出力之和),kW;qmin为最小发电流量,m3/s;qmax为最大发电流量,一般为各单机最大过流量之和,m3/s;Zmin为限制最低库水位,一般取死水位,m;Zmax为限制最高库水位,一般取正常蓄水位,m。
3计算方法
3.1目标函数的求解方法
目标函数的优化求解采用离散动态规划法[7- 8]逐步逼近寻优计算,其计算分为两个过程:
(1)初始调度线选取。首先初选步长ΔZ1,通过动态规划法求得初始优化调度线{Z0(0),Z1(0),…,ZT(0)}。
(2)优化调度计算。在初始优化调度线上各取若干个增量ΔZ2,形成一个库水位廊道,除最初、最末时段外,其余各时段形成3条调度线。用动态规划法求得该廊道内的优化调度线{Z0(1),Z1(1),…,ZT(1)}。如果该优化调度线各点均落在廊道内的非边界点上,或者虽在边界点上但却是该时段末(初)所允许的最大(小)水位,则该调度线即为所求最优解。否则,在{Z0(1),Z1(1),…,ZT(1)}上下各取若干个增量ΔZ2,形成新的廊道,再用动态规划法在该廊道内寻优,直至优化调度线全部为非廊道边界点和最大(小)库水位点所组成为止[8-9]。
3.2单库动态规划计算过程

(6)
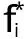
利用式(6)进行水库调度需对状态变量进行离散化。对调度期内,假设库水位在正常蓄水位和死水位之间连续变化,则可将水位划分为m-1个网格,共m个点,步长为ΔZ,如图1所示。
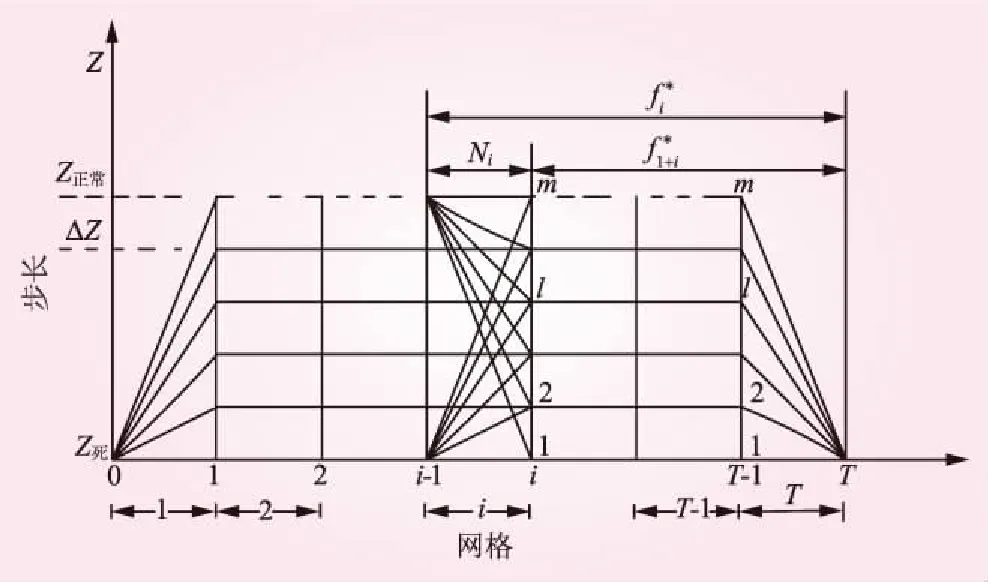
图1 动态规划网格
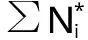
运用动态规划法计算:已知日调节水库的死水位、正常蓄水位、水位-库容关系、出库流量-尾水位关系、初始水位Z0,以及预报的各时段入库流量Qi,其求解计算流程如图2所示。
初选步长ΔZ1=0.1m,依据上述动态规划法计算流程求得初始优化调度线(水位精度为0.1m);而后选取若干个增量ΔZ2=0.01m,再用上述动态规划法在廊道内选优。由于ΔZ2=0.01m,优化计算的各时段库水位离理论最优过程不超过0.01m,而目前五凌电力水情测报的水位精度为0.01m,故求得的优化过程为目前测报精度下的最优过程。
采用VB6.0编程工具,开发实时优化调度系统。依托五凌电力办公网络环境,读取五凌电力梯级水库调度自动化系统oracle数据库中日96点发电计划、实时库水位、尾水位等相关数据,存入本地数据库,从而进行实时优化计算。
4参数及原始数据选取
系统优化计算所需参数主要包括来流量、限制出力及水位、水头-耗水率关系、水头-单机限制出力关系、水位-库容关系、出库流量-尾水位关系等。其中,水头-耗水率、出库流量-尾水位采用最新的水库实际运行数据进行拟合,图3、4分别为凌津滩水电厂水头-耗水率和出库流量-尾水位的拟合关系;机组检修、限制出力、限制水位等约束均根据运行中实际要求进行修改;期初库水位、尾水位从五凌电力梯级水库调度自动化系统oracle数据库中实时读取,期末库水位推荐为能蓄至的最高水位(上限为正常蓄水位)。
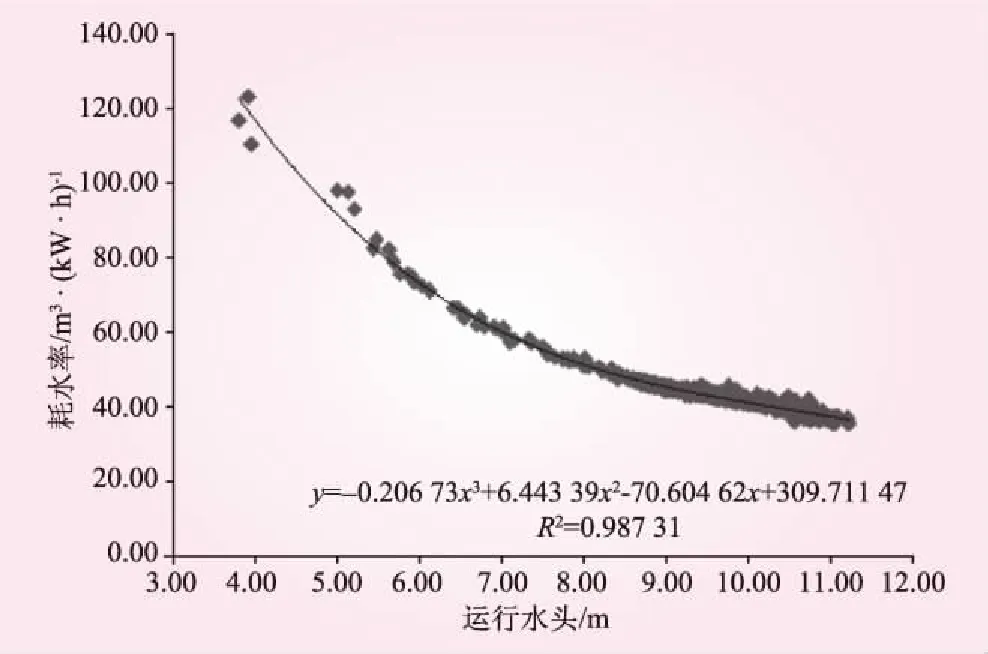
图3 凌津滩水电厂水头-耗水率关系拟合
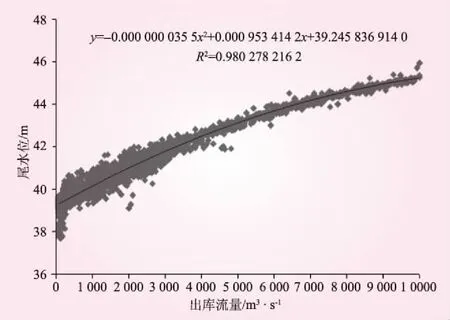
图4 凌津滩水电厂出库流量-尾水位关系拟合
对于模型优化计算,需准确可靠的入库流量过程。根据电网下达的上游水电厂日96点计划(从五凌电力梯级水库调度自动化系统oracle数据库中实时自动获取),采用上游电厂“水头-耗水率曲线”计算出发电流量过程,若上游电厂有弃水,读取弃水流量,再加上区间流量,即得到24h小时的实时入库流量过程[10]。
5实例计算及分析
5.1系统评价分析
选用6座径流式水电厂2012年~2014年实际水情资料,各水电厂按预期控制水位运行,可算得各电厂预期增加效益(见表2),与实际运行相比,平均每年可增加发电量4 500万kW·h。
表2径流式水电厂预期年增加效益分析
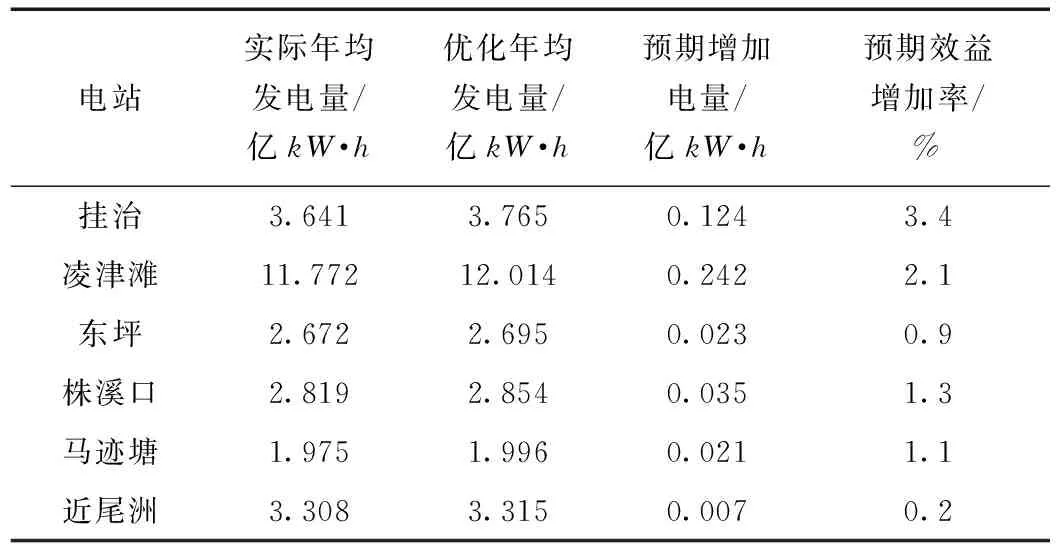
电站实际年均发电量/亿kW·h优化年均发电量/亿kW·h预期增加电量/亿kW·h预期效益增加率/%挂治3.6413.7650.1243.4凌津滩11.77212.0140.2422.1东坪2.6722.6950.0230.9株溪口2.8192.8540.0351.3马迹塘1.9751.9960.0211.1近尾洲3.3083.3150.0070.2
为进一步对比说明,选取2015年9月28日凌津滩水电厂实际运行情况与系统优化计算进行比较(期末水位相同):系统优化电量363.02万kW·h,实际发电量358.18万kW·h,增发电量4.84万kW·h,增发1.35%;优化调度系统计算的日均入库流量为1 784m3/s,而实际测报计算的日均入库流量为1 774m3/s,仅相差0.56%(准确率达99.44%)。图5为系统优化计算结果及过程与实际运行对比。
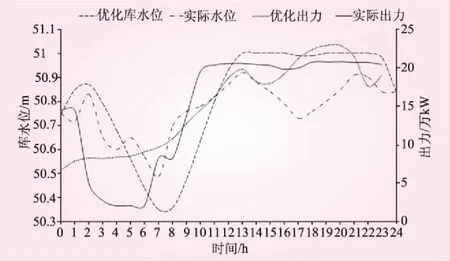
图5 2015年9月28日凌津滩水电厂系统优化结果与实际运行过程比较
由图5可知,在来流量增加前的入库流量较小阶段(3∶00~5∶00),应适当维持一定出力,一方面可在水头较高情况下适当发电;另一方面,可以适当“腾库”,在流量增加阶段出力不必增加过快,避免明显的抬高尾水位而降低发电水头。在来流量持续增加阶段(6∶00~10∶00),应根据入库流量情况适当加大出力,由于之前的“腾库”,所以该阶段不必过大、过快加大出力,以便维持较高运行水头;否则,该阶段出力快速、大幅增加,抬高了尾水位,从而明显降低了运行水头,使得该部分较大出力时段的耗水率偏大,整体发电效益达不到最优。在来流量较大且处于稳定阶段(18∶00~20∶00),尽量高水位运行,合理安排出力维持出入库平衡。在来流量减小阶段(20∶00~24∶00),应根据入库情况适当逐步降低出力以维持高水位。
所以,水库运行不能只关注高水位运行,应根据来水情况优化出力安排,降低整体耗水率,提高发电效益。通过该系统,可快速计算得出各种入库流量变化情况下整体发电效益最大的各时段出力安排与运行库水位。
5.2实时优化调度及分析
径流式水电厂实时优化调度系统以目前时刻为起点,进行未来24h的实时优化计算,得出可视化的水库最优运行过程,指导水库实时运行。以凌津滩水电厂为例进行计算说明。
现以当前时刻(11月17日08∶15)凌津滩水电厂进行实时优化调度计算:点击“凌津滩水电厂实时优化调度系统”,显示各计算参数,如五强溪日平均入库流量、五凌区间流量、期末推荐库水位、限制最高、最低库水位等,各参数均可根据实际发生的情况进行修改;然后点击“读取参数”,各时段入库流量、检修台数等亦可进行修改;最后点击“开始”按钮进行优化计算,得到优化计算结果界面如图6所示。由于设置了“时间间隔”,故系统可在设定的时间间隔,自动重新以当前时刻的参数、条件进行未来24h的优化计算,从而实现实时滚动的优化计算。

图6 2015年11月17日08∶15凌津滩水电厂实时优化调度计算结果
图6中计算结果显示了库水位、出力、入库流量、出库流量、水头等水库运行关键过程,以及可发电量、实发电量、蓄能电量、耗水率等优化计算值,其中:实发电量为由当前时刻到期末推荐水位的调度期内优化计算发电量,蓄能电量为期末、期初库容之差的水量按当日平均发电耗水率计算的发电量,可发电量为实发电量与蓄能电量之和。
同时,水库在运行过程中,若需指定时段的库水位,则可在“读取参数”步骤中,选择所需的计算时段和设置其控制水位,然后开始计算便可得到该时间内的最优过程。即该系统可根据运行需要,选择24h内任意结束的计算时段、满足库水位、机组运行台数等需要的最优运行过程。
因为本系统采用离散动态规划法逐步逼近寻优求解步长为0.01m,优化计算结果能达到目前水情测报精度(0.01m)下的最优过程,且经计算比较,与使用常规动态规划法直接求解的结果相同;同时,当计算时段长选为1h时,本系统计算时间只需0.250s(图6),而使用动态规划直接计算则需2.520s,若计算时段长选为30min或15min时,使用动态规划法直接计算耗时会更长。所以本系统节省计算时间显著且能达到最优值。
6结语
开发的径流式水电厂实时优化调度系统,可根据上游电厂发电计划和水库运行情况以及区间来水情况,较为准确计算入库流量过程,结合实际运行的条件和要求设定各参数值,能快速计算出最优的水库运行过程,并能按设定的时间间隔实时滚动向前更新计算,能很好地实时量化指导水电厂的负荷安排及申请,从而获得较好的经济效益,使水库优化调度理论较好地应用于实际生产运行。
参考文献:
[1]邓坤, 张璇, 杨永生, 等. 流域水资源调度研究综述[J]. 水利经济, 2011, 29(6): 23- 27.
[2]唐明, 马光文, 陶春华, 等. 水电站短期优化调度模型的探讨[J]. 水力发电, 2007, 35(5): 88- 90.
[3]王兴菊, 赵然杭. 水库多目标优化调度理论及其应用研究[J]. 水利学报, 2003(3): 104- 109.
[4]费如君, 卢毓伟, 樊绍华, 等. 梯级水电站短期优化调度算法研究及软件开发[J]. 水力发电, 2013, 39(7): 86- 88.
[5]黄益芬. 水电站水库优化调度研究[J]. 水力发电, 2002(5): 64- 66.
[6]倪建军, 徐立中, 李臣明, 等. 水库调度决策研究综述[J]. 水利水电科技进展, 2004, 24(6): 63- 66.
[7]畅建霞, 黄强, 王义民. 水电站水库优化调度几种方法的探讨[J]. 水电能源科学, 2000, 18(3): 19- 22.
[8]邹进, 刘可真. 水资源系统运行与优化调度[M]. 北京: 冶金工业出版社, 2006.
[9]杨侃. 水库优化调度中增量动态规划收敛性研究[J]. 水科学进展, 1995, 6(S1): 23- 29.
[10]李益民, 段佳美. 水库调度[M]. 2014年版. 北京: 中国电力出版社, 2014.
(责任编辑高瑜)
收稿日期:2015- 11- 19
作者简介:肖杨(1986—),男,河南固始人,助理工程师,硕士,主要从事流域水资源优化调度工作.
中图分类号:TV697.1
文献标识码:A
文章编号:0559- 9342(2016)04- 0097- 04
DevelopmentofReal-timeOptimizationDispatchingSystemforRun-offHydropowerStation
XIAOYang,KUANGLuzhang
(WulingPowerCorporation,Changsha410004,Hunan,China)
Abstract:In order to meet the requirements of hydropower station real-time scheduling, the real-time optimal scheduling model of run-off hydropower station is built with the goal of maximizing power generation. The discrete dynamic programming method is adopted in model calculation. The real-time optimal scheduling system can forecast the flow process of next 24 hours, and calculate the power generation process of next 24 hours which satisfies the requirements of constraint conditions in the ways of real-time and rolling. The system has been used in six run-off hydropower stations, and the results show that the accuracy rate of inflow calculation is more than 98% and the average annual power generation increases 45 million kW·h.
Key Words:run-off hydropower station; real-time optimization dispatching; discrete dynamic programming

