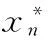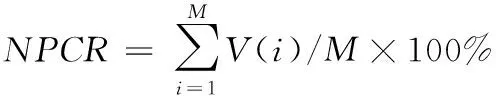基于通信编码序列与多混沌图像加密算法

杨晓刚　刘国荣　毛彦斌

(西安交通大学电子信息工程学院　陕西 西安 710049)



基于通信编码序列与多混沌图像加密算法

杨晓刚刘国荣毛彦斌

(西安交通大学电子信息工程学院陕西 西安 710049)

摘要结合量子混沌映射的良好特点，首次提出一种全新的基于通信编码序列与多混沌映射的图像加密算法。该算法运用量子Logistic和Logistic两种不同的混沌映射，结合通信领域常用的无线编码技术，灵活地运用模板图像对原始图像像素进行编码加密。实验表明，该算法既可以很好地拓展密钥空间，又可以成功地抵御统计分析等各种攻击操作，具有很强的前瞻性和创新性。

关键词通信编码模板图像量子混沌图像加密

0引言

随着DNA计算的发展和运用，基于DNA序列的图像加密算法也越来越多地出现于各类期刊文章中。同时，随着无线电编码技术的日益成熟，莫尔斯电码编码规则也渐渐地淡出了人们的视野。但利用莫尔斯电码符号传递数据这一通信方式今天依然被广泛使用，特别是在无线电通信领域。为增强图像加密算法的安全性和高效性，首次提出一种基于通信编码规则的多混沌图像加密算法。在主动克服了低维单混沌序列弱点的同时，充分发挥通信编码的特殊性和量子混沌映射优势，有效地解决了低维混沌系统缺陷的问题，也进一步丰富了加密的手段和样式。

1通信编码序列

1.1莫尔斯密码

从事通信领域研究的人员，普遍对莫尔斯电码有所了解。文中所讲到的通信编码即指莫尔斯编码。莫尔斯编码是对莫尔斯电码符号进行编码后所得的结果。莫尔斯电码是利用电流的闭合、断开来产生划、点符号，即“-”和“.”，在语言上读作“嗒”和“嘀”，之后根据点、划的特定组合，将字母、数字及各类语言符号进行特殊编码，产生了一种特殊的编码规则。而后，成功地将该编码规则应用到无线电通信领域，产生了长码和短码两种不同编码规则的莫尔斯密码。文中所谈到的，均是针对短码而言。早期，莫尔斯密码是运用莫尔斯编码规则所进行的编码结果。对数字的编码规则原型如表1所示。

表1　莫尔斯密码的原型

而经过长期的实践运用，目前对于数字的编码规则已有所变化，如表2所示。

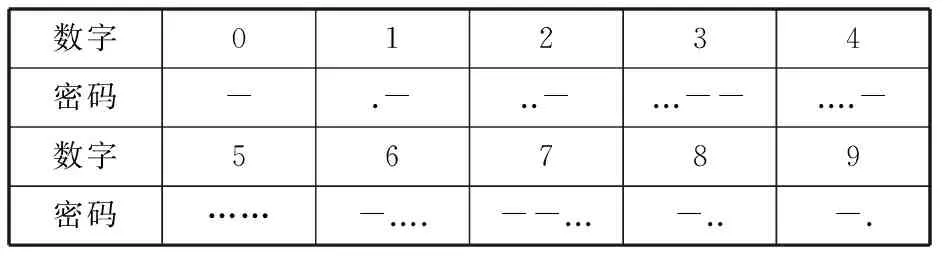
表2　莫尔斯密码的新品种

1.2密码序列

将“.”定义为“0”，类似于电路中的低电平；“-”定义为“1”，类似于电路中的高电平。同样，也可作相反定义。这样，对数字的莫尔期密码如表3所示。

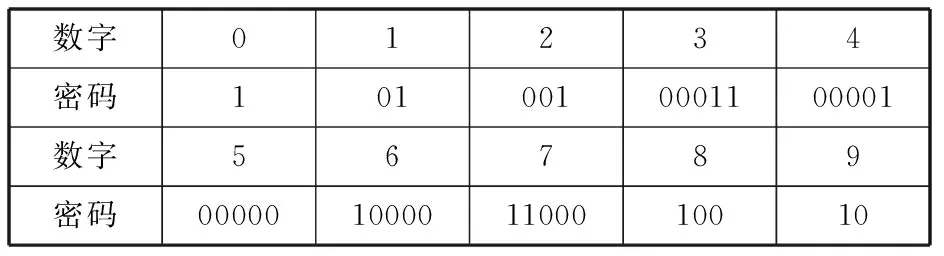
表3　莫尔斯密码的01编码

对于任何一个数字，均可用如上编码规则给予编码，如234，即为0010001100001。为了进一步提高编码规则的安全性，对如上映射关系又作了进一步的变化，即数字与密码之间的映射关系不是固定不变的，而是根据外部条件的变化而适时变化。同时，01编码之间也存在着许多运算规律，如互逆、取补、移位等，而且编码后所得结果的位数也不相同，这在一定程度增加了算法的多样性和安全性。

1.3混沌映射

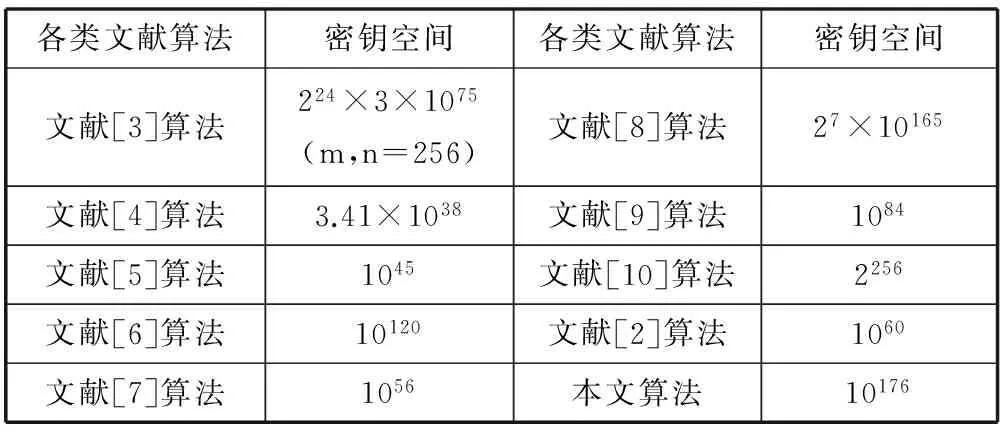
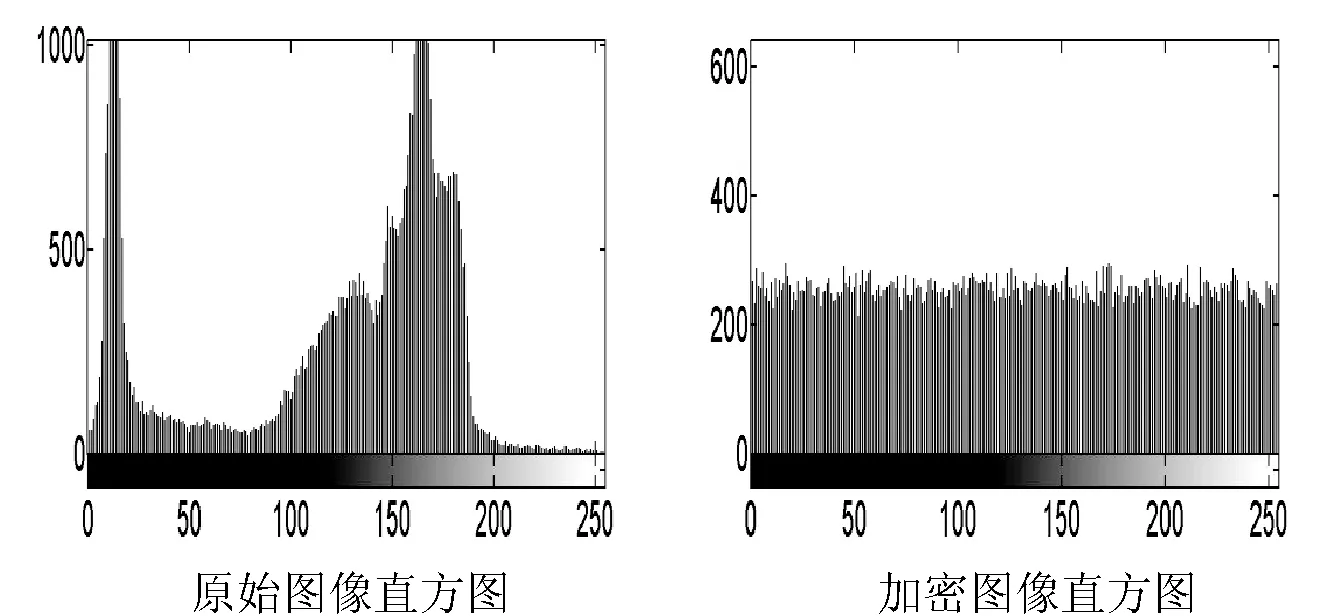
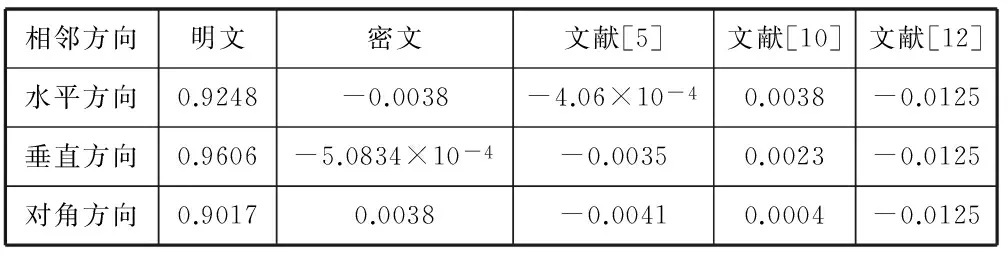
Logistic映射是一个常见的低维混沌系统，其中，初值和参数的设置为3.569945

wn+1=twn(1-wn)

(1)

根据式(1)得到的混沌序列wn在[0,1]之间无规律地震荡变化。

量子Logistic映射是一种具有良好密码性能的多维混沌映射，其具有经典混沌系统的自然属性,其定义如下：

(2)

1.4加密方案

文中提出的加密算法具体步骤如下：

1) 根据输入密钥，运用Logistic映射生成一维混沌序列A。其中A={A(i),i=1,2,…,S}，S为原始图像像素点的总数。

2) 对A序列元素指定倍数(10p，p为正整数，文中取p=3)放大并取整后，再进行求模运算，将所得的结果A*转换为模板图像矩阵(m×n)。其中，m、n为原始图像数据矩阵的行数和列数。

3) 再次运用Logistic映射，在新的密钥及迭代次数N的情况下，生成x(N)。

4) 建立数字0～9与莫尔斯密码之间的所有映射关系，根据关系总数(10!)将0～1等分为若干份，然后由第3步所得结果选择编码规则区间，生成新的01编码规则。

5) 根据第4步的结果对第2步中的矩阵元素进行逐位01编码，生成长度不一的01串矩阵。

6) 根据矩阵中每个元素序列中1的个数来决定是否对该序列执行取反操作。本文中，若元素序列中1的个数为偶数或0，则取反，否则不变。

7) 对第6步的结果进行十进制转换，并再次进行求模运算，得到不同于第2步的新的模板图像矩阵，其矩阵的行数和列数亦为m、n。

8) 根据第一轮量子Logistic映射的初始值a、b、x0、y0和z0及迭代次数N1，生成3个混沌序列。取某一时刻i的混沌值与调制因子r相乘，生成新一轮量子Logistic映射的初始值x1、y1和z1，即x1=x(i)×r，y1=y(i)×r和z1=z(i)×r。新一轮量子映射的可调参数和耗散参数作为密钥不同于a、b。

9) 运用第二轮量子Logistic映射产生长度为m×n的混沌序列和xn,yn并对两个序列按升序进行排列，根据排列编号即索引分别对原图像矩阵及第7步所得模板矩阵进行全局置乱，生成长度为m×n的置乱序列J和D。

10) 对原始图像生成的置乱序列值进行第1轮加密。首先对第1个像素点采用如下方式进行加密：

F(1)=[J(1)⊕D(1)+D(1)]mod256

(3)

对置乱序列其他位置像素点按照如下公式进行加密：

F(i)={[J(i)⊕D(i)+D(i-1)]mod256}⊕F(i-1)

(4)

11) 对第1轮加密的结果接着进行第2轮加密，其中，第1个像素点采用如下方式加密：

E(1)={[F(1)⊕D(1)+D(1)]mod256}⊕F(m×n)

(5)

其他位置像素点按照如下公式进行加密：

E(i)={[F(i)⊕D(i)+D(i-1)]mod256}⊕E(i-1)

(6)

将加密后的序列E转化为二维矩阵，得到最后的加密图像。解密过程是加密过程的逆操作。在此，不再作详细说明。

2仿真实验与分析

本文运用Matlab 2012软件，分别对尺寸大小均为256×256的Rice、Lena和Cameraman灰度图像。采用2个Logistic映射和2个量子Logistic映射的图像加密算法对原始图像进行加密操作。第一个Logistic映射的初始值t=3.65411、w1=0.48651；第二个Logistic映射的初始值t=3.8427、w1=0.33265、迭代次数N=10 000。第一个量子Logistic映射的初始值a=3.9、b=4.5、x0=0.32、y0=0.12565、z0=0.1234和迭代次数N1=5 000；第二个量子Logistic映射的初始值a=3.98、b=6.22、i=4899、r=0.3。

2.1密钥空间分析

如表4所示，对于图像加密算法来说，密钥空间的大小是度量一个算法好坏的重要技术指标。在本文中，算法的迭代次数N、N1及时刻点均是正整数，且1≤i≤N1，两个Logistic映射的w1、t及量子Logistic映射的初始值x0、y0、z0，参数a、b、r的值都为小数。假设计算机精度为10-16，则密钥空间为1016×1016×1016×10128=10176。与文献[3-9]中的加密算法密钥空间相比较，加密空间提高了多倍。与文献[2]加密空间相比较，也提高了很多，在抵御穷举法攻击方面具有良好的空间特性。

表4　各类文献算法的密钥空间比较

2.2统计特性分析

对于图像处理过程来说，加密结果与原始图像之间的相关性越小，说明该算法抵御统计攻击的能力越强。这种相关性不仅体现在像素点位置的置乱上，也体现在像素值的替换上。目前，定量地分析这种相关性的方法有直方图分析、信息熵分析、相邻像素间的相关性分析、明密文图像相关性分析、图像的幅值频谱图分析等。下面结合仿真实验逐一进行分析，并与相关文献结果作同类对比。

2.2.1直方图

图1分别给出了明文Rice、Lena、Cameraman图像及其对应的密文图像像素分布规律直方图。从图中可以看出，原始图像的直方图在整个空间呈高低起伏状态，甚至部分图像的像素值分布过于集中，主要集中在某一区间内。而加密后的图像，直方图比较均匀，峰值与均值差异较小，说明加密后的图像在灰度值值域内近似等概率取值，具有很好的随机特性，也说明了加密后各像素之间的相关性得到了很好的削弱。因此，该算法具有很强的抵御统计攻击分析的能力。

图1　3种测试图像原始图像、加密图像、解密图像及其直方图

2.2.2信息熵

由信息熵的定义可知，信源的信息熵计算公式如下：

(7)

式中，p(mi)为信号mi出现的概率，L为每个信号的比特数。从理论层面上来讲，理想情况下密文图像的信息熵应该为8(主要针对8位二进制的灰度图像来说)。经实验测试，运用本文算法对图像Rice、Lena和Cameraman的加密图像其信息熵分别为：7.9972、7.9964、7.9972，这些值与理想值非常接近。反映出该算法在加密的过程中对原始图像的信息做了很好的隐藏，在抵御熵攻击方面具有良好的抗攻击特性。

2.2.3相邻像素点的相关性

实验做法是：分别从原始图像和加密后的图像中选择水平方向相邻的像素对、垂直方向相邻的像素对及对角线方向相邻的像素对各1000对，定量地计算其相邻像素之间的相关系数。经过实验，结果如表5所示。与文献[5,10,12]相比，运用文中所提算法加密后的图像在三个方向上相邻像素点的相关性系数都比较小，相邻的两个像素之间基本不相关。这说明明文图像经加密过后，其原有的图像信息统计特性已被很好地扩散到随机的密文图像中，具有了更高的安全性。

表5　明文和密文Lena图像相邻像素的相关系数

2.2.4明密文图像相似度

直方图仅从视觉上反映像素值的分布特性，但是对于这些像素原来的位置在直方图中并没有体现，对于图像内部到底存在什么样的物体，形状是什么，每一块的灰度分布是什么样的这些信息在直方图中均被省略掉了。针对此方面的问题，有人提出了利用二维相关系数[13]来分析明文图像和密文图像之间的相关性。本文提出了用图像相似度来度量两幅图像之间的匹配程度。图像相似度计算主要用于对于两幅图像之间内容的相似程度进行打分，根据分数的高低来判断图像内容的相近程度。若加密后的图像与原图像有许多相似的地方，那么加密图像的安全度就比较低。设G=(gij)M×N,C=(cij)M×N是明文和密文图像，α、β是两个整数，且0≤α

(8)

其中，XSD表示两幅图像的相似度。XSD介于0和1之间，其值越小，说明加密算法的安全性越高。当α=β=0时，反映的是明文图像与密文图像对应点的灰度变化情况，依据灰度变化情况来度量加密前后图像的相似程度；对于图像的分块平移操作，该取值却不能准确反映明文图像和密文图像之间的相似情况。当α、β取不同值时，不仅能反映两幅图像的相似程度，也能反映图像的平移性。因此，对于一个算法来说，需要选择合适的参数α、β值。

XSD(Rice.bmp,Ricem.bmp)=0.0992

XSD(Lena.bmp,Lenam.bmp)=0.4858

XSD(Cameraman.bmp,Cameramanm.bmp)=0.4803

通过实验可以看出，明文图像和密文图像之间的相似度很低，特别是针对Rice图像来说，明文图像与密文图像之间几乎毫不相关。

2.2.5图像的幅值频谱图

图像可以看作是一个定义在空间域的二维平面上的信号，该信号的幅值对应于像素的灰度值。图像的频率又称为空间频率，它反映了图像中各像素灰度值在空间中的变化情况，而幅值频谱图则用来反映图像频率统计分布情况。文中，我们经二维傅里叶变换来定量地反映图像的空间频率能量的分布情况。通常情况下，我们习惯将图像频率的低频成分放在幅度谱的中央，而将高频成分放在幅度谱边缘。而对于一幅原始图像来说，其幅值频谱图符合上述规律，即其在二维空间显示上过于集中，在三维空间上，它的频谱分布会出现一个凸起的部分。而经过加密处理之后，无论是在二维空间，还是在三维空间，均会呈现出均匀、平整的状态，即幅值会被均匀地扩散到整个二维或三维空间中，从而使得原始图像的频率特性被充分地扩散开来。实验结果正好印证了这一点。同时，在正确解密之后，可以看出，明文图像的幅值频谱图与解密后的图像幅值频谱图相同，这说明加密算法的灵敏度很高，匹配度很高。二维和三维幅值频谱图的一致相关性，在很大程度上反映了该算法在防止密文信息泄露方面具有相当的安全性。

采用文中算法对标准256×256 Lena图像进行加密和解密，其二维和三维的幅值频谱图如图2所示。其中，(a)、(b)、(c)分别是原始图像、加密图像及解密图像的二维幅值频谱图，(d)、(e)分别是原始图像和加密图像的三维幅值频谱图。解密图像的三维幅值频谱图与原始图像的完全一致。

图2　Lena图像的二维、三维幅值频谱图

2.3对明文敏感性的分析

NPCR值是用来定量地衡量密文对明文敏感性的惯用指标，其主要是通过对密钥或原始图像中像素点灰度值的微小改变来检测加密结果的变化剧烈程度，即变化率。变化率可通过以下公式求得：

(9)

(10)

其中，P(i)和P*(i)分别是改变前与改变后两种加密结果对应于同一像素i的灰度值。一般来说，一个标准的8位的灰度图像，其NPCR值为99.6094%[2]。实验结果如表6所示，对于不同的测试图像，NPCR值均与理想值很接近，说明该算法对明文图像具有很强的敏感性，可有效抵制已知明文攻击与选择明文攻击，具有一定的抵御差分攻击的能力。

表6　常见测试图像的NPCR值

3结语

本文首次提出了基于通信编码与多混沌系统的图像加密算法，类似于当初的基于DNA序列的图像加密算法。虽因编码规则的多样性及运算的复杂性，在运算效率上还有一定差距，但基于该领域的加密算法研究数量很少。算法对明文和密钥均具有很强的敏感性，同时具有良好的统计特性，密钥空间大，安全性高。经仿真实验测试，该算法能很好地抵御各类攻击操作，确保图像加密、传输的安全。同时，因与无线电密码技术相结合，对密钥的传输也可改变传统意义上网络传输等模式，改用无线电编码传输，进一步增加了传输样式的多样性和安全性。

参考文献

[1] Goggin M E,Sundaram B,Milonni P W.Quantum logistic map[J].Physical Review A,1990,41(10):5705-5708.

[2] 朱从旭,黄大足,郭迎.结合多混沌映射和输出反馈的图像加密算法[J].武汉大学学报:信息科学版,2010,35(5):528-531.

[3] 罗玉岭,杜明辉.基于量子Logistic映射的小波域图像加密算法[J].华南理工大学学报:自然科学版,2013,41(6):53-62.

[4] Chen Guanrong,Mao Yaobin,Chui Charkes K.A symmetric image encryption scheme based on 3 D chaotic cat maps[J].Chaos Solutions & Fractals,2004,21(3):749-761.

[5] 朱从旭,陈志刚,欧阳文卫.一种基于广义Chen’s混沌系统的图像加密新算法[J].中南大学学报:自然科学版,2006,37(6):1142-1148.

[6] 陈艳峰,李义方.交替分段相互置乱的双混沌序列图像加密算法[J].华南理工大学学报:自然科学版,2010,38(5):27-33.

[7] Zhu Congxu.A novel image encryption scheme based on improved hyperchaotic sequences[J].Optics Communications,2012,285(1):29-37.

[8] 文昌辞,王沁,黄付敏,等.JPEG彩色图像白适应加密算法[J].计算机辅助设计与图形学学报,2012,24(4):500-505.

[9] Bhatnagar G,Wu Q M Jonathan.Chaos.based security solution for fingerprint data during communication and transmission[J].IEEE Transactions on Instrumentation and Measurement,2012,61(4):876-887.

[10] Akhshani A,Akhavan A,Lim S C,et al.An image encryption scheme based on quantum logistic map[J].Communications in Nonlinear Seience and Numerical Simulation,2012,17(12):4653-4661.

[11] Behnia S,Akhshani A,Mahmodi H,et al.A Novel Algorithm for Image Encryption Based on Mixture of Chaotic Maps[J].Chaos,Solutions & Fractals,2008,35(2):408-419.

[12] Wang X,Zhao J,Zhang Z.A Chaotic Cryptosystem Based on Multi-one-dimensional Maps[J].Modern Physics Letters B,2009,23(2):183-189.

[13] Chen G,Mao Y,Charles K.A Symmetric Image Encryption Scheme Based on 3D Chaotic Cat Maps[J].Chaos,Solitons and Fractals,2004,21(3):749-761.

[14] 詹新生.图像加密置乱性能分析[D].郑州:郑州大学,2005.

收稿日期：2015-01-08。陕西省自然科学基金项目(2014JM83 22)。杨晓刚，硕士生，主研领域：图像处理。刘国荣，副教授。毛彦斌，硕士生。

中图分类号TP309

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.068

MULTI-CHAOS IMAGE ENCRYPTION ALGORITHM BASED ON COMMUNICATION CODING SEQUENCE

Yang XiaogangLiu GuorongMao Yanbin

(SchoolofElectronicsandInformationEngineering,Xi’anJiaotongUniversity,Xi’an710049,Shaanxi,China)

AbstractCombining the good characteristic of quantum chaos mapping, this paper puts forward for the first time a brand new image encryption algorithm which is based on communication coding sequence and multi-chaos mapping. The algorithm uses two different chaotic maps (quantum Logistic and Logistic), in combination with wireless coding technology commonly used in communication field, it flexibly uses the template image to encode and encrypt original image pixels. Experiments show that the proposed image encryption algorithm can well expand the key space, and meanwhile successfully resists various attacks such as statistical analysis operation, thus has strong forward-looking and innovative properties.

KeywordsCommunication codingTemplate imageQuantum chaosImage encryption