CZ法硅单晶生长电阻网络建模及MPC仿真分析

弋英民， 张　潼

(西安理工大学 自动化与信息工程学院, 陕西 西安 710048)



CZ法硅单晶生长电阻网络建模及MPC仿真分析

弋英民， 张潼

(西安理工大学 自动化与信息工程学院, 陕西 西安 710048)

CZ法硅单晶生长系统具有强非线性及大滞后的特点。本文就该系统建立了传热传质的低阶模型，计算了该模型在初始条件下的稳态解，并进行线性化处理及分析，根据系统的可控性及稳定性确定控制策略，并设计控制器。结果表明：在低阶模型中，采用Gevelber提出的简化辐射角系数能较好的反映工业中晶体生长过程特性；系统线性化后的性能分析表明，仅将加热器功率作为输入时，系统是不可控不稳定的，故采用模型预测控制算法作为控制策略，设计了无干扰无延迟的无约束模型预测控制器和无干扰有延迟的无约束模型预测控制器，仿真结果验证了所设计的方法的有效性。

单晶硅; CZ法; 电阻网络类比; 低阶模型; 模型预测控制

单晶硅半导体硅材料是电子信息技术产业以及新能源产业的基础材料，也是半导体器件和集成电路的重要原材料，因此在增大硅单晶直径的同时，提高直拉单晶硅的质量仍是研究的主要内容[1]。而CZ法是工业化生产单晶硅的最主要方法，其生长过程中既有物质的传输，也有动量和热量的传输[2]。坩埚内熔体的流动、传热及传质现象直接影响单晶硅的质量。国内外主要从理论分析、实验测定和数值模拟[3,4]三个方面对晶体生长过程进行研究[5]，Derby、Brown[6-7]、Hurle[8]等在晶体生长理论建模方面做出了大量贡献；Brice[9]、Jones[10]、Seidl[11]等通过实验研究分析了晶体生长过程中坩埚旋转和杂质氧等因素对硅单晶质量的影响。但是实验成本高、耗时长等原因制约了实验测定方面的进一步研究。

本文对CZ法生长单晶硅过程中的等径阶段采用电路类比法建立基于传热传质现象的低阶模型，并以此作为系统分析和控制算法研究的基础。

1　模　型

本文在热量、质量传递基本定律的基础上[12-15]，建立了具有两个输入量(Vp和Pin)、八个状态量(Th、Tc、Tm、Ri、Hi、Re、Hm和φ)和两个输出量(Tm和Ri)的低阶模型，根据加热器、坩埚、熔体的辐射传热和传导传热现象，采用电阻网络类比的方法建立单晶硅生长系统的温度状态方程；主要在熔体-晶体分界面处，根据分界面的几何形变建立几何状态方程。系统低阶模型是一系列具有如下形式的非线性方程：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

式中，Vp是提拉速率，Pin是加热器输入功率，Th是加热器温度，Tc是坩埚温度，Tm是熔体温度，Ri是分界面半径，Hi是分解面高度，Re是有效半径，Hm是熔体高度，φ是接触角。

2　建模的方法步骤

2.1建立晶体生长的温度状态方程

单晶炉内的热量传递方向及单晶炉部分尺寸如图1所示。温度状态方程涉及CZ法晶体生长系统中的大部分组分，即加热器、坩埚和熔体的温度。该状态方程以辐射传热和传导传热引起的能量平衡公式(9)为基础。

Ein-Eout=Estored

(9)

式中，Ein是系统接收的能量，Eout是系统耗散的能量，Estored是系统存储的能量。根据式(9)的系统能量平衡方程可以得到系统的温度状态方程。

对于加热器：

(10)

对于坩埚：

(11)

对于熔体：

(12)

式中，Ch是加热器热容，qhc是加热器传递至坩埚的传热速率；Cc是坩埚热容，qco是坩埚传递到周围环境的传热速率，qcs是坩埚传递到熔体表面的传热速率，qcm是坩埚传递到熔体内部的传热速率；Cm是熔体变化的热容，qso是熔体表面到周围环境的传热速率，qm是熔体到固液分界面区域底部的传热速率，Rcru是坩埚的半径；Hcru为坩埚的高度。

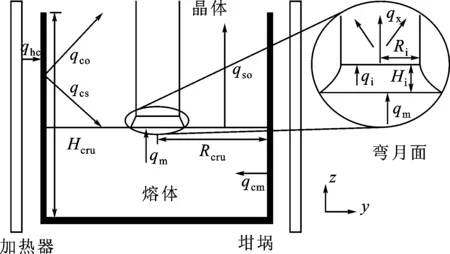
图1　传热率及系统尺寸Fig.1　Heat transfer rates and dimensions

2.1.1辐射角系数计算

单晶炉内主要涉及的辐射角系数有：坩埚到熔体表面的辐射角系数、坩埚到周围环境的辐射角系数、熔体表面到周围环境的辐射角系数。

1) 基本模型：图2为辐射角系数的角度近似。根据图2所示的坩埚内角度近似关系，可以得出辐射角系数的近似结果。图中，γ、ω分别为坩埚表面、熔体表面之间的夹角，H为暴露的坩埚壁高度。

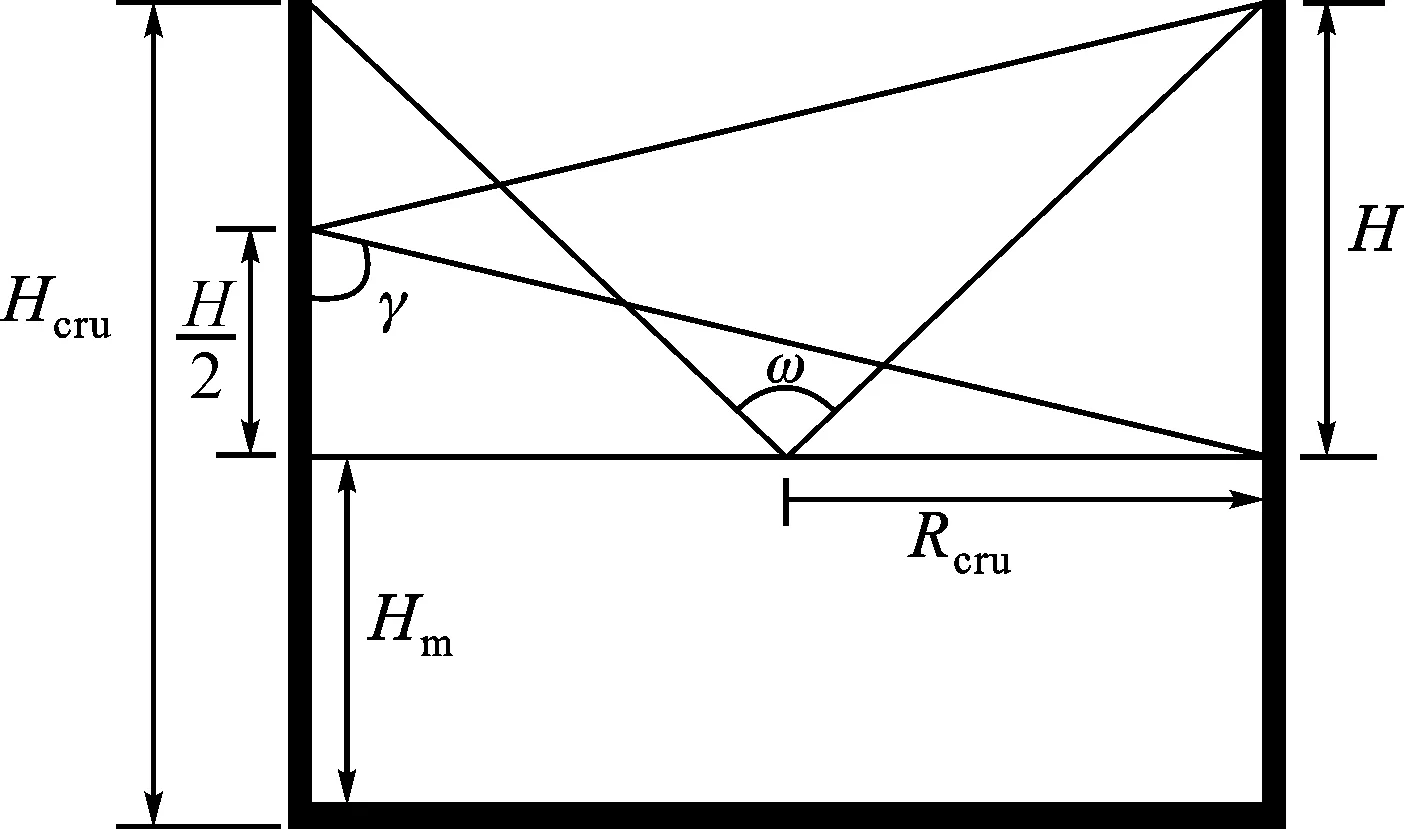
图2　辐射角系数的角度近似Fig.2　View factor angle approximation

2) 辐射增强模型：对两个表面A1和A2之间辐射角系数的定义式进行精确求解：

(13)

式中，R是两个表面之间的距离；θ1和θ2分别表示两个表面上的微小面积dA1、dA2间各自的天顶角。

2.1.2传热速率计算

将坩埚内熔体以上部分看作一个圆柱形外壳。下表面为熔体表面，即表面1；上表面为关于坩埚内部环境的假象表面，即表面2；侧表面为暴露坩埚壁的表面区域，即表面3。

1) 基本模型：认为在换热过程中一次仅有两个表面相互接触[8]，并进行热量传递。

采用电阻类比法对接触表面进行分析，即表面的传热速率qj、表面间的传热速率qjk类比为电流，辐射能量Ebj和能量Jj类似电压，辐射角系数和对应面积的相关项记为表面辐射热阻Rj和空间辐射热阻Rjk(j=1、2、3，k=1、2、3)。通过电路求解得出相关传热速率。

2) 辐射增强模型：认为换热过程中三个表面之间的传热同时进行，同样采用电阻类比法对接触表面进行分析，如图3所示。在节点1和节点3处根据基尔霍夫定律列出节点方程，计算求解相关传热速率。

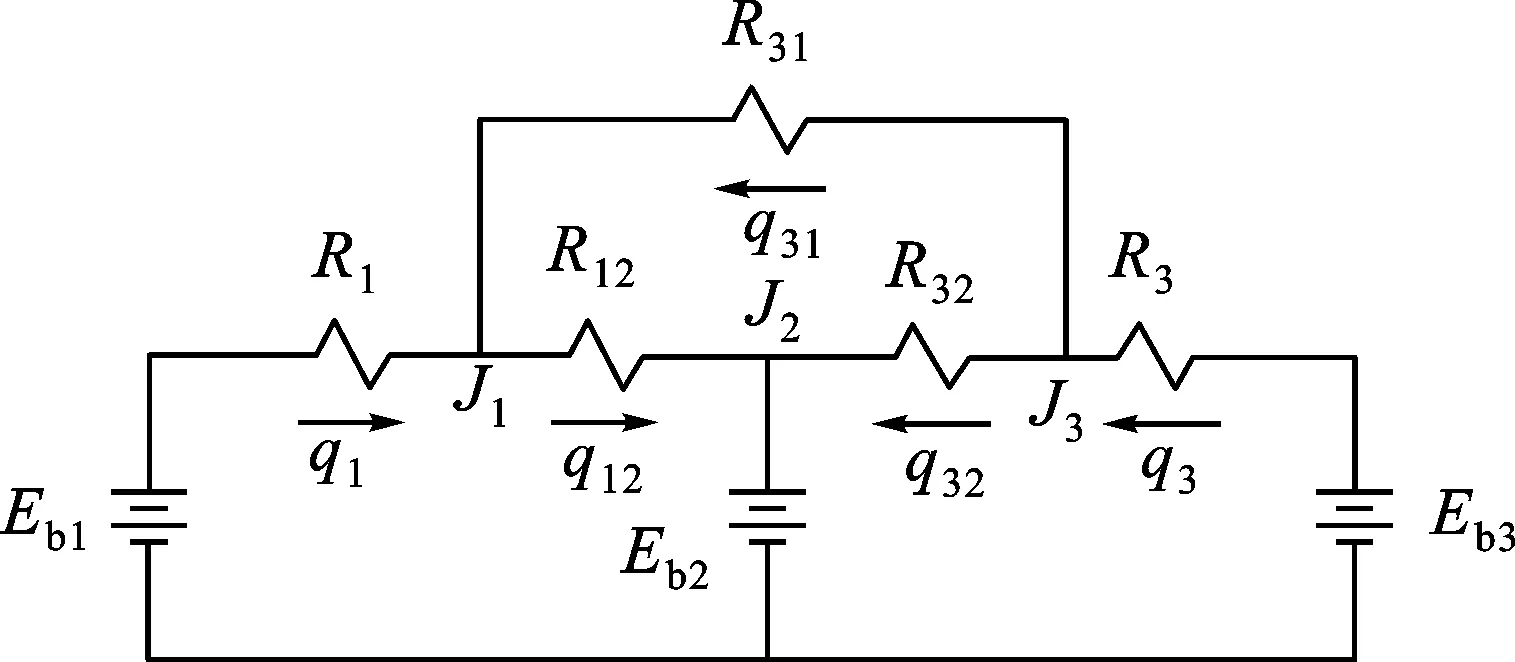
图3　圆柱体外壳电路类比Fig.3　Circuit analog of cylindrical enclosure

2.2建立固液分界面的几何状态方程

几何状态方程涉及CZ法晶体生长系统的几何形变，尤其是熔体-晶体分界面处的形变，即分界面半径、分界面高度、接触角、有效半径以及熔体高度。该状态方程以熔体-晶体分界面处的传热传质现象为基础。

熔体高度：

(14)

分界面高度：

(15)

分界面半径：

(16)

有效半径：

(17)

τ=fmRi/Vp

(18)

分界面高度和接触角：

(19)

(20)

(21)

Dφ=βRi(8Ri2cosφ+βcosφsinφ-sinφS1)

(22)

式中，ρs和ρl分别是硅固体和硅液体的密度，qx是晶体的传热速率，qi是从弯月板区域到固液分界面的传热速率，Hf是材料的融合比热，φ0是非零接触角，β是材料的拉普拉斯常数，fm是介于0.25～0.50间的比例参数。

3　模型验证及仿真实验

仿真中的状态参数如表1、表2所示[9]，在Matlab中对基本模型和辐射增强模型中的辐射角系数进行计算仿真，结果如图4所示。

表1　仿真中的常量值

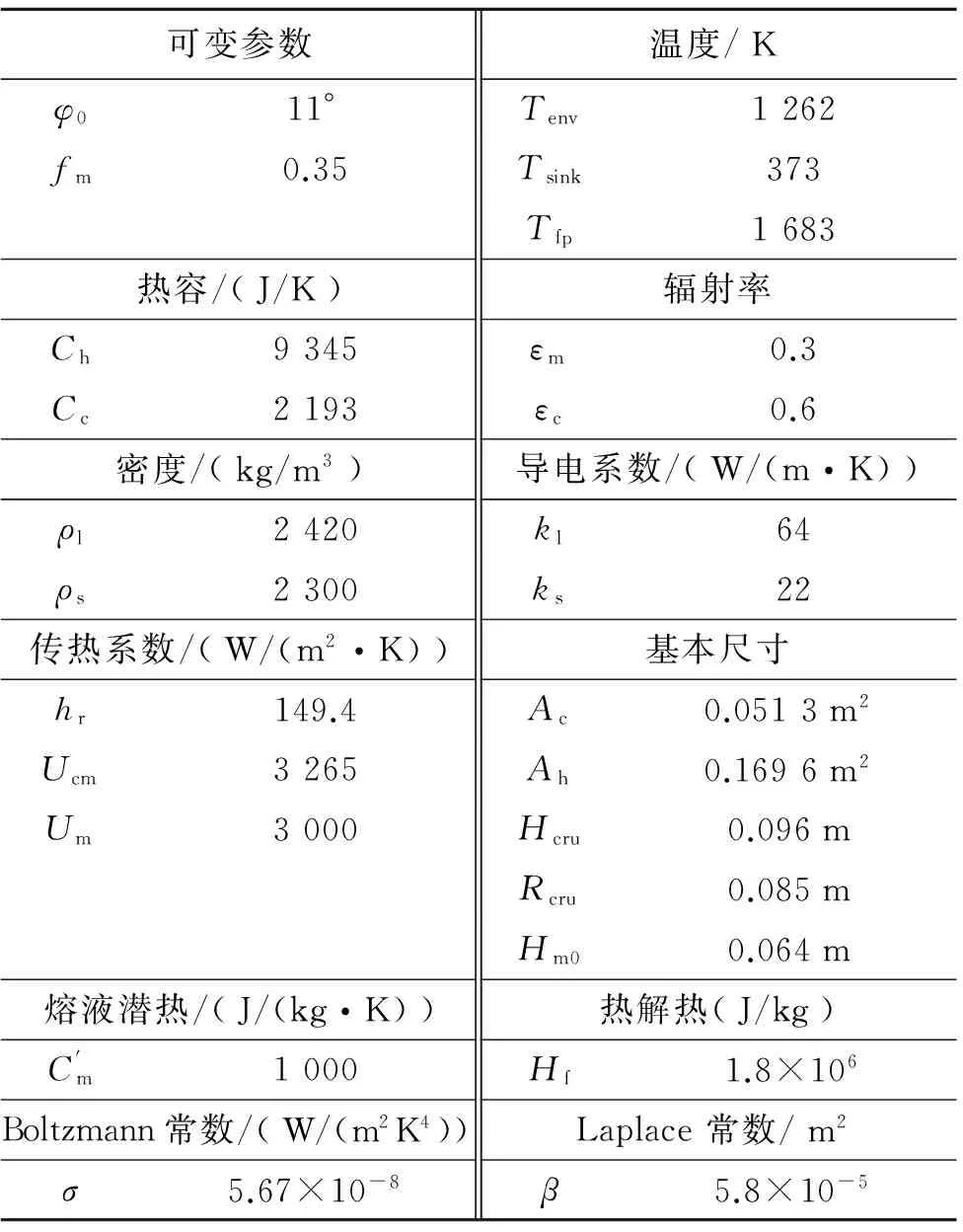
表2　硅晶体生长参数

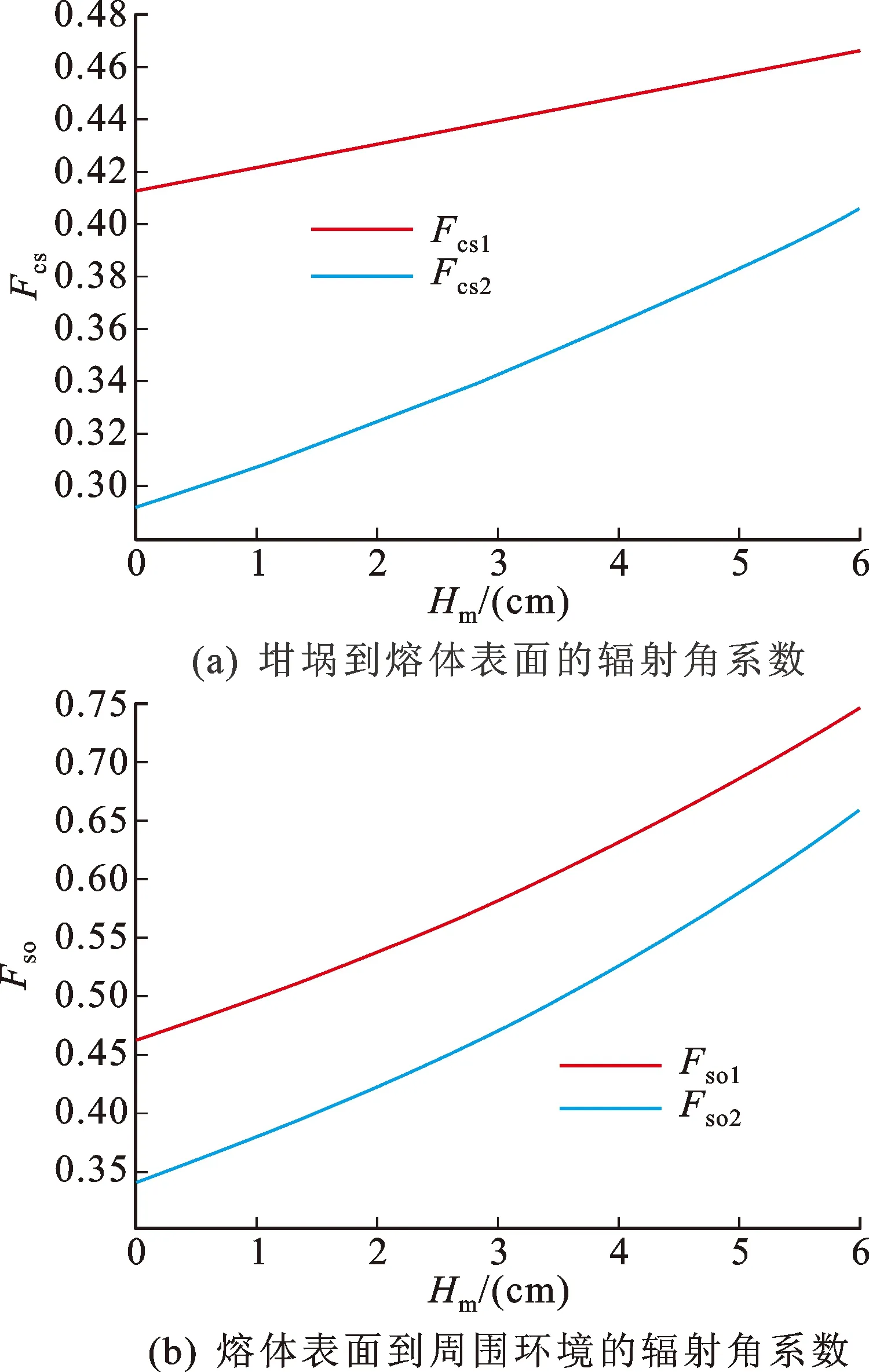
图4　基本模型和辐射增强模型中辐射角系数比较Fig.4　Radiation angle coefficients in basic model and radiation enhancement model

图4(a)说明了基本模型中坩埚到熔体表面的辐射角系数Fcs1和辐射增强模型中坩埚到熔体表面的辐射角系数Fcs2随熔体高度Hm的变化趋势；图4(b)则说明了基本模型中熔体表面到周围环境的辐射角系数Fso1和辐射增强模型中熔体表面到周围环境辐射角系数Fso2随熔体高度Hm的变化趋势。从图中可以看出，这两种类型的辐射角系数在数值上并不相同，但在趋势上是相同的，都是随着熔体高度的增加而递增。其中，Gevelber等人已验证了基本模型在CZ法晶体生长系统中应用的正确性[9]，因此这两种模型的辐射角系数的计算方法都能够用于CZ法晶体生长系统的研究。

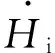
k1Tc4+k2Tc+k3=0

(23)

从而得到Tc的解轨迹表达式，k1、k2、k3为该方程的系数。同理，依次推导Th和Pin的解轨迹表达式。利用maple软件进行解轨迹的计算，结果如图5所示。

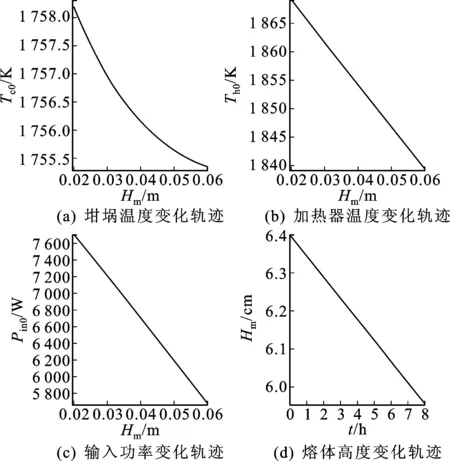
图5　初始条件下系统开环解轨迹Fig.5　Trajectory of open loop solution under initial conditions

在表1和表2所示的初始条件下(即：Ri=2cm，Tm=1 740K，Vp=2cm/h)，坩埚温度、加热器温度、输入功率随熔体高度Hm的变化轨迹如图5(a)、(b)、(c)所示，在图中分别用Tc0、Th0、Pin0代表初始条件下的变化轨迹。Hm随t的变化轨迹如图5(d)所示。由于在实际工业生产中，坩埚内熔体的高度是不断下降的，因此观察图5所示的温度变化轨迹时，应从坐标轴的横轴由右向左看，从图中可以看出，单晶炉内的主要组分的温度在晶体生长过程中的变化都是随着熔体高度的下降而逐渐升高的。此外，Hm随时间的增加而线性递减，其变化非常小，一小时约下降0.5 mm，因此可以认为在一定的时间范围内，熔体高度是不变的，这也就意味着，在一定程度上单晶炉内的温度是恒定的。

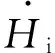
图7为坩埚温度随熔体高度的变化关系。从图中可以看出其趋势是相同的，仅在数值上有所不同，其中辐射增强模型的温度值更高一些。这一现象完全符合实际物理特性，由于辐射增强模型每次辐射换热时同时考虑到三个表面之间的相互作用，这与基本模型相比，捕获了更多的辐射换热损失。

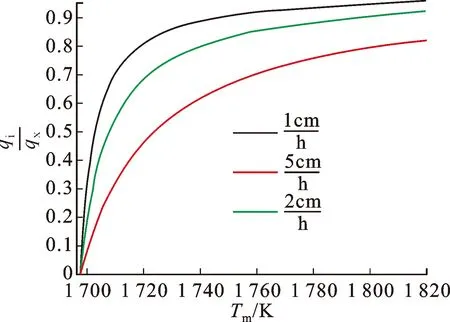
图6　熔体温度Tm和qi/qx的关系Fig.6　The relation between Tm and qi/qx

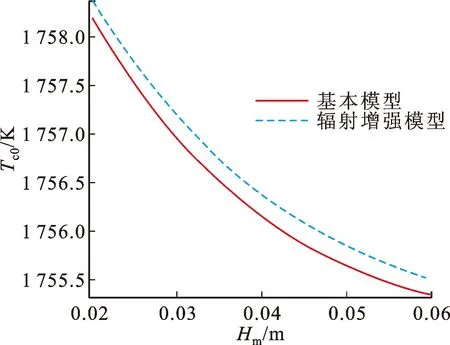
图7　坩埚温度随熔体高度的变化关系Fig.7　The relation between crucible temperature and melting height

4　系统分析

本研究所建立的系统方程是高度耦合的、非线性的以及时变的，这意味着对系统的分析会是在数学上的加强分析，而且控制器的设计会被复杂性所限制。因此，控制系统开发的第一步是利用线性化理论对该系统进行线性化。

4.1系统线性化

根据所建立状态方程的复杂性以及易于实现的程度，本研究采用泰勒级数逼近法对状态方程线性化。系统模型是具有如下形式的一组方程式：

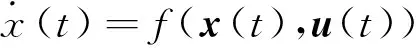
(24)

y(t)=g(x(t),u(t))

(25)

式中，x(t)是一个8×1的状态向量(Th、Tc、Tm、Ri、Hi、Re、Hm和φ)，u(t)是一个2×1的输入向量(Vp和Pin)，y(t)是一个关于衡量参数(Ri和Tm)的2×1输出向量。

根据泰勒级数展开式可以将系统线性化为标准状态空间模型，系数矩阵A(t)和B(t)分别是f对x(t)和u(t)求偏导的函数行列式，即：

A(t)=

CZ法晶体生长系统模型的输出方程为：

(26)

4.2系统特征值

系统的特征值定义为特征方程∏(λ)的根。表3给出了在不同的熔体高度Hm下两种模型的线性化系统的特征值。由于Hm每下降1cm对应大约20小时的晶体生长，因此，特征值随时间的增加几乎无变化。

表3　系统开环特征值

4.3系统稳定性

系统的特征值结果为该系统是不稳定系统提供了数据支持。从表3中可以看出，线性化的模型具有右半平面的特征值，这表明系统是不稳定的。

4.4系统可控性

为了确定仅在加热器功率作用下的系统是否可控，通过计算可控矩阵的秩进行判断。

在本文所建立的系统中，系统阶数是8，采用符号计算求解矩阵A的秩，结果为6，可以得出：仅在加热器功率作为输入的情况下系统是不可控的。由于本文所建立的线性化模型是时变的、高度耦合的复杂模型，因此不能采用常规PID算法设计控制器，相比之下采用易调整、能够系统解决约束和时延等实际问题的模型预测控制算法作为控制策略。

5　CZ法晶体生长系统的模型预测控制

模型预测控制(MPC)是一种基于模型的控制算法，包括经典模型预测控制和综合模型预测控制，利用内部模型的状态或输出预测，同时应用了有限时域的滚动计算思想和反馈及预测校正，最后采用了对某个系统性能指标的最优化计算以确定在一个控制时域内的最优控制序列。由于其鲁棒性强、抗干扰性强，而且能够在优化控制理论的框架内很好地处理系统的控制约束等特点，非常适用于实际工业过程的控制，而CZ法晶体生长过程本身便是一个典型的工业过程。

CZ法晶体生长过程的闭环控制系统初步设计如图8所示，其中r是参考轨迹，u是输入，y是输出，w、z是干扰。对于直拉法晶体生长系统，u是系统输入，即：加热器功率Pin和提拉速率Vp；y是系统输出，即熔体温度Tm和分界面半径Ri；w是加热器功率Pin上的干扰；z是分界面半径Ri上的干扰。

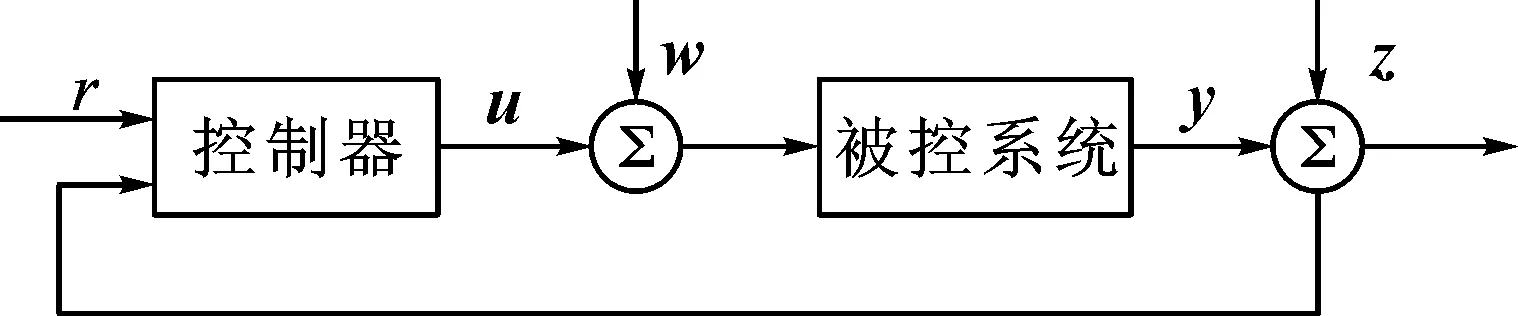
图8　闭环控制系统Fig.8　Closed loop control system

根据标称无延迟线性系统(即无干扰且不存在内部模型和被控系统的不匹配)设计无约束MPC控制器来研究系统性能。系统的激励给定为阶跃信号。

通过对预测时域、控制时域选择不同的取值，进行仿真实验，确定合适的参数。

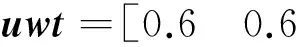
当设定熔体温度Tm为5K的阶跃激励、晶体半径Ri设定为常数0时，仿真结果如图10所示，这一结果也在可接受范围内。

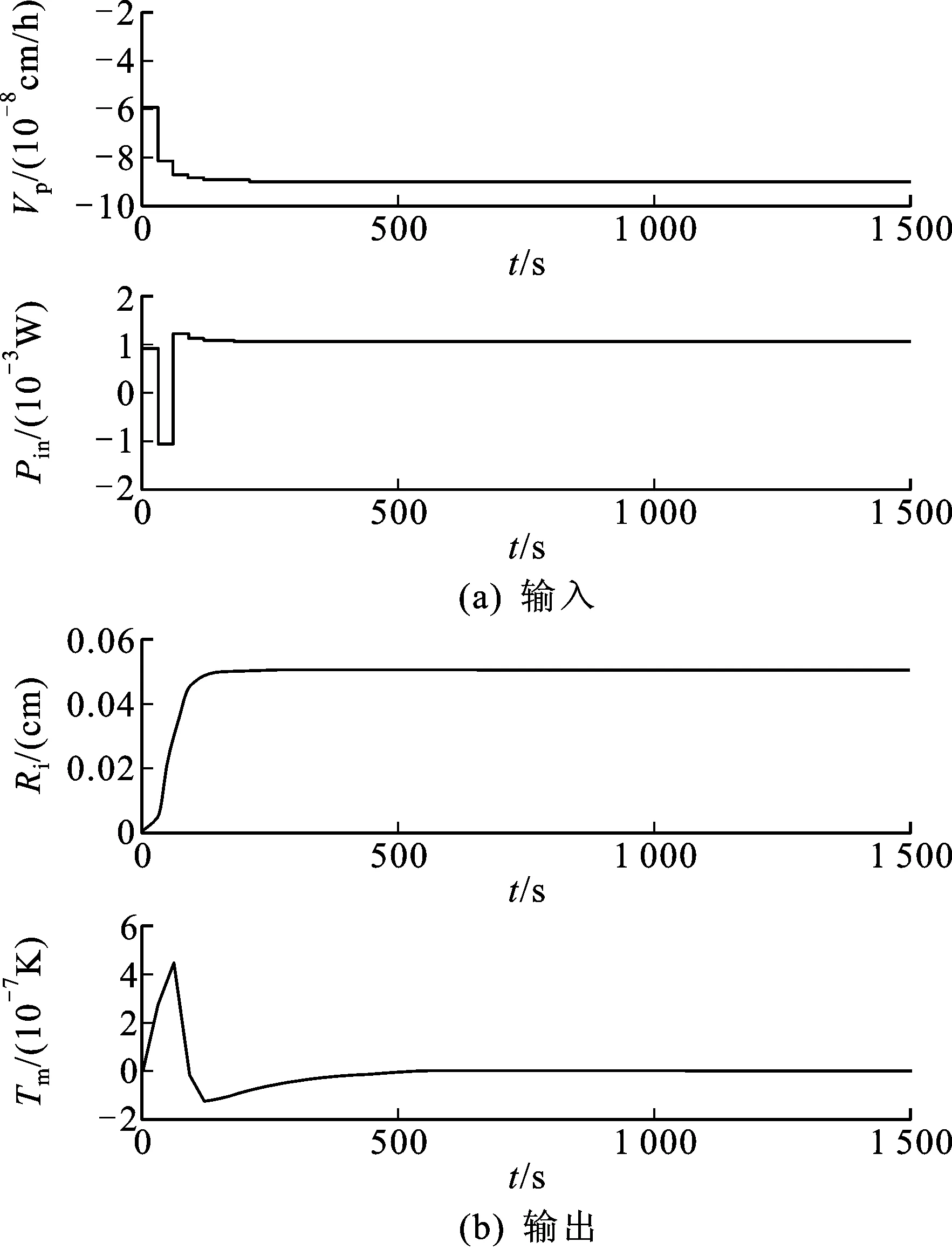
图9　Ri以0.5mm的步长变化时的系统响应Fig.9　Response to a 0.5mmstep change in Ri

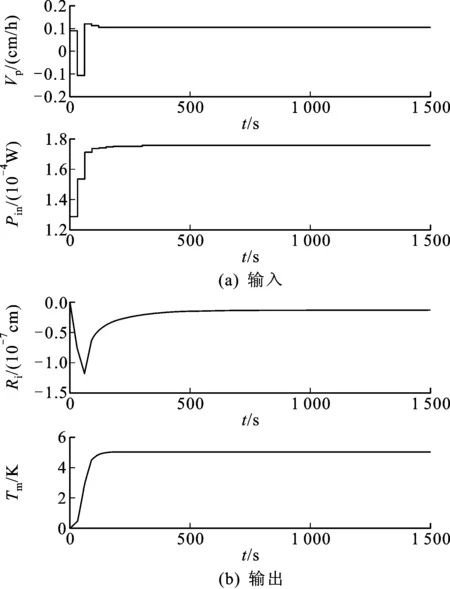
图10　Tm以5K的步长变化时的系统响应Fig.10　Response to a 5Kstep change in Tm

设计有延迟系统的控制器需要考虑在标称系统中加入时延，即考虑输入功率Pin到系统输出的纯时延，初步设定为60s。将预测时域P和控制时域M默认值下的无延迟结果与有延迟结果以及增加P和M取值的有延迟结果进行比较。当P和M取默认值且有延迟时，闭环系统无法执行并且是不稳定的；当P和M取值增加时，系统性能得以恢复。最后得出的仿真结果如图11所示，在可接受范围内，认为控制器性能良好。

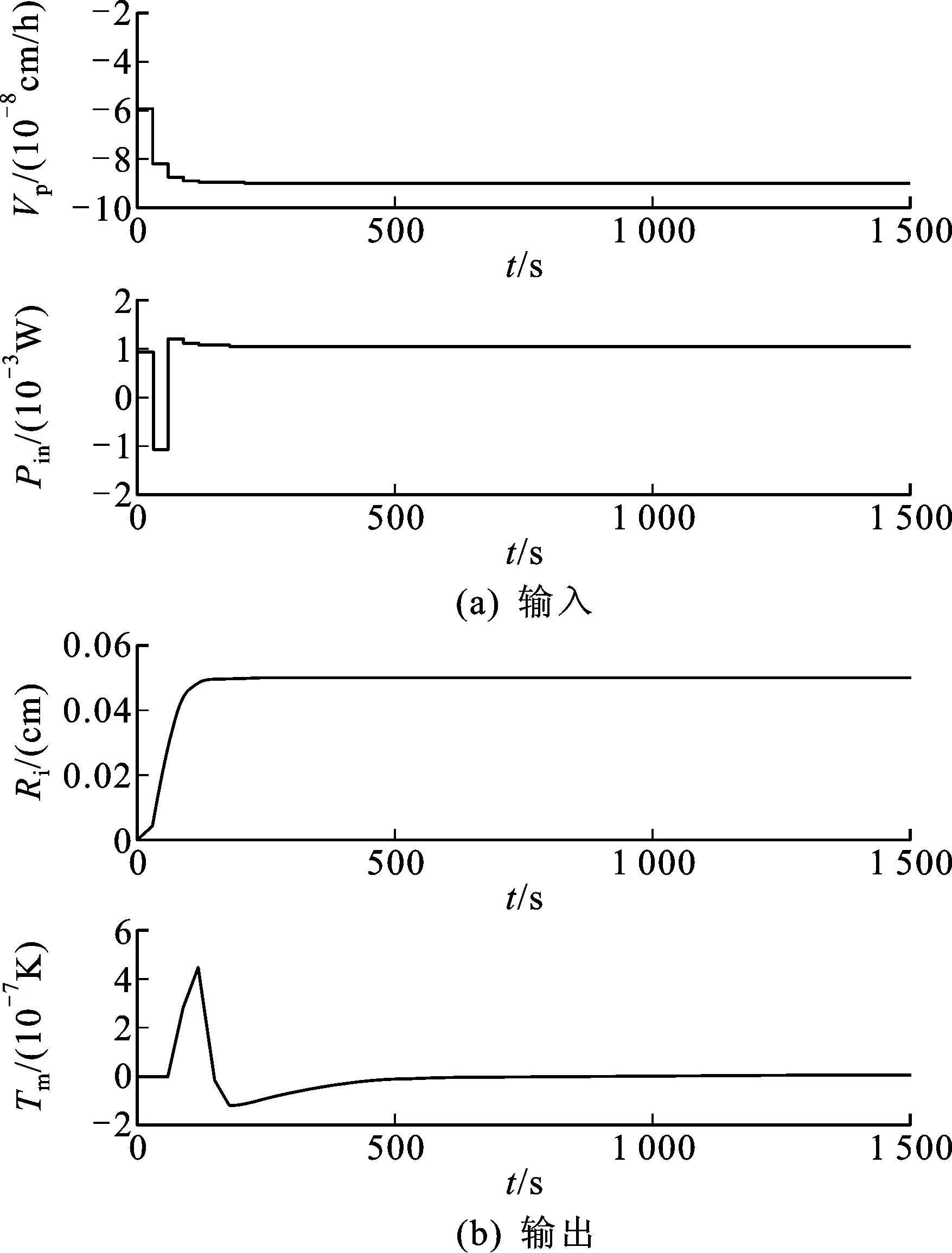
图11　Ri以0.5mm的步长变化时的系统响应，时延60 sFig.11　Response to a 0.5mmstep change in Ri, delay=60 s

6　结　语

本文基于传热传质基本原理建立了CZ法晶体生长等径阶段的低阶模型，并通过验证开环特征根的方式证明了模型的有效性，采用模型预测控制算法针对系统有无延迟的情况分别设计了相对应的无约束无干扰控制器，在可接受范围内，认为控制器的控制效果良好。本研究下一步将在控制器的设计中考虑约束和干扰的问题，进行更结合实际工业问题的研究。

[1] 徐赟瑜. 直拉法单晶硅熔体内热量动量及质量输运的数值模拟[D]. 重庆:重庆大学,2009:5.

XU Yunyu. Numerical simulation of heat, momentum and mass transport in the melt of Czochralski silicon single crystal[D]. Chongqing：Chongqing University,2009:5.

[2] DERBY J J, BROWN R A. Thermal-capillary analysis of Czochralski and liquid encapsulated Czochralski crystal growth II. processing strategies[J]. Journal of Crystal Growth，1986，75(2):227-240.

[3]DERBY J J, BROWN R A. Thermal-capillary analysis of Czochralski and liquid encapsulated Czochralski crystal growth: I.Simulation[J]. Journal of Crystal Growth，1986，74(3):605-624.

[4]DONALD T J H. Crystal pulling from the melt[M]. New York：Springer Verlag，1993.

[5]BRICE J C , BRUTON T M, HILL O F,et al. The Czochralski growth of Bi12SiO20crystals[J]. Journal of Crystal Growth, 1974,24-25:429-431.

[6]JONES D W. An experimental model of the flow in Czochralski growth[J]. Journal of Crystal Growth,1983, 61(2): 235-244.

[7]SEIDL A, MARTEN R, MTILLER G. In situ investigation of oxygen distribution and transport in Czochralski silicon melts by electrochemical solid ionic sensors[J]. Journal of Crystal Growth. 1996,166(1-4):680-684.

[8]GEVELBER M, George S. Dynamics and control of the Czochralski process I: Modeling and dynamic characterization[J].Journal of Crystal Growth, 1987, 84(4): 647-668.

[9]GEVELBER M, George S. Dynamics and control of the Czochralski process II:Objectives and control structure design[J].Journal of Crystal Growth,1988, 91(1-2): 199-217.

[10] GEVELBER M, George S. Dynamics and control of the Czochralski process III:Interface dynamics and control requirements[J]. Journal of Crystal Growth,1994, 139(3-4): 271-285.

[11]GEVELBER M, George S. Dynamics and control of the Czochralski process IV:Control structure design for interface shape control and performance evaluation[J]. Journal of Crystal Growth, 1994, 139(3-4): 286-301.

[12]SCHEEL H J. Historical aspects of crystal growth technology[J]. Journal of Crystal Growth, 2000, 211(1):1-12.

[13]蒋荣华,肖顺珍. 半导体硅材料的进展与发展趋势[J]. 四川有色金属，2000,(3)：1-7.

JIANG Ronghua,XIAO Shunzhen. Progress and development trend of semiconductor Si materials[J]. Sichuan Nonferrous Metals,2000,(3):1-7.

[14]张尚中.提拉法晶体生长全局数值模拟[D]. 重庆:重庆大学资源与环境科学学院，2009:4.

ZHANG Shangzhong. Global simulation of Czochralski crystal growth[D]. Chongqing: College of Resource and Environmental Science of Chongqing University，2009:4.

[15]MARTINEZ D M. Modeling and control of the Czochralski crystal growth process[D]. Texas: Texas A&M University,2002.

(责任编辑周蓓)

Modeling based on resistive network and simulation of MPC method on Czochralski growth process

YI Yingmin， ZHANG Tong

(School of Automation and Information Engineering, Xi’an University of Technology, Xi’an 710048,China)

For strong nonlinear with large delay on CZ growth process of silicon, the model based on the heat and mass transfer phenomenon is developed. The steady state solutions in the initial conditions are calculated, linearization and analysis of system model are conducted, with control algorithm and designing determined and the controller based on the controllability and stability of the system designed. It is concluded that the simplifications in radiation view factors given by Gevelber can reflect the characteristics of crystal growth in industry. Moreover, the analysis of system performance indicates that the system is uncontrollable and unstable on the premise of heater power as the input, thus using the model predictive control algorithm as the control strategy. Then the unconstrained MPC is designed for the nominal, delay-free, linearized system and the unconstrained MPC for the nominal, delay, linearized system, with the result that verifies the validity of these methods.

single-crystal silicon; the Czochralski process; the resistive network analogy; the lower order model; model predictive control

1006-4710(2016)02-0142-07

10.19322/j.cnki.issn.1006-4710.2016.02.003

2015-05-21

国家重点基础研究发展计划973项目资助(2014CB360508)；国家自然科学基金资助项目(61533014);陕西省教育厅科研资助项目(16JS069)

弋英民,男,教授,博士,研究方向为晶体生长模拟仿真研究。E-mail: yiym@xaut.edu.cn

O782+.5

A