中国城市能源效率测算
陈 龙,李金昌,程开明
(1.浙江工商大学 统计与数学学院, 浙江 杭州 310018;2.浙江财经大学 数据科学学院, 浙江 杭州 310018)
中国城市能源效率测算
陈龙1,李金昌2,程开明1
(1.浙江工商大学 统计与数学学院, 浙江 杭州 310018;2.浙江财经大学 数据科学学院, 浙江 杭州 310018)
摘要:伴随着中国的快速城市化进程,能源消耗总量不断攀升,其中城市能源消耗量占到绝大比重,故科学测算与认清城市能源效率状况,对于制定合理的能源政策具有重要意义。借助多渠道的统计数据和细致的数据预处理,文章在以永续盘存法估算城市资本存量的基础上,借鉴Zhou等(2012)基于Shephard能源距离函数的能源效率定义,将劳动和资本的无效率从生产函数中分离出来,采用随机前沿分析(SFA)测算我国2001-2013年245个地级以上城市的全要素能源效率,并开展四大地区、南方北方、不同规模等级城市全要素能源效率的差异分析。结果显示,地级以上城市能源效率平均水平略高于0.6,能源效率排名前10位城市主要位于东部沿海地区,后10位城市则主要位于西部地区;四大地区、南方北方及不同规模等级城市的能源效率及变动趋势表现出明显差异,总体上都存在较大的节能潜力空间。
关键词:城市资本存量;随机前沿分析;永续盘存法;城市全要素能源效率
一、 引言
伴随着中国城市化的快速推进,能源消耗总量不断上升,据《世界能源统计年鉴》显示,2010年中国超过美国成为世界上最大的能源消费国,面临的能源问题备受关注。《中共中央关于制定国民经济和社会发展第十三个五年规划的建议》提出“能源资源开发利用效率大幅度提高,能源消耗、碳排放总量得到有效控制,主要污染排放总量大幅减少”的目标,开展能源效率的讨论尤为必要。在全球总能耗中,城市所消耗的能源占到三分之二以上,城市排放的温室气体超过全球总额的70%[1]。鉴于未来几十年里新涌现的巨型城市还将对全球能源的需求及分配产生决定性影响[2],城市显然是节能减排的重心,提高城市能源效率成为节能减排的关键环节。因此,科学、准确地测算城市能源效率,了解我国城市能源效率现状及变动趋势,对于政府部门制定合理有效的能源政策,具有重要的现实意义。
世界能源委员会把“能源效率”定义为“能源的服务产出量与使用量(或投入量)的比值”[3];Patterson(1996)指出,能源效率本身是一个一般化的术语,可用多种数量上的指标进行测算,并认为能源效率是有用产出与能源投入的比值[4]。Bosseboeuf等(1997)将能源效率拓展为经济能源效率和技术能源效率,前者指用相同或更少的能源获得更多产出或更好生活质量,后者指由于技术进步、生活方式改变、管理完善等导致能源使用的减少[5]。对能源效率的概念与定义不同,相应的测算方法也存在差异。Hu和Wang(2006)把能源效率的计算方法概括为两种:一种是单要素能源效率,只把能源要素作为投入量,不考虑其他生产要素,主要包括能源消耗强度和能源生产率指标;二是全要素能源效率,即考虑各种投入要素相互作用的能源效率[6]324。单一指标存在一定的不全面性,未能考虑其他投入指标对能源的替代效应,而数据包络分析(DEA)和随机前沿分析(SFA)等方法适合在多要素生产函数理论框架下计算某种投入要素的利用效率。
进入21世纪,学者们利用DEA模型考察了中国省级或行业能源效率及其影响因素。Hu和Wang(2006)对中国各地区1995-2002年的多要素能源利用效率进行比较研究[6]328;Wang等(2014)利用全局DEA方法,从静态和动态两个角度分析2001-2010年中国省级能源效率[7];Zha等(2016)提出一种新的方法——机会约束DEA,并利用其测算出2010年中国区域能源使用效率和二氧化碳排放效率[8];杨红亮和史丹(2008)以2005年数据为基础对中国各地区的能源效率进行测算,表明多要素能效指标在揭示一个地区资源禀赋对能效的影响方面有着单要素方法不可替代的优势[9];李世祥和成金华(2008)应用不同目标情景下的能源效率DEA模型,从省际、工业行业面板数据的角度评价了中国能源效率[10];魏楚和沈满洪(2007)[11]、王强等(2014)[12]、张志辉(2015)[13]采用省区面板数据对中国区域能源效率时空差异特征及其影响因素进行了研究。
另外,部分文献利用SFA模型对能源效率进行了分析。Zhou等(2012)使用Shephard能源距离函数定义一种能源效率指数,并采用SFA方法估算2001年21个OECD国家的经济系统能源效率[14]199;赵金楼等(2013)在随机前沿分析框架下,测算出我国1980-2010年29个省市自治区的能源效率,并对能源效率地区差异、影响因素、收敛性等进行分析[15];林伯强和杜克锐(2013)利用面板数据的固定效应SFA模型对我国1997-2009年省际能源效率进行测算,并就要素市场扭曲对能源效率的影响进行探讨[16];Lin等(2014)在异构技术下,采用潜类别随机前沿方法测度1997-2010年中国省级能源效率,结果表明省级总体能源效率不高[17];Lin等(2015)还采用基于超越对数函数假设的SFA模型分析2005-2011年中国化工行业能源效率和节能潜力[18]。
世界能源消耗总量中城市能耗占绝大比重,中国城市能源消耗同样占到总能耗的75%,城市居民人均能源消耗量是农村居民的6.8倍[19]4208,城市在能源消耗和温室气体排放中起着举足轻重的地位,需要重点测算城市能源效率。Keirstead(2013)利用英国198个城市数据,通过比率指标、回归残差和DEA等三种方法对城市能源效率进行测算,比较了各自的优势与不足[20];美国能源效率经济理事会(ACEEE,2013)考虑包括地方政府运营、社区积极性、建筑政策、能源和水利用政策、交通政策等五个方面的指标而编制了美国34个城市的城市能源效率记分卡[21];Mao等(2010)采用单一指标方法对中国三个主要城市重庆、广州和天津的39个工业行业能源效率进行了估计[22]。
一些学者对中国部分城市的能源效率进行了分析。张伟和吴文元(2011)对长三角都市圈城市群1996-2008年全要素能源效率及其成分进行了测度和因素分析[23];史红亮和杨先明(2015)在环境规制的视角下,基于DEA方法对云南省六大城市群16个州市2005-2013年间的全要素能源效率进行测算,并对州市间的能源效率差异和节能潜力进行分析[24];李治和李国平(2010)利用DEA模型,运用1995-2006年中国210个地级市的面板数据测算城市全要素能源效率,并分析了城市全要素能源效率差异特征[25]。
综观已有测算能源效率的文献,发现部分文献混淆了能源生产率和能源效率这两个不同的概念,能源效率的测度大部分以国家、省份、行业或局部城市为研究对象,缺少对全国地级以上城市能源效率的测算;能源效率的测度多采用DEA方法,无法考虑随机因素对测算结果的影响,一些测算对城市能源效率的关键投入指标——城市资本存量的数据来源语焉不详。基于此,本文结合多渠道数据,在采用永续盘存法准确估算城市资本存量的基础上,借鉴Zhou等(2012)定义的基于Shephard能源距离函数的能源效率,将劳动和资本的无效率从生产函数中分离出来,利用随机前沿分析(SFA)方法测算2001-2013年全国245个地级以上城市全要素能源效率,分析其分布特征及变动趋势。
与现有文献相比,本文的创新主要体现在以下三个方面:(1)厘清能源生产率和能源效率的关系,定义了能将劳动和资本投入要素的无效率分离出来、真正反映能源投入效率的能源效率;(2)获取资本存量数据是测算能源效率的前提之一,采用永续盘存法细致地估算出2001-2013年全部地级以上城市的资本存量,而不是选取替代变量,提高了能源效率测算结果的可信度;(3)以全国地级以上城市为研究对象,采用SFA方法能够有效考虑随机因素对能源效率的影响,使能源效率的测算结果更符合实际。
二、 城市能源效率测算方法
(一) 全要素能源效率
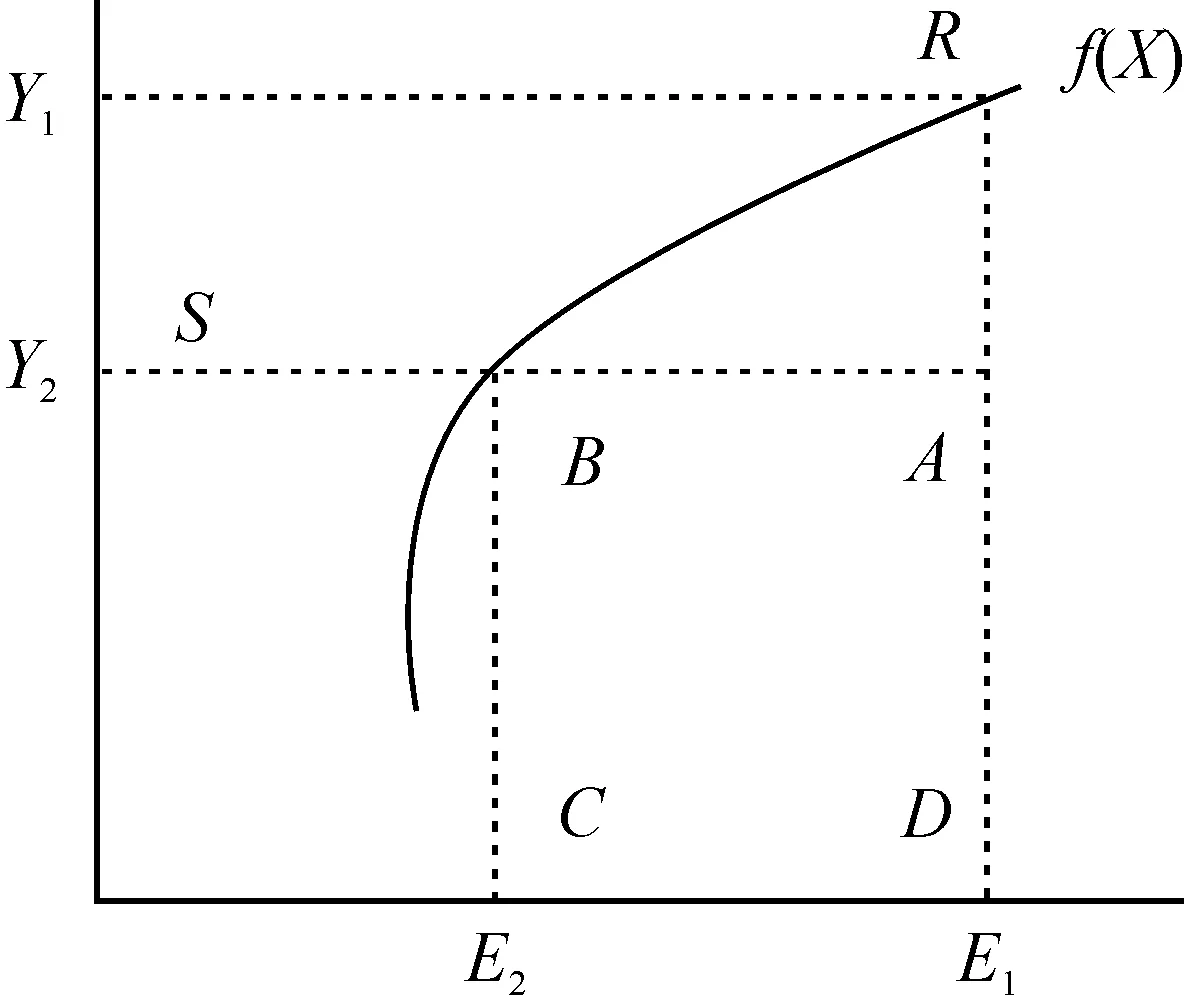
图1 能源生产率和能源效率
测算城市全要素能源效率之前,需先厘清能源生产率和能源效率的关系[26]68。生产率指生产过程中产出与所需投入的比率,可分为单要素生产率、多要素生产率或全要素生产率。单要素生产率是指产出与某一投入要素的比率,多要素生产率是产出与对各投入要素根据一定权重进行加总后得到的投入比率。效率通常包括技术效率和配置效率[27],技术效率可从投入和产出角度来衡量,即产出既定情况下,投入最小化的程度,或投入既定情况下,产出最大化的程度;配置效率是反映给定各自价格的情况下,投入(或产出)实现最优比例的能力。本文能源效率指的是能源的技术效率,能源生产率和能源(技术)效率的关系如图1[26]69。
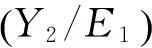

所谓全要素能源效率,是指在包含多种投入要素的分析框架下计算能源投入要素的利用效率,参考图1,即衡量产出不变时,点A距离生产前沿面最优点B的距离和程度。全要素能源效率用公式表示如下:

(1)
综合来看,全要素能源效率测算需解决两方面的问题:一是生产前沿面的确定,二是相对距离的测度。相对距离的测度主要采用Shephard(1970)[28]定义的基于投入、产出角度的距离函数,生产前沿面的确定方法包含参数法和非参数法两种。非参数法通过数据驱动形成一条线性包络面作为前沿面,不涉及参数函数的估计,但不能像参数方法有统计检验数作为样本拟合度和统计性质的参考,且误差项的部分不能解释随机扰动部分,而参数型前沿生产函数,围绕误差项的确定,通过先验的生产函数进行参数估计,将函数中的误差项划分为技术无效项和随机误差项,更能体现样本的统计特性,也反映了样本计算的真实性。
非参数方法中,最典型的是Farrell(1957)[29]提出的数据包络分析(DEA);参数方法中,确定生产函数时一般选择C-D生产函数、CES函数或Translog函数等,具体包括收入份额法、计量经济法和随机前沿分析等,其中随机前沿分析(SFA)最具有代表性。与DEA方法相比,SFA方法能够解释随机扰动项;此外,随机前沿模型中生产前沿面是随机的,应用于面板数据研究的结论更加接近现实。
综上所述,能源生产率和能源效率为不同的概念,本文的城市能源效率指的是城市全要素能源技术效率,并选择随机前沿分析(SFA)模型来加以测算。
(二) 随机前沿分析(SFA)模型
1977年,Meeusen和Breck、Aigner等以及Battese和Corra发表三篇关于SFA的学术论文,标志着随机前沿分析方法的正式诞生[30]148,他们提出以下形式的随机前沿面生产函数:
yi=f(xi,β)exp(vi-ui)=f(xi,β)exp(vi)×exp(-ui)
(2)
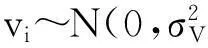
1.生产函数模型选择。使用SFA来测度城市全要素能源效率之前,首先需设定模型所需要的生产函数。SFA方法常用的生产函数包括线性生产函数、柯布-道格拉斯生产函数(C-D生产函数)、列昂惕夫生产函数、固定替代弹性生产函数(CES生产函数)和超越对数生产函数(Translog生产函数)等。
因柯布-道格拉斯生产函数可线性化,容易进行数学处理,每个参数具有明确的经济含义,且在测算各因素对增长的贡献率方面具有其他生产函数无法替代的优势,在此选择C-D生产函数作为模型所需生产函数进行估计。为方便在线性回归框架下对生产函数模型中的参数进行估计,等式两边取对数的C-D生产函数模型为:
(3)
2.技术无效性。在随机前沿模型中,复合残差项εi=vi-ui,为了方便说明上述C-D生产函数模型,先限定只有唯一的投入xi获得产出qi,在这一前提下的柯布-道格拉斯随机前沿面模型可表示为:
lnqi=β0+β1lnxi+vi-ui或
(4)
qi=exp(β0+β1lnxi+vi-ui)=exp(β0+β1lnxi)×exp(vi)×exp(-ui)
其中,exp(β0+β1lnxi)为确定部分,exp(vi)为随机误差项部分,exp(-ui)为无效率部分。
则技术效率的测度方法是计算观测产出与相应的随机前沿面产出的比值:
(5)
因为ui≥0,所以exp(-ui)∈[0,1],即技术效率取值范围为[0,1]。
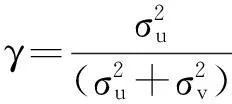
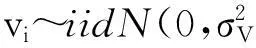
4.面板数据SFA模型。上述讨论的随机前沿分析模型主要针对截面数据,在此将SFA模型扩展到面板数据。与截面数据相比,面板数据可以反映每个生产决策单元在一段时间内的连续表现,包含更多的观测点,可提供更加精确的信息。对应式(2)面板形式的随机前沿面生产函数可表示为:
yit=f(xit,β)exp(vit-uit)
(6)
(三) 基于城市全要素能源效率的SFA模型
已有文献所定义的能源效率大多数是指能源生产率,即包含所有生产要素(资本、劳动、能源)的综合利用效率,本文基于能源生产率和能源效率的区别,如式(1)定义的能源效率,将劳动和资本的无效率分离出来,只反应能源这一投入要素的效率,以便准确地获知现实经济中的能源利用效率和节能潜力空间。
Zhou等(2012)[14]197假设在新古典部门生产框架下,资本(K)、劳动(L)、能源(E)为投入,生产总值(Y)为产出。从概念上来看,生产可能集表述如下:
T={(K,L,E,Y):(K,L,E)能生产出Y}
(7)
在生产理论中,T被假定为有界集和闭集。此外,投入和产出被假定满足强可处置性,即如果(K′,L′,E′)≥(K,L,E)且Y′≤Y,则(K′,L′,E′,Y′)∈T。
为从生产效率角度来测度能源效率,定义基于投入能源的Shephard距离函数为:
(8)
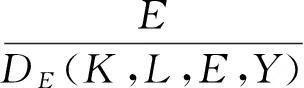
(9)
当某被评价单元位于生产前沿面时,该单元的能源效率值等于1,即能源效率有效;当某被评价单元偏离生产前沿面时,该地区的能源效率值小于1,即该被评价单元的能源投入没有得到充分利用,存在帕累托改进空间;某地区能源效率值越大表示该地区能源利用效率越高。
假设现有i=1,2,...,n个城市,城市i有投入和产出向量(Ki,Li,Ei,Yi),则城市Shephard能源距离函数可表示为DE(Ki,Li,Ei,Yi)。利用SFA模型来估计DE(Ki,Li,Ei,Yi),需要确定具体的生产函数形式,本文选择柯布-道格拉斯生产函数(C-D生产函数),则相应的能源距离函数为:
lnDE(Ki,Li,Ei,Yi)=β0+βKlnKi+βLlnLi+βElnEi+βYlnYi+vi
(10)
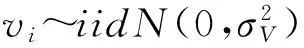
因为Shephard能源距离函数是关于能源E的线性齐次方程,则有:
DE(Ki,Li,Ei,Yi)=EiDE(Ki,Li,1,Yi)
(11)
这意味着
lnDE(Ki,Li,Ei,Yi)=lnEi+lnDE(Ki,Li,1,Yi)
=lnEi+β0+βKlnKi+βLlnLi+βEln1+βYlnYi+vi
(12)
联立式(10)和式(12),得
βE=1
(13)
将式(13)代入式(10),得
(14)
其中,ui=lnDE(Ki,Li,Ei,Yi)≥0为单边误差项,表示城市i生产活动的能源无效率。
式(14)SFA模型形式是针对横截面数据的,将其拓展为面板数据形式的SFA模型为:
(15)
在随机误差项vit和单边误差项uit分布假设的基础上,用极大似然法(ML)对式(15)的各参数系数进行估计,可得出各城市每年的能源无效率部分uit以及各城市每一年份的能源效率值EEIit=exp(-uit)。
三、 变量选取及数据来源
(一) 变量选取
城市能源效率SFA模型中的产出变量以各城市的地区生产总值(Y)代表,转换为以2001年为基期的不变价生产总值,并假定生产过程中需要三种投入要素即资本(K)、劳动力(L)和能源消耗量(E)。
对于资本(K),我国目前还没有公开的官方资本存量数据,需要对其进行估算。对于资本存量的估算,现有大部分研究侧重于估算整个国家或省域层面的资本存量,其中王益煊等(2003)[31]41、孙琳琳等(2005)[32]、钱雪亚等(2009)[33]40估算了全国资本存量,张军等(2004)[34]、单豪杰(2008)[35]18等则对省际资本存量进行了估算。综合现有文献和数据可得性,在此以永续盘存法开展2001-2013年中国地级以上城市的资本存量估算,基本公式为Ki,t=Ii,t+Ki,t-1(1-δi,t),其中Ki,t表示第i个城市第t年资本存量,Ii,t表示为第i个城市第t年投资额,Ki,t-1表示第i个城市第t-1年资本存量,δi,t表示第i个城市第t年经济折旧率[36][37]15,其中涉及四个关键变量:投资额、固定资产投资价格指数、折旧率和基年资本存量,这四个变量的具体测算下文将做详细说明。
劳动力(L)本应以全国就业人员的有效劳动时间衡量,但缺乏平均工作时间的统计数据,故采用各个城市的“年末单位从业人员数”替代。对于能源消费量(E),目前我国已有各个省份能源消费总量的公开资料,而城市能源消费的公开数据仅限于城市用电、煤气和液化石油气消费量,未公开煤炭、石油等指标数据,所以只能以推算方式得到城市能源消费总量。借鉴Dhakal(2009)[19]4211的方法,城市能源消耗量UE=UGRPi,t×EIi,t,其中UGRPi,t表示城市i第t年的地区生产总值,EIi,t表示城市i第t年的能源强度,并假定城市i的能源强度与该城市所属省份的能源强度相等,如此推算出各城市能源消耗量。
统计上,城市通常包括“全市”和“市辖区”两个口径,测算城市能源效率须先明确城市的范围,市辖区是城市功能及特征的主要集中地,故本文将城市范围限定为“市辖区”,以区别于“全市”口径。鉴于我国能源消费指标和一些相关指标的公开数据多到地级市一级,县级市的数据很不完整,故以地级以上城市为样本。
为保持研究样本的一致性,剔除2001-2013年期间因行政区划调整导致前后不可比以及相关指标数据缺失的城市,最终以余下的245个地级以上城市作为研究对象。譬如,从2012年起,《中国城市统计年鉴》不再公布巢湖市的统计数据;2001-2013年行政区划发生变化的城市还包括盘锦市、葫芦岛市、双鸭山市、大庆市、七台河市、牡丹江市、黑河市、毫州市、莆田市、荆门市、佛山市、潮州市等。
(二) 数据来源
2001-2013年245个地级以上城市的“固定资产投资总额”和各城市“地区生产总值”(GDP)来源于《中国城市统计年鉴》(2002-2014年)。当某个城市某一年份的指标数据明显偏大或偏小,可能为异常值时,先检查该年份城市的行政区划是否发生变动,然后查询该城市所在省份和该城市的统计年鉴以核实指标数值。
2001-2008年各省(市、自治区)“固定资产投资价格指数”来源于《新中国60年统计资料汇编》,2009-2013年该指标数据来源于《中国统计年鉴》(2010-2014年)。
2001-2013年地级以上城市的“年末单位从业人员”数据均来源于《中国城市统计年鉴》(2002-2014年),同样利用上述固定资产投资与地区生产总值异常值处理方法对一些城市的异常数据进行相应处理。
2001-2008年各个省份的“地区生产总值”及“地区生产总值指数”来自于相应年份的《中国统计年鉴》,2009-2013年的数据来源于《中国统计年鉴(2014)》。2001-2008年各省份“能源消费总量”数据来源于《新中国60年统计资料汇编》,2009-2013年各省份“能源消费总量”数据来源于《中国能源统计年鉴(2014)》,其中缺失湖南省2001-2004年能源消费量数据,根据《中国能源统计年鉴(2007)》补齐。
四、 城市全要素能源效率的测算及分析
(一) 城市资本存量估算
资本存量是进行能源效率测算的前提之一,利用永续盘存法估算2001-2013年中国地级以上城市的资本存量,涉及投资额、固定资产投资价格指数、折旧率和基年资本存量四个关键变量的测算。
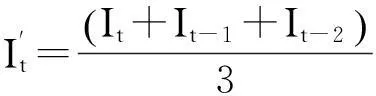
2.固定资产投资价格指数。估算城市资本存量的基年为2001年,为得到其他各年份的资本存量,还需消除固定资产价格变动带来的影响。《中国统计年鉴》从1993年开始公布各个省份的固定资产投资价格指数,在此将各年份的固定资产投资价格指数转化为以2001年为基期的定基价格指数,并假定各城市固定资产投资价格指数与其所在省份的固定资产投资价格指数相同。
3.折旧率。资本存量的估算结果对折旧率也相当敏感,折旧率的准确估计同样重要。从已有文献看,关于固定资产折旧的处理方式包括三种:(1)主观假定某一折旧率水平;(2)利用国民经济的平衡关系间接推算折旧指标,如Chow(1993)利用恒等式(折旧额=GDP-国民收入+补贴-间接税)推算出折旧额[41];(3)按照各类固定资产的经济寿命来确定折旧率水平,此为大部分研究所采用的折旧率估计方法。由于我国固定资产投资数据序列时期较短,因而采用几何折旧方式计算城市固定资产折旧额时,假定固定资产价值每年按同一比例递减,折旧率等于重置率且为常数,即有
dT=(1-δ)T,T=0,1,…
(16)
其中,dT表示资本品的相对效率;T表示时期;δ表示折旧率。在此以我国法定固定资产残值比例来代替资本品的相对效率,《中国人民共和国企业所得税暂行条例及实施细则》第三十一条规定固定资产残值比例统一为5%。《中国统计年鉴》中各地区固定资产投资按构成分三部分:建筑安装工程、设备工器具购置及其他费用,由于这三类资产存在明显的寿命差异,须先利用各自的寿命期计算折旧率然后加权平均得到总折旧率。关于固定资产的使用寿命,借鉴单豪杰(2008)使用的财政部《国有企业固定资产分类折旧年限表》确定相应的折旧年限[35]30,即建筑安装工程40年,设备工器具购置16年,进而根据式(16)计算得到建筑安装工程的折旧率为7.22%,设备工器具购置的折旧率17.08%。至于三类资产折旧率的权重,根据柯善咨(2012)的研究使用城镇固定资产投资中建筑安装工程和设备工器具购置两大类投资的比重估算[42]21,其中其他费用按照前两部分投资的比例摊入到两类投资中。利用计算出的权重得到该省(市)的加权总折旧率,并假定同一省份内各地级以上城市的折旧率与该省份固定资产加权总折旧率相同。
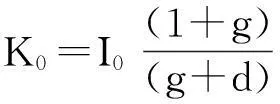
5.资本存量的估算结果。以测算的投资额、固定资产投资价格指数、折旧率和基年资本存量数据为基础,采用永续盘存法估算得到2001-2013年我国245个地级以上城市的资本存量数据,部分年份数据的描述性统计量见表1*受篇幅所限,未能将全部城市资本存量数据呈现,感兴趣的读者可向作者索取。。
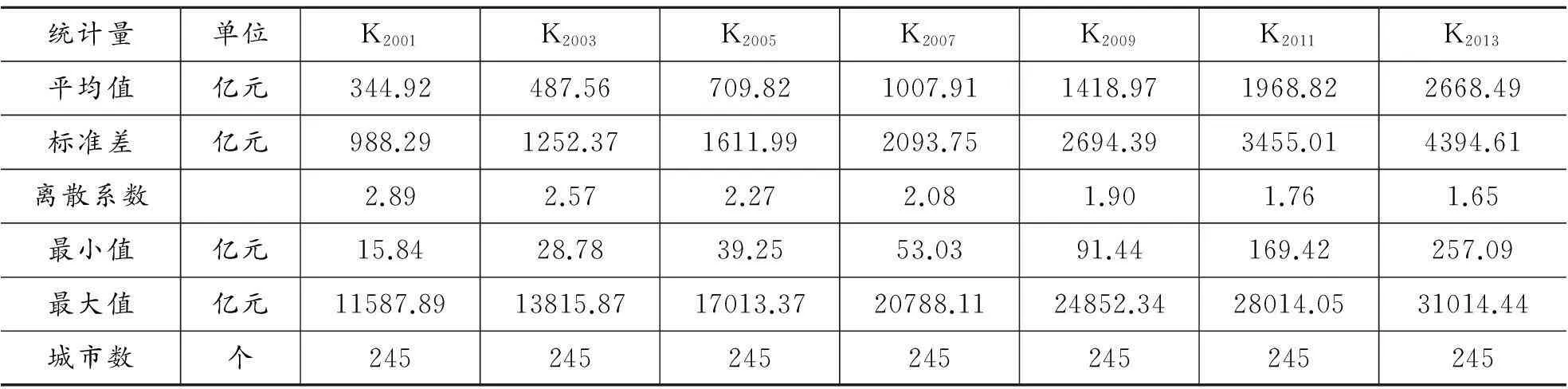
表1 资本存量序列的描述统计量
随着时间变动,城市资本存量的最小值、最大值和平均值均呈现逐步递增的趋势。最小值由2001年的15.84亿元增加到2013年的257.09亿元,最大值由11587.89亿元增加到31014.44亿元,资本存量均值由344.92亿元递增到2013年的2668.49亿元。而离散系数呈现逐步递减的规律,由2001年的2.89递减至2013年的1.65,说明随着时间变动,城市资本存量的离散程度不断减小,不同城市间资本存量的差距在缩小。
(二) 城市全要素能源效率的测算结果
依据各个城市的资本存量、年末单位从业人员数、能源消耗总量和地区生产总值数据,进一步测算城市能源效率,首先确定式(15)的单边误差项ui,t的分布。在实际运用中,简单的分布形式较为可行且易于控制[30]155,因此,本文对于ui,t分布的假设选择半正态分布和截断正态分布两种形式,接着利用最大似然法(ML)来估计式(15)的SFA模型,得到模型估计结果见表2。

表2 SFA模型的估计结果
注:*、**、***分别表示在10%、5%、1%的水平下显著,括号内为标准误。
表2中模型(1)为单边误差项uit服从半正态分布的估计结果,模型(2)为单边误差项uit服从截断正态分布的估计结果。模型(1)中的βL未通过10%水平下的显著性检验,而模型(2)中所有的系数都通过1%的显著性水平检验,故认为单边误差项uit服从截断正态分布的效果更好。单边误差项uit的LR统计量在1%的显著性水平下拒绝γ=0的假设,说明模型的误差项εi,t确实存在包含随机误差项vit和单边误差项uit的复合结构;γ为0.963表示随机前沿生产函数的误差中96.3%来源于技术非效率,其余3.7%的误差来自于不可控的随机因素。可见,采用随机前沿分析(SFA)对生产函数估计是合适的,模型(2)具有较高的可信任度。
接着,在确定单边误差项ui,t服从截断正态分布的基础上,依据式(15)的SFA模型,将所有的投入变量、产出变量数据导入软件Frontier4.1,得到全国2001-2013年245个城市的全要素能源效率,各年份的描述性统计量见表3。
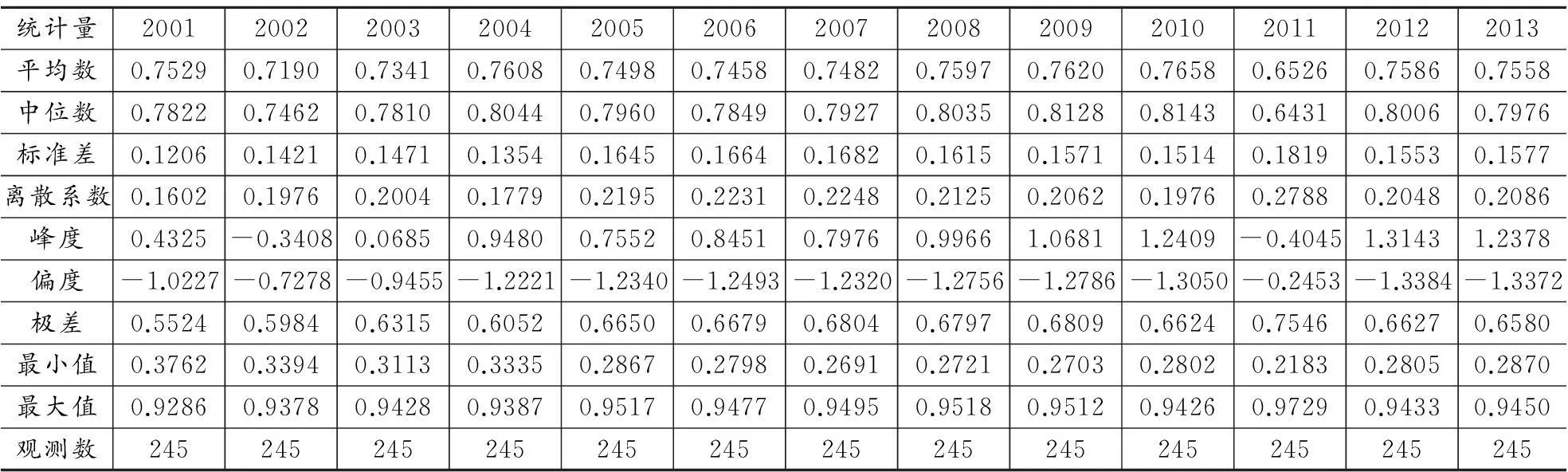
表3 各年份城市全要素能源效率的描述性统计量
从城市能源效率的均值来看,2001-2013年期间变动范围为0.6526-0.7658,呈现三个变化阶段:2001-2004年为第一个阶段,呈U型变动轨迹,2002年为低谷期;2004-2010年为第二个阶段,各年份能源效率值变动较小,处于平稳态势;2010-2013年为第三阶段,仍呈U型态势,其中2011年的能源效率值为所有年份的最小值,这可能与当年城市第二产业占生产总值的比重高于其他年份有关。
2013年245个地级以上城市的全要素能源效率均值为0.7558,没有城市的能源效率处于前沿面上,其中122个城市的全要素能源效率处于[0.8,1.0)范围内,92个城市的全要素能源效率在[0.6,08)范围内,18个城市的全要素能源效率处于[0.4,0.6)范围内,全要素能源效率在0.4以下的城市13个,可见全国多数地级以上城市的全要素能源效率远小于1,离效率前沿面有较大的距离,城市全要素能源效率的提升具有较大空间。
从城市能源效率的离散程度来看,2001-2007年能源效率离散系数,总体上呈递增趋势,表明城市之间的能源效率差异逐渐扩大;除2011年,2008-2013年的能源效率离散系数变化不大,城市之间的能源效率差距整体上在缩小。
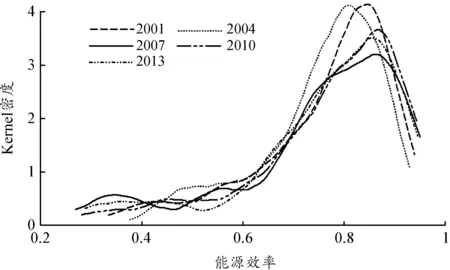
图2 城市能源效率核密度曲线
此外,考察245个城市中能源效率排名前10位和后10位的城市及变动情况,全要素能源效率排名前10位的城市绝大多数位于东部沿海地区,包括广东、江苏、福建和浙江等地,能源效率范围为[0.8998,0.9729];而排名后10位的城市几乎都位于西部地区,包括云南、宁夏、新疆、贵州等地,能源效率范围为[0.2183,0.4711],说明西部地区城市能源利用效率较低、节能潜力巨大。
进一步利用非参数核密度估计方法直观描述城市能源效率分布形态,绘制城市全要素能源效率的Kernel密度曲线,见图2。城市能源效率的核密度曲线整体上呈现出明显的左偏分布形态,峰值处于0.8-0.9之间,说明多数城市能源效率离效率前沿面还有一定距离。结合偏度系数和峰度系数看,2001-2013年的城市能源效率均呈现出明显的左偏分布和平顶峰度。
核密度图中,顶峰完全位于0.5右侧。2001-2013年,随着时间的推移,顶峰总体上向右移动;核密度图形顶峰随着时间的推移在逐渐下降,形态变得扁平,表明城市之间能源效率的差距有所缩小。
(三) 城市能源效率的差异分析
1.地区之间的差异。为反映城市能源效率的地区间差异,分东部、中部、西部和东北四大地区分别计算2001-2013年的城市全要素能源效率均值,得到不同地区城市能源效率的变动趋势见图3。
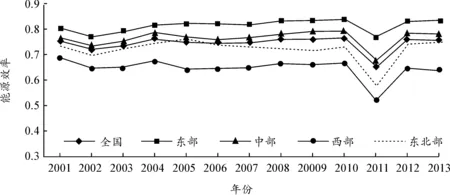
图3 不同地区全要素能源效率变动趋势资料来源:由测算的各年份城市全要素能源效率值整理而得。
从四大地区城市全要素能源效率值的变动范围来看,东部为[0.7657,0.8347],中部为[0.6762,0.7927],西部为[0.5210,0.6850],东北为[0.5770,0.7584],东部地区城市能源效率明显高于全国平均水平,中部地区城市能源效率略高于全国平均水平,而东北与西部地区的城市能源效率均低于全国平均水平。东部地区城市能源效率较高可能与其经济发展水平、技术水平、资源配置水平及产业结构层次较高有关;东北、西部地区城市能源效率普遍较低可能与其经济发展水平、技术水平及产业结构层次较低有关。例如,东部地区注重创新和新技术的应用,积极开发新能源,城市能源效率自然高于其他地区,而东北及西部地区的产业结构偏向资源型行业以及重化工业导致东北、西部城市能源效率低下。从离散系数(CV)来看,CV东北 2.南方北方城市的差异。以秦岭-淮河一线为界,以北的城市划分为“北方城市”,以南的城市划分为“南方城市”,245个地级以上城市中“北方城市”106个和“南方城市”139个,2001-2013年的“北方城市”、“南方城市”的能源效率均值见表4。 表4 北方、南方城市全要素能源效率比较 从表4可知,南方城市全要素能源效率显著高于北方城市,可能与南方、北方在资源分布、气温、产业结构等方面的差异有关。中国北方煤炭、石油、矿产等资源丰富,形成以采矿、冶金、机械制造等重工业为主的工业结构,而东南沿海地区虽然资源匮乏,但交通便捷、资金技术力量雄厚,发展原料、燃料消耗较少的工业类型,因而轻工业相对比较发达。重工业能耗高、多污染,自然导致北方城市能源效率相对低下,而轻工业以及技术进步等优势致使南方城市能源效率相对较高。另外,南方、北方自然气候差异明显,北方城市冬季供暖需要消耗大量能源可能对城市能源效率产生较大的影响,供暖城市通常能耗高、污染重,也相应导致能源效率低下。若从城市能源效率的排名来看,排名前10位的城市大多数为南方城市,排名后10位的城市大部分为北方城市。 3.不同规模等级城市的差异。地级以上城市可根据城市规模大小而划分为不同的规模等级,进一步考察不同规模等级城市全要素能源效率差异。根据2014年10月国务院发布的《关于调整城市规模划分标准的通知》,以2013年各地级以上城市的市辖区年末人口数为基准,将245个城市划分为小城市(50万人以下)、中等城市(50-100万人)、大城市(100-500万人)、特大城市(500-1000万人)和超大城市(1000万人以上)五个规模等级,城市数量分别为38、95、100、9和3个。为反映不同规模等级城市的能源效率差异,分别计算小城市、中等城市、大城市、特大城市和超大城市全要素能源效率平均值,见表5。 表5显示,2001-2013年小城市全要素能源效率值的变动范围为[0.6631,0.7592],中等城市能源效率的变动范围为[0.6484,0.7674],大城市能源效率的变动范围为[0.6516,0.7670],特大城市能源效率的变动范围为[0.6250,0.7761],超大城市能源效率的变动范围为[0.7695,0.8759]。总体来看,小城市的能源效率最低,超大城市的能源效率最高。特别是2001-2006年期间,随着城市规模等级变大,城市能源效率呈现递增态势,即城市规模越大,能源效率越高;而随着城镇化和工业化的快速推进,2007-2013年小城市和中等城市的能源效率有所提升,而大城市和特大城市的能源效率变动不大,导致城市规模等级与能源效率之间的正相关性不明显。结合2013年城市规模与能源效率的散点图发现,直观上两者之间存在着非线性关系,即可能存在一个最优城市规模使城市能源效率达到最佳,当然这有待于进一步深入探析。 表5 不同规模等级城市的能源效率 五、 结论、启示及展望 本文根据多渠道的统计数据,采用永续盘存法估算了城市资本存量。以其为基础,借鉴Zhou等(2012)定义的基于Shephard能源距离函数的能源效率,将劳动和资本的无效率分离出来,采用随机前沿分析(SFA)测算我国2001-2013年245个地级以上城市全要素能源效率,并开展城市全要素能源效率分地区、南方北方、规模等级的差异分析。结果表明:(1)随着时间变动,城市资本存量呈逐步递增的趋势,城市之间的差异不断缩小。城市资本存量均值由2001年的344.92亿元递增到2013年的2668.49亿元,最小值由2001年的15.84亿元增加到2013年的257.09亿元,最大值由11587.89亿元增加到31014.44亿元;城市资本存量的离散系数由2001年的2.89递减至2013年的1.65,不同城市之间的差距逐步缩小。(2)我国地级以上城市能源效率的变动呈现出阶段性特征,全要素能源效率多小于1,具有较大的提升空间。2001-2013年地级以上城市全要素能源效率的均值变动范围为0.6526~0.7658,表现出三个不同的变化阶段,绝大部分城市能源效率未处于前沿面上,意味着未来具有较大的潜力空间。(3)四大地区、南方北方和不同规模等级的城市能源效率具有明显差异。四大地区的城市能源效率呈“东部最高,中部次之,东北部较低,西部最低”的梯度分布特征;城市能源效率前10位城市主要位于东部沿海地区,后10位城市主要位于西部地区;南方城市的能源效率明显高于北方城市;总体上城市规模越大,能源效率越高,但两者之间可能存在非线性关系。 了解地级以上城市能源效率的现状、差异及变动趋势,对于后续开展城市能源效率的效应分解及影响因素分析奠定良好基础,也为制定合理的城市能源政策提供了客观依据。上述结论具有以下政策启示:第一,遵循地区差异原则、有针对性地深入推进节能降耗工作,推动社会经济绿色可持续发展。鉴于城市能源效率还存在较大提升空间且不同地区呈现出明显差异的现状,应充分考虑地区之间的不平衡性,针对不同地区出台差异化节能减排政策,完善节能减排目标管理体系,合理确定不同地区的节能降耗目标责任,以实现资源的节约和能源高效利用。第二,促成合理的城市规模分布体系,提高能源的综合利用效率。不同规模城市的能源效率存在明显差异,两者之间不存在单一的线性关系,为提升整体城市能源效率,应尊重城市发展规律,明确不同规模城市的功能定位,形成合理的城市规模分布体系,以充分发挥城市聚集经济效应,减少负外部性。 当然,本文的测算还存在一些有待改进的方面。首先,受限于我国城市相关数据的可获得性,未能直接估算出各个城市的固定资产投资价格指数和经济折旧率,只是假定各城市固定资产投资价格指数和经济折旧率与其所在省份的数据相同,一定程度上缩小了城市之间的差异。其次,在推算城市能源消费总量时假定某城市的能源强度与该城市所属省份的能源强度相等,可能带来城市能源消耗总量估算的误差。另外,城市能源效率的产出指标只考虑了地区生产总值这一合意产出,未考虑废水、废气等非合意性产出。 参考文献: [1]IEA.WorldEnergyOutlook[M].Paris:InternationalEnergyAgency,2008:179-192. [2]MADLENERR,SUNAKY.ImpactsofUrbanizationonUrbanStructuresandEnergyDemand:WhatCanWeLearnforUrbanEnergyPlanningandUrbanizationManagement?[J].SustainableCitiesandSociety,2011,1(1):45-53. [3]NAKICENOVICN,JEFFERSONJM.GlobalEnergyPerspectivesto2050andBeyond[J].EnergyExplorationandExploitation,1996,14(2):149-151. [4]PATTERSONMG.WhatIsEnergyEfficiency?Concepts,IndicatorsandMethodologicalIssues[J].EnergyPolicy,1996,24(5):377-390. [5]BOSSEBOEUFD,CHATEAUB,LAPILLONNEB.Cross-countryComparisononEnergyEfficiencyIndicators:TheOn-goingEuropeanEfforttowardsaCommonMethodology[J].EnergyPolicy,1997,25(7):673-682. [6]HUJL,WANGSC.Total-factorEnergyEfficiencyofRegionsinChina[J].EnergyPolicy,2006,34(17):3206-3217. [7]WANGZH,FENGC,ZHANGB.AnEmpiricalAnalysisofChina’sEnergyEfficiencyfromBothStaticandDynamicPerspectives[J].Energy,2014(77):322-330. [8]ZHAY,ZHAOLL,BIANYW.MeasuringRegionalEfficiencyofEnergyandCarbonDioxideEmissionsinChina:AChanceConstrainedDEAApproach[J].Computers&OperationsResearch,2016(66):351-361. [9]杨红亮,史丹.能效研究方法和中国各地区能源效率的比较[J].经济理论与经济管理,2008(3):12-20. [10]李世祥,成金华.中国能源效率评价及其影响因素分析[J].统计研究,2008(10):18-25. [11]魏楚,沈满洪.能源效率与能源生产率:基于DEA方法的省际数据比较[J].数量经济技术经济研究,2007(9):110-121. [12]王强,樊杰,伍世代.1990-2009年中国区域能源效率时空分异特征与成因[J].地理研究,2014(1):43-56. [13]张志辉.中国区域能源效率演变及其影响因素[J].数量经济技术经济研究,2015(8):73-88. [14]ZHOUP,ANGBW,ZHOUDQ.MeasuringEconomy-wideEnergyEfficiencyPerformance:AParametricFrontierApproach[J].AppliedEnergy,2012,90(1):196-200. [15]赵金楼,李根,苏屹,等.我国能源效率地区差异及收敛性分析——基于随机前沿分析和面板单位根的实证研究[J].中国管理科学,2013(4):175-184. [16]林伯强,杜克锐.要素市场扭曲对能源效率的影响[J].经济研究,2013(9):125-136. [17]LINBQ,DUKR.MeasuringEnergyEfficiencyUnderHeterogeneousTechnologiesUsingALatentClassStochasticFrontierApproach:AnApplicationtoChineseEnergyEconomy[J].Energy,2014(76):884-890. [18]LINBQ,LONGHY.AStochasticFrontierAnalysisofEnergyEfficiencyofChina’sChemicalIndustry[J].JournalofCleanerProduction,2015(87):235-244. [19]DHAKALS.UrbanEnergyUseandCarbonEmissionsFromCitiesinChinaandPolicyImplications[J].EnergyPolicy,2009,37(1):4208-4219. [20]KEIRSTEADJ.BenchmarkingUrbanEnergyEfficiencyintheUK[J].EnergyPolicy,2013(63):575-587. [21]MACKRESE,JOHNSONK,DOWNSA,etal.The2013CityEnergyEfficiencyScorecard[R].Washington:AmericanCouncilforanEnergyEfficientEconomy(ACEEE),ReportNumberE13G,2013:1-245. [22]MAOJS,DUYC,CAIH,et.al.EnergyEfficienciesofIndustrialSectorsforChina’sMajorCities[J].ProcediaEnvironmentalSciences,2010(2):781-791. [23]张伟,吴文元.基于环境绩效的长三角都市圈全要素能源效率研究[J].经济研究,2011(10):95-109. [24]史红亮,杨先明.云南六大城市群全要素能源效率研究基于环境规制视角下的州市面板数据分析[J].昆明理工大学学报:社会科学版,2015(12):66-72. [25]李治,李国平.中国城市能源效率差异特征及影响因素分析[J].经济理论与经济管理,2010(7):17-23. [26]魏楚,沈满洪.能源效率及其影响因素:基于DEA的实证分析[J].管理世界,2007(8):66-76. [27]LEVINHM,JAMISONDT,RADNERR.ConceptsofEconomicEfficiencyandEducationalProduction[M]∥FROOMKINJT,JAMISONDT,RADNERR.EducationasAnIndustry,Princeton:NBER,1976:149-198. [28]SHEPHARDRW.TheoryofCostandProductionFunctions[M].Princeton:PrincetonUniversityPress,1970:3-26. [29]FARRELLMJ.TheMeasurementofProductionEfficiency[J].JournalofRoyalStatisticalSociety(SeriesA),1957,120(3):253-281. [30]陶长琪,王志平.随机前沿方法的研究进展与展望[J].数量经济技术经济研究,2011(11):148-161. [31]王益煊,吴优.中国国有经济固定资本存量初步测算[J].统计研究,2003(5):40-45. [32]孙琳琳,任若恩.中国资本投入和全要素生产率的估算[J].世界经济,2005(12):3-13. [33]钱雪亚,王秋实,伊立夫.中国人力资本和物质资本存量:基于总资本框架的估算[J].商业经济与管理,2009(3):39-45. [34]张军,吴桂英,张吉鹏.中国省际物质资本存量估算:1952-2000[J].经济研究,2004(10):35-44. [35]单豪杰.中国资本存量K的再估算:1952-2006年[J].数量经济技术经济研究,2008(10):17-31. [36]GOLDSMITHRW.APerpetualInventoryofNationalWealth[M]∥GAINSBURGHMR.StudiesinIncomeandWealth(Vol.14),Princeton:NBER,1951:5-73. [37]万东华.一种新的经济折旧率测算方法及其应用[J].统计研究,2009(10):15-18. [38]肖红叶,郝枫.资本永续盘存法及其国内应用[J].财贸经济,2005(3):55-62. [39]徐杰,段万春,杨建龙.中国资本存量的重估[J].统计研究,2010(12):72-77. [40]叶裕民.全国及各省区市全要素生产率的计算和分析[J].经济学家,2002(3):115-121. [41]CHOWGC.CapitalFormationandEconomicGrowthinChina[J].QuarterlyJournalofEconomics,1993,108(3):809-842. [42]柯善咨,向娟.1996-2009年中国城市固定资本存量估算[J].统计研究,2012(7):19-24. [43]REINSDORFM,COVERM.MeasurementofCapitalStocks,ConsumptionofFixedCapital,andCapitalServices[R].ReportonaPresentationtotheCentralAmericanAdHocGrouponNationalAccounts,DominicanRepublic:SantoDomingo,July12,2005:1-6. (责任编辑孙敬水) 收稿日期:2016-04-28 基金项目:国家自然科学基金面上项目(71373240);教育部人文社科规划基金项目(13YJA630012);教育部人文社科重点研究基地浙江工商大学现代商贸研究中心和浙江省2011协同创新中心——现代商贸流通体系建设协同创新中心项目(15SMGK032);浙江省“之江青年课题研究”项目(13ZJQN005YB);浙江省高校人文社科重点研究基地(统计学)项目(1020XJ3314044G) 作者简介:陈龙,男,博士研究生,主要从事经济统计研究;李金昌,男,教授,博士,博士生导师,主要从事统计理论与方法、抽样技术等研究;程开明,男,教授,博士,博士生导师,主要从事城市与区域经济、空间统计方法及应用研究,通讯作者。 中图分类号:C812 文献标识码:A 文章编号:1000-2154(2016)07-0083-14 Measurement and Analysis of Urban Energy Efficiency in China CHEN Long1, LI Jin-chang2, CHENG Kai-ming1 (1.SchoolofStatisticsandMathematics,ZhejiangGongshangUniversity,Hangzhou310018,China;2.SchoolofDataSciences,ZhejiangUniversityofFinance&Economics,Hangzhou310018,China) Abstract:With the rapid development of urbanization in China, energy consumption is rising increasingly. Urban energy consumption accounts for the biggest proportion of total energy consumption. It is important to measure urban energy efficiency scientifically and accurately for reasonable energy policy making. From multiple channels, data are collected and carefully prepared. Then the perpetual inventory method is adopted to measure the urban capital stock. According to Zhou et al.(2012)’s definition of energy efficiency based on Shephard energy distance function, the inefficiency of capital and labor is decomposed from the total production function. Based on urban capital stock, SFA is applied to measure the total factor energy efficiency of China’s 245 cities from 2001 to 2013. Then urban total factor energy efficiency is compared among four regions, northern cities and southern cities, and city scales. Results show that the average of urban energy efficiency is slightly higher than 0.6, the top 10 cities are mainly located in the eastern coastal region; the last 10 cities are mainly located in the western region. Urban energy efficiency among four regions, northern and southern cities, and five scales shows obvious differences. Overall, there is a great potentiality in energy-saving for China’s cities in the future. Key words:urban capital stock; stochastic frontier analysis; perpetual inventory method; urban total factor energy efficiency