地震诱发滑坡风险概率模型及其应用

李凯平　石　崇　王如宾　蔡征龙

(1．河海大学 岩土力学与堤坝工程教育部重点实验室， 南京　210098； 2．河海大学 岩土工程科学研究所， 南京　210098)



地震诱发滑坡风险概率模型及其应用

李凯平1，2石崇1，2王如宾1，2蔡征龙1，2

(1．河海大学 岩土力学与堤坝工程教育部重点实验室， 南京210098； 2．河海大学 岩土工程科学研究所， 南京210098)

摘要：边坡在地震作用下的滑坡概率是工程师非常关注的问题．针对该问题，利用简化Bishop法，考虑岩土体参数不确定性和随机地震发生概率，建立了两种随机性耦合的全概率分析方法．该方法首先采用边坡可靠度理论计算边坡的失效概率．其次，通过地震烈度的极值Ⅲ型概率分布求解随机地震发生概率．最终通过Matlab软件进行程序实现，可估计多种条件下边坡的滑坡概率．典型模型验证结果表明，该方法有一定的合理性．

关键词：地震；滑坡概率；全概率；简化Bishop法

0引言

在矿山、水利水电、公路以及铁路等领域存在大量的边坡工程．而滑坡是自然界和岩土工程中最常见的地质灾害，往往给人类的生命和财产造成频繁而巨大的损失．在诱发滑坡的众多因素中地震是其中一个重要因素，研究边坡在地震作用下的滑坡概率具有非常重要的意义．

目前地震工况下边坡稳定性已经存在大量的研究，但这些方法大多数是基于确定性岩土体参数或确定性地震烈度进行计算，或者为考虑参数随机的边坡稳定性方法．贾伟[1]在基于确定性地震和降雨工况因素下，在定量分析基础上，考虑了岩土体参数对边坡稳定的影响，从非确定性分析的角度进行了边坡稳定的可靠度指标的计算以及岩土体参数对边坡稳定的敏感性分析；李元雄[2]在不考虑坡面形态和岩土体参数的影响下，基于蒙特卡罗法，并结合稳定性计算的剩余推力法和Sarma法，研究了随机地震作用下边坡的可靠性．在边坡地震稳定概率分析中，闫俊维，王曙光等[3]基于可靠度原理，结合最优化方法和传递系数法来求解边坡可靠度指标最小值的优化问题；陈菊香，卓建平等[4]基于Morgenstern-Price条分法和Monte-Carlo数值模拟法，将地震系数视为随机变量，运用可靠度理论分析了地震系数的分布特征对土坡稳定性的影响和最危险滑面的变化规律．

在此基础上，本文利用简化Bishop法，考虑岩土体参数不确定性和随机地震发生概率，建立两种随机性耦合的全概率方法．首先，采用边坡可靠度理论，将响应面法和验算点法相结合来计算边坡的失效概率．其次，通过地震烈度的极值Ⅲ型概率分布求解随机地震发生概率，并采用Matlab软件进行程序实现．

1地震滑坡失效概率分析

地震是诱发滑坡体的显著变形及失稳的主要因素[5-6]．通过分析区域内地震发生概率，以及此地震作用下滑坡发生的可能性，即将诱发因素的概率值与滑坡稳定性求解过程结合，以达到完整意义上的滑坡稳定性的失效概率计算．

若假设地震烈度指标为A，滑坡事件为B，地震条件下滑坡的发生为条件概率计算．即：

(1)

式中，P(AB)为地震与滑坡事件同时出现的概率，即A和B的联合概率；P(A)为地震烈度发生的概率；P(B|A)为施加一定地震惯性力在滑坡体上，考虑岩土体强度参数的随机分布，计算滑坡的失效概率．

1.1滑坡失效概率计算模型

由于边坡系统是一个复杂的体系，随机变量之间的关系表现为高度非线性且通常不易于用显式表达．因此采用响应面法和验算点法相结合来进行边坡体系的可靠度分析[7-9]．其基本思想是：1)将已选定的随机变量(c和tanφ)进行处理，若随机变量的分布形式为正态分布则不需进行正态化，若随机变量的分布形式为非正态分布，则需先将其进行当量正态化；2)利用响应面法求得近似响应面函数，再利用求得的响应面函数和验算点法求得边坡体系的失效概率．

对于考虑n个随机变量x1，x2，…，xn的情况，响应面法解析式的形式通常取不含交叉项的二次多项式[10]，即：

(2)

式中，A，Bi和Ci(i=1，2，…，n)均为待定系数，总计2n+1个待定系数．

运用响应面法重构一个解析表达式来近似求其极限状态曲面，其重构方法的步骤可归纳为：

3)利用式(2)和步骤(2)求得2n+1个函数值，解出待定系数A，Bi，Ci(i=1，2，…，n)，得到二次多项式近似的功能函数，从而确定边坡的极限状态方程；

4)利用验算点法求解可靠度指标β(k)和相应的迭代点x*(k)，其中上标k表示第k步迭代；

5)判断收敛条件，即：|β(k)-β(k-1)|<ε是否满足(ε为可靠度指标的误差限)．若不满足误差要求，则按下式求得到新的展开点以代替X(0)．然后重复步骤2)～4)，直至满足上述收敛条件．

(3)

利用响应面法和验算点法求解出边坡可靠度β后，即可利用公式Pf=1-Φ(β)求出滑坡的失效概率．

1.2函数响应确定

1.2.1基于简化Bishop法的边坡极限状态方程

在利用响应面法进行滑坡失效概率计算时，用到的函数响应即为安全系数．这里采用简化Bishop法来求解边坡安全系数，简化Bishop法[11]是边坡稳定分析极限平衡法的一种，它假定滑动面为圆弧面，考虑了土条侧面的作用力．对于圆弧滑动面，大量实际边坡稳定分析计算表明，简化Bishop法计算结果与满足所有平衡条件的严格的极限平衡法的计算结果近乎一致，但是简化Bishop的计算过程要比严格的极限平衡法简单得多．

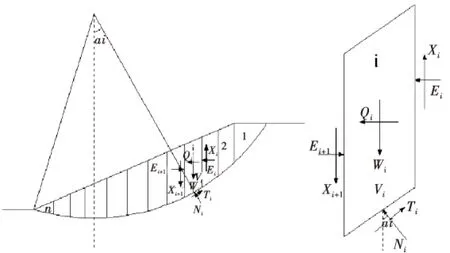
图1　简化Bishop法受力分析图

简化Bishop法的安全系数Fs的计算公式为：

(4)

式中，Wi为土条自重；ci和φi分别为土条的粘聚力和内摩擦角；bi为土条的宽度；R为滑动圆弧的半径；Qi为作用在土条重心处的水平向地震惯性力，方向指向坡外[12]；Vi为作用在土条重心处的竖向地震惯性力，方向竖直向下；MQi为水平向地震惯性力Qi对滑动圆心的矩．

边坡的功能函数为：

(5)

相应的极限状态方程为：

(6)

在大量的土性参数中，抗剪强度参数和重度会较大程度地影响边坡的稳定性，而容重的变异性相对于抗剪强度参数粘聚力和内摩擦角较小．因此在考虑不确定性因素时，主要考虑抗剪强度参数的影响，故在进行边坡可靠度分析计算时，选取的随机变量主要是粘聚力和内摩擦角，并考虑土性参数变异性的影响．

1.2.2简化Bishop法积分表达式

简化Bishop法在边坡安全系数的迭代计算过程中需要对每一条块求和，计算比较复杂．而且求解时初值选得不好可能会导致求出的解不收敛．采用积分法[13-14]替代条分法计算边坡安全系数，不仅可以简化计算，还可以提高计算精度．

图2　边坡稳定分析坐标系及微分土条作用力分析

坡面ED为单一直线斜坡，坡高为h，坡度为i=1∶m，岩土体参数均已知，原点取在坡脚处．如图2所示．

边坡的边界方程为：

(7)

滑动圆弧方程为：

(8)

经过推导计算可得：

(9)

式中：ma=cosα+sinαtanφ/Fs.

2地震诱发因素的概率计算

地震作用是一个随机发生的过程，并且各种烈度等级的地震都是有可能发生的，因此分析在确定性地震荷载作用下某一边坡稳定性是不完整的．所以在对边坡的稳定性进行分析时，还要考虑边坡遭受随机地震荷载等不确定因素．

用地震危险性分析方法得到的某场地不同超越概率水平的地震烈度值，是确定地震作用概率分布的基本数据．地震烈度的概率分布主要有极值Ⅰ型，极值Ⅱ型和极值Ⅲ型分布[15]．这3种概率分布的差别主要在于原分布尾部的变化规律．如果原分布的尾部是指数型，则最大值收敛于极值Ⅰ型；如果原分布的尾部是多项式形式，则最大值分布趋向于极值Ⅱ型；如果原分布的尾部有界，则最大值分布趋向于极值Ⅲ型．因为地震震级和烈度均存在上界，所以认为极值Ⅲ型分布更符合地震烈度概率分布的实际情况．

极大值的极值Ⅲ型分布可表达为：

(10)

式中，ω为地震烈度的上限值，取12度；ε为众值烈度，取超越概率为63%的地震烈度为众值烈度；K为形状参数，其值采用分位值法计算确定，具体计算时采用50年内与超越概率为10%的烈度相对应的K值．

已知T年内地震烈度的概率分布为极值Ⅲ型，则在任意t年内的概率分布为：

(11)

则地震烈度的发生概率可用下式计算：

(12)

3算例应用分析

3.1计算模型及参数

本次计算实例采用1987年由澳大利亚计算机应用协会(ACADS)委托Monash大学B.Donald教授和P.Giam博士给出的用来调查澳大利亚本土范围内边坡所用到的分析边坡稳定性程序的考核题．所涉及边坡是一个非均匀介质边坡，该坡体分为3个不同的土层，其几何尺寸如图3所示，材料参数取值参考见表1，地震烈度的概率分布服从极值Ⅲ型分布且坡址处50年不同超越概率水平的地震烈度值见表2，分别考虑水平地震系数为0.05、0.10和0.20三种情形(即考虑地震烈度为6度、7度和8度3种情形)．各发生地震烈度对应的最危险滑面形状如图4所示．

图3　算例边坡几何尺寸

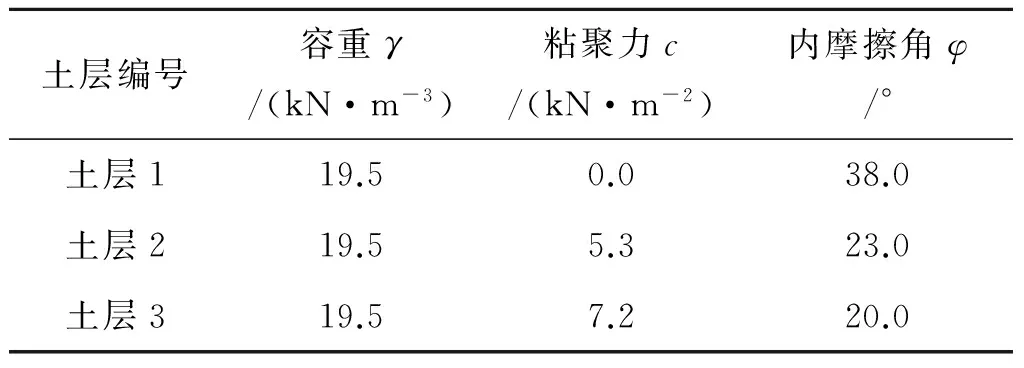
土层编号容重γ/(kN·m-3)粘聚力c/(kN·m-2)内摩擦角φ/°土层119.50.038.0土层219.55.323.0土层319.57.220.0

表2　坡址50年不同超越概率水平的地震烈度值

图4　各发生地震烈度对应的最危险滑面形状

岩土力学参数具有变异性，不同性质的材料的变异系数也会有所差异．考虑岩土不同随机变量的变异系数的取值范围，对于本文采用的非均质算例，所有土类的粘聚力的变异系数范围是20%～50%，内摩擦角的正切值的变异系数范围为5%～15%．不妨取粘聚力的变异系数δc均为0.4，内摩擦角的正切的变异系数δtanφ均为0.1．计算分析就粘聚力和内摩擦角正切值服从正态分布及对数正态分布以及两者在不同的分布组合情况下的可靠度进行计算分析．

3.2不考虑地震概率的边坡失效概率P(B|A)的计算

利用Matlab编制将响应面法和验算点法相结合求解边坡可靠度的程序，考虑：1)粘聚力和内摩擦角正切均服从正态分布；2)粘聚力服从正态分布，内摩擦角正切服从对数正态分布；3)粘聚力服从对数正态分布，内摩擦角正切服从正态分布；4)粘聚力和内摩擦角正切均服从对数正态分布4种情形，并利用公式Pf=1-Φ(β)即可求解出不考虑地震概率的边坡失效概率P(B|A)．其计算结果见图5及表3．

图5　不考虑地震概率的不同水平地震系数下边坡失效概率P(B|A)

参数分布类型水平地震系数安全系数可靠度P(B|A)/%粘聚力和内摩擦角正切均服从正态分布0.051.2502.4280.760.11.1221.3638.60.20.935-0.72176.5粘聚力服从正态分布,内摩擦角正切服从对数正态分布0.051.2412.3420.950.11.1141.3468.920.20.928-0.78978.52粘聚力服从对数正态分布,内摩擦角正切服从正态分布0.051.2382.2951.10.11.1101.22211.080.20.925-0.87080.78粘聚力和内摩擦角正切均服从对数正态分布0.051.2332.1591.580.11.1061.09313.790.20.922-0.98883.80

从以上结果可以看出：土性参数粘聚力和内摩擦角正切同取正态分布比同取对数正态分布的失效概率要略小，且粘聚力和内摩擦角正切分别取不同分布时，其失效概率介于两者之间．

3.3地震发生概率P(A)的计算

本算例地震烈度的上限ω取12度．取设计基准期为50年，超越概率为10%的烈度相当于地震烈度区划图规定的基本烈度，即Ib取7.5度，超越概率为63%的地震烈度为众值烈度，即ε取6.2度．采用分位值法求得基本烈度对应的形状系数 为8.8674．

取I为6度，将各参数代入地震烈度的概率分布函数中，求得：

(13)

取I为7度，将各参数代入地震烈度的概率分布函数中，求得：

(14)

从而可以求得在50年设计基准期内，地震烈度I=6度发生的概率为：

(15)

同理，可求出在50年设计基准期内，地震烈度为7、8度发生的概率，具体结果见表4．

表4　各级地震烈度发生概率

3.4考虑地震概率的边坡失效概率P(AB)的计算

利用公式P(AB)=P(A)P(B|A)，结合4.2和4.3节计算出的P(B|A)和P(A)，便可算出考虑地震概率的不同水平地震系数下边坡失效概率P(AB)．其详细计算结果见表5和图6．

表5　算例边坡失效概率计算结果汇总

图6　考虑地震概率的不同水平地震系数下边坡失效概率P(AB)

4结论

本文结合响应面法和简化Bishop法，同时考虑地震发生概率，通过全概率公式建立地震作用下的滑坡概率模型．得到主要结论如下：

1) 建立地震诱发滑坡的风险概率模型，应该通过建立全概率公式综合考虑岩土体参数的不确定性和地震随机性的影响．

2)对于一般边坡的圆弧滑动面，采用积分法替代条分法计算边坡安全系数，不仅有效地避免了条分法中土条数目划分不同所带来的计算误差，而且大大提高了计算效率．

3)针对边坡在地震作用下的滑坡概率问题，结合简化Bishop法和可靠度原理中的响应面法和验算点法，并考虑岩土体参数的变异性，编制了计算边坡可靠度指标的Matlab程序，从而快速有效地计算出边坡的失效概率．

参考文献：

[1]贾伟．基于极限平衡法和强度折减法的边坡稳定性分析[J]．云南冶金，2014，43(4)：1-6．

[2]李元雄．随机地震作用下滑坡稳定性可靠度分析[J]．煤田地质与勘探，2010，38(3)：51-54．

[3]闫俊维，王曙光，陈静瑜．基于最优化方法的边坡稳定可靠度计算分析[J]．西部交通科技，2015，(3)：18-22．

[4]陈菊香，卓建平，卢坤林．考虑地震随机性的土坡可靠度分析[J]．水电能源科学，2010，28(2)：92-94．

[5]张铎，吴中海，李家存，等．国内外地震滑坡研究综述[J]．地质力学学报，2013，19(3)：225-241．

[6]李为乐，伍霁，吕宝雄．地震滑坡研究回顾与展望[J]．灾害学，2011，26(3)：103-108．

[7]李典庆，周创兵，陈益峰，等．边坡可靠度分析的随机响应面法及程序实现[J]．岩石力学与工程学报，2010，29(8)：1513-1523．

[8]苏永华，赵明华，蒋德松，等．响应面方法在边坡稳定可靠度分析中的应用[J]．岩石力学与工程学报，2006，25(7)：1417-1424．

[9]许英，姜华峰，马国山．基于响应面法的边坡稳定可靠性分析[J]．水运工程，2009(11)．

[10] 张璐璐．岩土工程可靠度理论[M]．上海：同济大学出版社，2011．

[11] 殷宗泽．土工原理[M]．北京：中国水利水电出版社，2007．

[12] NB35047-2015．水电工程水工建筑物抗震设计规范[S]．

[13] 蔡征龙，孟永东，苏情明，等．基于Matlab的土坡稳定分析的解析计算[J]．三峡大学学报：自然科学版，2014，36(5)：60-63．

[14] 蒋斌松，康伟．边坡稳定性中BISHOP法的解析计算[J]．中国矿业大学学报，2008，37(3)：287-290．

[15] 陈珊桦，张有明，尤宇星，等．极值理论在福建沿海地区地震预测中的研究与应用[J]．华北地震科学，2013，31(3)：29-34．

[责任编辑王康平]

DOI：10.13393/j.cnki.issn.1672-948X.2016.03.006

收稿日期：2016-01-25

基金项目：“十二五”国家科技支撑计划(2013BAB06B01)；江苏省基础研究计划(自然科学基金)(BK20130846)

通信作者：李凯平(1992-)，男，硕士研究生，主要从事岩石高边坡方面的研究工作．E-mail：lkp1140661425@163.com

中图分类号：TU435

文献标识码：A

文章编号：1672-948X(2016)03-0023-05

Risk Probability Models of Earthquake-induced Landslides and Its Application

Li Kaiping1,2Shi Chong1,2Wang Rubin1,2Cai Zhenglong1,2

(1. Key Laboratory of Ministry of Education for Geomechanics & Embankment Engineering, Hohai Univ., Nanjing 210098, China; 2. Geotechnical Research Institute, Hohai Univ., Nanjing 210098, China)

AbstractLandslide probability of slope under earthquake is a matter of great concern to engineers. To solve the problem, by using simplified Bishop method, considering the uncertainty of soil parameters and the probability of random earthquake, a total probability analysis method is established for two kinds of random coupling. Firstly, the failure probability of the slope is calculated by the slope reliability theory. Secondly, the probability of random earthquake occurrence is solved by the extreme Ⅲ probabilistic seismic intensity distribution. Finally, the program is realized through Matlab software and the landslide probability can be estimated under a variety of conditions. Typical model validation results show that the method has a certain rationality.

Keywordsearthquake;landslide probability;total probability;simplified Bishop method