无轴承外转子异步电机转子导条对转矩及悬浮力的性能影响*

孙宇新，　王　浩

(江苏大学 电气信息工程学院，江苏 镇江　212013)



无轴承外转子异步电机转子导条对转矩及悬浮力的性能影响*

孙宇新，王浩

(江苏大学 电气信息工程学院，江苏 镇江212013)

摘要：在介绍了无轴承异步电机工作原理及径向力产生原理和转矩产生原理的基础上，推导了无轴承外转子异步电机数学模型。利用有限元方法分析了无轴承外转子异步电机的磁场，给出了磁场分布图，通过有限元软件模块参数化的功能对样机转子导条数及转子槽尺寸进行了分析。研究表明，转矩脉动及悬浮力脉动受转子导条数的影响较大，转子槽尺寸与平均转矩及平均悬浮力的关系受电机磁饱和的影响。

关键词：无轴承电机； 转子导条； 有限元； 感应电机； 模型； 外转子

0引言

随着科学技术的发展，大功率高速电机广泛应用于高速机床电主轴、涡轮分子泵、高速离心机、压缩机、飞轮储能等工业生产领域。与普通的中、低速电机相比，高速电机具有十分明显的优点： 体积小、重量轻、功率密度高；电机转动惯量小、动态响应快；可以直接驱动高速负载，降低系统噪声，提高系统效率。高速电机由于需要机械轴承来支承，在运动过程中存在很严重的机械摩擦与磨损问题，不仅降低了电机工作效率，同时也大大缩短了电机和轴承的使用寿命。机械轴承需润滑和维护，在一些特殊的应用领域，如真空、超洁净环境中，润滑油无法使用，使机械轴承的维护更是成为一大难题。为了解决机械轴承的这些问题，国外学者提出了磁悬浮轴承(简称磁轴承)。磁轴承是利用电磁力将转子悬浮于空间，实现转子之间无机械接触的一种新型高性能轴承，从根本上改变了传统的高速电机转子支撑形式。磁轴承具有无机械摩擦、无磨损、无需润滑和密封、寿命长等诸多突出优点。传统的磁轴承电机体积通常比较庞大、成本较高，且需要大量的连接导线及单相逆变器，大大限制了其发展和应用[1]。

为了克服磁轴承电机的缺陷并充分利用磁轴承的诸多优点，国外学者提出了一种集自悬浮与旋转功能为一体的新型磁悬浮电机(称为无轴承电机)。无轴承电机是电机和磁轴承研究领域的重大创新，从根本上改变了传统电机的结构和控制。利用磁轴承和电机定子结构的相似性，把磁轴承中的悬浮绕组叠绕在电机定子绕组上，使两种磁场合成一体，且能同时独立控制电机转子的悬浮和旋转。除具有磁轴承电机的所有优点之外，无轴承电机还具有如下突出的优点： 电机尺寸小、功率密度高、电机轴向长度较短、易于向更高转速和更大功率方向发展。因此，无轴承电机的研究受到了各国电力传动界的高度重视。

近年来国内外提出了各种各样的无轴承电机，如无轴承异步电机[2]、无轴承永磁电机[3]、超导轴承电机[4]和无轴承开关磁阻发电机[5]等。无轴承电机技术的发展给难以实现的高速高精电气传动问题以及特殊环境的传动问题提供了解决方案。它的成熟与发展对特种电力传动装备产生重大的技术进步和变革，在高速精密机械加工、航空航大、生命科学、超高速飞轮储能等领域已经显出了极其重要的科研与应用价值，尤其是无轴承电机无接触和无需润滑的特点，也特别适合于纯净洁室、无菌车间、真空技术、腐蚀性介质的传输等特殊场合。

无轴承异步电动机具有结构简单、成本低、可靠性高、更容易实现弱磁控制等优点。无轴承异步电机可使用无位置检测的开环操作，大大降低了控制系统的成本。文献[6]分析了无轴承异步电机转子倾斜时产生轴向振荡的原因，并提出了一种具有两串联转子结构的无轴承异步电机来消除轴向力。文献[7]提出了一种带分裂绕组的无轴承异步电机，采用各相独立控制的方法来改善电机的容错性能。文献[8]分析了无轴承异步电机径向力变化规律，得出如何有效获得最大悬浮力的方法，并分析了磁饱和对悬浮力的影响。

本文提出一种适用于飞轮储能系统的无轴承外转子异步电机，并详细说明了无轴承异步电机的基本原理，推导了该电机径向悬浮力的数学模型。同时采用有限元软件分析了该电机的磁场分布情况，对电机转子导条数及其尺寸进行了优化设计，得到了转子导条数及尺寸对电机转矩及悬浮力的影响规律。

1无轴承外转子异步电机工作原理

无轴承外转子异步电机是在普通外转子异步电机的定子槽中加入一套悬浮控制绕组，利用悬浮控制绕组产生的磁场来改变气隙中合成磁场的分布，从而产生径向悬浮力来实现转轴的稳定悬浮。图1为无轴承外转子异步电机结构图。两套三相绕组叠绕在同一个定子槽内，其中内层绕组为四极绕组称为转矩绕组，用来产生电机转矩，外层绕组为二极绕组用来控制转子的径向位置，称为悬浮绕组。其中转矩绕组和悬浮绕组每相串联的有效匝数分别为Wt、Ws。在转矩绕组和悬浮绕组中分别通入电流It、Is，则分别产生四极磁链ψt和两极磁链ψs。

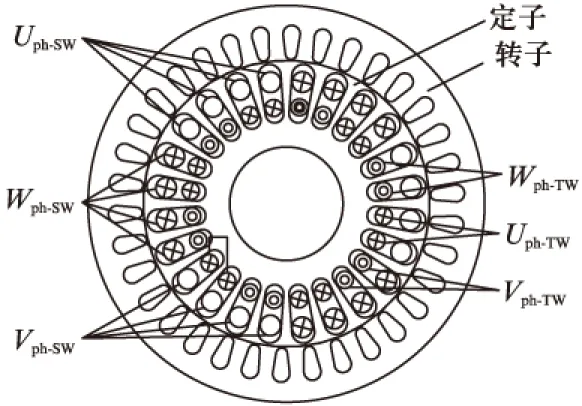
图1　无轴承外转子异步电机模型

对于无轴承异步电机来说，其径向力的产生主要源于垂直于电机转子表面的麦克斯韦力。普通异步电机中的磁场呈对称分布，其麦克斯韦力合力为零。当转子发生偏心时，磁场的对称性将会被破坏，进而导致麦克斯韦合力不为零，且其作用方向和转子偏心的方向一致，指向气隙最小处，该力即为不平衡磁拉力。为实现转子的稳定悬浮，无轴承异步电机在绕制有(极对数为Pt)转矩绕组的异步电机定子上再叠绕悬浮绕组(极对数为Ps=Pt±1)，通过控制悬浮绕组中的电流打破电机旋转磁场的平衡，进而产生与不平衡磁拉力方向相反的悬浮力，使转子回到电机中心位置。图2所示为无轴承异步电机悬浮力产生原理图。如图2(a)所示，受到二极悬浮绕组磁场的影响，A区域磁通增强而其对称的B区域磁通减弱，进而产生X轴正方向的悬浮力；图2(b)中，在四极转矩绕组磁场Ψt和二极悬浮绕组磁场Ψs的共同作用下，A区域磁通大于B区域磁通，从而产生Y轴正方向的悬浮力[9]。

图2　径向悬浮力产生原理

2无轴承外转子异步电机数学模型

2.1悬浮力数学模型

设电机中的气隙磁密为B，则作用在转子外表面单位面积上的麦克斯韦力为

(1)

其沿X、Y方向上的分量为

(2)

(3)

式中：μ0——气隙磁导率；

l——电机铁心长度；

r——转子内半径。

由于电机中的气隙磁密是由转矩控制绕组和径向控制绕组共同产生的合成气隙磁密，即

B(φ)=Btcos(Ptφ-μ)+Bscos(Psφ-λ)

(4)

式中：λ、μ——悬浮绕组和转矩绕组的初始磁场相位角。

将式(4)代入式(2)、式(3)，并分别积分运算。则当Ps=Pt-1时，可得

FX=FMcos(λ-μ)

FY=-FMsin(λ-μ)

(5)

其中

(6)

每极气隙磁通为

(7)

每相气隙磁链为

(8)

三相绕组合成气隙磁链的空间向量幅值为

(9)

将式(7)～式(9)代入式(6)可得

(10)

2.2电机旋转部分数学模型

无轴承异步电机转矩产生原理和普通异步电机相似，即转矩绕组电流产生的旋转磁场在转子导条中产生感应电流，进而得到转子磁场，定子磁场和转子磁场相互作用产生转矩；而悬浮绕组电流产生的Ps对极旋转磁场也会在转子上感应出电流并得到Ps对极的转子磁场，两个磁场的相互作用同样也会产生转矩。此时，笼式无轴承外转子异步电机可以看成两个极对数分别为Pt、Ps的电机，其总转矩为两个电机转矩相加而成。但通常悬浮绕组电流产生的转矩较小，可以忽略不计。由此得到电机的转矩方程可近似表示为

Te=Pt(istqψtd-istdψtq)

(11)

式中：istd、istq——转矩绕组电流在d、q轴上的电流分量；

ψtd、ψtq——转矩绕组产生的气隙磁链在d、q轴上的气隙磁链分量。

3电机模型

文中的研究对象为一台功率为0.5kW的无轴承外转子异步电机。表1为所选无轴承外转子异步电机主要参数。

无轴承外转子异步电机的磁场分布复杂，悬浮力与绕组电流之间存在复杂的非线性关系，通常的磁路分析法难以准确计算和分析，利用有限元法克服磁路分析方法的不足，并使抽象的磁场分布更加清晰。

根据表1，采用有限元分析软件建立电机的二维分析模型如图3所示。定子槽分为内层和外层2部分，分别嵌入转矩绕组和悬浮绕组，将2套绕组同时通以三相对称电流。

表1　无轴承外转子异步电机参数

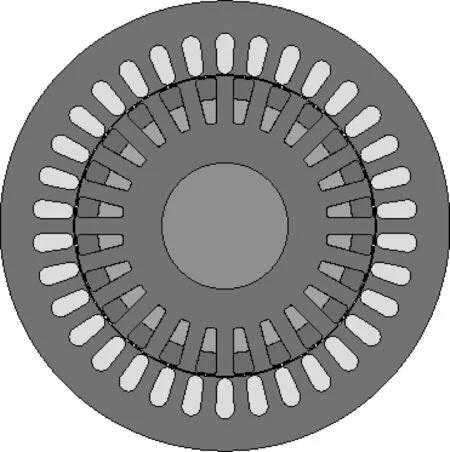
图3　电机端面模型

4转矩及悬浮力特性分析

通过单一变量的分析方法，本文计算并绘制出径向悬浮力与转子导条数、转子槽尺寸等物理量之间的关系曲线。假设转子始终受到沿X轴正方向的径向悬浮力作用，且转子一直处于定子中心。图4为无轴承外转子电机截面图。在图4中为实现电机在获得最大输出转矩和最大悬浮力的基础上同时获得最小的转矩脉动和悬浮力脉动，对转子槽的数目及尺寸进行了优化分析。

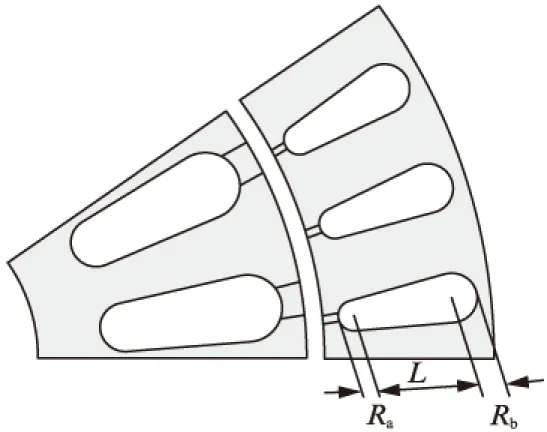
图4　无轴承外转子电机截面图

4.1转子导条数对转矩及悬浮力的影响

笼型转子感应电机在选取转子槽数时，必须与定子槽数有恰当的配合，即槽配比。若配合不当，会使电机性能恶化，可能导致附加损耗、附加转矩、振动与噪声增加，从而使效率降低、温升增高、起动性能变坏、甚至无法起动。本文主要研究转子导条数对电机转矩和悬浮力的影响[10]。

从式(10)可知，平均悬浮力与转矩及悬浮绕组的三相合成气隙磁链有关，而随着导条数目的增加，转子感应电动势会随之增大，从而造成气隙磁密的增加，由此引起气隙磁通的变化。通过式(7)～式(9)可知，三相合成气隙磁链会随着导条数目的变化而变化。图5为悬浮力与转子导条数的关系图。从图5可以看出平均悬浮力随着导条数的增大而增大。同时悬浮力脉动随着导条数的增大而减小，并在导条数为34时达到最小值10.49%。图6为转矩与转子导条数的关系图。从图6可以看出，随着转子导条数的增加，平均转矩基本不变，而转矩脉动影响较大。在导条数为偶数时转矩脉动明显大于导条数为奇数时的转矩脉动。

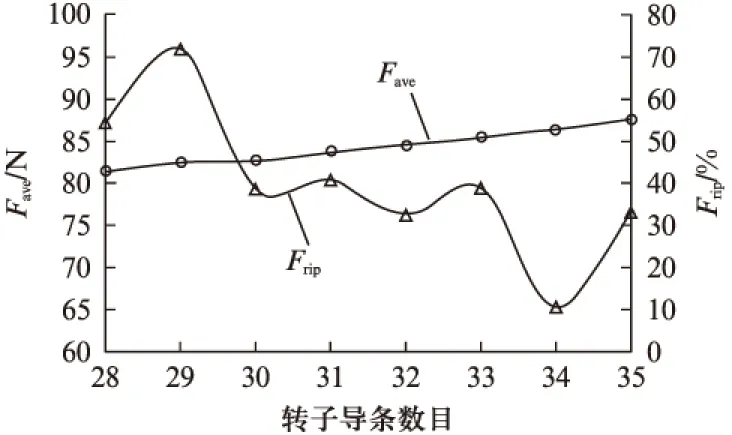
图5　平均悬浮力、悬浮力脉动与导条数的关系

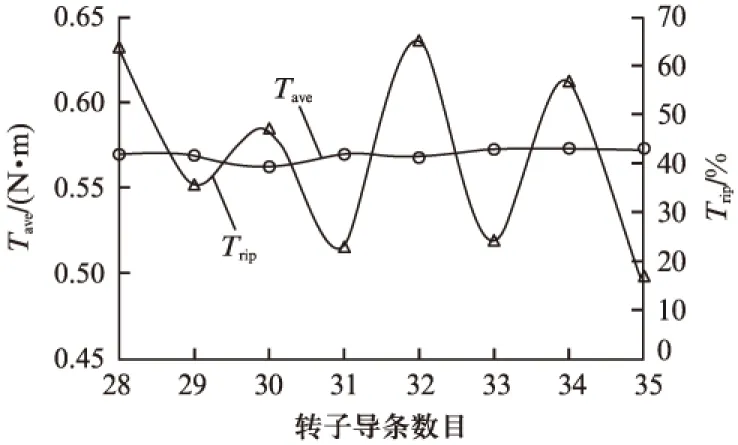
图6　平均转矩、转矩脉动与导条数目的关系

4.2转子槽尺寸对转矩及悬浮力的影响

根据感应电机的工作原理，当对称三相电流供给到定子绕组时，旋转磁场将切割转子导体产生感应电动势和电流，转子载流导体和磁场相对作用才产生转矩。应当指出的是，转子槽形尺寸是影响感应电流及感应电动机的重要因素，如电机起动电流、起动转矩、效率、温度、功率因数等性能。所以，优化转子槽形尺寸以满足转矩和悬浮力的设计要求非常重要。一般的电机设计都是以电磁设计方法来确定转子槽尺寸，本文在结合有限元软件参数模块化的基础上对转矩及悬浮力特性进行了分析。

从图7可知，随着Ra的增加，转矩基本呈现单调递增的趋势。随着L的增加，转矩呈现先增加后减小的趋势。以Ra=2mm为例(其中Rb=Ra+0.4mm)，当L增加时，由于转子轭部铁心磁密未饱和，转矩缓缓增加，并在L=6mm 时，转矩取得最大值0.777N·m。此时，转子轭部铁心磁密趋于饱和，所以当L继续增加时，转矩反而开始减小。由此得到结论： 当转子槽尺寸满足Ra=2-0.1n，L=6+0.2n，(n为整数)时，转矩取得最大值。图8可以看出悬浮力随着Ra和L的增加呈现一个急剧减小的趋势，及转子尺寸的增加对绕组三相合成气隙磁链有减小作用。

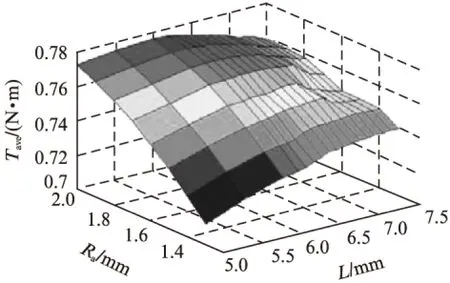
图7　平均转矩与转子槽尺寸的关系

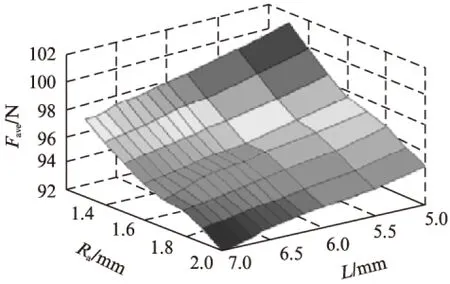
图8　平均悬浮力与转子槽尺寸的关系

5结语

文中阐述了无轴承外转子异步电机工作原理，并推导了电机数学模型，通过有限元软件模块参数化的功能对电机转子导条数及转子槽尺寸进行了分析。得出以下结论： 增加转子导条数在增加平均悬浮力的同时减小悬浮力脉动；转子导条数对转矩脉动的影响也很大，转子导条数为偶数时的转矩脉动明显大于奇数条件下的转矩脉动。在忽略电机磁饱和的情况下，平均转矩随着转子槽尺寸的增加而增加，然而悬浮力随着转子槽尺寸的增加而减小。这为设计性能优良的无轴承外转子异步电机提供依据。

【参 考 文 献】

[1]SCHUHMANN T, HOFMANN W, WERNER R. Improving operational performance of active magnetic bearings using Kalman filter and state feedback control [J]. IEEE Trans Ind Electron, 2012,59(2)： 821-829.

[2]CHIBA A, FUKAO T, RAHMAN M. Vibration suppression of a flexible shaft with a simplified bearingless induction motor drive [J]. IEEE Trans Ind Appl, 2008,44(3)： 745-752.

[3]REICHERT T, KOLAR J W, NUSSBAUMER T. Stator tooth design study for bearingless exterior rotor PMSM [J]. IEEE Trans Ind Appl, 2013,49(4)： 1516-1521.

[4]LI WL, CHAU K T, CHING T W, et al. Design of a high-speed superconducting bearingless machine for flywheel energy storage systems [J]. IEEE Trans Appl Supercond, 2015,25(3)： 5700204.

[5]CAO X, DENG ZQ. A full-period generating mode for bearingless switched reluctance generators [J]. IEEE Trans Appl Supercond, 2010,20 (3)： 1072-1076.

[6]CHIBA A, ASAMA J. Inuence of rotor skew in induction type bearingless motor [J]. IEEE Trans Magn, 2012,48(11)： 4646- 4649.

[7]FERREIRA J M S, ZUCCA M, SALAZAR A O, et al. Analysis of a bearingless machine with divided windings [J]. IEEE Trans Magn, 2005,41(10)： 3931-3911.

[8]李冰,邓智泉,严仰光.无轴承异步电机的最大径向力有限元分析[J].中小型电机，2003,30(3)： 20-24.

[9]朱熀秋,李元飞.无轴承同步磁阻电机设计及有限元分析[J].江苏大学学报(自然科学版),2011,32(3)： 331-335.

[10]陈世坤.电机设计[M].北京： 机械工业出版社，2000.

*基金项目：国家自然科学基金资助项目(61174055);国家自然科学基金资助项目(51307072)

作者简介：孙宇新(1968—)，女，博士研究生，副教授，研究方向为电机设计及控制。

中图分类号：TM 343

文献标志码：A

文章编号：1673-6540(2016)06- 0023- 05

收稿日期：2015-11-20

Performance Analysis on Torque and Suspension Force of Bearingless Induction Motor Bar*

SUNYuxin,WANGHao

(College of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China)

Abstract：Based on the working principle of BI motor with outer rotor, the mathematics model of the motor was deduced. Then, the distribution of magnetic field is simulated by FEM, and the relationship among radial suspension force, torque and rotor bar numbers was determined. Effects of magnetic saturation and bar dimensions on radial suspension force and torque were also studied. The results showed that torque ripple and suspension force ripple were influenced by rotor bar numbers. And relationshjp between average torque and average suspension force versus bar dimensions was affected by magnetic saturation.

Key words：bearingless motor; bar; finite element analysis; induction motor; model; outer rotor

王浩(1990—)，男，硕士研究生，研究方向为无轴承电机设计与控制系统。