角钢连接件剪切刚度计算方法及试验研究

邓文琴，张建东，刘　朵，胡　隽

（1.华中科技大学 土木工程与力学学院，湖北 武汉 430074；2.苏交科集团股份有限公司，江苏 南京 211112；3.东南大学 土木工程学院，江苏 南京 210096）

角钢连接件剪切刚度计算方法及试验研究

邓文琴1，张建东2，3，刘朵2，胡隽1

（1.华中科技大学 土木工程与力学学院，湖北 武汉 430074；2.苏交科集团股份有限公司，江苏 南京 211112；3.东南大学 土木工程学院，江苏 南京 210096）

鉴于角钢连接件剪切刚度的重要性，基于弹性地基梁理论推导了角钢连接件的等效剪切刚度计算公式，设计制作了3个角钢连接件试件进行推出试验，根据国、内外剪力连接件剪切刚度计算方法进行计算，将各方法计算结果与本文公式计算结果进行对比并就其适用性进行讨论分析。分析结果表明：国内、外连接件剪切刚度计算方法差异较大，日本规范计算结果与本文提出公式计算结果较为吻合，我国钢结构设计规范和0.8 mm割线法计算所得结果偏于安全，弹性阶段抗剪连接件的剪切刚度计算采用日本规范和本文公式计算比较合理。

角钢连接件；弹性地基梁；推出试验；剪切刚度

随着现代桥梁工程不断向轻质、高强、施工快捷等目标推进，钢-混组合结构得到迅速的发展［1］。波形钢腹板预应力混凝土组合箱梁结构由于其受力明确、自重轻、造型美观、施工方便等优点，越来越受到国内外工程界的重视［2-3］。波形钢腹板预应力混凝土组合箱梁最显著的特点是用波形钢腹板取代了混凝土腹板，其波形钢腹板与混凝土顶底板的连接是设计的关键环节，它直接关系到整个组合梁的承载能力［4-7］。其中角钢连接件（见图1）因其具有较好的承载力、抗剪刚度且施工方便，越来越受到国内工程界的重视。目前对组合结构的研究，特别是针对连接件的研究仅限于连接件的承载能力，而忽略了连接件刚度的影响［8］。随着对组合结构研究的深入，发现连接件刚度对组合结构的受力和变形都会产生一定的影响，在一些组合结构的规范中增加了对结构分析必须考虑连接件刚度的规定［9-11］，但仅限于栓钉连接件［12］，有关角钢连接件剪切刚度的研究和规定鲜有报道。

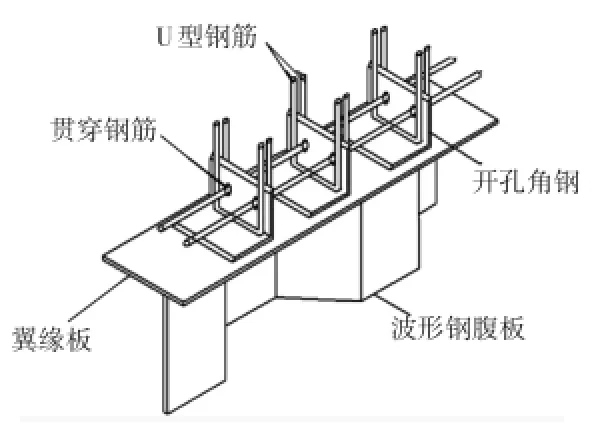
图1 角钢连接件

本文基于弹性地基梁理论推导了角钢连接件等效剪切刚度计算公式，并结合某实桥的抗剪连接件，进行角钢连接件推出试验，对日本规范、钢结构设计规范、0.8 mm割线法及本文提出公式计算所得剪切刚度进行对比，并对各公式适用性进行讨论分析。

1 等效初始刚度理论推导

1.1 基本假定

角钢连接件在混凝土中工作接近“弹性地基梁”，其与混凝土间的相互作用是通过其间的局部承压来平衡的［13］。设角钢连接件的布置形式如图2所示。

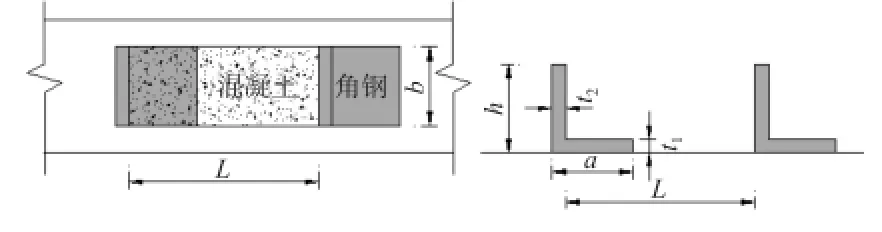
图2 角钢连接件布置图

推导过程中引入变形假设：

（1）混凝土和钢结构之间相对位移δ是由角钢和混凝土的变形引起的；

（2）角钢受力示意图如图3所示。

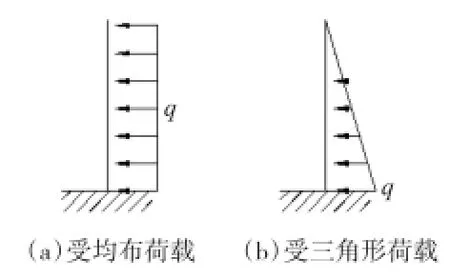
图3 角钢受力示意图

（3）角钢间混凝土的变形如图4所示，混凝土为纯剪切状态，在整个区域内均匀分布，剪切应变 γc=δ/h。

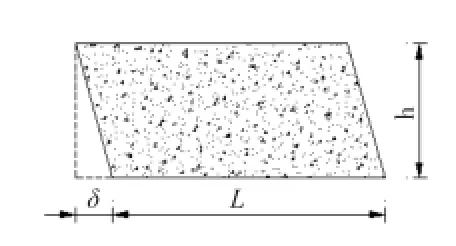
图4 混凝土剪切变形

1.2 等效初始刚度的推导

在简化分析中，将角钢与混凝土的抗剪连接件模拟为抗剪弹簧，其刚度为k。等效原则为当产生相对滑移δ时，角钢及角钢间混凝土变形产生的应变能与抗剪弹簧的应变能相等，即：

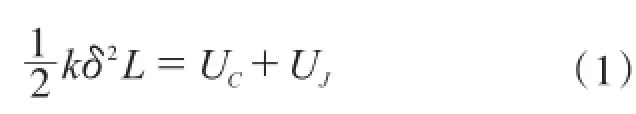
式中：UC和UJ分别为混凝土和角钢的应变能；δ为角钢自由端挠度；k为刚度系数。根据假设（3）可知，混凝土的应变能为：

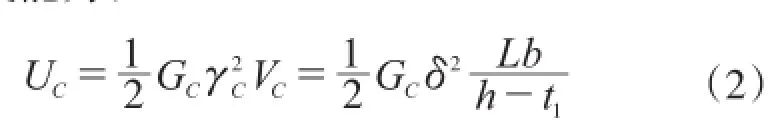
式中：VC为混凝土区域的体积，当L大于h时取L=h；GC为混凝土的剪切模量。

（1）假定角钢受力形式为均布荷载

角钢在均布荷载q作用下变形为：

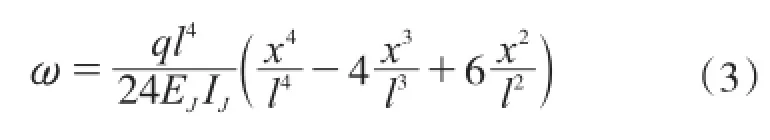
式中：EJIJ为角钢的抗弯刚度。

自由端挠度δ为：

故角钢的变形为：

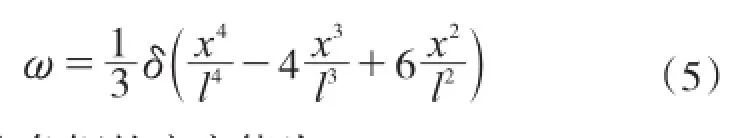
可以得出角钢的应变能为：

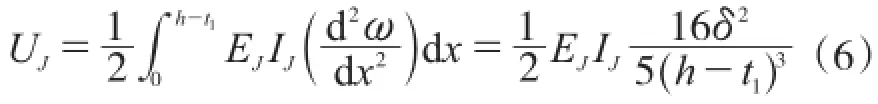
将式（2）和式（6）代入式（1）可得

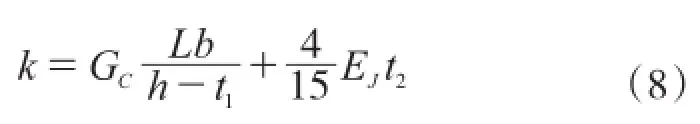
（2）假定角钢受力形式为三角荷载

角钢在三角荷载q作用下的变形为：

自由端挠度δ为：

故角钢的变形为：

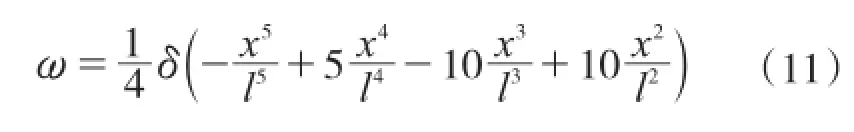
可以得出角钢的应变能为：

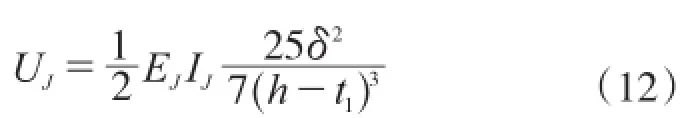
将式（2）和式（12）代入式（1）可得：

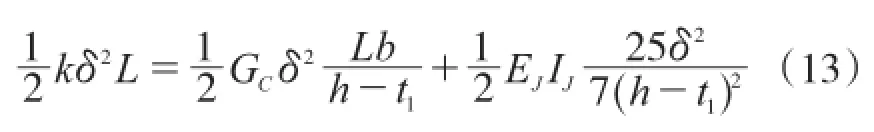
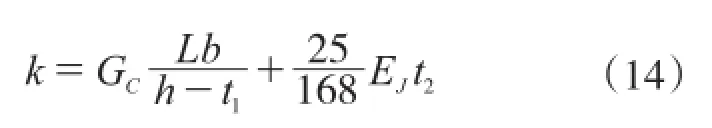
2 推出试验概况及分析

2.1 试件概况

试验设计基于某实桥初始设计方案中底板连接件的尺寸和设计要求，材料为Q345B钢，屈服强度为400 MPa，极限强度为520 MPa，弹性模量为1.95×105 MPa，采用1∶1足尺试件，设计了3个角钢连接件的推出试件（JG-1、JG-2、JG-3）。同时，浇筑了100 mm×100 mm×100 mm与实桥等强度的C50混凝土立方体试块，与推出试件同时养护，测试其28 d龄期抗压强度为40.26 MPa，剪力件尺寸和试件构造如图5所示。

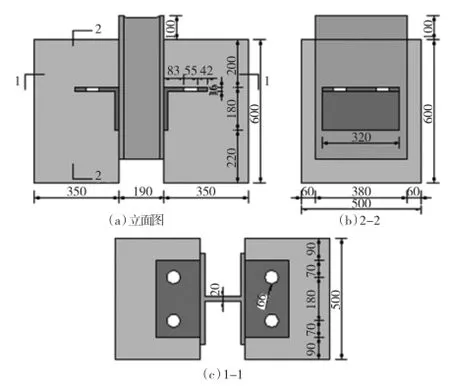
图5 连接件试件尺寸（单位：mm）

2.2 加载方法

加载分为预加载和正式加载两部分，加载过程遵循欧洲规范Eurocode4的标准，预加载阶段将荷载加到极限荷载的40%，持续一段时间，待位移计稳定后，卸载到极限荷载的5%，如此循环5次，每次持续2 min。待预加载完成，确保各仪表读数正常后，进行正式加载，正式加载分级进行，每一级以极限荷载的10%为增量，当加载至极限荷载的90%以后，加载采用位移控制直至试件破坏。记录每级加载、卸载过程所对应的位移计实际荷载，加载装置采用液压式四柱压力试验机，如图6所示。

2.3 试验结果及分析

荷载-位移曲线是反映抗剪连接件剪切刚度的一个重要指标，本次推出试验分别在加载工字型钢与混凝土侧面布设4个竖向位移测点，测试钢-混凝土相对滑移量，取平均值绘制各试件的荷载-位移曲线，如图7所示。

图6 试验加载

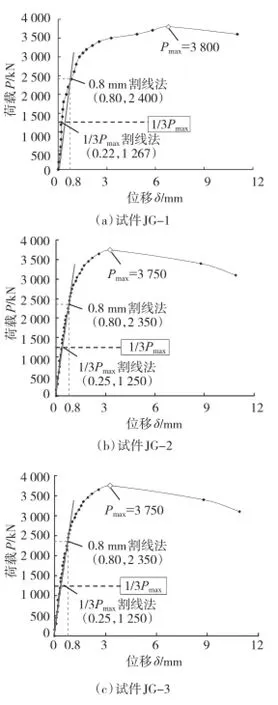
图7 推出试验荷载-位移曲线

试验结果表明，整个加载过程中，3个角钢试件都经历了3个阶段。第1阶段：弹性阶段，在该阶段荷载与位移基本呈线性关系，随着荷载的不断增大，位移变化很小，抗剪连接件表现出很大的抗剪刚度；第2阶段：弹塑性阶段，在该阶段位移随着荷载的不断增加呈非线性增加，此时荷载增加变缓，位移量大幅度增加，试件的抗剪刚度不断退化；第3阶段：荷载下降阶段，该阶段荷载开始缓慢下降，位移量持续大幅增长。从图7中还可以看出，3个试件破坏荷载均为3 550～3 800 kN，结果相差不大，且在加载到1/3Pmax荷载前，试件荷载-滑移曲线呈线性关系，说明试件还处于弹性阶段；当滑移达到0.8 mm时，试件荷载-滑移曲线已经呈非线性关系，试件产生了刚度退化现象。

3 剪切刚度计算方法

3.1 规范及文献计算方法

（1）日本规范

日本钢结构协会规定剪力连接件的抗剪刚度计算是依据每个连接件承担的剪力与滑移量的关系曲线，将通过最大抗剪承载力1/3大小处的割线刚度作为抗剪刚度［14］。该方法的计算结果是对应正常使用极限状态下的剪力连接件剪切刚度。采用该方法计算需要依赖于推出试验获得荷载滑移曲线。

（2）钢结构设计规范（GB50017—2003）

《钢结构设计规范》（GB50017—2003）11.4.3中提到抗剪连接件刚度系数k按如下公式计算：为角钢连接件的承载力设计值，即认为连接件在达到承载力设计值时，其滑移量为1 mm。

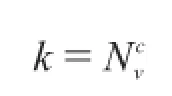
（3）0.8 mm割线法

Wang Y C在总结分析其所获得的试验数据及其他学者的试验数据后，结合剪力连接件的受力情况，提出采用设计承载力并取等效滑移量为0.8 mm的割线刚度作为剪力连接件的抗剪刚度［15］。

3.2 剪切刚度方法比较

表1为采用各种方法计算得到的角钢连接件剪切刚度值。

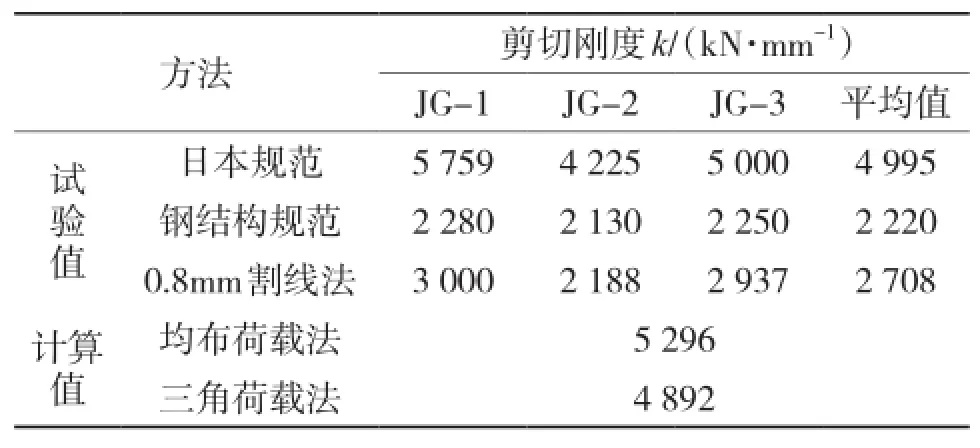
表1 试件剪切刚度值

由表1可知，按照日本规范计算得到的角钢剪切刚度值为4 995 kN/mm，该规范建议采用1/3极限承载力与滑移量的比值来计算连接件的剪切刚度，物理概念清晰。钢结构设计规范和0.8 mm割线法计算所得的剪切刚度值分别为2 220 kN/mm和2 708 kN/ mm，远小于日本规范计算值。本文中提出的2种剪切刚度等效刚度计算所得值分别为5 296 kN/mm和4 892 kN/mm，与日本规范计算值比较接近。钢结构规范和0.8 mm割线法计算剪切刚度值对应的连接件滑移量分别为1 mm和0.8 mm，根据钢筋混凝土结构规范中在正常使用状态下混凝土最大裂缝宽度为0.2 mm的要求，实际上当剪力连接件滑移量达到0.8 mm以前，荷载-滑移关系已经变为非线性关系，采用这2种方法计算的剪力连接件剪切刚度结果偏小。根据组合梁的设计和计算理论，组合梁的挠度计算需要考虑抗剪连接件的刚度，而组合梁的挠度问题属于正常使用极限状态范畴，因此，按弹性计算得到的剪切刚度较为合理。由上述分析可知，采用日本规范和本文公式计算角钢连接件抗剪刚度较为合理。

4 结语

（1）分别假定角钢连接件弹性状态下受力模式为均布荷载和三角荷载，推导了角钢连接件的等效初始刚度计算公式，计算结果同日本规范提出的公式符合较好。

（2）角钢连接件荷载-位移曲线均经历了线性变化、非线性变化及荷载下降3个阶段；各试件荷载-位移曲线趋势基本一致，但随机性较大，因此，通过荷载-位移曲线来确定角钢连接件剪切刚度离散性较大。

（3）国内、外关于剪力连接件研究方法差异较大，采用我国钢结构设计规范和0.8 mm割线法计算角钢连接件的抗剪刚度偏于安全；本文提出的计算式与日本规范公式计算结果与试验结果符合较好。

［1］石宵爽，王清远，欧阳雯欣，等.PBL剪力连接件粘结滑移性能的静载推出试验研究［J］.工程力学，2012，29（1）：168-175.

［2］杨明，孙筠，张树仁，等.波纹钢腹板体外预应力箱梁桥的发展与展望［J］.公路交通科技，2006，23（12）：72-75.

［3］万水，李淑琴，马磊.波形钢腹板预应力混凝土组合箱梁结构在中国桥梁工程中的应用［J］.建筑科学与工程学报，2009，26（2）：15-20.

［4］Eray Baran，Cem Topkaya. Behavior of steel-co-ncrete partially composite beams with channel t-ype shear connectors［J］. Joural of Constructional Steel Research，2014，97：69-78.

［5］Candido-Martins J P S，Costa-Neves L F，Vellasco P C G da S. Experimental evaluation of the structural response of Perfobond shear connectors［J］. Engineering Structures，2010，32：1976-1985.

［6］Eray Baran，Cem Topkaya.An experimental study on channel type shear connectors［J］. Joural of Constructional Steel Research，2012，74：108 -117.

［7］ 倪伟楠，刘朵，张建东，等.波形钢腹板嵌入式连接件力学性能试验研究［J］.世界桥梁，2014，42（2）：70-75.

［8］苏庆田，汪瑞，王巍.波折开孔板连接件基本力学性能试验［J］.中国公路学报，2012，25（2）：46-52.

［9］OGUEJIFOR E C，HOSAIN M U，Numerical analysis of pushout specimens with perfobond rib connectors［J］.Computers & Structures，1997，62（4）：617-624

［10］OGUEJIFOR E C， HOSAIN M U. A parametric study of perfobond rib shear connectors ［J］. Canadian Journal of Civil Engineering，1994，21（4）：614-625.

［11］ EN 1994-Eurocode 4. Design of composite steel and concrete structures［S］.

［12］姬同庚.栓钉连接件剪切刚度试验研究［J］.世界桥梁，2013，41（6）：62-66.

［13］张石波.考虑滑移效应的钢-混凝土组合梁桥力学行为研究［D］.广州： 华南理工大学，2012.

［14］刘玉擎.组合结构桥梁［M］.北京：人民交通出版社，2005.

［15］Wang Y C. Deflection of steel-concrete composite beam with partial shear interaction ［J］. Journal of Structural Engineering，1998，124（10）：1159-1165.

Study of Calculation and Experiment for Shear Stiffness of Angle Steel Connector

Deng Wenqin1， Zhang Jiandong2，3， Liu Duo2， Hu Jun1
（1.Department of Civil Engineering & Mechanics， Huazhong University of Sci &Tech， Wuhan 430074， China；2. JSTI Group， Nanjing 211112， China； 3. College of Civil Engineering， Southeast University， Nanjing 210096， China）

Derived the equivalent shear stiffness calculation formulas of angle connector based on theory for beam on elastic foundation in view of their importance. Three angle connectors were designed and made for push-out test. In accordance with the domestic and foreign methods for shear stiffness calculation， shear stiffness values were calculated and compared with the results from this article， their applicability were also discussed and analyzed. The results of the analysis show that there are great difference between differents shear stiffness calculation methods in China and other countries. The methods of the Japanese specification and the results calculated in this paper were in good agreement. The calculation methods of Chinese code for design of steel structures and the 0.8mm secant method which are relatively conservative used to calculate the shear stiffness of angle connector. The method of Japanese specification and the formulas of this paper used to calculate the shear stiffness in the elastic stage were reasonable.

angle connector； beam on elastic foundation； push-out test； shear stiffness

U448.21+6

A

1672-9889（2016）01-0035-04

国家自然科学基金（项目编号：51478107）；江苏省交通科研项目（项目编号：2014Y01）

邓文琴（1991-），女，江西抚州人，博士研究生，研究方向为钢混组合桥梁。

2015-05-21）