液压弯辊控制参数对热连轧机振动能量影响研究

闫晓强， 么爱东， 刘克飞

(北京科技大学 机械工程学院，北京　100083)

液压弯辊控制参数对热连轧机振动能量影响研究

闫晓强， 么爱东， 刘克飞

(北京科技大学 机械工程学院，北京100083)

近年来，热连轧机振动问题显得更加突出和复杂化，众多企业迫切需要解决这一难题。首先对某热连轧机振动现象进行在线监测；然后依据轧机实际参数建立液压弯辊系统和轧机垂直系统的耦合动力学模型，利用MATLAB进行了仿真研究，通过改变液压弯辊系统中控制器参数，获得液压弯辊的控制性能对辊系振动能量的影响，实践表明这是有效抑制振动的措施之一。

热连轧机；液压弯辊；辊系；仿真；抑振

半个多世纪以来连轧机的振动问题在轧制领域备受关注。随着轧机装备水平不断提高，热连轧机呈现更复杂的多种现象并存的振动。某热连轧机组在轧制薄规格带钢时，轧机出现了严重的振动现象，其中以F3轧机振动最为剧烈，严重影响带钢表面质量，威胁轧机的安全生产。过去几十年对液压弯辊系统的研究主要集中在板形控制方面，忽略了液压弯辊系统控制参数对轧机振动能量的影响。为进一步研究轧机振动能量的影响因素，本文建立轧机液压弯辊系统和垂直系统的耦合动力学模型，试图从理论上解释液压弯辊系统控制参数对轧机振动能量影响的规律。

1轧机振动监测

当热连轧机轧制薄规格带钢时，对F3轧机上工作辊和上支承辊的轴承座的垂直、水平和轴向三个方向的振动加速度信号进行了大量的跟踪测试。发现轧机出现强烈振动时，水平方向振动能量最大、垂直方向次之、轴向最小，其主要振动基频约为45 Hz如图1所示。

图1　F3轧机上辊系振动加速度波形及频谱图Fig.1 Upper roller system acceleration waveform diagram and spectrum diagram of F3 rolling mill

经过分析发现：现场在线采集的CVC缸外壳、液压弯辊系统伺服阀电流信号和弯辊力信号中均出现了与辊系一致的振动优势频率如图2～图4所示。说明辊系与液压弯辊系统产生了耦合振动关系，下面试图从仿真来解释这种振动现象及抑振措施效果。

图2　CVC缸外壳加速度及频谱图Fig.2 CVC cylinder shell acceleration waveform and spectrum diagram

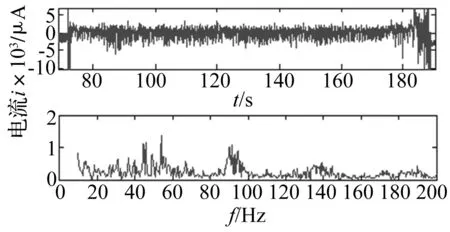
图3　液压弯辊伺服阀电流波形及频谱图Fig.3 Servo valve current waveform and spectrum diagram of Hydraulic bending roll

图4　弯辊力波形及频谱图Fig.4 Bending roll force waveform and spectrum diagram

2液压弯辊模型的建立

该液压弯辊系统由给定信号PI控制器送到，经过放大器和电液伺服阀来控制液压缸动作。调节伺服阀阀芯的开口方向和大小来控制液压油的流量使液压缸动作。通过工作辊轴承座完成工作辊弯辊力大小的调节如图5所示。液压弯辊力反馈控制采用液压缸无杆腔液压压力传感器信号反馈到PI控制器给定，以完成对弯辊力的调节。

图5　液压弯辊系统控制原理图Fig.5 Control principle of hydraulic bending roll system

2.1伺服阀模型的建立

热连轧机液压弯辊控制系统采用PI控制器，其传递函数为：

(1)

式中Ka比例系数；Kb积分系数。

伺服放大器将输入的信号放大，可近似视为比例放大环节，其传递函数为：

(2)

式中:Ue伺服放大器输出电压；Uo伺服放大器输入电压。

伺服放大器输出电压加在电液伺服阀内的力矩马达线圈上，衔铁在线圈的磁场中作偏摆运动时线圈中也会产生反电动势，则传递函数可表示为：

(3)

式中:ra、rb为感应线圈电阻；Δi为力矩马达中电流；Lb为感应线圈电感。

反馈弹簧杆推动先导阀运动传递函数为：

(4)

式中Kt为力矩马达的力常数；Kf为反馈弹簧杆的等效刚度；Kog为开环增益；ωmf为力矩马达的固有频率；ξmf为力矩马达的阻尼比；xv为先导阀阀芯位移。

对主阀芯进行受力分析，由于主阀芯主要受液动力、阀芯惯性力和阀芯两侧压力，因此有：

(5)

式中Ap为主阀芯横截面积；Mp为主阀芯质量；xp为主阀芯位移；w为主阀芯面积梯度；ps为系统供油压力；p为伺服阀出口压力；kap为先导阀零位处的压力流量系数；kp为先导阀零位处的流量增益。

当先导阀在零位时，先导阀位移为零，压力-流量系数可忽略不计，因此，式(5)可转化为：

kpxv=ApSxp

(6)

主阀芯位置反馈方程为：

Δif=Bfxp

(7)

式中Bf为位置反馈增益系数。

压力传感器的数学模型为：

Vf=KFPl

(8)

式中KF为压力传感器增益系数；p1为弯辊缸无杆腔油压。

2.2液压弯辊缸模型的建立

热连轧机液压弯辊系统中液压缸属于非对称缸，伺服阀控制液压缸上下移动从而对工作辊施加弯辊力。当弯辊缸对工作辊施加弯辊力时，油液注入到无杆腔，此时主阀芯位移为正，由流体力学知识可知主阀芯流量方程：

(9)

式中Q2为流入无杆腔的流量；Q1为流出有杆腔的流量；cd为流量系数；wp为伺服阀阀芯面积梯度；p2为弯辊缸无杆腔油压；p1为弯辊缸有杆腔油压。

考虑到液压缸泄漏和油液压缩，流入无杆腔的流量和输出有杆腔的流量有：

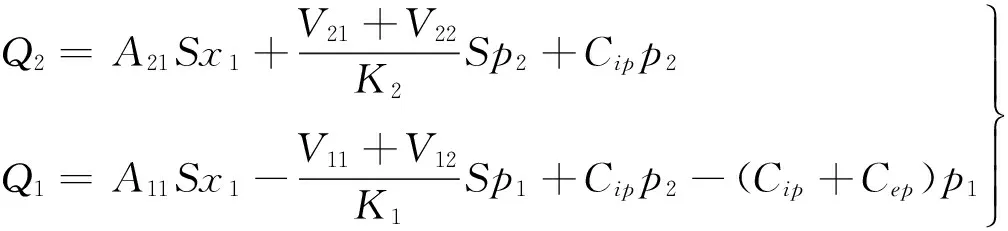
式中x1为液压缸位移；Cip为液压缸内泄系数；Cep为液压缸外泄系数；K1、K2为液压油体积弹性模量。V11为弯辊缸无杆腔油液体积；V12为弯辊缸无杆腔出口管路油液体积；V21为弯辊缸有杆腔油液体积；V22为弯辊缸有杆腔出口管路油液体积。

液压弯辊缸的动力学方程为：

(11)

式中m2为轧辊及其轴承座的等效质量；kw为液压弯辊系统的等效刚度；cw为液压弯辊系统的等效阻尼；F为其它外作用力。

3轧机弯辊动力学模型建立

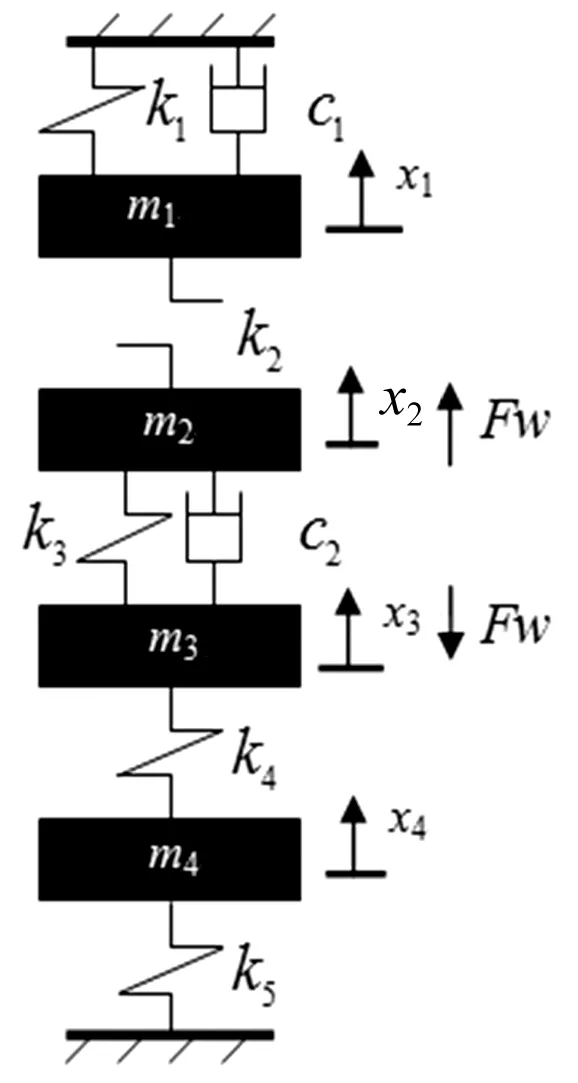
图6　轧机弯辊动力学模型Fig.6 Model of rolling mill bending roll system

以F3轧机为研究对象，将轧机垂直系统简化为四质量和五弹簧的四自由度系统如图6所示。

由此可以得出垂直系统的振动方程如下：

(12)

式中m1为液压压下装置、垫块、上支承辊、上支承辊轴承及轴承座横梁及立构牌坊上的等效质量；m2为上工作辊、上工作辊轴承及轴承座的等效质量；m3为下工作辊、下工作辊轴承及轴承座的等效质量；m4为下支承辊、下支承辊轴承及轴承座牌坊下横梁的等效质量；k1为液压压下系统、牌坊立柱及上横梁的等效刚度；k2为上支承辊轴承及轴承座、上支承辊弯曲、上支承辊和上工作辊之间的弹性压扁等效刚度；k3为上、下工作辊的弹性压扁刚度，轧件弹塑性变形刚度；k4为下支承辊轴承及轴承座、下支承辊弯曲、下支承辊和下工作辊之间的弹性压扁等效刚度；k5为下支承辊轴承座至下横梁的等效刚度；c1为液压压下系统的等效阻尼；c2为上、下工作辊与带钢之间的等效阻尼；xi为各集中质量的振动位移(i=1,2,3,4)；FW为弯辊缸作用于工作辊轴承座的弯辊力。

4耦合振动模型的建立

依据所建立的轧机四自由度垂直模型和液压弯辊系统模型，建立轧机垂直系统和液压弯辊系统的耦合动力学模型如图7所示。

5耦合振动系统仿真研究

5.1给定信号时耦合系统响应

在进行现场轧机测试时，发现液压弯辊伺服阀电流信号是振荡的，并且和轧机垂直系统振动相一致的频率成分(图3)。液压弯辊伺服阀电流信号如图8所示，可以看作是由多个不同频率的正弦信号的叠加。对该进行非线性拟合，拟合后的波形及频谱图如图9所示，其数学表达式为：

f(t)=a0+a1sin(2πf1t)+

a2sin(2πf2t)+a3sin(2πf3t)+

a4sin(2πf4t)+a5sin(2πf5t)+a6sin(2πf6t)

(13)

式中，f1=6 Hz、f2=19 Hz、f3=45 Hz、f4=57 Hz、f5=84 Hz、f6=120 Hz。运用MATLAB编程可求得拟合后的系数：a0=4.23×10-7、a1=2.51×10-3、a2=1.63×10-3、a3=-1.34×10-3、a4=1.12×10-3、a5=0.79×10-3、a6=0.52×10-3。

将拟合后的信号作为液压弯辊系统仿真模型的给定信号来观察辊系输出信号。仿真后得到上工作辊位移响应和加速度响应波形及频谱图如图10所示。

对比图9和图10可以发现给定信号的频率在辊系的振动响应信号中仍然存在。图10中可以看出在位移信号中6 Hz的低频最明显，其次是19 Hz和45 Hz，57 Hz和84 Hz相对较弱，而120 Hz的高频几乎看不见了。在加速度信号中45 Hz、57 Hz以及84 Hz最为明显， 这与监测的轧机振动频率相近。由此可以推断液压弯辊系统给定信号的振荡将影响轧机辊系振动能量，从而判定液压弯辊系统控制性能对轧机振动存在一定的影响。

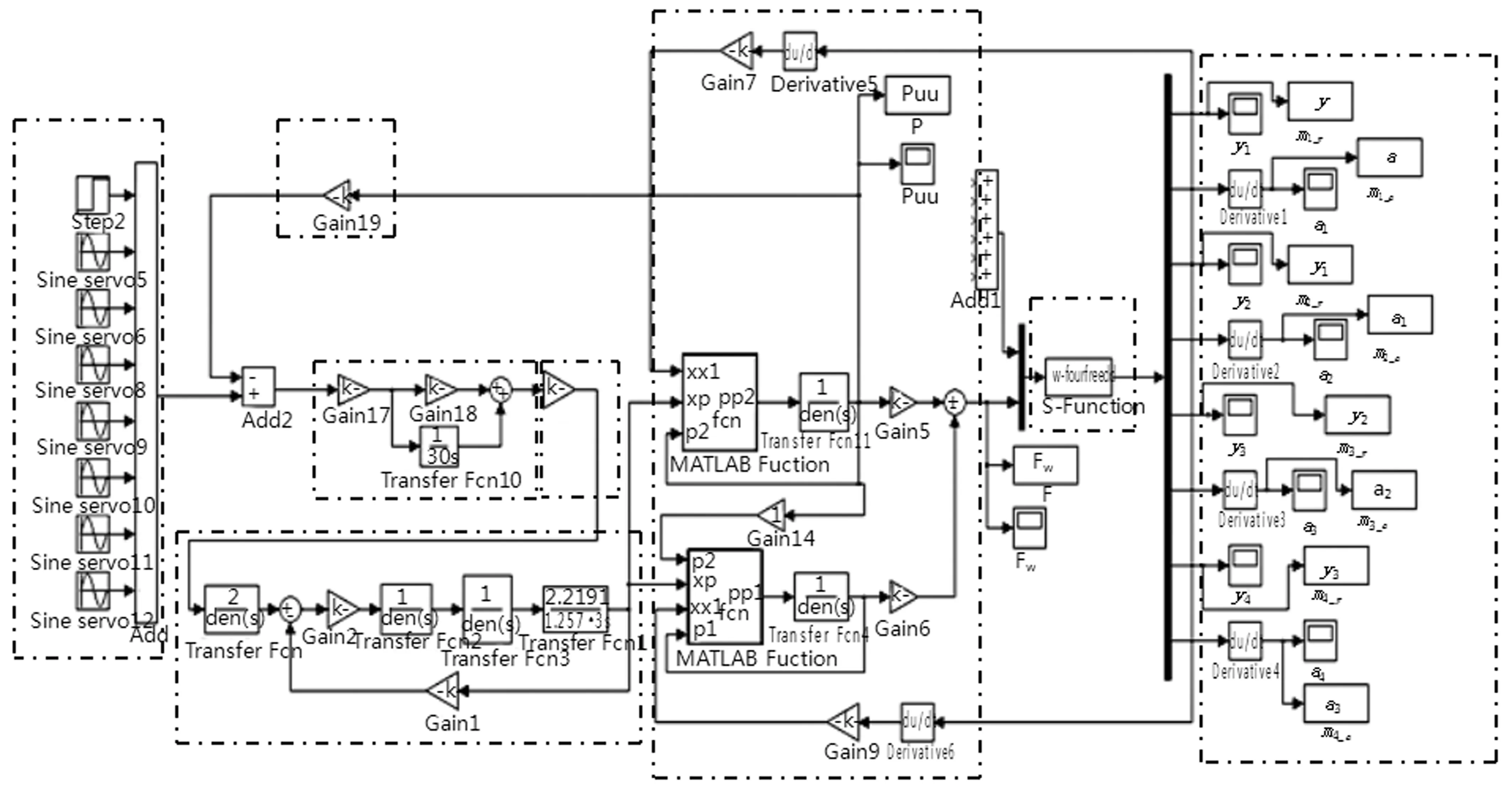
1.给定信号；2.PI控制器；3.伺服放大器；4.伺服阀；5.液压弯辊缸模型；6.轧机四自由度垂直系统；7.压力传感器；8.系统相应输出图7　轧机液压弯辊系统和垂直系统耦合动力学仿真模型Fig.7 Coupling vibration model of rolling mill vertical system and hydraulic bending roll system

图8　液压弯辊伺服阀电流信号波形Fig.8 Servo valve current waveform diagram of Hydraulic bending roll

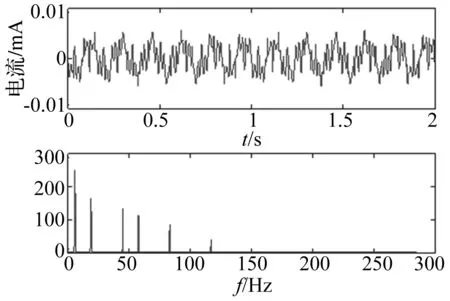
图9　拟合后的液压弯辊系统伺服阀电流信号波形及频谱图Fig.9 After fitting the servo valve current waveform diagram and spectrum diagram of Hydraulic bending roll

图10　上工作辊位移和加速度波形及频谱图Fig.10 Upper roller series acceleration waveform diagram and spectrum diagram

5.2耦合系统的相频特性分析

在不同频率20～110 Hz给定信号作用下，获得耦合系统的位移响应和加速度响应与给定信号的相位差如图11和图12所示。

图11　上工作辊位移相频特性Fig.11 Displacement phase frequency characteristic of the upper roller series

图12　上工作辊加速度相频特性Fig.12 Acceleration displacement phase frequency characteristic of the upper roller series

从图11,12中可以看出：在不同频率的给定信号作用下，耦合系统的位移响应均滞后于给定信号且滞后相位较大。系统的加速度响应在较低频率时超前于给定信号，较低高频率时滞后于给定信号。这是因为系统的加速度响应是位移响应的二阶求导，所以系统的加速度响应和位移响应相位差为180°。由此可知当系统的响应滞后于给定信号较大时就会影响整个系统的稳定性，进而影响整个轧机在轧制过程中的稳定，从而加剧轧机的振动。因此给定信号优劣和液压弯辊系统特性都会影响轧机的振动。

6基于耦合模型的振动能量影响因素研究

液压弯辊系统中可以改变的参数主要是PI控制器中的比例环节和积分环节。该F3轧机液压弯辊系统的比例环节的控制参数为1～70，积分环节控制参数范围为0.001～1000。

6.1比例常数对耦合系统振动影响

保持积分常数I原始值不变，改变比例环节P由1到100之间变化，上工作辊及上支承辊加速度响应及位移响应如图13和图14所示。

图13　上工作辊和上支承辊加速度响应随P值变化曲线Fig.13 Curve of acceleration response change with P values of the upper work roller and upper support roller

图14　上工作辊和上支承辊位移响应随P值变化曲线Fig.14 Curve of displacement response change with P values of the upper work roller and upper support roller

由图13,14可以看出：随着P值的增大上工作辊的加速度和位移响应以及上支承辊的加速度和位移响应均随之增大，也就是随着P值的增大，轧机辊系振动加剧。所以在实际中应尽量减小比例环节P的值，以减小液压弯辊系统对轧机辊系振动的影响。但是P值过小(如图15)，在阶跃给定信号下，上工作辊位移响应的响应速度过慢。通过仿真计算可以得出当P值为5～15时不仅满足控制系统的稳定性和快速性要求，而且能有效的减小液压弯辊系统对轧机振动的影响。

图15　不同P值下上工作辊位移阶跃响应Fig.15 Displacement step response of the upper work roller under different P values

6.2积分常数对耦合系统振动影响

保持比例环节P值不变，使积分环节I值从0.001到1 000之间变化，上工作辊及上支承辊加速度响应及位移响应如图16和图17所示。

图16　上工作辊和上支承辊加速度响应随Ⅰ值变化曲线Fig.16 Curve of acceleration response change with Ⅰ values of the upper work roller and upper support roller

由图16,17可以看出：随着Ⅰ的增大,上工作辊和上支承辊加速度响应和位移响应随之减小，但是当Ⅰ值大于1以后上工作辊和上支承辊加速度响应和位移响应基本不变。

图17　上工作辊和上支承辊位移响应随P值变化曲线Fig.17 Curve of displacement response change with Ⅰ values of the upper work roller and upper support roller

7抑振措施实施

为验证上述仿真结果，在现场进行了参数调节与振动测试，保持其它工艺等参数不变，只改变液压弯辊系统中PI控制器中的比例参数P值，监测的辊系振动加速度如图18～图20所示。

图18　F3轧机上辊系振动加速度波形及频谱图(P=60)Fig.18 Upper roller series acceleration waveform diagram and spectrum diagram of F3 rolling mill(P=60)

图19　F3上辊系振动加速度波形及频谱图(P=30)Fig.19 Upper roller series acceleration waveform diagram and spectrum diagram of F3 rolling mill(P=30)

图20　F3上辊系振动加速度波形及频谱图(P=10)Fig.20 Upper roller series acceleration waveform diagram and spectrum diagram of F3 rolling mill(P=10)

为了清晰起见，依据图18～20得到不同P值对应的上工作辊垂直方向加速度、上工作辊水平方向加速度和上支承辊水平方向加速度如图21所示。

由图21可以看出：对P值进行调试时，随着P值的减小，辊系加速度振动幅值也随之减小。上工作辊垂直方向加速度幅值减小了15%，上工作辊水平方向加速度幅值减小了29.9%，上支承辊水平方向加速度幅值减小了17.1%。由此可以看出通过改变P值可以有效降低液压弯辊系统对轧机振动能量的影响。

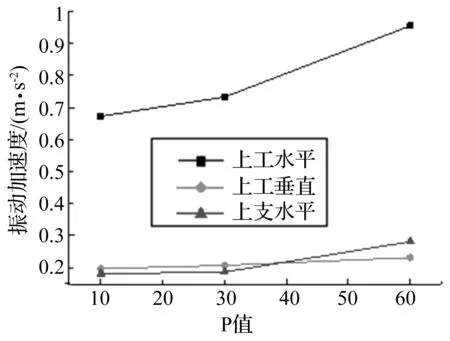
图21　不同P值下上振动加速度幅值Fig.21 Acceleration amplitude the upper roller series under different P values

8结论

依据现场测试及信号分析，发现液压弯辊系统的振动与轧机辊系的振动存在耦合振动关系。为了解释这一现象，本文建立了液压弯辊系统和轧机辊系的耦合动力学模型，通过仿真研究获得：液压弯辊系统的调节参数值会影响轧机振动能量的大小。实践表明：调节液压弯辊控制器参数值是降低轧机振动能量的有效措施之一。

[1] 闫晓强, 史灿,曹曦. CSP轧机扭振与垂振耦合研究[J].振动、测试与诊断, 2008,28(4):377-381.

YAN Xiao-qiang,SHI Can,CAO Xi.Research on CSP rolling mill coupling of torsional vibration and vertical vibration[J]. Vibration Measurement & Diagnosis, 2008,28(4):377-381.

[2] Yan Xiao-qiang,Sun Zhi-hui,Chen Wei.Vibration control in thin slab hot trip mills[J].Iron Making and Steelmaking,2011,38(4):309-313.

[3] 刘浩然, 侯东晓, 时培明.轧机辊系滞后非线性垂直振动系统的振动特性[J].机械工程学报, 2011,47(13):65-70.

LIU Hao-ran,HOU Dong-xiao,SHI Pei-ming. Vibration characteristics of hysteretic nonlinear vertical vibration systerm of rolling mill roller[J]. Chinese Journal of Mechanical Engineering,2011,47(13): 65-70.

[4] 闫晓强.热连轧机机电液耦合振动控制[J].机械工程学报, 2011,47(17)：61-65.

YAN Xiao-qiang. Machinery-electric-hydraulic coupling vibration contrlo of hot continuous rolling mills[J]. Chinese Journal of Mechanical Engineering,2011,47(17):61-65.

[5] 宋泽红,凌启辉,张秀华.轧机液压压下谐响应特性研究[J].冶金设备,2012(5):20-23.

SONG Ze-hong, LING Qi-hui,ZHANG Xiu-hua. Study on the characteristic of harmonic response about mill hydraulic screwdown system[J].Metallurgical Equipment,2012(5):20-23.

[6] 凌启辉,闫晓强,张清东,等.双动力源作用下热连轧机工作辊非线性水平振动特性研究[J].振动与冲击,2014,33(12):134-137.

LING Qi-hui,YAN Xiao-qiang,ZHANG Qing-dong,et al.Double power source under the action of hot tandem rolling mill nonlinear horizontal vibration characteristics [J].Journal of Vibration and Shock,2014,33(12): 134-137.

[7] 闫晓强,杨喜恩,吴先峰.轧机水平振动侧向液压振动抑制器抑振效果仿真研究[J].振动与冲击,2013,32(24):11-14.

YAN Xiao-qiang,YANG Xi-en,WU Xian-feng.Restraining vibration effect simulation of hydraulic Vibration suppression device for rolling mill horizontal direction [J].Journal of Vibration and Shock,2013,32(24):11-14.

Effect of hydraulic bending roll on vibration energy of a hot continuous rolling mill

YAN Xiao-qiang, YAO Ai-dong, LIU Ke-fei

(School of Mechanical Engineering, Beijing University of Science and Technology, Beijing 100083, China)

In recent years，hot continuous rolling mill vibration problems are more prominent, many enterprises urgently need to solve this problem. Here, the vibration problem of a hot continuous rolling mill was monitored online. Then, a coupled dynamic model of a rolling mill vertical system and a hydraulic bending roll system was built. According to the actual mill parameters. MATLAB was used to do a simulation study. The effects of the control performance of the hydraulic bending rolls system on the rollers system vibration energy were analyzed by changing the controller parameters of the hydraulic bending roll system. The results provided one of effective measures for suppressing vibrations of hot continuous rolling mills.

hot continuous rolling mill; hydraulic bending roll system; rolls system; simulation; suppressing vibration

10.13465/j.cnki.jvs.2016.11.007

国家十二五科技支撑计划(2015BAF30B01)

2015-02-02修改稿收到日期：2015-05-09

闫晓强 男，博士，教授，博士生导师，1961年11月生

TH212；TH213.3

A