应用位置敏感探测器检测平面度的方法研究*
韩金玉,王守志
(天津中德应用技术大学 a.电气与能源学院;b.航空航天与汽车学院,天津 300350)
应用位置敏感探测器检测平面度的方法研究*
韩金玉a,王守志b
(天津中德应用技术大学a.电气与能源学院;b.航空航天与汽车学院,天津300350)
摘要:为实现平面度误差值的在线检测,文章在分析平面度最小二乘法评定方法和位置敏感探测器测距原理的基础上,提出了一种基于应用直射式光学三角法的平面度在线检测方法,并设计了一种试验装置。该方法首先应用3组位置敏感探测器检测组件逐次检测被测表面的Z向偏离值,确定各被测点的坐标值,然后应用最小二乘法计算平面度,评定基准面后,计算平面度误差值。仿真试验结果表明,文中方法对于一般平面的测量精度较高,优于千分尺指示器法,其测量结果可靠有效。
关键词:平面度;检测;位置敏感探测器
0引言
平面度是产品的一种重要形位公差,其误差值大小对产品的工作质量和工作性能有着直接影响。间隙法、液面法、指示器法等传统的平面度检测方法检测评定步骤复杂,检测精度不高,较难实现在线连续测量[1]。为此,国内外学者应用CCD探测器提出了多种平面度测量方法,如陈宝刚等人基于光学及图像处理提出的内调焦平面度测量方法[2],陈小宁等人基于双目视觉和投影圆提出的非接触式测量方法[3],VMaurizio应用斜射式光学三角法提出了平面度迭代测量方法[4],LZhao等人提出的基于机器视觉的平面度测量方法和柔性校准方法等[5]。但这些平面度测量方法均采用了CCD探测器技术,其检测数据量大、响应速度慢,且斜射式光学三角法对表面粗糙度较为敏感,无法满足先进制造技术的发展需要。因此,本文应用具有成本低、响应快、分辨率高、线性精度高等多种优点[6]的位置敏感探测器(PositionSensitiveDetector,PSD),提出了一种对粗糙度敏感度低的直射式平面度测量方法。
1检测方法与系统设计
1.1平面度误差检测评定方法
平面度误差值是被测平面对理想平面的允许变动量,即用平面度最小包容区域的宽度f表示的数值[1],如图1所示。

图1 平面度误差
现有的平面度评定方法有多种,如最小二乘法、三远点平面法和对角线平面法等。本文选用计算快捷简单、应用广泛的最小二乘法评定平面度误差。最小二乘检测评定法的关键工作是测量实际平面上各测量点的位置,然后确定最小二乘中心平面SLS及各测量点相对于平面SLS的偏离值,然后以中心平面SLS作为评定基面,应用式(1)计算平面度误差值fLS。
fLS=dmax-dmin
(1)
式中,dmax、dmin为各测得点相对中心平面SLS的最大和最小偏离值。
1.2PSD检测原理
1.2.1PSD工作原理
位置敏感探测器(PositionSensitiveDetector,PSD)是一种基于半导体“横向光电效应”的光电位置敏感器件[7-8],可以连续检测光斑位置,且检测位置是光斑的能量重心位置,与光斑面积大小和能量分布无关。PSD有一维和二维两种类型,其工作原理均与光电二极管相似,为PIN结构[7],如图2所示。

图2 一维PSD结构
在光照射时,入射光照射位置P处将产生一个与光强成比例的电荷。假设光敏面的电阻层均匀分布,那么两个输出电极的光电流的关系为:
(2)
由(1)式可得:
(3)
式中,d为入射光照射位置P到PSD中心的偏移距离;I1为输出电极1的电流;I2为输出电极2的电流。
可见,理论上入射光相对于PSD中心的偏移距离与光敏面长度和输出电流值有关。检测时,可以通过检测两个输出电极的电流值,间接获得入射光相对于光敏面的位置。
但是,在实际检测过程中,PSD的检测精度受背景光、暗电流、入射光波长及光斑大小等多种因素的影响,呈非线性特点。本文选用抗干扰能力强、线性度好的S3979型一维PSD。S3979型PSD的峰值响应波长为920nm,波长在400nm~860nm时,其温度特性较好,而背景光主要是可见光,为避免背景光的干扰,在PSD前放置滤光片,滤除背景光,同时激光波长取800nm,光斑大小取φ0.2mm。此时,该PSD的温漂较小,为提高精测精度,采用阻容耦合电路进一步抑制温漂问题。
1.2.2PSD测距方法
激光三角测量是一种非接触测量位移的重要方法,广泛应用于三维轮廓、厚度、宽度及振动测量[9]。本文采用对表面粗糙度不敏感的直射式光学三角法测量实际平面的Z向偏移量,如图3所示。成像透镜用于收集入射光在被测物体表面的漫反射光线,并在PSD光敏面上成像。为使不同实际表面点在PSD光敏面上精确成像,应满足Scheimpflug条件,即PSD的光敏面、成像透镜的主平面与激光组件轴心线延长线应相交于一点[10-11]。

图3 光学三角形法原理图

由三角形相似原理可得:
则:
即:
(4)
若被测表面向下偏移时,PSD检测获得的偏移量d为负数,即k=-d。同理,可证明式(4)同样适用于向下偏移量的计算。
由式(4)可知,通过PSD光敏面的光斑偏移量d可以计算出被测表面的偏离值,且二者呈非线性关系。
1.3检测系统设计
1.3.1PSD检测装置设计
S3979型PSD的光敏面尺寸为3mm×1mm,位置分辨率0.1μm。激光源、聚光透镜、成像透镜、PSD等按图3所示的布局制作成相对位置固定的检测组件。
检测组件安装在固定支座上,如图4所示。为提高检测速度,并降低Y向误差,采用安装于同一高度的3个检测组件同时测量被测工件表面的Z向偏移量,其间距为10mm。检测时,移动支座、被测工件置于同一测量平台上,并垂直校准支架高度使至少一个检测组件成像于PSD光敏面中心点后,依此为基准,检测第一组检测点的高度偏移量,然后平移移动支座5mm,检测第二组检测点的高度偏移量,依此类推,直到检测完待测工件,如图5所示。
注意,因各被测点的垂直高度不同,检测前的校准一般无法保证3个检测组件都成像于PSD光敏面中心点。若强制使3个检测组件都成像于PSD光敏面中心点,会给检测结果带来较大的误差。

图4 检测装置

图5 检测布点方式
1.3.2检测方法设计
PSD光电信号经滤波调理电路调理后,由PCI-6040E数据采集卡采集数据,并上传计算机。检测数据由自行开发的VisualC++程序处理,确定最小二乘中心平面SLS后,计算出平面度误差值,其具体步骤如下:
(1)垂直校准后,检测第一组数据,应用式(3)和(4)分别计算各点的高度值,则可获得第一组3点的坐标值,记为P11=(0,0,z11)、P21=(0,10,z21)、P31=(0,20,z31);
(2)平移移动支座5mm,检测并计算第二组各检测点的高度值,各点坐标值记为P12=(5,0,z11)、P22=(5,10,z21)、P32=(5,20,z31),依此类推,将待测工件检测完。
(3)应用检测获得的各点坐标值计算确定最小二乘中心平面z=f(x,y);
(4)计算各检测点到相对中心平面SLS的最大偏离值dmax和最小偏离值dmin;
(5)应用式(1)计算平面度误差值。
2试验与分析
为了验证本文方法的有效性和测量精度,选择尺寸为22mm×200mm×30mm试验工件10块,分成2组,每组5块。设定2个试验,一组试验工件的22mm×200mm表面做研磨处理,另一组不做研磨处理,分别使用本文方法、千分表指示器法及L-740平面度检测仪(评测精度为0.0025mm/M)等3种方法测量3次被测表面的平面度误差值,用3次测量结果的平均值表示该种测量方法的测量结果,并以L-740平面度检测仪的测量结果fL为依据,按照式(5)评价本文方法及千分表指示器法测量结果的最大相对准确度。
(5)
对于一般精度的平面,测量结果如图6所示。与L-740平面度检测仪的测量结果相比,本文方法与其相近,最大差异为2.5μm,最大相对准确度为2.6%;千分尺指示器法差异较大,最大差异量为4.5μm,最大相对准确度为5.1%。由上分析可知,本文方法对于一般精度的平面,其测量结果接近与L-740平面度检测仪,优于千分尺指示器法,其测试结果有效可靠。
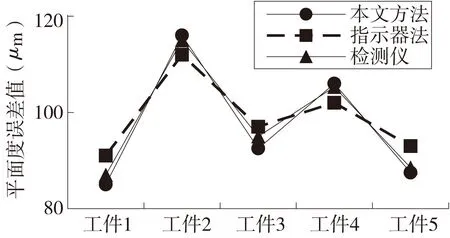
图6 未研磨工件的测量结果对比图
对于研磨后精度较高的平面,本文方法的测量结果与千分尺指示器法相近,最大差异量为2μm。与L-740平面度检测仪的测量结果相比,本文方法的最大差异量为3.2μm,最大相对误差为26.3%;千分尺指示器法最大差异量也为3μm,最大相对误差为18.7%,如图7所示。

图7 研磨工件的测量结果对比图
可见,对于精度较高的平面,本文方法的测量结果与千分尺指示器法接近,与L-740平面度检测仪对比,其相对误差较大。这是由于本文设计的检测装置没有补偿PSD自身的位置检测误差、校准误差及干扰信号引入的误差。若采取措施补偿PSD的非线性误差等可进一步提高测量精度,将适用于精度较高的平面检测。
3结论
本文提出的平面度检测方法可实现平面度的在线检测,且对一般平面其测量结果可靠有效。若配合水平定位在线控制装置,可以实现平面度的在线连续测量。
(1)入射光相对于PSD中心的偏移距离与光敏面长度和输出电流值有关,其偏离值可通过检测两电极的电流值确定。
(2)直射式光学三角法可以测量被测表面的Z向偏移量,且Z向偏移值与PSD光敏面的光斑偏离值成非线性关系。
(3)本文方法测量一般平面的精度较高,优于千分尺指示器法,其测量结果可靠有效。对于精度较高的平面,本文方法的相对测量误差较大,需采取误差补偿措施,提高其检测精度。
(4)本文方法可以在线检测平面度,配合水平定位在线控制装置,可以实现平面度的在线连续测量。
[参考文献]
[1]GB/T11337—2004,平面度误差检测[S].
[2] 陈宝刚,邵亮,李剑锋.大直径窄环带平面平面度的精确测量[J].光电工程,2015(8):14-19.
[3] 陈小宁,郭进,姚一永.基于双目视觉和投影圆的平面度非接触检测方法[J].四川兵工学报,2013,34(3):99-102.
[4]VMaurizio.Absoluteflatnessmeasurementusingobliqueincidencesetupandaniterativealgorithm.Ademonstrationonsyntheticdata[J].OpticsExpress,2014,22(22):3538-3546.
[5]LZhao,QOuyang,DChen,etal.StudyonCCDlaserscanningflatnessmeasurementmethodforhotrolledstrip[J].Ironmaking&Steelmaking, 2015,42(8):600-607.
[6] 段洁,孙向阳,蔡敬海,等.PSD在激光位移检测系统中的应用研究[J].红外与激光工程,2007,36(Z):281-284.
[7]RPorrazzo,LLydecker,SGattu,etal.Self-BalancingPosition-SensitiveDetector(SBPSD)[J].Sensors,2015,15(7):17483-17494.
[8] 尚鸿雁.二维PSD动态响应误差分析[J].红外与激光工程,2008,37(Z):302-305.
[9] 侯金龙.PSD激光三角测量系统的研制[D].武汉:华中科技大学,2005.
[10] 袁勃,张桂香,陈根余,等.基于CCD传感器的砂轮轮廓测量系统设计[J].传感器与微系统,2014,33(1):101-104.
[11] 沈磊,李顶根,褚俊,等.激光三角法位移测量中数字散斑相关法的研究[J].红外与激光工程,2014,43(1):288-293.
(编辑李秀敏)
文章编号:1001-2265(2016)07-0082-04
DOI:10.13462/j.cnki.mmtamt.2016.07.023
收稿日期:2016-01-18;修回日期:2016-02-26
*基金项目:国家自然科学基金(61571030)
作者简介:韩金玉(1978—),女,河北邢台人,天津中德职业技术学院讲师,硕士,研究方向为计算机视觉与智能化检测与监控研究,(E-mail)715549796@QQ.com。
中图分类号:TH741;TG506
文献标识码:A
Measuring Method of Departures from Flatness using Position Sensitive Detector
HAN Jin-yua,WANG Shou-zhib
(a.ElectricalEngineeringandEnergySchool;b.Aviation,AerospaceandAutomobileSchool,TianjinSino-GermanUniversityofAppliedSciences,Tianjin300350,China)
Abstract:In order to realize online detection of flatness error,a kind of flatness on-line Measuring method of applying the direct optical triangulation is proposed that is based on the analysis of flatness evaluation method of the least-square method and the principle of position sensitive detector, and an experimental device is designed.Firstly the measured surface of the Z axis deviation value is detected gradually by three groups of Position Sensitive Detector,the coordinate values of the measured point are determined,then the flatness is calculated with the least square method,and the flatness error value is calculated.The results of the simulation showed that the precision of the method in this paper for the general plane is high,which is better than that of micrometer indicator,and the measurement results are reliable and effective.
Key words:flatness; departures;position sensitive detector

