3DOF-PAM并联机器人设计与动力学建模*

薛帮灿,郝丽娜,杨　辉

(东北大学 机械工程与自动化学院，沈阳　110819)



3DOF-PAM并联机器人设计与动力学建模*

薛帮灿,郝丽娜,杨辉

(东北大学 机械工程与自动化学院，沈阳110819)

摘要：该设计依据气动肌肉特性和并联机器人理论，结合仿生学的设计方法，开发了一个3自由度气动肌肉并联机器人机构。基于气动肌肉的变刚度特性，将其简化为变刚度弹簧，并通过考虑其在机构运动过程中的质心变化特性，结合拉格朗日动力学方法对3DOF-PAM并联机器人进行动力学建模，运用MATLAB软件对建立的动力学模型进行仿真分析研究，分析3DOF-PAM并联机器人在不同负载下运动过程中的动力学特性，为气动肌肉驱动的并联机器人的高精度轨迹控制建立理论基础。

关键词：气动肌肉；并联机器人；结构设计；动力学建模

0引言

由于气动肌肉具有高功率密度比、良好的柔顺性及安全性、以及轻质、灵活等优点，故其在高功率密度比的驱动装置的设计开发中得到了广泛应用。例如美国华盛顿天主教大学研究了拮抗的气动肌肉手臂结构[1]，纳什维尔大学研制了6自由度的机械臂[2-3]，日本Bridgestone公司研制了5自由度的柔顺机械臂[4]等，但是对于采用气动肌肉并联驱动方式的机器人机构的研究相对较少。目前国外，新西兰奥克兰大学研制了一种四根气动肌肉驱动的三自由度柔性并联机器人用于脚踝康复[5]，韩国釜山东义大学研制了3DOF-PAM并联外骨骼式康复机器人[6]。国内，华中科技大学研究由3根PAM组成的非对称并联机器人平台[7]，北京理工大学研究了3DOF-PAM球面并联机器人[9]。

目前在建立PAM机械臂精准动力学模型方面，国内外均进行了一定的研究，例如文献[1]利用能量守恒和虚功原理建立气动肌肉静态模型，结合拉格朗日动力学方法建立气动肌肉手臂的动力学模型；文献[7]利用气动肌肉静态模型与牛顿-欧拉方法建立并联机器人动力学模型。由此可知，目前针对气动肌肉驱动的机器人装置的动力学建模，大多是从能量守恒原理或变截面气缸的角度来建立PAM静力学模型，并结合装置机构特点建立整个系统的动力学模型。

本文基于气动肌肉的变刚度特性，将其简化为变刚度弹簧，并通过考虑其在机构运动过程中的质心变化特性，根据拉格朗日方程建立3DOF-PAM并联机器人的动力学模型，并对其动力学特性进行仿真分析，从而为仿生肘关节的变刚度控制奠定理论基础。

13DOF-PAM并联机器人结构设计

根据身高168mm中国成年男子上臂尺寸以及并联机器人理论，设计基于气动肌肉驱动的并联机器人机构。其采用3自由度并联机构，由固定平台、运动平台、支撑杆、虎克铰、连接小轴及气动肌肉等组成，其中固定平台安有3个虎克铰、运动平台安有4个虎克铰，每个虎克铰通过连接小轴与对应平台相连；3根气动肌肉的两端分别通过虎克铰与固定平台及运动平台相连；支撑杆下端通过螺纹与固定平台固连，上端通过虎克铰与运动平台相连。分别对3根气动肌肉进行充放气，从而对运动平台位姿进行调整，实现运动平台的屈/伸、外展/内收以及旋内/旋外3个旋转自由度。根据外观图1，3DOF-PAM并联机器人的主要参数如表1所示，其设计指标如表2所示。

表1　气动肌肉并联机器人主要参数

表2　设计指标参数

图1　3DOF-PAM并联机器人

23DOF-PAM并联机器人动力学建模

2.1气动肌肉静态模型

文献[9]采用能量守恒原理和虚功原理，建立气动肌肉输出力与压力和长度之间的函数关系。其首先假设气动肌肉是壁厚为0的圆柱体，且其编织网拥有很低的延展性，气动肌肉的体积主要取决于编织网的长度，如图2所示。

图2　气动肌肉简图

图中：L—为圆柱体长度、θ—为编织网线与圆柱体轴之间的夹角、D—为圆柱体直径、n—为线缠绕匝数、b—为单根丝线的长度。其L=b·cosθ,D=b·sinθ/nπ,圆柱体体积为：

(1)

气动肌肉输出力F可表示为输入压强p′与编织角θ的函数，表达式如下：

(2)

对上述气动肌肉理想数学模型做进一步的数学变换，得到如下表达式：

(3)

式中：D0为气动肌肉初始直径、θ0为编织网的初始编织角、ε为气动肌肉收缩率。

2.2并联机器人动力学建模

根据拉格朗日法L=K-P,其中K为机械系统的动能，P为机械系统的势能。

(4)

将L=K-P代入(1)式中则有：

(5)

图3　3DOF-PAM并联机器人简化模型

3DOF-PAM并联机器人简化模型如图3所示，由于气动肌肉可以简化为变刚度弹簧，气动肌肉实际长度L与初始长度L0之差相当于弹簧的伸长量x。由3.1节中的气动肌肉的静态数学模型(3)式可求得气动肌肉的刚度k：

(6)

式中：x是气动肌肉的收缩量，x=L-L0。

ρ(y)=ms/l

(7)

气动肌肉上任意两点间的位置坐标间关系式为：

(8)

式中：αi为气动肌肉轴线与水平面的夹角，li为气动肌肉拉伸后的长度。

气动肌肉质心到端点的距离Lci为：

(9)

根据图3所示坐标系，机构的旋转矩阵为：

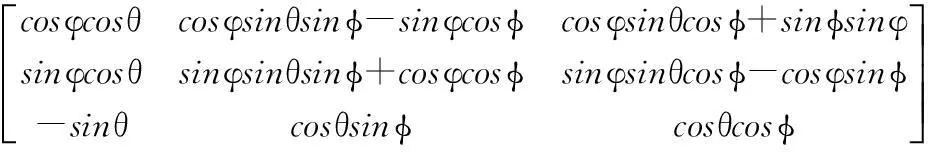
(10)

zpi′=BRmbi′m-BRmbim=

所以对上述表达式进行简化得：

(11)

设气动肌肉轴线与水平面的夹角为α；则夹角满足：

所以气动肌肉质心到端点的距离为：

(12)

各根气动肌肉总动能为：

综上，该机构的总动能为：

(13)

机构的总势能为平台势能与各杆的势能之和，其中气动肌肉的势能包括重力势能和弹性势能，则有：

(14)

结合(2)、(13)、(14)式，可得到动力学方程为：

(15)

33DOF-PAM并联机器人动力学仿真分析

对于3DOF-PAM并联机器人的动力学研究，主要是分析肘关节在不同的运动形式下，三根气动肌肉的驱动力变化情况。根据已建立的并联机器人动力学方程，针对并联机器人在不同的运动形式下，对三根气动肌肉的驱动力情况进行仿真实验研究，图4为并联机器人空载运动时各根气动肌肉驱动力变化情况，图5为并联机器人负重2.5kg条件下运动时各根气动肌肉驱动力变化情况，图6为负重5kg条件下运动时各根气动肌肉驱动力变化情况。输入转角分别为φ=50°sint、θ=50°sint。

图4　并联机器人空载动力学仿真结果

仿真结果分析：图4为3DOF-PAM并联机器人空载运动时，各根气动肌肉驱动力变化仿真结果。图4a中并联机器人的运动平台绕X轴转动时，由于第一根气动肌肉位于XOZ平面内，其长度没有发生变化，所以驱动力为恒定值；另外两根气动肌肉驱动力不断发生变化，且为一大一小，原因为运动平台转动过程中，两根肌肉的收缩量变化不同。在运动平台转到最大转角位置，气动肌肉驱动力最大为277N。图4b为并联机器人的运动平台绕Y轴转动，运动平台质心靠近L2、L3两根气动肌肉，在平台转动到极值位置，L2、L3驱动力也较第一根气动肌肉大，主要由其承受运动平台自身负载。

图5　肘关节带载2.5kg动力学仿真结果

图5为并联机器人运动平台带载2.5kg时，各根气动肌肉驱动力变化仿真结果。从图5a可以看出在负重2.5kg情况下，运动平台达到最大转角时，L2和L3两根气动肌肉驱动力达到380N，较空载运动时驱动力增大了103N。图5b中当运动平台达到最大转角处，出现L2和L3驱动力变化显著大于L1的驱动力值，主要因为运动平台质心位置靠近L2和L3，运动平台到达靠近L2和L3位置的最大转角处，负载主要由这两根气动肌肉承担，收缩量也增大，故驱动力增大，并且驱动力值接近500N。

图6　肘关节带载5kg动力学仿真结果

图6为并联机器人的运动平台带载5kg时，各根气动肌肉受力变化仿真结果。图6a相比图5a可知，在平台运动过程中，各根气动肌肉驱动力的变化趋势没有改变，但在运动平台达到最大转角位置处，气动肌肉驱动力显著增加，增加值近170N。从图6b中可以看出，当运动平台达到最大转角时，气动肌肉驱动力已经超过其极限载荷值750N，故该3DOF-PAM并联机器人所能承受最大负载不能超过5kg。

4结论

(1)本文基于气动肌肉的变刚度特性，将其简化为变刚度弹簧，通过考虑其在机构运动过程中的质心变化特性，并结合拉格朗日动力学方法建立了3DOF-PAM并联机器人的动力学模型。

(2)运用MATLAB软件仿真分析了并联机器人在所设计的转角指标范围内运动时，各根气动肌肉的受力变化情况。从仿真结果可知运动平台空载和带载两种情况下运动，气动肌肉驱动力的变化趋势有所不同；带载时，在不同负载条件下，3根气动肌肉各自驱动力的变化趋势不变，但随着负载的增加，其最大驱动力均有不同程度的增大。根据仿真结果可以看出并联机器人所能承受最大负载不超过5kg。

通过动力学模型的建立与仿真分析，为3DOF-PAM并联机器人的高精度轨迹控制以及人工肌肉机械臂的研发建立了理论基础。

[参考文献]

[1]ColbrunnRW,NelsonGM,QuinnRD.Designandcontrolofaroboticlegwithbraidedpneumaticactuators[C].IntelligentRobotsandSystems,2001.Proceedings.2001IEEE/RSJInternationalConferenceon.IEEE,2001,2:992-998.

[2]KawamuraK,BagchiS,ArousM,etal.Intelligentroboticsystemsinserviceofthedisabled[J].RehabilitationEngineering,IEEETransactionson,1995,3(1):14-21.

[3]AAlford,SNorthrup,KKawamura,etal.Amusicplayingrobot[C].Proc.oftheConf.onFieldandServiceRobots.1999:29-31.

[4]KanjiInoue.Rubbertuatorsandapplicationsforrobots[C].Proceedingsofthe4thinternationalsymposiumonRoboticsResearch.MITPress,1988:57-63.

[5]PrashantKumarJamwal,etal.Kinematicdesignoptimizationofaparallelanklerehabilitationrobotusingmodifiedgeneticalgorithm[J].RoboticsandAutonomousSystems,2009,57(10):1018-1027.

[6]Young-minKim,Sung-yoonJung,InhyukMoon.Designofawearableupper-limbrehabilitationrobotusingparallelmechanism[C].ICCAS-SICE,2009.IEEE,2009:785-789.

[7] 杨钢, 李宝仁,傅晓云.气动人工肌肉并联机器人平台[J].机械工程学报,2006,42(7):39-45.

[8] 范伟,彭光正,高建英,等.气动人工肌肉驱动三自由度球面并联机器人关节的位置控制研究[J].液压气动与密封,2003(6):1-5.

[9]CPChou,BHannaford.StaticandDynamicCharacteristicsofMcKibbenPneumaticArtificialMuscles[C].Proceedingsof1994IEEEInternationalConferenceonRoboticandAutomation.SanDiego,USA.1994,1:281-286.

[10]LeDuyKhoa,DinhQuangTruong,KyoungKwanAhn.Synchronizationcontrollerfora3-Rplanarparallelpneumaticartificialmuscle(PAM)robotusingmodifedANFISalgorithm[J].Mechatronics,2013,23:462-479.

[11]RASIMS，ALIZADEI.Forwardandreversedisplacementanalysisofa6-DOFin-parallelmanipulators[J].InternationalJournalofTools&Manufacture，1997，39(2):321-342.

[12] 余跃庆，徐齐平.柔顺机构PR伪刚体动力学建模与特性分析[J].农业机械学报，2013，44(3)：225-229.

[13] 韩方元，赵丁选，李天宇.3-RPS并联机构正解快速数值算法[J].农业机械学报，2011，42(4)：229-233.

[14] 王南，赵乘康，高鹏，等.并联机构3-SPS/S的静、动态刚度性能研究[J].机械设计与制造，2013(8)：213-215.

(编辑李秀敏)

文章编号：1001-2265(2016)07-0052-04

DOI:10.13462/j.cnki.mmtamt.2016.07.015

收稿日期：2015-08-13；修回日期：2015-09-10

*基金项目：国家高技术研究发展计划(863计划)(2015AA042302)；装备预先研究项目(62501040412)；辽宁重大装备制造协同创新中心资助

作者简介：薛帮灿(1990—)，男，河南周口人，东北大学硕士研究生，研究方向为气动肌肉仿人机械臂的研究；通讯作者：郝丽娜(1968—)，女，辽宁庄河人，东北大学教授，博士生导师，研究方向是机器人系统与智能控制，(E-mail)haolina@me.neu.edu.cn。

中图分类号：TH166;TG506

文献标识码：A

Design and Dynamic Modeling of 3DOF-PAM Parallel Robot

XUE Bang-can,HAO Li-na,YANG Hui

(SchoolofMechanicalEngineering&Automation，NortheasternUniversity，Shenyang110819,China)

Abstract：According to the pneumatic muscle characteristics and parallel robot theory,combined with bionics design method,a 3DOF-PAM parallel robot was designed. Based on the change of stiffness of pneumatic muscle, it is simplified as a variable stiffness spring,and the change of centroid of PAM during motion of mechanism is considered.Dynamics model of 3DOF-PAM parallel robot was established by using the Lagrange dynamics method. MATLAB software was employed to conduct simulation experiments of the dynamics model, and dynamics characteristic of 3DOF-PAM parallel robot was studied in the movement process of different load.The foundation of the high precision trajectory control of parallel robot driven by PAM was established.

Key words：pneumatic muscle;parallel robot;architectural design;dynamics modeling